压制二元组的总价值
压制二元组的总价值
对于每一个 a i a_i ai, 看它能压制它前面的多少个元素, 那么它对总价值的贡献就是:
在a数组中:
- a i a_i ai压制了x个数, 贡献为: x ∗ i x*i x∗i
- 被 a i a_i ai所压制的所有数在 a a a中的下标和为 y y y, 贡献为 − y -y −y
树状数组来求:
- 为了快速求出 a i a_i ai压制了几个数, 记录 a i a_i ai前面的所有数在 b b b中的下标 m a p ( a [ i ] ) map(a[i]) map(a[i]),值 t r b [ m a p ( a [ i ] ) ] = 1 trb[map(a[i])]=1 trb[map(a[i])]=1表示它出现过,
这样每次只需通过 s u m ( m a p [ a [ i ] ] ) sum(map[a[i]]) sum(map[a[i]])即可得出它前面已经出现了多少个数.
- 记录 a i a_i ai前面的所有数在b中的下标 m a p ( a [ i ] ) map(a[i]) map(a[i]), 值 t r a [ m a p ( a [ i ] ) ] tra[map(a[i])] tra[map(a[i])]为它在 a a a中的下标 i i i, 每次 s u m sum sum即可得出它所压制的所有数的下标和.
import java.io.*;
import java.util.*;public class Main {static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));static StreamTokenizer stmInput = new StreamTokenizer(br);static int N = 200010;static long tra[] = new long[N], trb[] = new long[N];static int a[] = new int[N], b[] = new int[N];static HashMap<Integer, Integer> map = new HashMap<>();static int n;public static int readInt() throws IOException {stmInput.nextToken();return (int) stmInput.nval;}public static int lowbit(int x){return x & -x;}public static void add(int x, int c, long tr[]){for (int i = x; i <= n; i += lowbit(i)) {tr[i] += c;}}public static long sum(int x, long tr[]){long res = 0;for (int i = x; i >= 1; i -= lowbit(i)) {res += tr[i];}return res;}public static void solve() throws IOException{n = readInt();for (int i = 1; i <= n; i++) {a[i] = readInt();}for (int i = 1; i <= n; i++) {b[i] = readInt();map.put(b[i], i);}long ans = 0;for (int i = 1; i <= n; i++) {// 1.ai压制了多少个数ans += i * sum(map.get(a[i]), tra);add(map.get(a[i]), 1, tra);// 2.被ai压制的所有数在a中的下标和ans -= sum(map.get(a[i]), trb);add(map.get(a[i]), i, trb);}pw.println(ans);}public static void main(String[] args) throws IOException {int T = 1;while(T-- != 0){solve();}pw.flush();pw.close();br.close();}}
相关文章:

压制二元组的总价值
压制二元组的总价值 对于每一个 a i a_i ai, 看它能压制它前面的多少个元素, 那么它对总价值的贡献就是: 在a数组中: a i a_i ai压制了x个数, 贡献为: x ∗ i x*i x∗i被 a i a_i ai所压制的所有数在 a a a中的下标和为 y y y, 贡献为 − y -y −y 树状数组来求: 为了…...

【习题】保存应用数据
判断题 1. 首选项是关系型数据库。 错误(False) 2. 应用中涉及到Student信息,如包含姓名,性别,年龄,身高等信息可以用首选项来存储。 错误(False) 3. 同一应用或进程中每个文件仅存在一个Preferences实例。 正确(True) 单选题 …...
Flask框架小程序后端分离开发学习笔记《5》简易服务器代码
Flask框架小程序后端分离开发学习笔记《5》 Flask是使用python的后端,由于小程序需要后端开发,遂学习一下后端开发。 简易服务器代码 接口解析那一块很关键,学后端服务器这一块,感觉主要就是学习相应地址的接口怎么处理。 然后…...

“计算机视觉处理设计开发工程师”专项培训(第二期)
“人工智能技术与咨询” 发布...
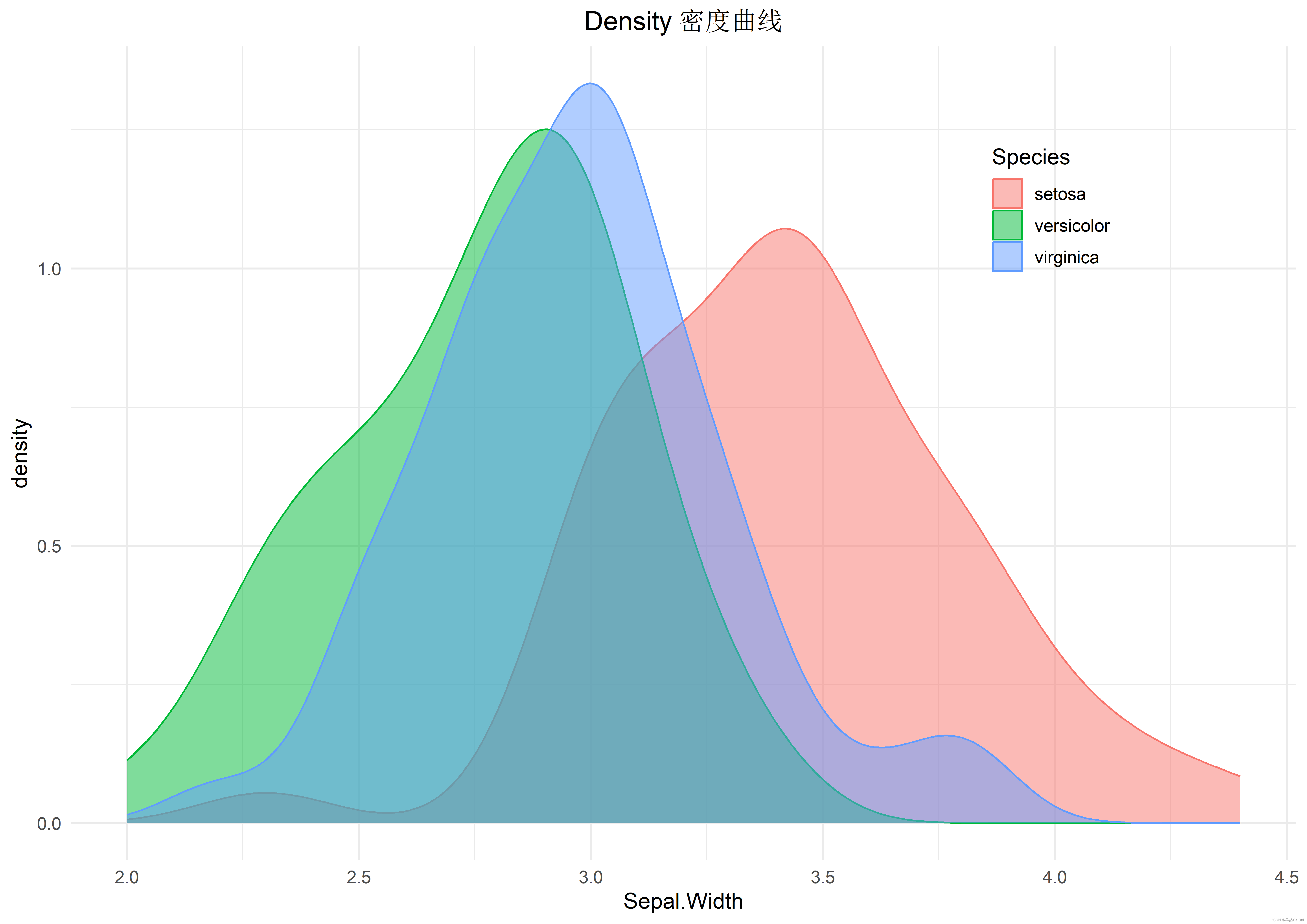
R语言学习case7:ggplot基础画图(核密度图)
step1: 导入ggplot2库文件 library(ggplot2)step2:带入自带的iris数据集 iris <- datasets::irisstep3:查看数据信息 dim(iris)维度为 [150,5] head(iris)查看数据前6行的信息 step4:画图展示 plot2 <- ggplot(iris,aes(Sepal.W…...

Ubuntu18配置Docker
1.基本过程 1.更新软件源列表 sudo apt update2.安装软件包依赖 sudo apt install apt-transport-https ca-certificates curl software-properties-common3.在系统中添加Docker的官方密钥 curl -fsSL https://download.docker.com/linux/ubuntu/gpg | sudo apt-key add - …...

Keil/MDK平台 - 结构体成员指针注意事项
文章目录 1 . 前言总结2 . 问题现象3 . 解决思路4 . 细节扩展5 . 总结 【极客技术传送门】 : https://blog.csdn.net/Engineer_LU/article/details/135149485 1 . 前言总结 有时候希望通过类定义的类型指向数据包来解析,恰好又想结构体内定义指针指向一段数据&…...
一款超级好用的远程控制APP,你值得拥有
在这个科技日新月异的时代,我们的生活被各种手机软件所包围。几乎每个人都有一个甚至多个手机,你是否也有遇到过需要远程操作自己某一台手机的场景呢?今天,我要向大家推荐一款神奇的手机远程操作神器,让你可以随时随地…...

NumPy必知必会50例 | 18. 使用 NumPy 解决线性方程组:数学问题的实用解决方案
继续我们的 NumPy 探索之旅吧,接下来我们将探讨使用 NumPy 解决线性方程组,一种实用的数学应用。 文章目录 18. 使用 NumPy 解决线性方程组:数学问题的实用解决方案线性方程组:数学世界的基石创建线性方程组 解决实际问题应用场景…...
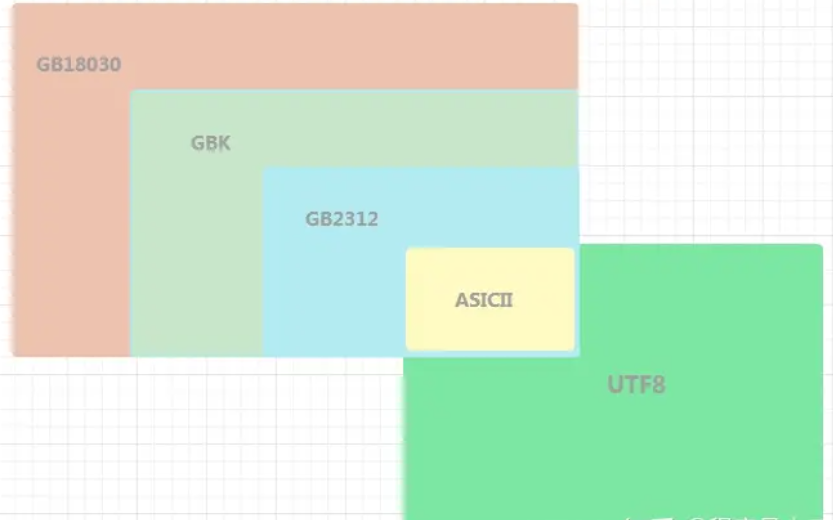
C/C++编码问题研究
文章目录 一、Unicode字符集与U8/U16/U32编码二、编码1. 占字节数2. ASCII、GB2312、GBK、GB18030 以及 UTF8 的关系3. BOM4. UTF-8的存储实现 三、编译器字符集设置1. GCC语法Example 2. MSVC语法Example 三、wchar_t五、编码转换函数六、代码 & 实践1. UTF8与UTF16、UTF3…...

二刷代码随想录|Java版|回溯算法3|子集问题
习题 2.3 子集问题 就是组合过程收集path。就像是代码随想录里说得那样,组合和分割问题就是收集叶子结点,子集问题就是收集每一个节点。 有涉及到同层重复元素的问题。 先排序,后再for循环里处理相同数值跳过。 设置函数内的used。 还可以用…...

mongodb config
windows: 1.同级bin,data,log创建mongo.config文件 dbpathD:\Program\mongodb\data\db logpathD:\Program\mongodb\log\mongo.log logappendtrue #默认启用日志 journaltrue #过滤无用日志信息,调试设置为false quiettrue port2…...

pytorch 实现中文文本分类
🍨 本文为[🔗365天深度学习训练营学习记录博客🍦 参考文章:365天深度学习训练营🍖 原作者:[K同学啊 | 接辅导、项目定制]\n🚀 文章来源:[K同学的学习圈子](https://www.yuque.com/mi…...
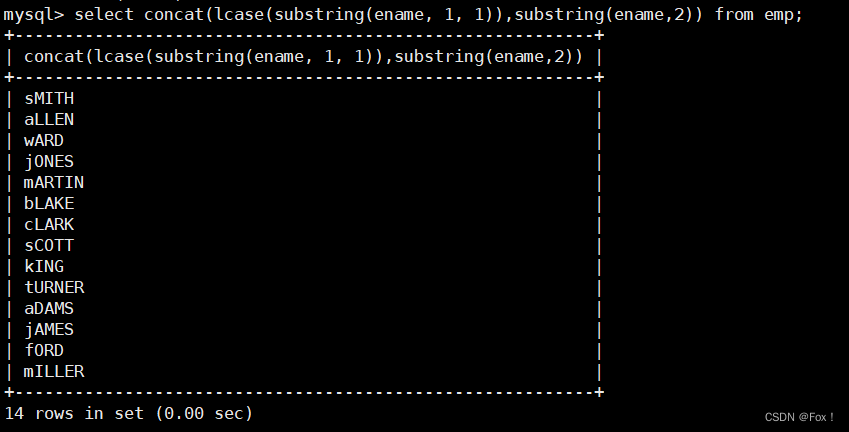
【MySQL】聚合函数和内置函数
文章目录 1 :peach:聚合函数:peach:2 :peach:group by子句的使用:peach:3 :peach:内置函数:peach:3.1 :apple:日期函数:apple:3.2 :apple:字符串函数:apple:3.3 :apple:数学函数:apple: 4 :peach:其它函数:peach: 1 🍑聚合函数🍑 函数说明COUNT([DISTIN…...
)
python第五节:集合set(4)
集合其他方法: len(s) set 的长度 x in s x 是否是 s 的成员 x not in s x 是否不是 s 的成员 s.issubset(t) 是否 s 中的每一个元素都在 t 中 s.issuperset(t) 是否 t 中的每一个元素都在 s s.union(t) 返回一个新的 set 包含 s 和 t 中的每一个元素 …...
———什么是okhttp?)
知识笔记(一百)———什么是okhttp?
OkHttp简介: OkHttp 是一个开源的、高效的 HTTP 客户端库,由 Square 公司开发和维护。它为 Android 和 Java 应用程序提供了简单、强大、灵活的 HTTP 请求和响应的处理方式。OkHttp 的设计目标是使网络请求变得更加简单、快速、高效,并且支持…...
Electron桌面应用实战:Element UI 导航栏橙色轮廓之谜与Bootstrap样式冲突解决方案
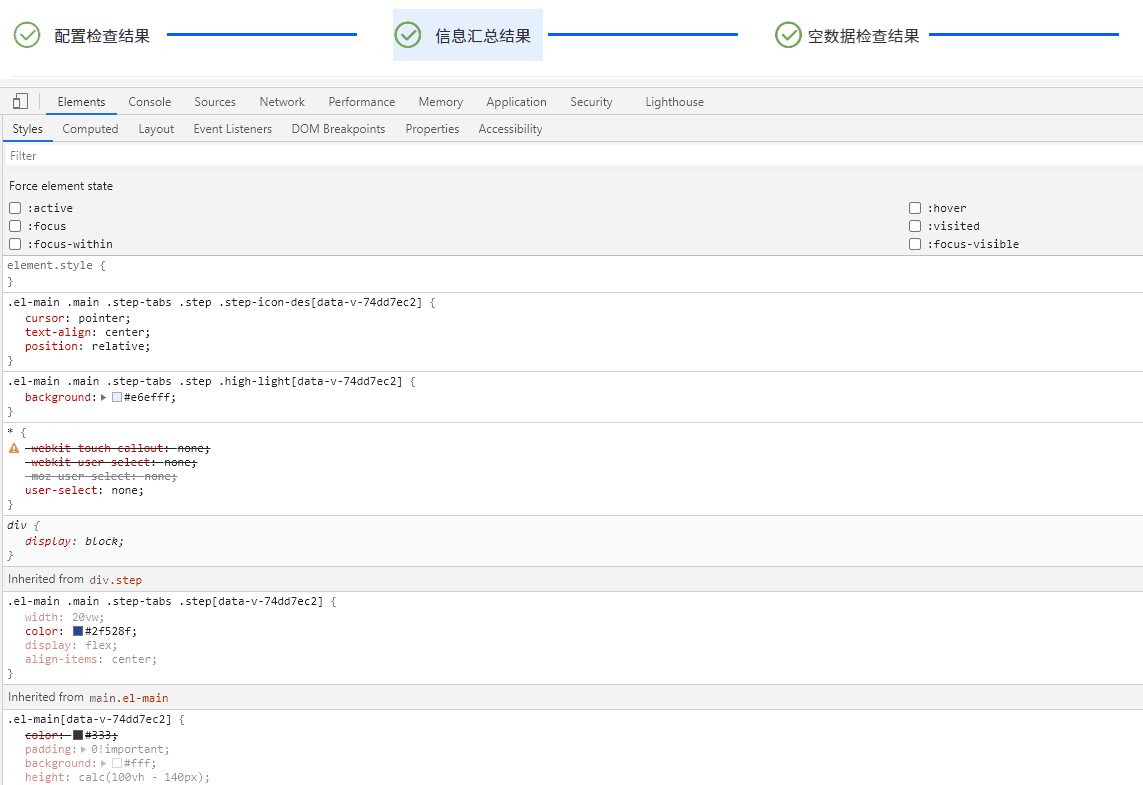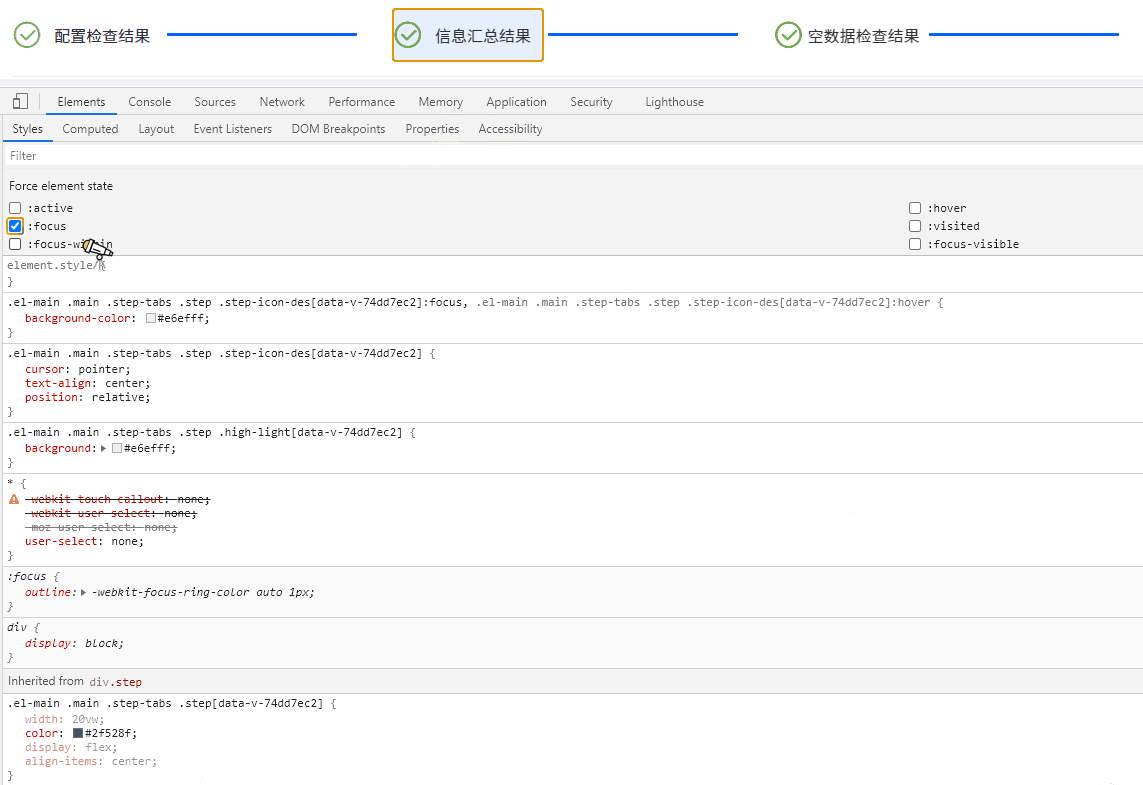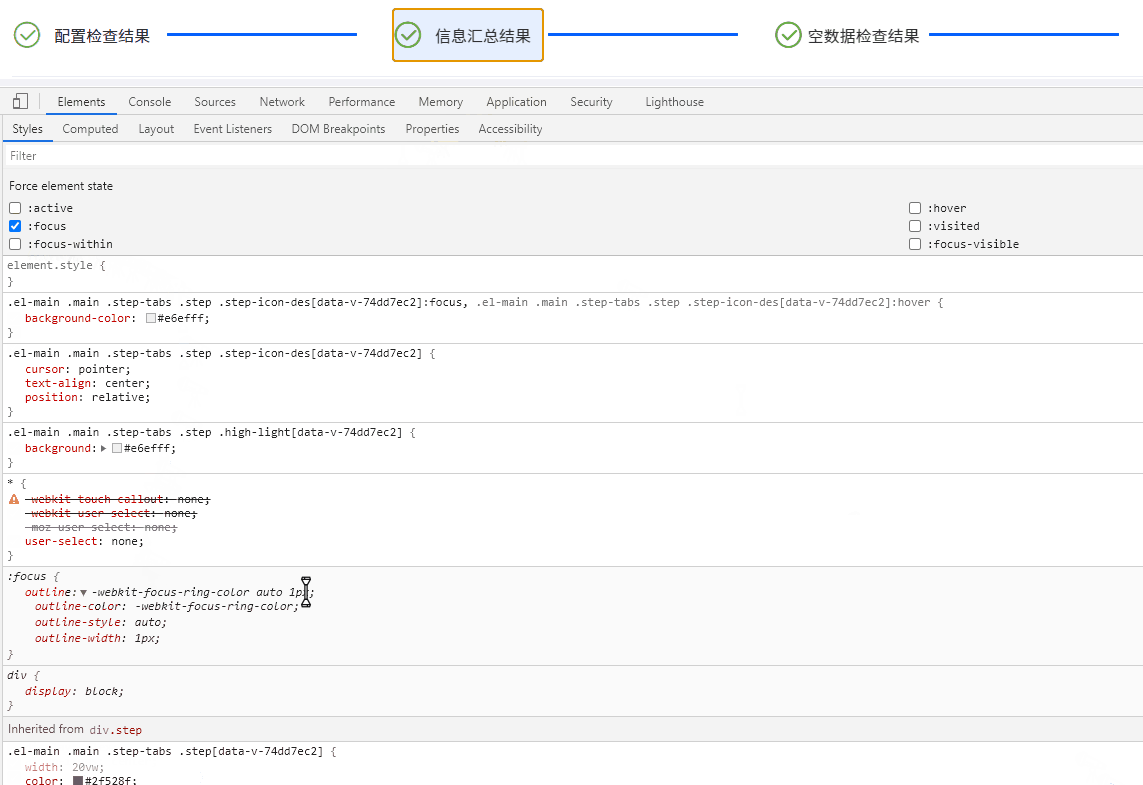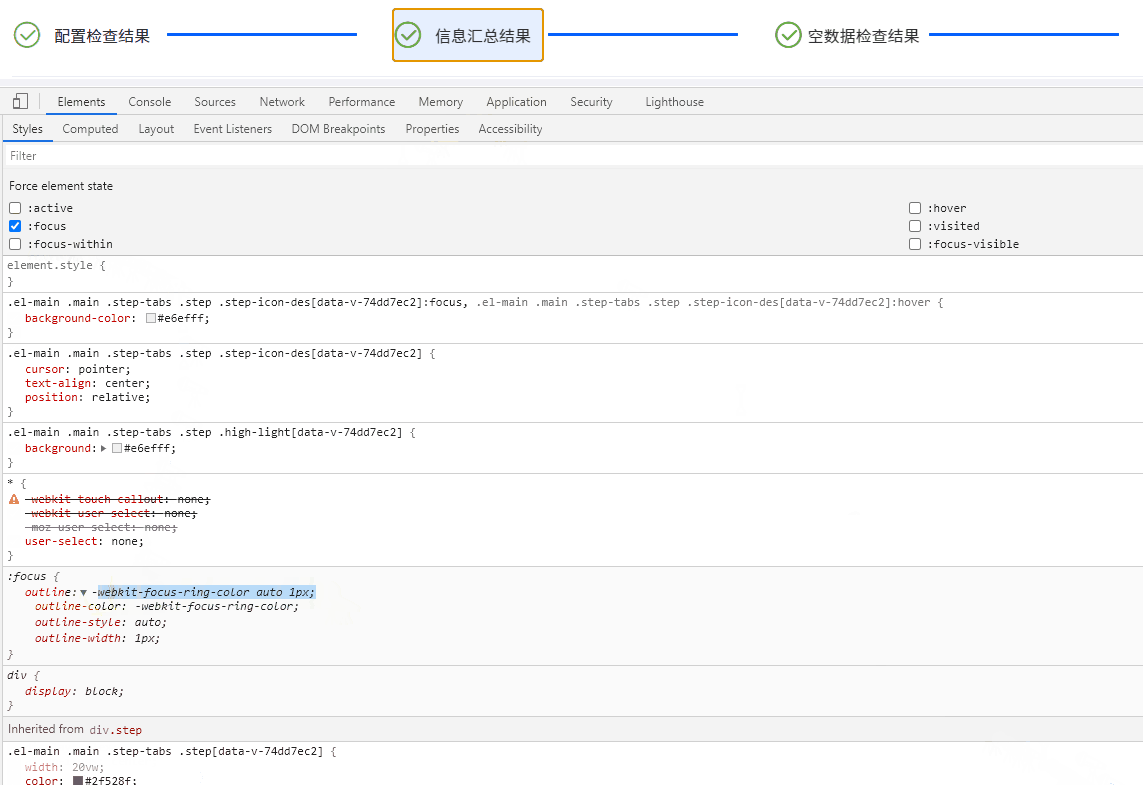
目录 引言 问题现象及排查过程 描述问题 深入探索 查明原因 解决方案与策略探讨 重写样式 禁用 Bootstrap 样式片段 深度定制 Element UI 组件 隔离样式作用域 结语 引言 在基于 Electron 开发桌面应用的过程中,我们可能时常遇到各种意想不到的问题…...
Nuget包缓存存放位置迁移
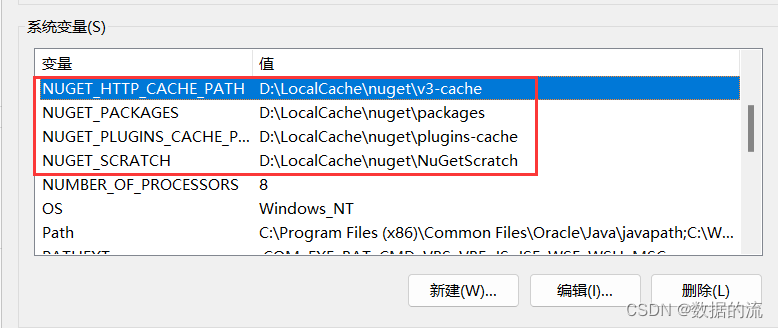
一、背景 默认情况下,NuGet会将项目中使用的包缓存到C盘,随着项目开发积累nuget包越来越多,这会逐渐挤占大量C盘空间,所以我们可以将nuget包缓存位置指定到其他盘中存放。 二、软件环境 win10、vs2022 三、查看当前缓存存放位…...
键盘上Ins键的作用
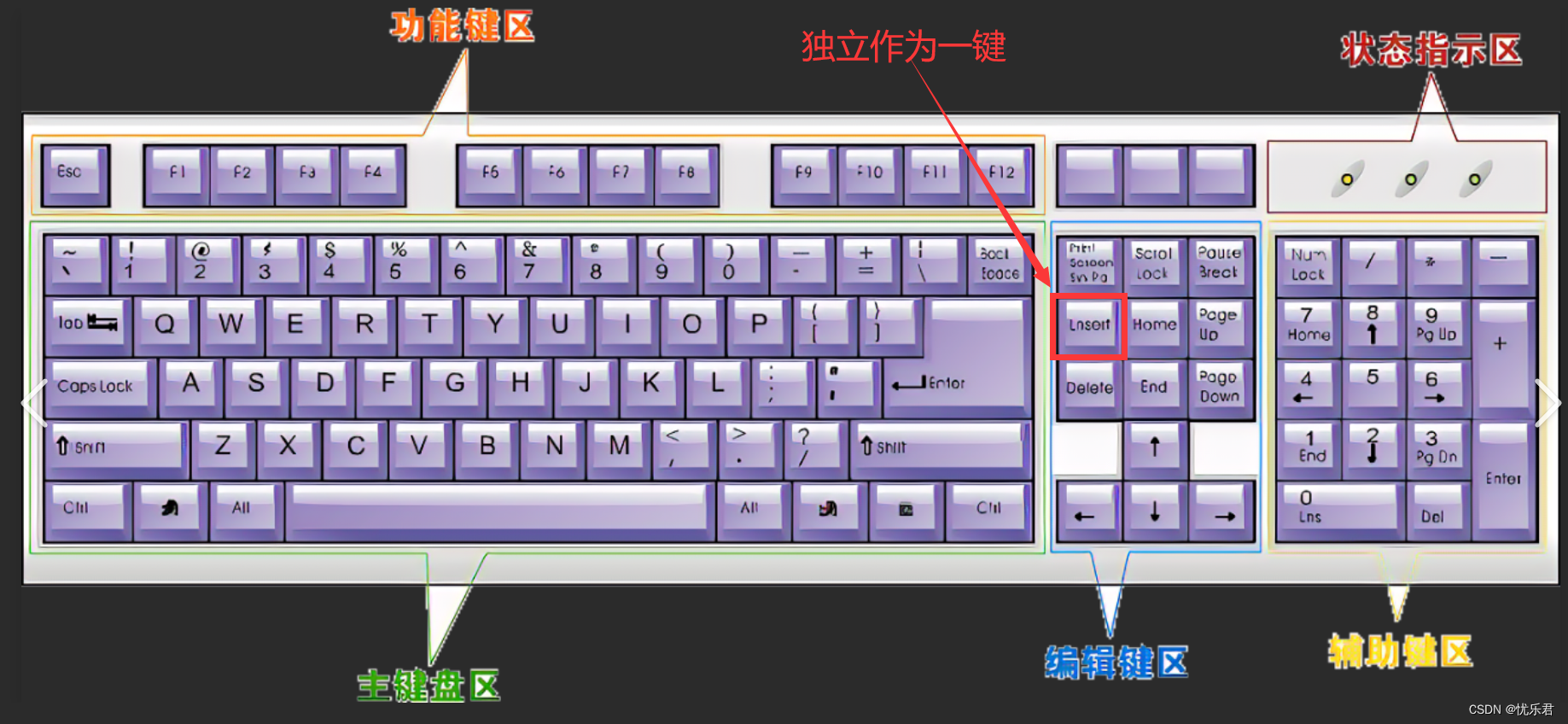
前几天编写文档时,发现一个问题:插入内容时,输入的字符将会覆盖光标位置后的字符。原来是按到了键盘上的 Ins键,解决方法是:再按一次 Ins键(Ins键如果独立作为一键时,否则使用 “Fn Ins”组合键…...

css display 左右对齐 技巧
.list_number{ display: flex; } .list_name_number{ width:100px; } //左边固定width .list_name_type{ //右边给flex:2 自动撑开 flex:2; }...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...
