【C深度解剖】计算机数据下载和删除原理
简介:本系列博客为C深度解剖系列内容,以某个点为中心进行相关详细拓展
适宜人群:已大体了解C语法同学
作者留言:本博客相关内容如需转载请注明出处,本人学疏才浅,难免存在些许错误,望留言指正
作者博客链接:睡觉待开机
下面是本节博客的大纲梳理:
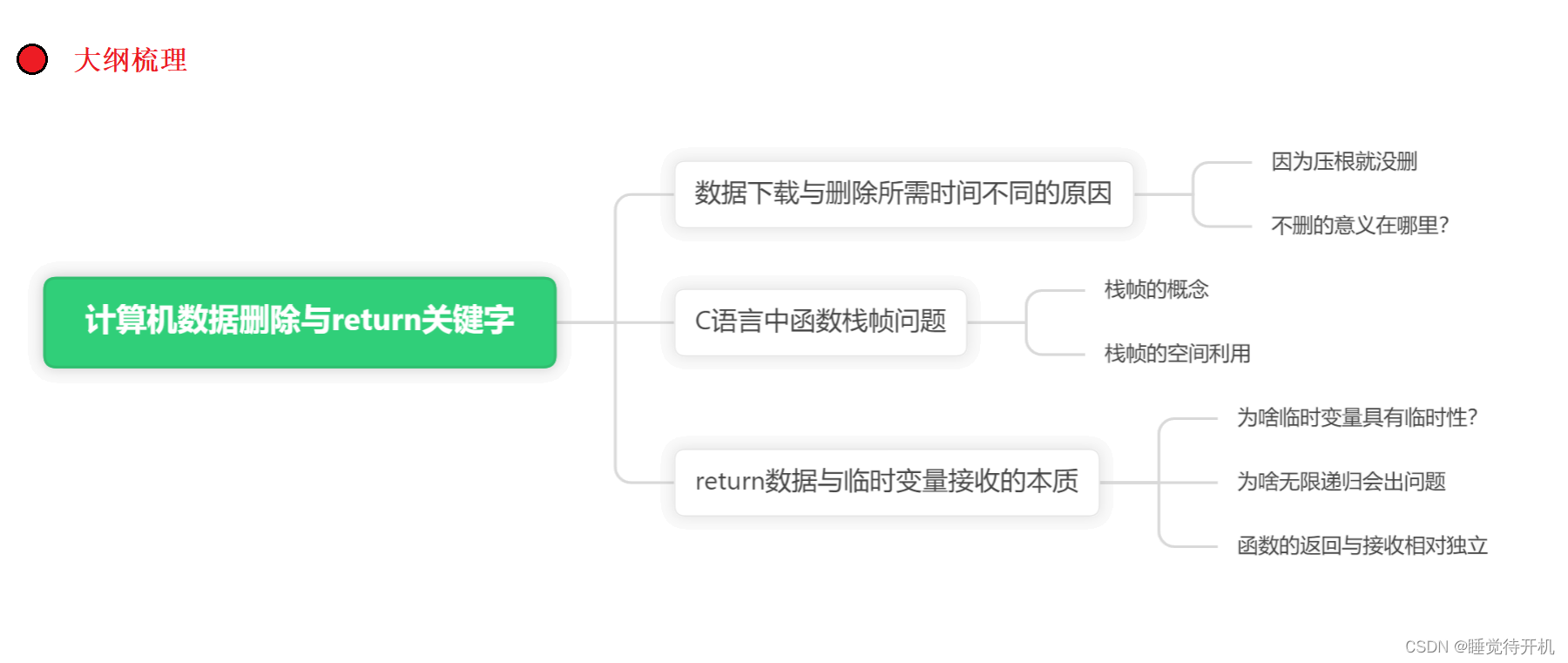
引言
在生活中,我需要下载一个视频或者软件时候,往往需要较长的时间(相对来说),但是我们如果删除相应的>视频或者软件时候,反而会很快(相对来说),这是为什么呢?
这是一个比较奇特的现象,(在不懂的人看来)。
下面针对该问题进行探讨,为了便于大家理解,我直接回答相关问题,最后再做示例演示。
正文
答案:计算机的数据下载,需要把大量二进制数据进行拷贝。而计算机的数据删除,本质上设置该数据无效即可,无需清空数据。
1.数据下载与删除所需时间不同的原因:
计算机数据的存入,需要把相应数据全部复制到存储硬件(内存、硬盘)中进行存储,也就是需要把该视频的音频数据,图像数据的所有二进制文件全部拷贝到计算机中,虽然计算机的处理速度很快,但是一个大一点的电影就是十几个G,再快也得几分钟才可以搞定。但是对于计算机而言,删除数据并不会像我们想象那样,需要把该视频文件全部回归初始状态,而是计算机直接宣布放该视频的这块内存空间允许被其他内容覆盖。明白了这些,自然数据下载很慢,而数据删除很快了,因为压根就没删。
为了便于大家理解,我做一个比喻:计算机的数据下载类似于我们盖一个新的大楼,说起盖大楼要先打地基,再向上一步一步搞,总之非常麻烦。但是,如果要拆除一座大楼呢?写个拆字就行了。当然与之不同的是大楼拆除是会破坏原来大楼的结构的,但是计算机为了效率的原因直接让那庞大的数据在那里就可以了,便不再管了,直到这块空间再次被使用,才会覆盖为新的内容。
那这里其实大家就可以联想到为什么有些人建议不要卖掉你的手机或者电脑,原因嘛,上面的说明就是一个大概的一个情况,具体这方面数据删除很复杂,明白上面所说即可。
但是可能有人就想问了,为啥计算机不把我们需要删除的内容进行修改防止个人信息泄露呢?
一是为了效率问题:如果要对删除内存空间进行初始化修改,计算机估计要多一倍的工作量,计算机是十分看重效率的,这么做我想设计者也是为了追求效率吧。
二是为了减少计算机本身的硬件损耗:这其实是硬件层面的知识了,我也不太清楚,只能说如果计算机对内存操作越频繁,那么存储硬件损耗会越快,我想这么做也是为了硬件寿命考量吧。
2.C语言中函数栈帧问题:
了解到上面所讲的计算机对数据的下载和删除原理之后,那么就可以联系到我们C语言中的函数栈帧了。我们知道我们C语言是由函数所构成的,那么函数是在哪里进行存储的呢?是在内存,在具体而言是在内存栈空间。
这里就不得不提一下C程序地址空间的相关概念了,这个C程序地址空间实际并不存在,是为了便于我们理解人们所抽象出来的操作系统进程地址空间,不是真正意义上的内存空间(不是内存真正的空间!)。
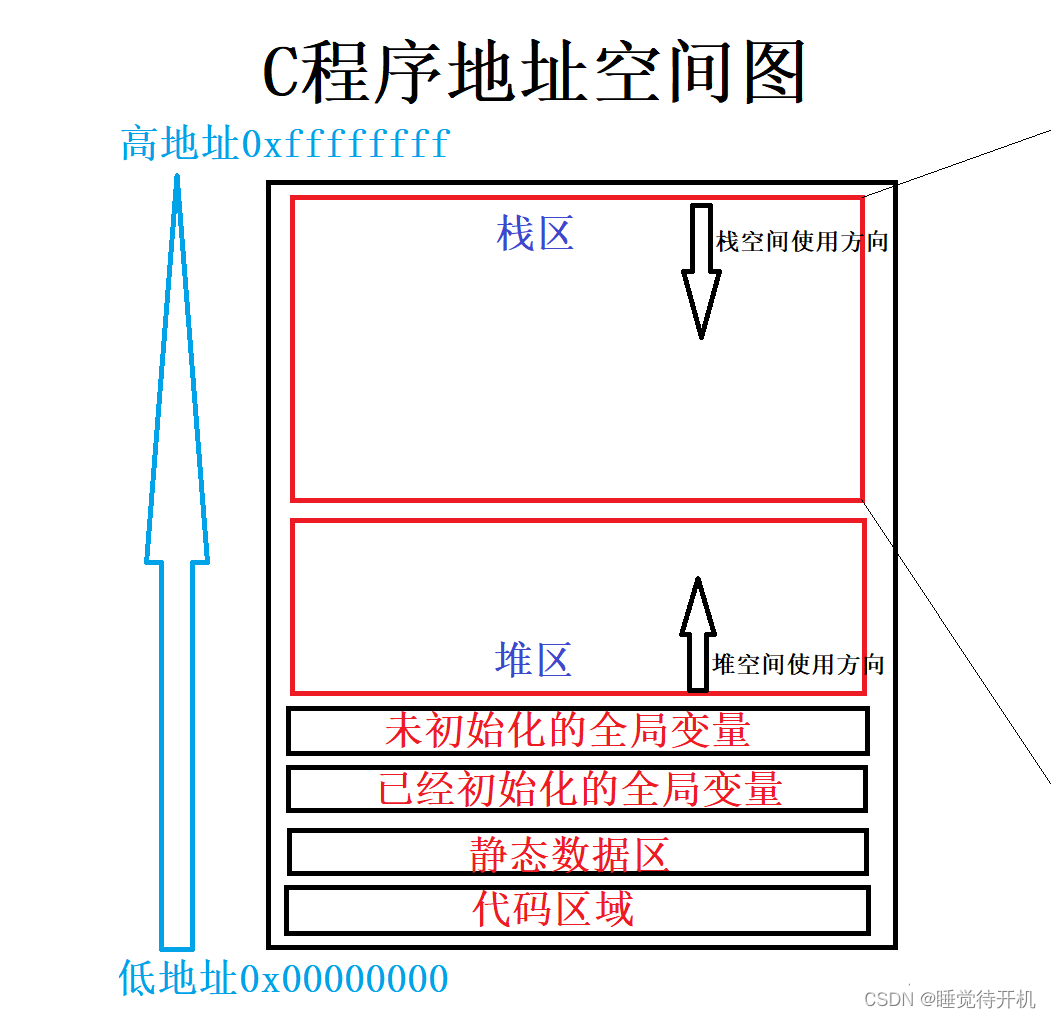
每当我们C程序调用一个函数时候,会预先给这个函数一块固定大小的空间,让该函数中的变量在所给该函数的栈空间中开辟属于变量的内存空间。在函数调用开始时候操作系统会把我们计算机内存中的一块空间给我们某个函数使用,一旦该函数调用结束,那么就收回该空间。
我们一般称操作系统给函数的这块空间为栈帧。
有同学可能好奇,为啥计算机知道要给这个函数分配多少空间啊?我可以比较形象的解释一下这个问题,因为计算机提前看了一眼你写的代码,虽然没有执行,但是大概知道你写的函数需要给多少空间啦。
总结下来就是,调用函数,形成栈帧,结束函数,释放栈帧,同理,这里释放栈帧只是允许其他内容覆盖该栈帧空间,并不是真正意义上的删除原先数据。
那么,实际上上面所说的内容,可以回答两个问题:
一是为啥局部变量具有临时性的问题:原因很简单,因为局部变量都是在函数内部进行定义的,也就是说变量的存在依托于他所在函数的存在,他函数所在空间都被收回了,作为在里面的变量自然也就消失了。
为了大家理解,我可以举个比喻性的例子,就是古代西方国家与贵族的例子吧,一个古代西方国家有一个国王还有一堆贵族组成,函数在这里就类似于国家,变量类似于贵族,你说国家都灭亡了,这个国家的贵族还能有吗?哈哈,对吧。这恰到好处的解释了为什么局部变量具有临时性的问题,你可能会疑问,那全局变量呢?全局变量的空间开辟并不是在函数内完成,而是跑到了全局数据区,伴随着程序的消亡而消亡,这又是另一个话题了。
二可以回答函数无限递归导致崩溃的问题:也很好理解,函数无限递归,也就是说在第一个函数里调用第二个函数,第二个函数里调用第三个函数…,一直调用,我们操作系统一直没有机会去收回我们函数的空间,栈空间迟早有一天会被无限递归占满,那么自然会导致栈溢出崩溃。
3.return数据与临时变量接收的本质
在C语言中,有一个关键字叫return,专门用来返回一个函数的返回值。我们说了,一个函数调用结束便意味着消亡,那么这个函数内的值是怎么返回到调用这个函数的函数中去的?
为了便于大家理解我说的啥意思,我直接给一个具体的例子:
//如何正确理解这段代码
#include <stdio.h>
#include <windows.h>
char* show()
{
char str[] = "hello bit";
return str;
}
int main()
{
char *s = show();
printf("%s\n", s);
system("pause");
return 0;
}
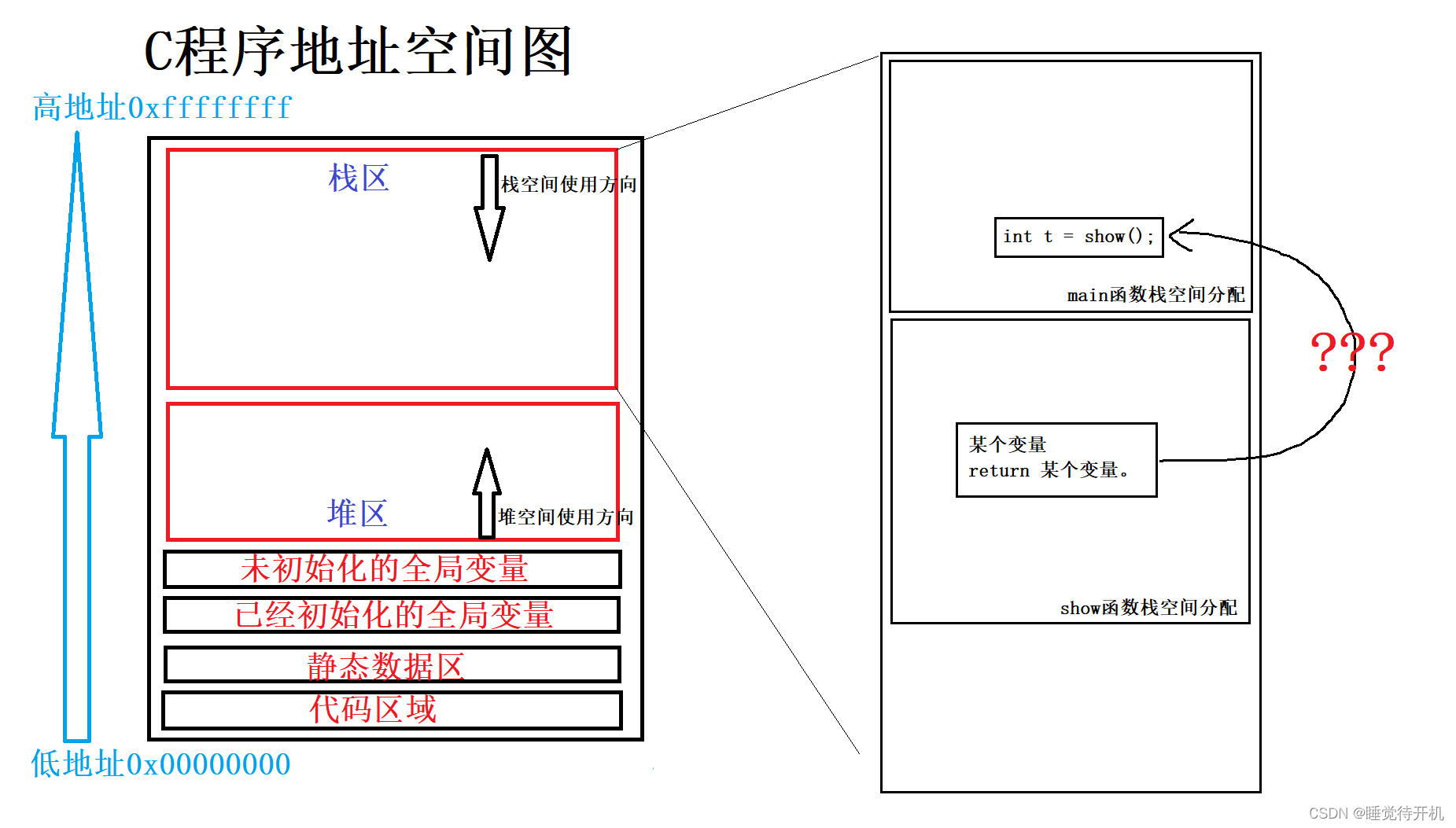
实际上,是借助了寄存器。
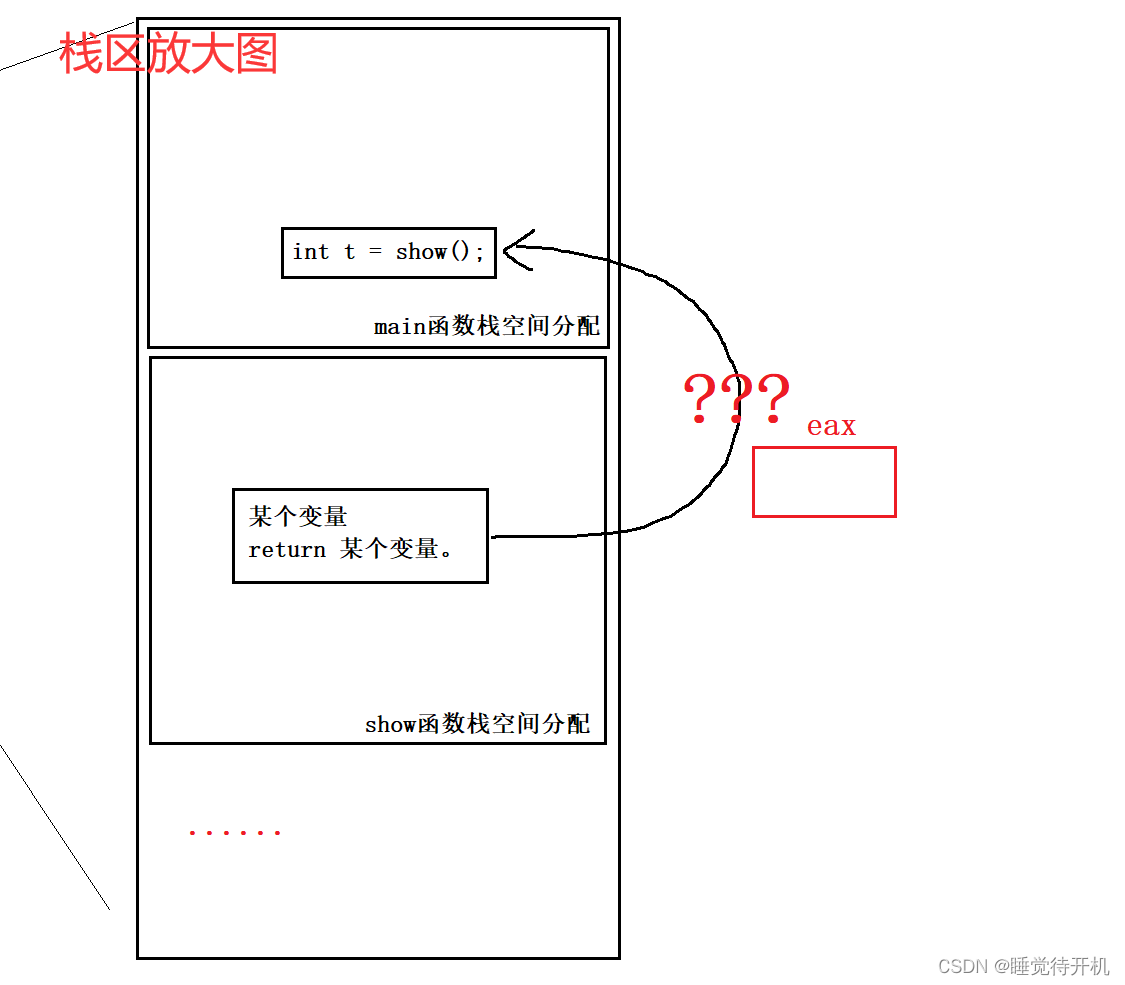
那么该如何验证呢?需要看反汇编。

上面代码的结果是:函数及时被销毁了,但是如果数据没有被覆盖那么依然可以找到数据,但是如果被覆盖了,那显示结果大概就是乱码了。
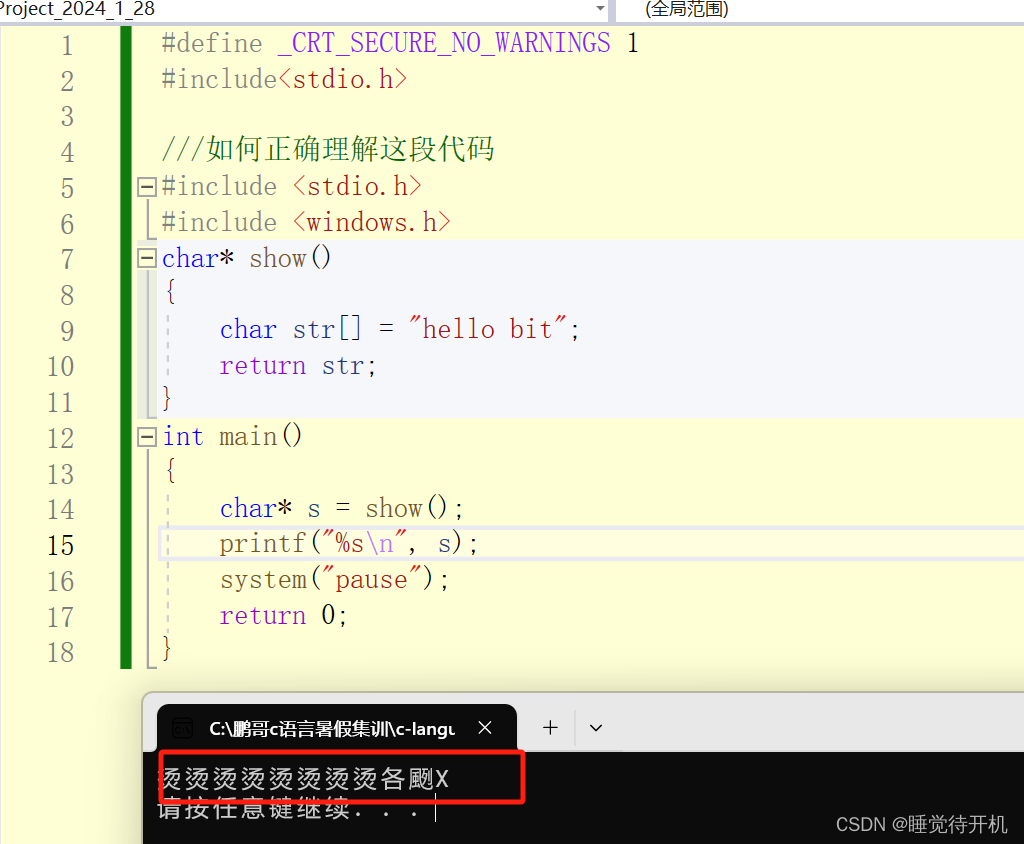
在这个例子中,覆盖show函数数据的函数是printf函数。
未覆盖数据之前,还可以看到原本的值:
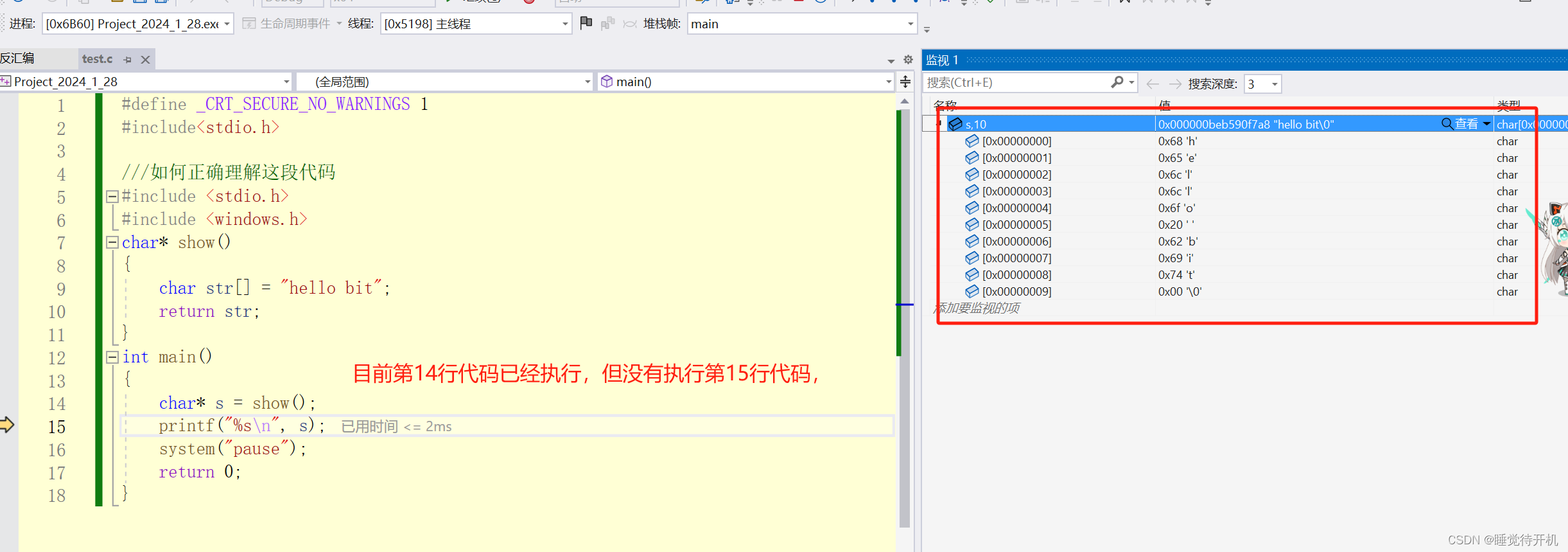
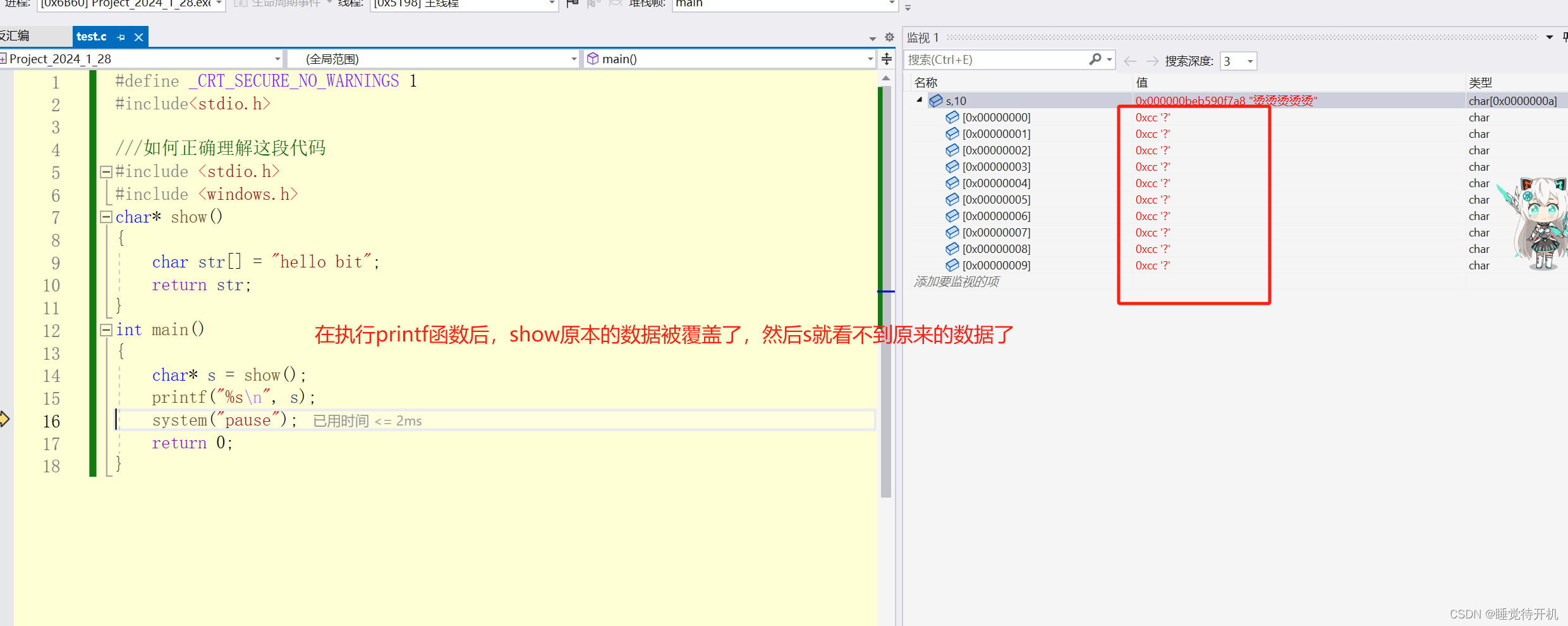
然后最后再说一点,就是函数返回值与函数返回值的接收,是独立的。
完。
相关文章:

【C深度解剖】计算机数据下载和删除原理
简介:本系列博客为C深度解剖系列内容,以某个点为中心进行相关详细拓展 适宜人群:已大体了解C语法同学 作者留言:本博客相关内容如需转载请注明出处,本人学疏才浅,难免存在些许错误,望留言指正 作…...

ASTORS国土安全奖:ManageEngine AD360荣获银奖
美国安全今日(AST)的年度“ASTORS”国土安全奖计划是一个备受瞩目的活动,致力于突显国土安全领域的创新与进步。这一奖项旨在表彰在保护国家免受安全威胁方面做出卓越贡献的个人和组织。该计划汇聚了执法、公共安全和行业领袖,不仅…...

clang--cpplint--gitlint
clang_format clang_format是什么 代码格式化工具 clang_format 官网和官网教程 中文教程 下载 sudo apt install clang sudo apt install clang-format#查看下载是否成功 clang --version 代码的构建到提交的过程: cmake .. make make test make clang_f…...

Web开发8:前后端分离开发
在现代的 Web 开发中,前后端分离开发已经成为了一种常见的架构模式。它的优势在于前端和后端可以独立开发,互不干扰,同时也提供了更好的可扩展性和灵活性。本篇博客将介绍前后端分离开发的概念、优势以及如何实现。 什么是前后端分离开发&am…...
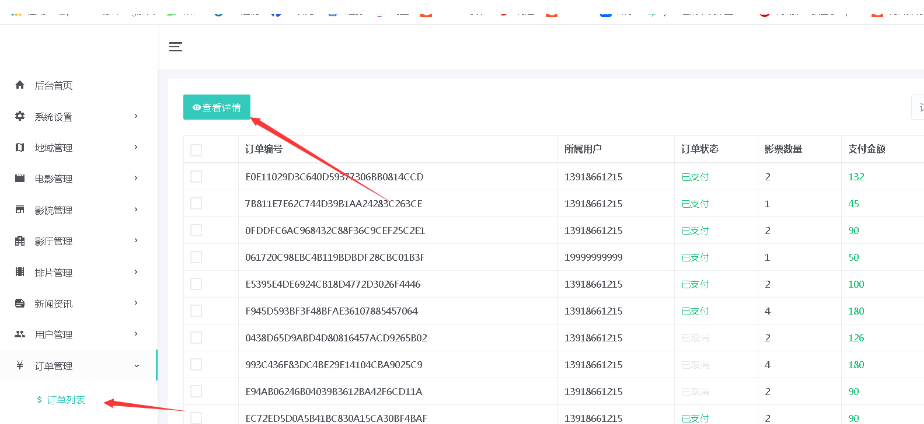
基于 java+springboot+mybatis电影售票网站管理系统前台+后台设计和实现
基于 javaspringbootmybatis电影售票网站管理系统前台后台设计和实现 🍅 作者主页 央顺技术团队 🍅 欢迎点赞 👍 收藏 ⭐留言 📝 🍅 文末获取源码联系方式 📝 🍅 查看下方微信号获取联系方式 承…...
】错误:*.onchip_flash_0:UFM 扇区不支持“隐藏”模式。请更新访问模式设置)
【INTEL(ALTERA)】错误:*.onchip_flash_0:UFM 扇区不支持“隐藏”模式。请更新访问模式设置
说明 由于英特尔 Quartus Prime Standard Edition 软件版本 22.1 存在一个问题,当您针对 10 FPGA Compact 变体英特尔 MAX在片上闪存英特尔 FPGA IP中选择单压缩映像配置模式时,可能会出现以下错误消息。 错误:*.onchip_flash_0:…...

备战蓝桥杯---数据结构与STL应用(基础3)
今天我们主要介绍的是pair,string,set,map pair:我们可以把它当作一个结构体: void solve(){pair<int int> a;//创建amake_pair(1,2);//添加元素cout<<a.first<<endl<<a.second<<endl;}//输出 当然,它也可以嵌套&#…...

「优选算法刷题」:只出现一次的数字Ⅲ
一、题目 给你一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。 你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。 示例 1: …...
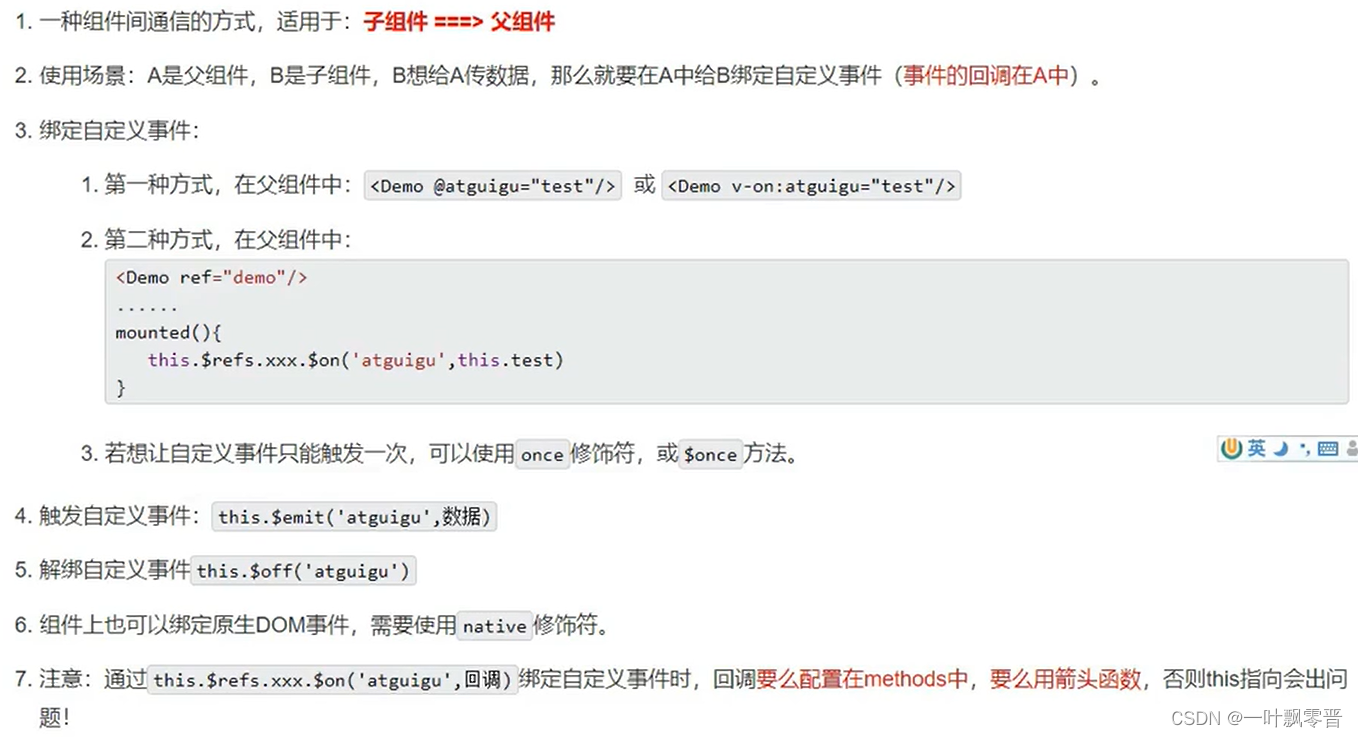
Vue-43、Vue中组件自定义事件
1、给学生绑定atguigu事件 2、在组件内触发事件 第二种写法 传多个参数。 解绑 解绑一个事件 解绑多个自定义事件 this.$off([xxx1,xxx2]);解绑所有事件 this.$off();总结...

GitHub 开启 2FA 双重身份验证的方法
为什么要开启 2FA 自2023年3月13日起,我们登录 GitHub 都会看到一个要求 Enable 2FA 的重要提示,具体如下: GitHub users are now required to enable two-factor authentication as an additional security measure. Your activity on GitHub includes you in this requi…...
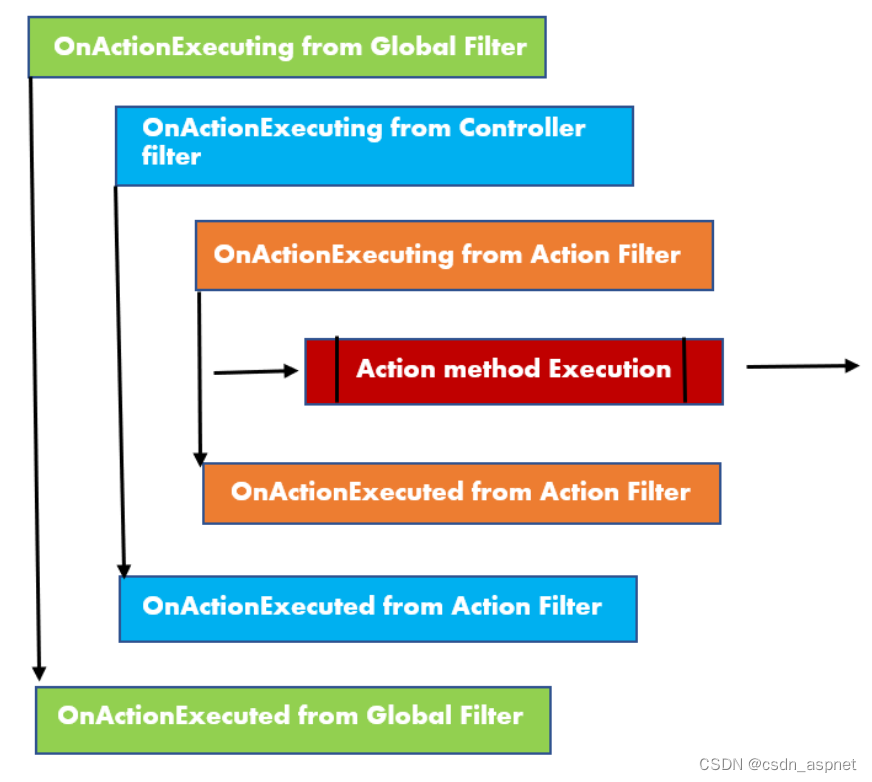
ASP.NET Core 过滤器 使用依赖项注入
过滤器是 ASP.NET Core 中的特殊组件,允许我们在请求管道的特定阶段控制请求的执行。这些过滤器在中间件执行后以及 MVC 中间件匹配路由并调用特定操作时发挥作用。 简而言之,过滤器提供了一种在操作级别自定义应用程序行为的方法。它们就像检查点&#…...

2024年的网创之路应该这样走才对
2024年的网创之路应该这样走才对 大家都知道这两年经济环境不好,钱不好挣,对于普通人,只有一条出路,就是学某项技能,然后死磕,不能提升某项技能的项目,打死也不做,因为多数项目都是…...

ssh异常报错:Did not receive identification string from
一、问题描述 某次外出在异地工作场所xshell炼乳远程服务器时,报错:Connection closed by foreign host. D,服务器查看secure日志或sshd服务状态会显示:id not receive identification string from client_ip; 二、分析处理 1&a…...
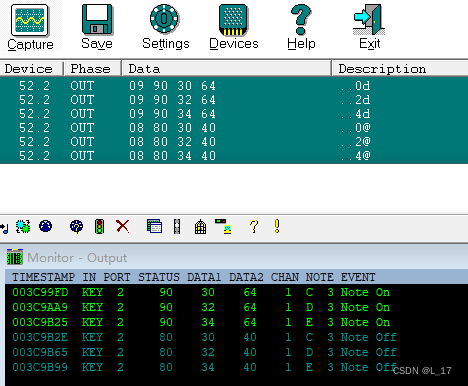
MIDI码深度解析
MIDI 协议即数字音乐接口(Musical Instrument Digital Interface),是电子乐器、合成器等演奏设备之间的一种即时通信协议,用于硬件之间的实时演奏数据传递。如果理解还不够深刻,官方如下解释: 常用midi硬件…...
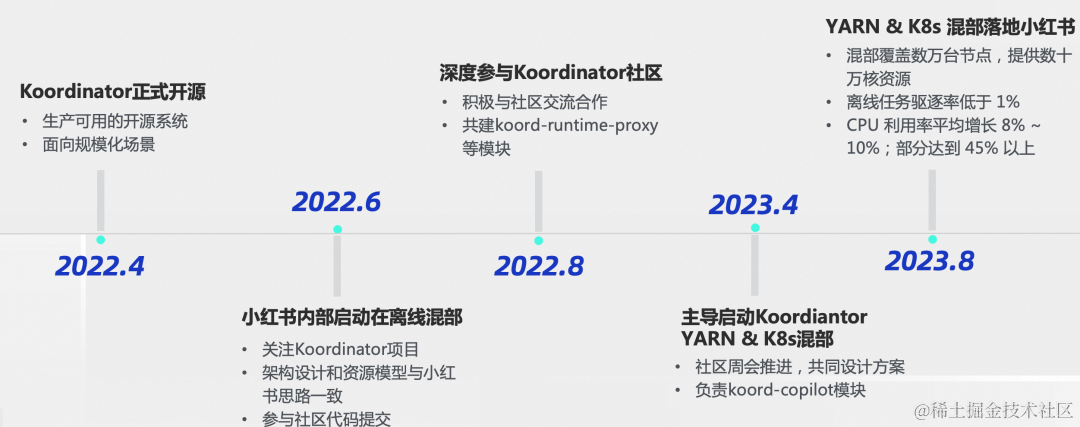
小红书如何做混部?
作者:宋泽辉(小红书)、张佐玮(阿里云) 编者按: Koordinator 是一个开源项目,是基于阿里巴巴内部多年容器调度、混部实践经验孵化诞生,是行业首个生产可用、面向大规模场景的开源混…...
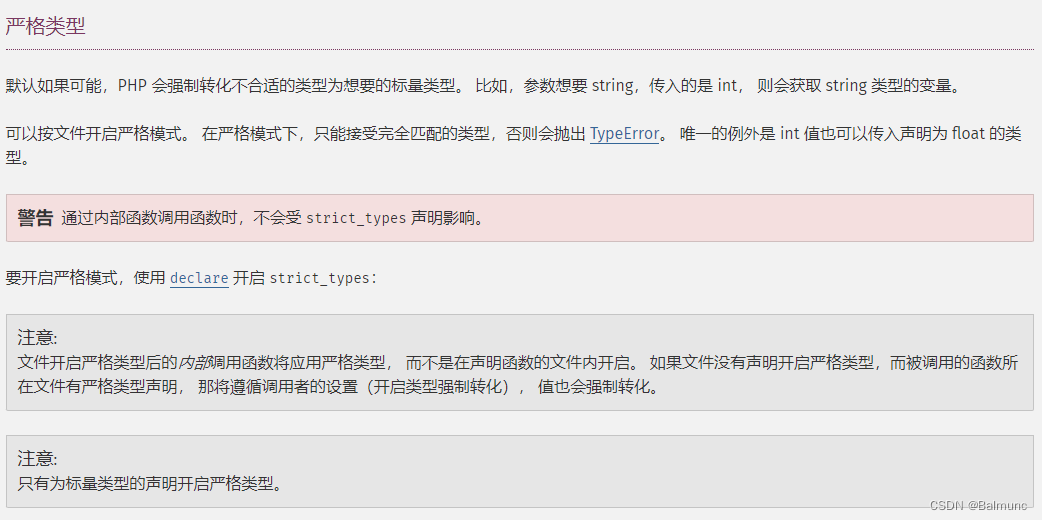
[PHP]严格类型
PHP: 类型声明 - Manual...

作为程序员,你必须学会Maven
资源领取在末尾. Maven 是一款旨在简化 Java 开发流程的管理工具,它的主要功能包括: 1. 项目管理:Maven 提供了一种项目对象模型(Project Object Model, POM),用于管理项目的构建、报告和文档。它允许开发者通过少量代码…...
数据访问宏)
UDF学习(三)数据访问宏
数据访问宏一 网格节点相关宏** NODE_X (v) 节点v的x方向的坐标 (Node *v) NODE_Y (v) 节点v的y方向的坐标 (Node *v) NODE_Z (v) 节点v的z方向的坐标 (Node *v) F_NODE (f,t,n) 获取节点 (face_t f, Thread *t, int n 节点索引号) F_NNODES(f,t) 获取面上的节点数量 (…...

Web3技术革新:重新定义在线体验
互联网的不断演进塑造了我们的数字生活,而Web3技术的涌现正带来一场前所未有的变革。本文将深入探讨Web3技术的创新,以及它如何重新定义和提升我们的在线体验。 Web3技术的基本概念 Web3是互联网的第三个时代,它将去中心化、区块链、智能合约…...

从前端Vue到后端Spring Boot:接收JSON数据的正确姿势
目录 一、前端Vue发送JSON数据二、后端Spring Boot接收JSON数据三、常见错误和问题四、总结 在现代Web开发中,前后端分离已成为一种趋势,Vue和Spring Boot也成为了其中最流行的前后端框架。在Vue前端向Spring Boot后端发送数据时,常常需要将数…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...
