有关平方或高次方的公式整理一元高次方程的求解
Part.I Introduction
这篇博文记录一下数学中常用的有关平方或高次方的一些公式。
Chap.I 一些结论
下面一部分汇总了一些重要的结论
- 完全平方公式:(a±b)2=a2±2ab+b2(a±b)^2=a^2±2ab+b^2(a±b)2=a2±2ab+b2
- 平方差公式:a2−b2=(a+b)(a−b)a^2-b^2=(a+b)(a-b)a2−b2=(a+b)(a−b)
- 三次方公式:(a±b)3=a3±3a2b+3ab2±b3(a±b)^3=a^3±3a^2b+3ab^2±b^3(a±b)3=a3±3a2b+3ab2±b3
- 三次方和的公式:a3+b3=(a+b)(a2−ab+b2)a^3+b^3=(a+b)(a^2-ab+b^2)a3+b3=(a+b)(a2−ab+b2)
- 三次方差的公式:a3−b3=(a−b)(a2+ab+b2)a^3-b^3=(a-b)(a^2+ab+b^2)a3−b3=(a−b)(a2+ab+b2)
- 三次方和减三数乘积:a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−bc−ac)a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ac)a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−bc−ac)
- 二项式定理:(a+b)n=Cn0an+Cn1a(n−1)b+⋯+Cnka(n−k)bk+⋯+Cnnbn(a+b)^n=C^0_na^n+C^1_na^{(n-1)}b+\cdots+C^k_na^{(n-k)}b^k+\cdots+C^n_nb^n(a+b)n=Cn0an+Cn1a(n−1)b+⋯+Cnka(n−k)bk+⋯+Cnnbn
Part.II 两项的 n 次方
Chap.I 和差的 n 次方(二项式定理)
(a+b)2=a2+ab+ba+b2=a2+2ab+b2(a+b)^2=a^2+ab+ba+b^2=a^2+2ab+b^2(a+b)2=a2+ab+ba+b2=a2+2ab+b2 这种完全平方公式大家应该很熟悉吧。但是想对它进行扩充:nnn 项和的 nnn 次方该怎样表示呢?
下面再看两个不同项的 nnn 次方:(a+b)n(a+b)^n(a+b)n,这个展开项有现成的公式,即二项式定理!
(a+b)n=Cn0an+Cn1a(n−1)b+⋯+Cnka(n−k)bk+⋯+Cnnbn(a+b)^n=C^0_na^n+C^1_na^{(n-1)}b+\cdots+C^k_na^{(n-k)}b^k+\cdots+C^n_nb^n(a+b)n=Cn0an+Cn1a(n−1)b+⋯+Cnka(n−k)bk+⋯+Cnnbn
- 二项式系数:Cnk(k=0,⋯,n)C^k_n\ (k=0,\cdots,n)Cnk (k=0,⋯,n)
- 二项式通式:Cnka(n−k)bkC^k_na^{(n-k)}b^kCnka(n−k)bk 是展开式中的第 k+1k+1k+1 项,其通项公式可记作:Tk+1=Cnka(n−k)bkT_{k+1}=C^k_na^{(n-k)}b^kTk+1=Cnka(n−k)bk
Chap.II n 次方的和差
n次方差之差公式:
an−bn=(a−b)(an−1+an−2b+an−3b3+⋯+abn−2+bn−1)a^n-b^n=(a-b)(a^{n-1}+a^{n-2}b+a^{n-3}b^3+\cdots+ab^{n-2}+b^{n-1})an−bn=(a−b)(an−1+an−2b+an−3b3+⋯+abn−2+bn−1)
n次方之和公式。当n为奇数时,
an+bn=(a+b)(an−1−an−2b+an−3b3+⋯−abn−2+bn−1)a^n+b^n=(a+b)(a^{n-1}-a^{n-2}b+a^{n-3}b^3+\cdots-ab^{n-2}+b^{n-1})an+bn=(a+b)(an−1−an−2b+an−3b3+⋯−abn−2+bn−1)
当 n 为偶数时,没有n次方和公式,实际上,n为偶数时
an−bn=(a+b)(an−1−an−2b+an−3b3+⋯−abn−2+bn−1)a^n-b^n=(a+b)(a^{n-1}-a^{n-2}b+a^{n-3}b^3+\cdots-ab^{n-2}+b^{n-1})an−bn=(a+b)(an−1−an−2b+an−3b3+⋯−abn−2+bn−1)
也就是说,当 n 为偶数时,an−bna^n-b^nan−bn 有两种表达形式;只有当n为奇数时,才有n次方之和公式。
Part.III n 个不同项的平方
考虑 nnn 个不同项的平方:(a+b+c+⋯)2=?(a+b+c+\cdots)^2=?(a+b+c+⋯)2=?
这里先不关心展开后每一项的具体内容是什么,首先关心可以展开成多少项,比如 (a+b)2(a+b)^2(a+b)2 在展开后,不整理的话有 444 项,整理之后有 333 项。为什么区分整理前后呢?因为在某些运算规则下,乘法是不具有交换律的,比如矩阵的乘法。下面列一个表格。
| 不同项数目 | 展开整理前 | 展开整理后 |
|---|---|---|
| 2 | 4 | 3 |
| 3 | 9 | 6 |
| 4 | 16 | 10 |
| 5 | 25 | 15 |
| … | ||
| nnn | n2n^2n2 | Cn2+nC^2_n+nCn2+n |
Part.IV 一元高次方程的求解
Chap.I 一次和二次
一元一次方程(又叫一元线性方程)
a1x+x0=0(a1≠0)a_1x+x_0=0\ (a_1\neq 0)a1x+x0=0 (a1=0) 解为 x=−a0/a1x=-a_0/a_1x=−a0/a1
一元二次方程
ax2+bx+c=0(a≠0)ax^2+bx+c=0 (a\neq 0)ax2+bx+c=0(a=0) 其解为 x=−b±b2−4ac2ax=\frac{-b±\sqrt{b^2-4ac}}{2a}x=2a−b±b2−4ac
判别式:Δ=b2−4ac\Delta=b^2-4acΔ=b2−4ac
- Δ>0\Delta>0Δ>0:方程有两个不等的实根
- Δ=0\Delta=0Δ=0:方程有两个相等的实根
- Δ<0\Delta<0Δ<0:方程有两个不等的虚根
韦达定理:设 x1,x2x_1,x_2x1,x2 是方程的两个根
- x1+x2=−bax_1+x_2=-\frac{b}{a}x1+x2=−ab
- x1⋅x2=cax_1\cdot x_2=\frac{c}{a}x1⋅x2=ac
Chap.II 一元三次方程
ax3+bx2+cx+d=0(a≠0)ax^3+bx^2+cx+d=0 (a\neq 0)ax3+bx2+cx+d=0(a=0)
其常用解法是意大利学者卡尔丹于1545年发表的卡尔丹公式法。
特殊形式的求根公式 x3+px2+q=0x^3+px^2+q=0x3+px2+q=0

一般形式的求根公式 卡尔丹法


ps:来源于百度百科,具体推导以后再说。
Chap.III 一元四次方程
ax4+bx3+cx2+dx+e=0(a≠0)ax^4+bx^3+cx^2+dx+e=0 (a\neq 0)ax4+bx3+cx2+dx+e=0(a=0)
一元四次方程的求根公式由意大利数学家费拉里首次提出证明。一元三次方程是在进行了巧妙的换元之后,把问题归结成了一元二次方程从而得解的。于是,如果能够巧妙地把一元四次方程转化为一元三次方程或一元二次方程,就可以利用已知的公式求解了。
ps:公式比较冗长,具体可看百度百科。
相关文章:

有关平方或高次方的公式整理一元高次方程的求解
Part.I Introduction 这篇博文记录一下数学中常用的有关平方或高次方的一些公式。 Chap.I 一些结论 下面一部分汇总了一些重要的结论 完全平方公式:(ab)2a22abb2(ab)^2a^22abb^2(ab)2a22abb2平方差公式:a2−b2(ab)(a−b)a^2-b^2(ab)(a-b)a2−b2(ab)(…...

Java笔记3
ArrayListArrayList<String> list new Arraylist<>();<>是泛型表示存放的数据类型,注意不能是基本数据类型;增删改查增:add 返回值为true删:remove 1.直接删元素2.根据索引删元素改:set(…...

Leetcode.2202 K 次操作后最大化顶端元素
题目链接 Leetcode.2202 K 次操作后最大化顶端元素 Rating : 1717 题目描述 给你一个下标从 0开始的整数数组 nums,它表示一个 栈 ,其中 nums[0]是栈顶的元素。 每一次操作中,你可以执行以下操作 之一 : 如果栈非空…...

JAVA知识点全面总结3:String类的学习
三.String类学习 1.String,StringBuffer,StringBuilder的区别? 2.字符串拼接用加号的原理 ? 3.字符串常量池如何理解? 4.String的intern方法理解? 5.String的equals方法和compareTo方法的使用…...
Eureka注册中心和Nacos注册中心详解以及Nacos与Eureka有什么区别?
目录:前言Eureka注册中心Nacos注册中心Nacos与Eureka有什么区别?前言提供接口给其它微服务调用的微服务叫做服务提供者,而调用其它微服务提供的接口的微服务则是服务消费者。如果服务A调用了服务B,而服务B又调用了服务C࿰…...

Web3D发展趋势以及Web3D应用场景
1,Web3D发展趋势随着互联网的快速发展,Web3D技术也日渐成熟,未来发展趋势也值得关注。以下是Web3D未来发展趋势的七个方面:可视化和可交互性的增强:Web3D可以为三维数据提供可视化和可交互性的增强,将极大地…...

2023-3-4 刷题情况
按位与为零的三元组 题目描述 给你一个整数数组 nums ,返回其中 按位与三元组 的数目。 按位与三元组 是由下标 (i, j, k) 组成的三元组,并满足下述全部条件: 0 < i < nums.length 0 < j < nums.length 0 < k < nums.l…...
前端面试总结
1.引言 最近参加了大量的招聘会,投递了大量的简历,整整体会了从“随便找个厂上一下”——“还是的找个大厂”——“没人要”——“急了急了,海投一波”——“工资有点尬”——“海投中…”。简单说一下自己的一些感受吧,现在的前端属实有点尴…...
: Spatial clustering)
Geospatial Data Science (6): Spatial clustering
Geospatial Data Science (6): Spatial clustering 1.Clustering, spatial clustering, and geodemographics 本节涉及空间观测的统计聚类。许多问题和主题都是复杂的现象,涉及多个维度,难以归纳为一个单一的变量。在统计学术语中,我们把这一类问题称为多变量,而不是在…...

蚁群算法优化问题
%%%%%%%%%%%%蚁群算法解决 TSP 问题%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%% clear all; %清除所有变量 close all; %清图 clc; %清屏 m 50; %蚂蚁个数 Alpha 1; %信息素重要程度参数 Beta 5; %启发式因子重要程度参数 Rho 0.1; %信息素蒸发系数 G 20…...

为啥一个 main 方法就能启动项目
在 Spring Boot 出现之前,我们要运行一个 Java Web 应用,首先需要有一个 Web 容器(例如 Tomcat 或 Jetty),然后将我们的 Web 应用打包后放到容器的相应目录下,最后再启动容器。 在 IDE 中也需要对 Web 容器…...

洛谷:P1554 梦中的统计 JAVA
思路:定义一个长度为10的数组,数组下标代表数组元素的数字,比如arr[0]代表数字0.用一个for循环,对每个数先取余再取整,知道取整得到的数为0,说明该数字已经被拆解完了。今天又学了一个输入,原来…...
C++初学笔记整理
目录 1. C关键字 2. 命名空间 1)命名空间的引入和概述 2)命名空间的定义 3)std与命名空间的使用 4).相关特性 3. C输入&输出 4. 缺省参数 1 )缺省参数概念 2)使用及分类 a.全缺省 b.部分缺省 5. 函数…...

记录--在Vue3这样子写页面更快更高效
这里给大家分享我在网上总结出来的一些知识,希望对大家有所帮助 前言 在开发管理后台过程中,一定会遇到不少了增删改查页面,而这些页面的逻辑大多都是相同的,如获取列表数据,分页,筛选功能这些基本功能。而…...
】测验和作业题部分答案汇总(面向对象篇))
【程序设计与算法(三)】测验和作业题部分答案汇总(面向对象篇)
题目来源:程序设计与算法(三)测验和作业题汇总 文章目录001:简单的swap002:难一点的swap003:好怪异的返回值004:神秘的数组初始化005:编程填空:学生信息处理程序006:奇怪的类复制007:返回什么才好呢008:超简单的复数类009:哪来的输…...
LeetCode 349. 两个数组的交集和 692. 前K个高频单词
两个数组的交集 难度 简单 题目链接 这道题的难度不大,我们可以把数组里的数据存到set里面。这样就完成了排序和去重,然后我们再把一个set里面的数据和另外一个set数据进行比较。如果相同就插入到数组里。 代码如下: 但是这个算法的时间复…...
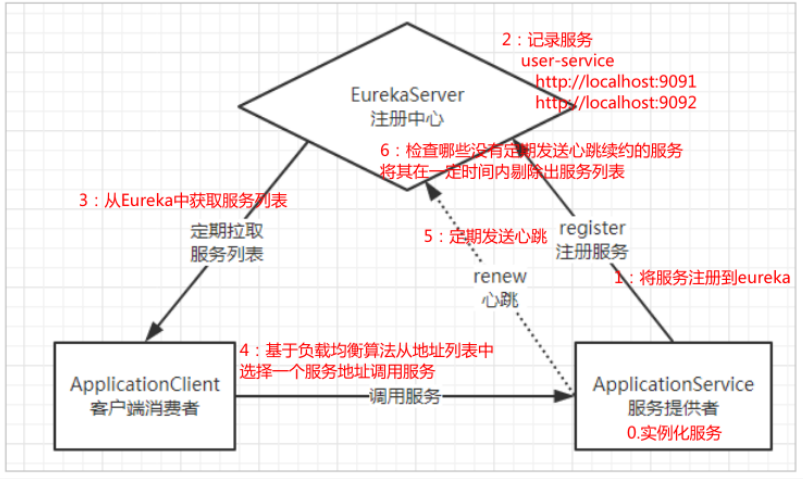
SpringCloud的五大组件功能
SpringCloud的五大组件 EurekaRibbonHystrixZuulConfig 一、Eureka 作用是实现服务治理,即服务注册与发现。 Eureka服务器相当于一个中介,负责管理、记录服务提供者的信息。服务调用者不需要自己寻找服务 ,而是把需求告诉Eureka &#x…...

剑指 Offer II 016. 不含重复字符的最长子字符串
题目链接 剑指 Offer II 016. 不含重复字符的最长子字符串 mid 题目描述 给定一个字符串 s,请你找出其中不含有重复字符的 最长连续子字符串 的长度。 示例 1: 输入: s “abcabcbb” 输出: 3 解释: 因为无重复字符的最长子字符串是 “abc”,所以其长度…...
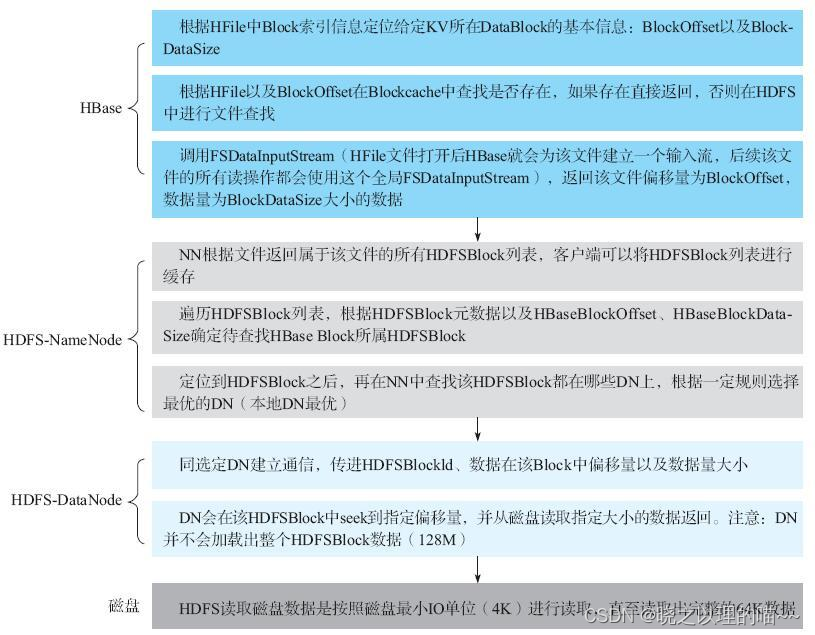
HBase读取流程详解
读流程从头到尾可以分为如下4个步骤:Client-Server读取交互逻辑,Server端Scan框架体系,过滤淘汰不符合查询条件的HFile,从HFile中读取待查找Key。其中Client-Server交互逻辑主要介绍HBase客户端在整个scan请求的过程中是如何与服务…...

Redis学习(一):NoSQL概述
为什么要使用Nosql 现在是大数据时代,过大的数据一般的数据库无法进行分析处理了。 单机MySQL的年代 90年代,一个基本的网站访问量一般不会太大,单个数据库完全足够! 那个时候,更多的去使用静态网站,服务器…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
