【leetcode题解C++】257.二叉树的所有路径 and 404.左叶子之和 and 112.路径总和
257. 二叉树的所有路径
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1:

输入:root = [1,2,3,null,5] 输出:["1->2->5","1->3"]
示例 2:
输入:root = [1] 输出:["1"]
思路:递归,结束条件是一个结点没有左孩子和右孩子。题目提示中写到至少会有一个根节点,那么不用判断树空的情况。
代码实现:
class Solution {void generate(TreeNode *node, string path, vector<string> &result) {path += to_string(node->val);if(node->left && !node->left->left && !node->left->right) {result.push_back(path);return;}if(node->left) generate(node->left, path + "->", result);if(node->right) generate(node->right, path + "->", result);} vector<string> binaryTreePaths(TreeNode* root) {string path = "";vector<string> result;//if(!root) return result;generate(root, path, result);return result;}
};404. 左叶子之和
给定二叉树的根节点 root ,返回所有左叶子之和。
示例 1:

输入: root = [3,9,20,null,null,15,7] 输出: 24 解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
示例 2:
输入: root = [1] 输出: 0
思路:递归,迭代都可以。迭代的话,前中后续都可行,下面的代码是后序遍历,注意判断左叶子结点即可。递归的判定条件也是相同的。
代码实现1:迭代
class Solution {
public:int sumOfLeftLeaves(TreeNode* root) {stack<TreeNode *> stk;if(!root) return 0;stk.push(root);int ret = 0;TreeNode *node;while(!stk.empty()) {node = stk.top();stk.pop();if(node->left && !node->left->left && !node->left->right) ret += node->left->val;if(node->left) stk.push(node->left);if(node->right) stk.push(node->right);}return ret;}
};代码实现2:递归
class Solution {
public:int sumOfLeftLeaves(TreeNode* root) {if(!root) return 0;int leftValue = 0;if(root->left && !root->left->left && !root->left->right) {leftValue = root->left->val;}return leftValue + sumOfLeftLeaves(root->left) + sumOfLeftLeaves(root->right);}
};
112. 路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
示例 1:

输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22 输出:true 解释:等于目标和的根节点到叶节点路径如上图所示。
示例 2:
输入:root = [1,2,3], targetSum = 5 输出:false 解释:树中存在两条根节点到叶子节点的路径: (1 --> 2): 和为 3 (1 --> 3): 和为 4 不存在 sum = 5 的根节点到叶子节点的路径。
示例 3:
输入:root = [], targetSum = 0 输出:false 解释:由于树是空的,所以不存在根节点到叶子节点的路径。
思路:递归+回溯,当得到的结果不满足时,需要往回退一步,寻找新的可能满足需求的路径。
代码实现:
class Solution {
public:bool calculate(TreeNode *node, int count) {if(!node->left && !node->right && count == 0) return true;if(!node->left && !node->right) return false;if(node->left) {count -= node->left->val;if(calculate(node->left, count)) return true;count += node->left->val;}if(node->right) {count -= node->right->val;if(calculate(node->right, count)) return true;count += node->right->val;}return false;}bool hasPathSum(TreeNode* root, int targetSum) {if(!root) return false;return calculate(root, targetSum - root->val);}
};相关文章:

【leetcode题解C++】257.二叉树的所有路径 and 404.左叶子之和 and 112.路径总和
257. 二叉树的所有路径 给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。 叶子节点 是指没有子节点的节点。 示例 1: 输入:root [1,2,3,null,5] 输出:["1->2->5",&…...
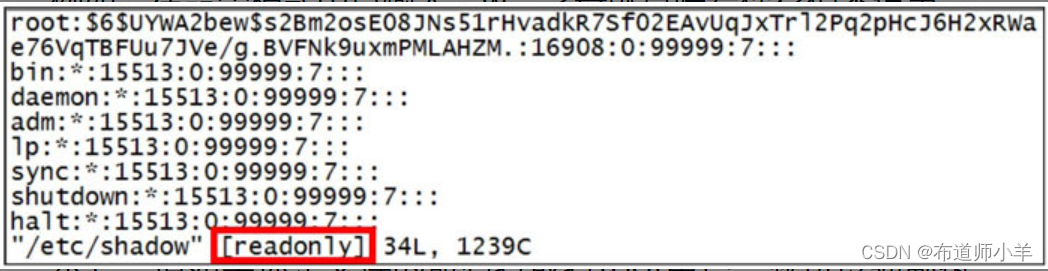
Linux——文本编辑器Vim
Linux中的所有内容以文件形式管理,在命令行下更改文件内容,常常会用到文本编辑器。我们首选的文本编辑器是Vim,它是一个基于文本界面的编辑工具,使用简单且功能强大,更重要的是,Vim是所有Linux发行版本的默…...
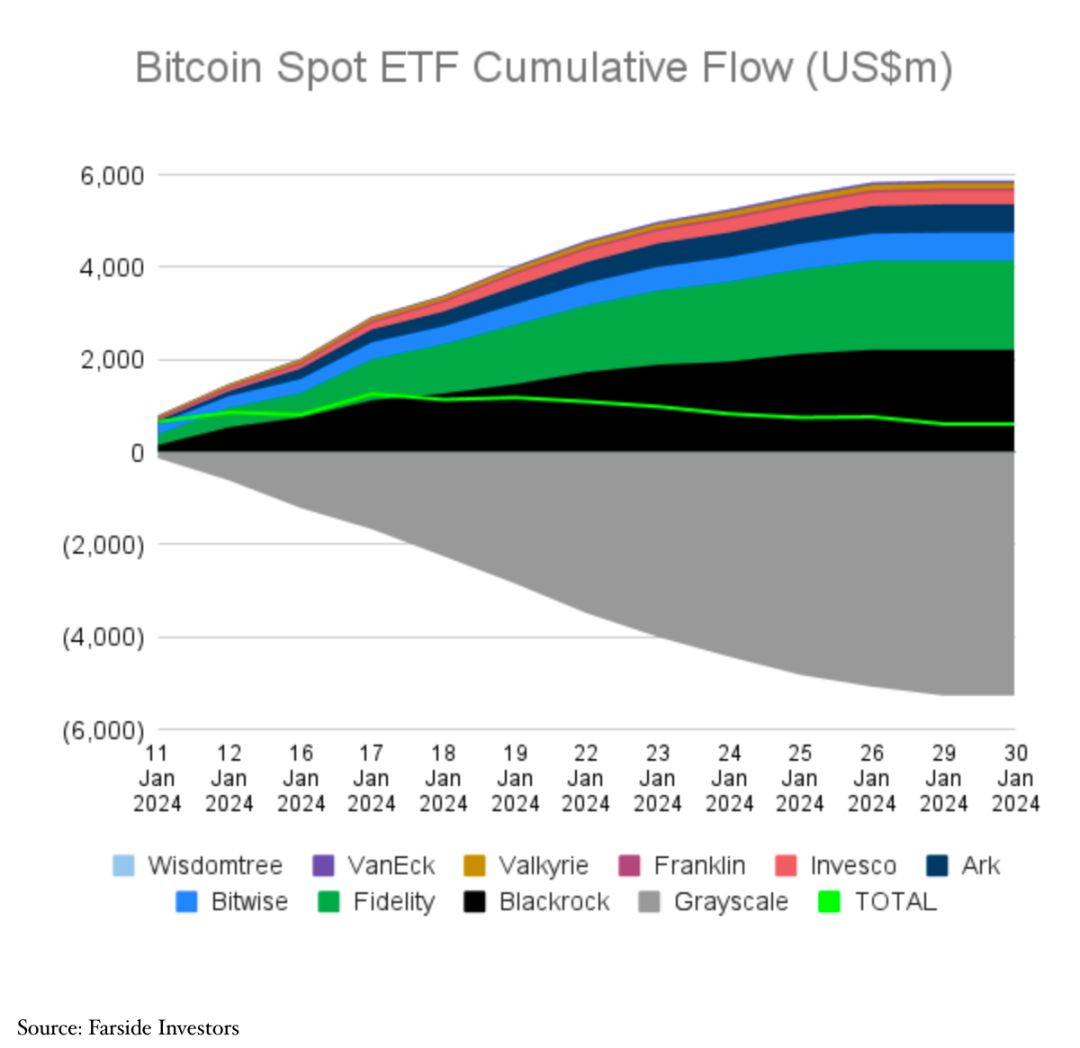
以“美”为鉴,探寻香港比特币现货ETF的未来发展
出品|欧科云链研究院 作者|Hedy Bi 根据The Block于1月29日的报道,嘉实国际成为了首家向香港证监会提交比特币现货ETF申请的机构。早在去年12月22日,香港证监会发布了《有关证监会认可基金投资虚拟资产的通函》,明确…...
)
Unity项目打包的方法(之一)
在 Unity 中,将项目打包成 .unitypackage 文件和直接压缩 Assets、Packages 和 ProjectSettings 目录有几个关键区别,主要体现在打包方式、使用目的和包含的内容上。 打包成 UnityPackage .unitypackage 是 Unity 的一种打包格式,它允许你将项…...

如何安装MySQL
如何安装MySQL 前提条件下载MySQL在 Windows 上安装 MySQL验证 MySQL 安装 MySQL是当今工业界广泛使用的最流行的关系数据库管理软件之一。它通过各种存储引擎提供多用户访问支持。它得到了甲骨文公司的支持。在本节中,我们将学习如何为初学者下载和安装 MySQL。 前…...

如何编写.gitignore文件
文章目录 前端架构师教你如何编写.gitignore文件.gitignore文件简介.gitignore文件的语法规则.gitignore文件的最佳实践常见问题与解决 前端架构师教你如何编写.gitignore文件 .gitignore文件简介 .gitignore文件是Git版本控制系统中一个非常有用的工具。它可以指定一组文件或…...
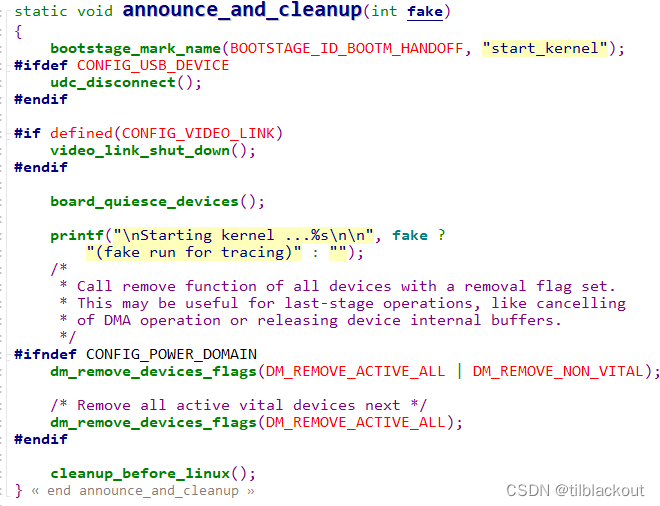
U-Boot学习(7):内核启动之bootz启动zImage源码分析
在上一节中,我们分析了U-BOOT初始化的流程,最后就是进入U-Boot的命令行中执行了,如果用户没有任何操作,则经过固定延时后将执行默认的bootcmd环境变量里的指令,那这里面肯定就是启动内核了。在U-BOOT简介及命令行指令详…...

[GN] DP学习笔记板子
文章目录 Bitset滚动数组多重背包区间DP树形dp状压dp模拟退火 Bitset 使用bitset需要引用<bitset>头文件。 其声明方法为: std::bitset<N>s; (N为s长度)常用函数: b.any() 判断b中是否存在值为1的二进制位 b.none() 判断b中是否不存在值为1的二…...
GLog开源库使用
Glog地址:https://github.com/google/glog 官方文档:http://google-glog.googlecode.com/svn/trunk/doc/glog.html 1.利用CMake进行编译,生成VS解决方案 (1)在glog-master文件夹内新建一个build文件夹,用…...
微信小程序如何实现点击上传图片功能
如下所示,实际需求中常常存在需要点击上传图片的功能,上传前显示边框表面图片显示大小,上传后将图形缩放到边框大小。 实现如下: .wxml <view class="{{img_src==?blank-area:}}" style="width:100%;height:40%;display:flex;align-items: center;jus…...
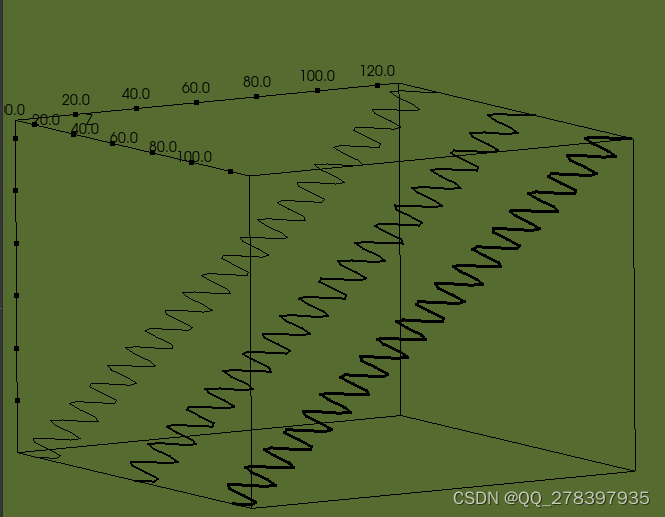
Windows Qt C++ VTK 绘制三维曲线
Qt 自带数据可视化从文档上看,只能实现三维曲面。 QwtPlot3D在Qt6.6.0上没编译通过。 QCustomPlot 只能搞二维。 VTK~搞起。抄官网demo。 后续需求: 1、对数轴 2、Y轴逆序 3、Z轴值给色带,类似等高线图的色带 期待各位大佬多多指导。…...

Android T 远程动画显示流程(更新中)
序 本地动画和远程动画区别是什么? 本地动画:自给自足。对自身SurfaceControl矢量动画进行控制。 远程动画:拿来吧你!一个app A对另一个app B通过binder跨进程通信,控制app B的SurfaceControl矢量动画。 无论是本地动画还是远程…...

【计算机网络】【练习题及解答】【新加坡南洋理工大学】【Computer Control Network】
说明: 仅供学习使用。 一、题目描述 题目共4问,描述网络通信中的 帧传输时延(Frame Delay)、传播时延(Propagation Delay),以及 链接利用率(Link Utilization) 的相关…...

云计算HCIE备考经验分享
大家好,我是来自深圳信息职业技术学院22级鲲鹏3-1班的刘同学,在2023年9月19日成功通过了华为云计算HCIE认证,并且取得了A的成绩。下面把我的考证经验分享给大家。 转专业进鲲鹏班考HCIE 大一上学期的时候,在上Linux课程的时候&…...

Threejs API——`OrbitControls`相机控件
文章目录 API用法API OrbitControls 相机控制用法 导入import {OrbitControls } from three/examples/jsm/controls/OrbitControls.js import {DRACOLoader,AmbientLight,Color,MOUSE,...

远程教育:低代码在教育技术领域的重塑之力
新冠肺炎大流行对世界各地的行业产生了影响,其中一些行业的影响远远超过其他行业。食品、零售、供应链、娱乐和航空业是受影响最大的行业,为确保不间断运营,这引发了一场数字革命。相信,这种数字化的采用将长期保持下去࿰…...

vue 模板语法值class操作
class.html <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>class</title><!-- 确保引入正确的Vue版本库,下面只是示例,需要替换为实际可工作的CDN地址 --><sc…...
MySQL的原生API实现插入数据后在可视化工具上不显示的问题解决
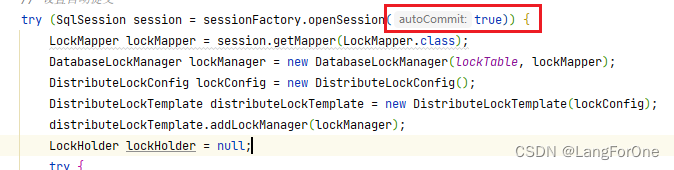
显示表中有两行数据,该表也设置了主键和唯一索引 点进表里看却没有数据 问题原因出现在这里,虽然很多常用的数据库连接池都会开启自动提交,但ibatis的SqlSession使用sessionFactory.openSession()创建时,默认的自动提交是false&am…...
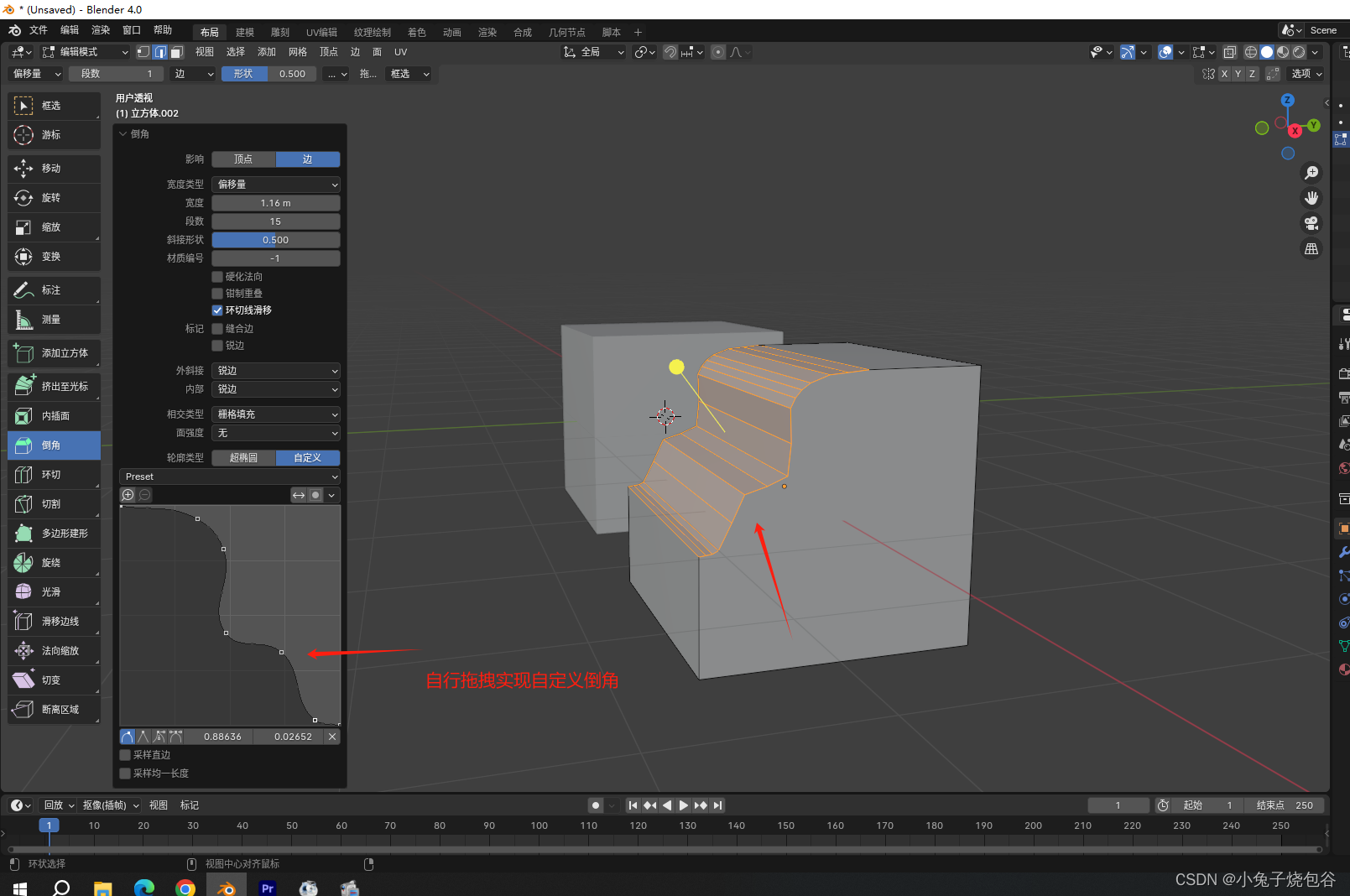
Blender教程(基础)-内插面、分离、环切、倒角-08
一、内插面 菜单位置如下图位置。 单击需要处理的面,出现一个黄色的圈。 1、菜单选中内插 鼠标悬停在黄色圈内单击左键可以来回实现内插,但是发现并不好操作。 2、快捷键内插 在选中需要操作的面之后,鼠标移动到外面,键盘在英…...

Unity 自动轮播、滑动轮播
如图所示,可设置轮播间隔,可左右滑动进行轮播 1.在UGUI创建个Image,添加自动水平组件 2.添加并配置脚本 3.代码如下,都有注释 using UnityEngine; using UnityEngine.UI;public class IndicatorManager : MonoBehaviour {public …...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...
