AtCoder Beginner Contest 338F - Negative Traveling Salesman【floyd+状态压缩dp】
原题链接:https://atcoder.jp/contests/abc338/tasks/abc338_f
Time Limit: 6 sec / Memory Limit: 1024 MB
Score: 500 points、
问题陈述
有一个有N个顶点和M条边的加权简单有向图。顶点的编号为 1 到 N,i/th 边的权重为 Wi,从顶点 Ui 延伸到顶点Vi。权重可以为负,但该图不包含负循环。
确定是否存在至少访问每个顶点一次的行走。如果存在这样的行走,请找出所遍历的边的最小总权重。如果同一条边被多次遍历,则每次遍历都要加上这条边的权重。
这里的 "至少访问每个顶点一次的行走 "是指满足以下两个条件的顶点序列v1,v2,…,vk:
- 对于每个 i 有一条边从顶点 vi 延伸到顶点 vi+1。
- 对于每个 j (1≤j≤N) 都有 i (1≤i≤k) 这样的边 vi=j 。
限制因素
- 2≤N≤20
- 1≤M≤N(N−1)
- 1≤Ui,Vi≤N
- Ui
Vi
- (Ui,Vi)
(Uj,Vj)
- −1e6≤Wi≤1e6
- 给定图形不包含负循环。
- 所有输入值均为整数。
输入输出描述
Sample Input 1Copy
3 4 1 2 5 2 1 -3 2 3 -4 3 1 100
Sample Output 1Copy
-2
按照 2→1→2→3 的顺序跟随顶点,可以访问所有顶点至少一次,所遍历的边的总重量为 (−3)+5+(−4)=−2。这是最小值。
Sample Input 2Copy
3 2 1 2 0 2 1 0
Sample Output 2Copy
No
没有至少访问所有顶点一次的行走。
Sample Input 3Copy
5 9 1 2 -246288 4 5 -222742 3 1 246288 3 4 947824 5 2 -178721 4 3 -947824 5 4 756570 2 5 707902 5 1 36781
Sample Output 3Copy
-449429
解题思路:
首先题目要求我们至少经过每个点一次,也就是说我们只要找到一条路径经过了每个点并且这条路径权值总和最小,也就是说我们并不关心每个点经过了几次,只要经过了就行了,例如如果我们找到了一条权值总和最小并且经过所有点至少一次的路径a->b->c->b->d,我们考虑的路径集合应该是a->b->c->d,,也就是说c->b->d中间的b只是c->d最短路径经过的一个点而已,也就是说我们只需要考虑走过每个点的顺序即可,确定了顺序之后,任意俩个点之间的距离应该使用最短路径,由于不存在负环,任意俩个点之间肯定是存在最短路径的,并且最短路径的长度肯定是确定的,这个题目点的个数最多只有20个,对于考虑哪种走的顺序总路径最短,我们可以考虑状态压缩dp,然后需要提前预处理任意俩个点之间的最短路,可以采用floyd算法才求任意俩点之间的最短路径,预处理之后状态压缩dp处理即可,具体分析见代码处。
状态压缩dp处理过程
状态定义:
定义f[i][j]表示当前走的点的集合为i,并且走过的最后一个点为j的所有方案的最短路径。
初始化:
f[1<<i][i]=0,当前集合只有一个点,就是起点。
状态转移:
当前走过的最后一个点是j,需要考虑倒数第二个点k,用来转移
f[i][j]=min(f[i^(1<<j][k]+d[k][j])
最终答案:
最终走过的点的集合肯定是(1<<n)-1,然后走过的最后一个点可以是任意一个点,所以答案就是min(f[(1<<n)-1][i]) (0<i<n)
时间复杂度:floyd预处理时间复杂度为O(n^3),n=20,这个时间大概是8e3,状态压缩dp处理时间复杂度为O((2^n)*n*n),这个时间大概为4e8,这个时间复杂度很高了,但是这个题目给了6s的时间,所以是可以过的,最终是时间复杂度为O((n^3)+(2^n)*n*n)。
空间复杂度:d数组空间为O(n^2),dp数组f空间为O((2^n)*n),最终空间复杂度为O((n^2)+(2^n)*n),空间大概是(20^2+(2^20)*20),大概是2e7*4/1e6=80M,这个题目给了1024M,空间肯定是足够的。
cpp代码如下:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 25, M = 1 << 20, INF = 0x3f3f3f3f;int n, m;
int d[N][N], f[M][N];void floyd()
{for (int k = 0; k < n; k++)for (int i = 0; i < n; i++)for (int j = 0; j < n; j++){if (d[i][k] == INF || d[k][j] == INF)continue;d[i][j] = min(d[i][j], d[i][k] + d[k][j]);}
}
int main()
{cin >> n >> m;for (int i = 0; i < n; i++)for (int j = 0; j < n; j++)if (i == j)d[i][j] = 0;elsed[i][j] = INF;for (int i = 0; i < m; i++){int u, v, w;scanf("%d%d%d", &u, &v, &w);u--, v--;d[u][v] = w; //题目说了不存在重边。所以这里可以直接赋值,如果存在重边应该取所有重边的最小值}//floyd预处理任意俩个点之间的最短路floyd();memset(f, 0x3f, sizeof f);//初始之起点for (int i = 0; i < n; i++)f[1 << i][i] = 0;//状态压缩dp处理过程for (int i = 0; i < 1 << n; i++) //第一维枚举走过的点的集合for (int j = 0; j < n; j++) //第二维枚举当前走的点的集合中的最后一个点{if (~i >> j & 1) //当前最后一个点是j,那么当前走过的点的集合必须包含j,continue;for (int k = 0; k < n; k++){if (j == k) //不可能自己走到自己continue;if (~i >> k & 1) //前一个点是k,所以当前走过的点的集合i中必须包含kcontinue;if (f[i ^ (1 << j)][k] == INF || d[k][j] == INF) //INF表示某种状态不存在或者俩个点之间不存在边,不能用于转移continue;f[i][j] = min(f[i][j], f[i ^ (1 << j)][k] + d[k][j]);}}int ans = INF;//当前走过的点的集合肯定是(1<<n)-1,最后一个点可以是任意一个点for (int i = 0; i < n; i++)ans = min(ans, f[(1 << n) - 1][i]);if (ans == INF) //不存在走过每个点至少一次的路径,输出Noputs("No");else //存在走过每个点至少一次的路径,输出最短路径的长度cout << ans << endl;return 0;
}相关文章:
AtCoder Beginner Contest 338F - Negative Traveling Salesman【floyd+状态压缩dp】
原题链接:https://atcoder.jp/contests/abc338/tasks/abc338_f Time Limit: 6 sec / Memory Limit: 1024 MB Score: 500 points、 问题陈述 有一个有N个顶点和M条边的加权简单有向图。顶点的编号为 1 到 N,i/th 边的权重为 Wi,从顶点 U…...
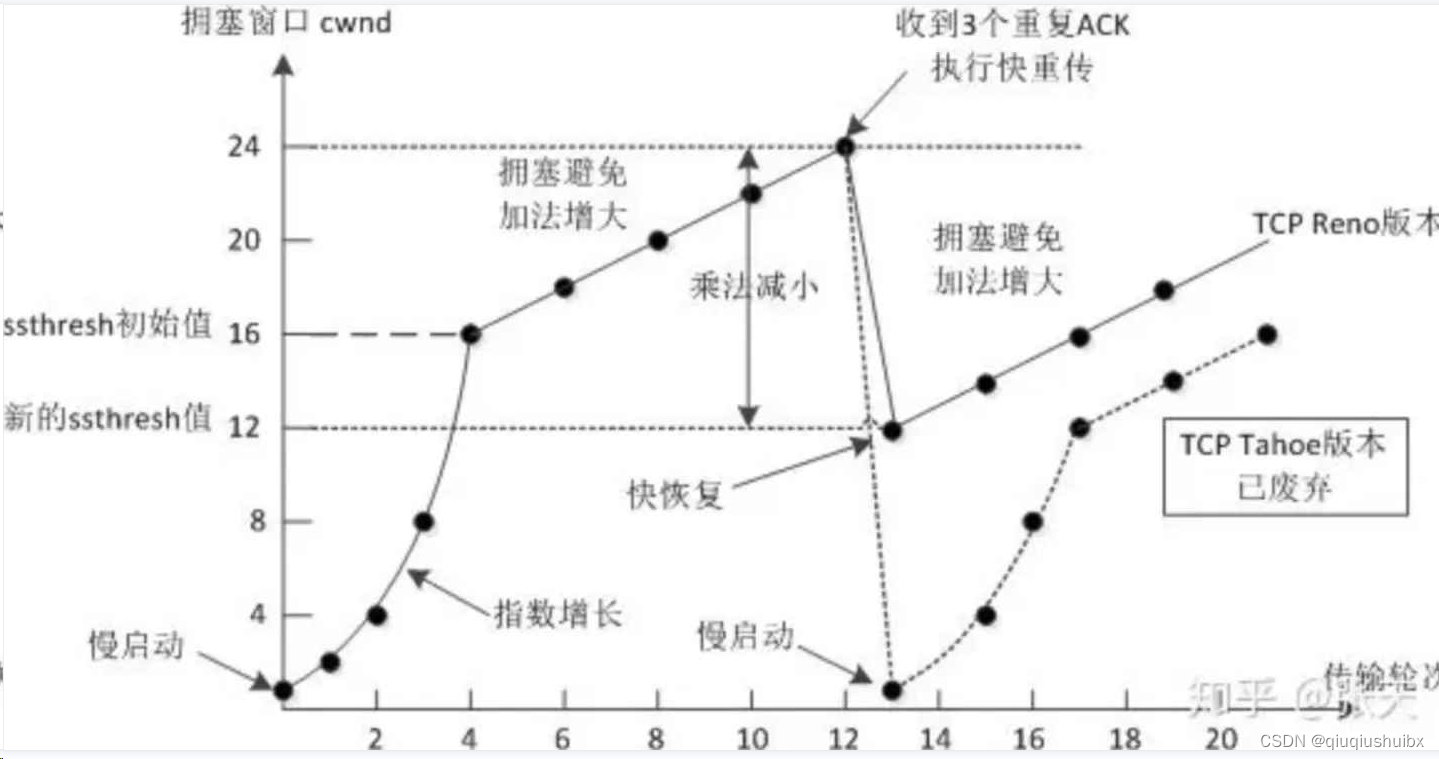
UDP/TCP协议特点
1.前置知识 定义应用层协议 1.确定客户端和服务端要传递哪些信息 2.约定传输格式 网络上传输的一般是二进制数据/字符串 结构化数据转二进制/字符串 称为序列化 反之称之为反序列化 下面就是传输层了 在TCP/IP协议中,我们以 目的端口,目的IP 源端口 源IP 协议号这样一个五…...

编程笔记 html5cssjs 059 css多列
编程笔记 html5&css&js 059 css多列 一、CSS3 多列属性二、实例小结 CSS3 可以将文本内容设计成像报纸一样的多列布局. 一、CSS3 多列属性 下表列出了所有 CSS3 的多列属性: 属性 描述 column-count 指定元素应该被分割的列数。 column-fill 指定如何填充…...

Facebook的元宇宙探索:虚拟社交的新时代
近年来,科技的飞速发展推动着人类社交方式的翻天覆地的改变。在这场数字化革命的浪潮中,社交媒体巨头Facebook正积极探索并引领着一个被誉为“元宇宙”的全新领域,试图为用户打造更为真实、丰富的虚拟社交体验。 元宇宙的崛起 元宇宙这个概念…...

用React给XXL-JOB开发一个新皮肤(四):实现用户管理模块
目录 一. 简述二. 模块规划 2.1. 页面规划2.2. 模型实体定义 三. 模块实现 3.1. 用户分页搜索3.2. Modal 配置3.3. 创建用户表单3.4. 修改用户表单3.5. 删除 四. 结束语 一. 简述 上一篇文章我们实现登录页面和管理页面的 Layout 骨架,并对接登录和登出接口。这篇…...

某赛通电子文档安全管理系统 hiddenWatermark/uploadFile 文件上传漏洞复现
0x01 产品简介 某赛通电子文档安全管理系统(简称:CDG)是一款电子文档安全加密软件,该系统利用驱动层透明加密技术,通过对电子文档的加密保护,防止内部员工泄密和外部人员非法窃取企业核心重要数据资产,对电子文档进行全生命周期防护,系统具有透明加密、主动加密、智能…...

Redis五种数据类型及应用场景
1、数据类型 String(字符串,整数,浮点数):做简单的键值对缓存 List(列表):储存一些列表类型的数据结构 Hash(哈希):包含键值对的无序散列表,结构化的数据 Set(无序集合):交集,并集…...
测试环境搭建整套大数据系统(一:基础配置,修改hostname,hosts,免密)
一:使用服务器配置。 二:修改服务器名称hostname,hosts。 在 Linux 系统中,hostname 和 /etc/hosts 文件分别用于管理主机名和主机名解析。 在三台服务器上,分别执行以下命令。 vim /etc/hostnamexdso-hadoop-test-0…...
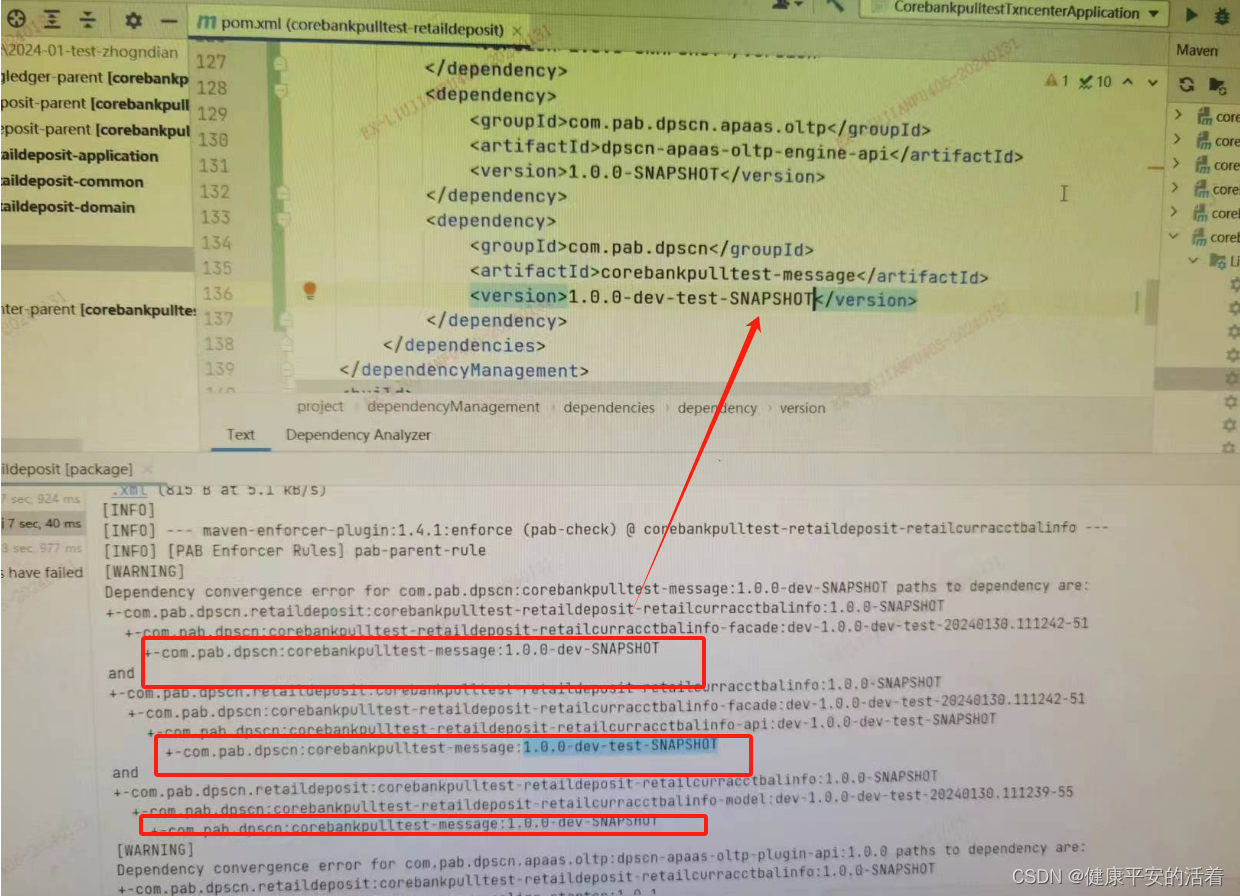
maven helper 解决jar包冲突方法
一 概要说明 1.1 说明 首先,解决idea中jar包冲突,使用maven的插件:maven helper插件,它能够给我们罗列出来同一个jar包的不同版本,以及他们的来源,但是对不同jar包中同名的类没有办法。 1.2 依赖顺序 …...
)
AppSrv-文件共享(23国赛真题)
2023全国职业院校技能大赛网络系统管理赛项–模块B:服务部署(WindowServer2022) 文章目录 AppSrv-文件共享题目配置步骤创建用户主目录共享文件夹:本地目录为d:\share\users\,允许所有域用户可读可写。在本目录下为所有用户添加一个以名称命名的文件夹,该文件夹将设置为所…...

AsyncLocal是如何实现在Thread直接传值的?
一:背景 1. 讲故事 这个问题的由来是在.NET高级调试训练营第十期分享ThreadStatic底层玩法的时候,有朋友提出了AsyncLocal是如何实现的,虽然做了口头上的表述,但总还是会不具体,所以觉得有必要用文字图表的方式来系统…...
Flask 入门1:一个简单的 Web 程序
1. 关于 Flask Flask诞生于2010年, Armin Ronacher的一个愚人节玩笑。不过现在已经是一个用python语言基于Werkzeug工具箱编写的轻量级web开发框架,它主要面向需求简单,项目周期短的小应用。 Flask本身相当于一个内核,其他几乎所…...
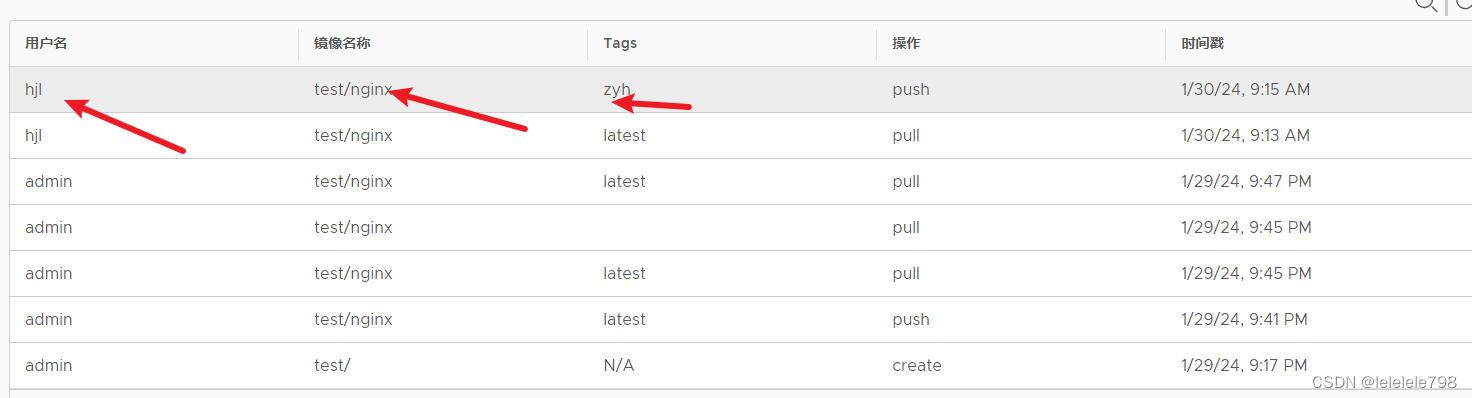
维护管理Harbor,docker容器的重启策略
维护管理Harbor 通过HarborWeb创建项目 在 Harbor 仓库中,任何镜像在被 push 到 regsitry 之前都必须有一个自己所属的项目。 单击“项目”,填写项目名称,项目级别若设置为"私有",则不勾选。如果设置为公共仓库&#…...
Qt6入门教程 14:QToolButton
目录 一.简介 二.常用接口 1.void setMenu(QMenu * menu) 2.void setPopupMode(ToolButtonPopupMode mode) 3.void setToolButtonStyle(Qt::ToolButtonStyle style) 4.void setArrowType(Qt::ArrowType type) 5.void setDefaultAction(QAction * action) 三.实战演练 1…...
3D数据转换器HOOPS Exchange如何获取模型的几何数据? 干货预警!
一、概述 前面讲解过模型在内存中的结构,现在回顾一下,当模型导入成功后,整个模型数据会以原生结构的 PRC 组装树形式存放到内存中。(申请 HOOPS Exchange 试用) PRC结构的主要类型包含四种,分别是…...

Coremail启动鸿蒙原生应用开发,打造全场景邮件办公新体验
1月18日,华为在深圳举行鸿蒙生态千帆启航仪式,Coremail出席仪式并与华为签署鸿蒙合作协议,宣布正式启动鸿蒙原生应用开发。作为首批拥抱鸿蒙的邮件领域伙伴,Coremail的加入标志着鸿蒙生态版图进一步完善。 Coremail是国内自建邮件…...

基于CVITEK_CV1821+SOI_Q03P的IPC方案
方案概述: 该方案基于主控平台CVITEK_CV1821和sensor SOI_Q03P,运用于智能监控IP摄像头,可用于户外或室内。采用了2304x1296的分辨率,30的帧率,支持HDR。作为3M的监控摄像头,通过ISP图像调校技术ÿ…...

chromedriver安装和环境变量配置
chromedriver 1、安装2、【重点】环境变量配置(1)包的复制:(2)系统环境变量配置 3、验证 1、安装 网上随便搜一篇chromedriver的安装文档即可。这里是一个快速链接 特别提醒:截止2024.1.30,chr…...

Linux浅学笔记03
目录 有关root的命令 用户和用户组 用户组管理:(以下需要root用户执行) 创建用户组: 删除用户组: 用户管理:(以下需要root用户执行) 创建用户: 删除用户: 查看用…...
【vue】图片加载骨架
一、前言 在网速较低或者网站的服务器宽带只有几MB的情况下,网页中的图片加载时,要么空白,要么像打印机一样一行一行地“扫描”出来,为了提升用户体验,可以给图片标签外加一层骨架。 无骨架 有骨架 二、详细设计 每张…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
