编曲学习:和声音程 调式体系 唱名法 调式调性
34届和声音程 调式体系 唱名法 调式调性![]() https://app8epdhy0u9502.pc.xiaoe-tech.com/live_pc/l_65af994be4b064a8cb1c3a5f?course_id=course_2XLKtQnQx9GrQHac7OPmHD9tqbv
https://app8epdhy0u9502.pc.xiaoe-tech.com/live_pc/l_65af994be4b064a8cb1c3a5f?course_id=course_2XLKtQnQx9GrQHac7OPmHD9tqbv
34届独立音乐人编曲训练营![]() https://app8epdhy0u9502.pc.xiaoe-tech.com/p/t_pc/course_pc_detail/camp_pro/course_2XLKtQnQx9GrQHac7OPmHD9tqbv
https://app8epdhy0u9502.pc.xiaoe-tech.com/p/t_pc/course_pc_detail/camp_pro/course_2XLKtQnQx9GrQHac7OPmHD9tqbv
音级、音程、度数
基本音级
1234567

音程
两个音在音高上的关系、距离叫做音程,单位为度
比如C3和G3有什么关系?有音程关系!

度数
低音到高音、包含几个音级,就是几度
C3到G3是5度音程,因为有C3,D3,E3,F3,G3这5个音
(含头与含尾,并且不带升降号的音名),可以看最左边钢琴的白键!
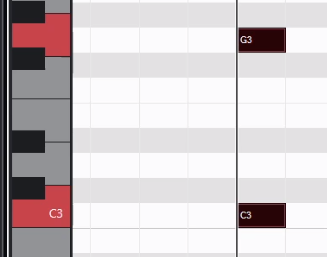
4度音程
例子
例1:1-2包含1,2两个音级,所以是二度
例2:3-7包含3,4,5,6,7五个音级,所以是五度
自然音程表
白键上的音程

| 音程 | 半音数 |
| 纯一度 | 0 |
| 小二度 | 1 |
| 大二度 | 2 |
| 小三度 | 3 |
| 大三度 | 4 |
| 纯四度 | 5 |
| 增四度/减五度/三全音 | 6 |
| 纯五度 | 7 |
| 小六度 | 8 |
| 大六度 | 9 |
| 小七度 | 10 |
| 大七度 | 11 |
| 纯八度 | 12 |
下面有2组半音关系,所以有2个半音,就是大二度

E3到C3有4组半音关系,根据对照表,可以知道是大三度
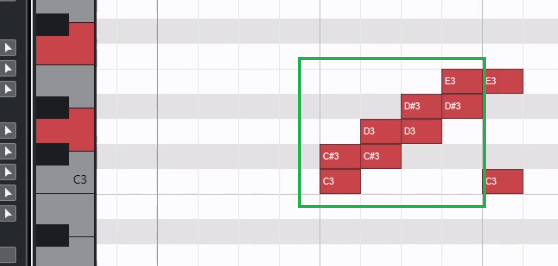
踩坑
请问E3和C#3是几度?
这个其实是不确定的,算是错误的题,乐理考试里面的坑,要看是升1还是降2,这种题干没有说明哪个低音到哪个高音。

正确的问法是:请问C#3到E3在Cubase中是几度音程关系?这种题干有说明哪个低音到哪个高音。
第一步,先出结论,这个是一个三度音程
第二步,计算大小增减,数半音
三组半音,所以是小三度

口诀
口诀1:倍减-减-小-大-增-倍增
口诀2:倍减-减-纯-增-倍增(比如以纯6度为开始,左边是以一个半音数进行递减,右边是以一个半音数进行递增!)
题目
C3到G3是几度?
是纯五度。

C3到A#3是几度?
是增六度。因为包含6个白键+1个半音,根据口诀2可以知道。
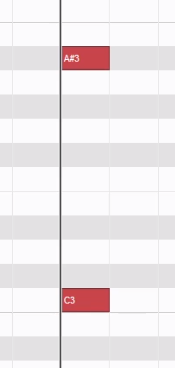
大小调体系
大调音阶:主音向上按照“全全半全全 全半”的音阶关系排列
小调音阶:主音向上按照“全半全全半全全”的音阶关系排列
自然大调音阶:CDEFGAB、1234567(C大调)
自然小调音阶:1 2 b3 4 5 b6 b7(C小调)
快速判断是大调还是小调的口诀
大调音阶:主音向上按照“全全半全全 全半”的音阶关系排列
小调音阶:主音向上按照“全半 全全半全全”的音阶关系排列
我发现都有全全半全全和全半,不过大调是全半在后面,小调是全半在前面,这样就可以很容易记住!
唱名法
以绝对音高为基础,任何调下永远不变
即1234567=CDEFGAB任何调下不变
固定调对于需要根据五线谱视奏的乐器更方便
例如提琴、古典钢琴等
首调唱名法
以相对音高为基础,不同调下唱名对应音名变化
先确定主音,再按照调式/音阶排列规律得到具体音名
例如G大调=以G为主音按照大调调式1234567排列得到 GABCDE F#
例如C Lydian(利底亚)=以C为主音按照Lydian音阶123 #4 567排列得到CDE F# GAB
首调更注重主音,以及其他音级和主音的关系
首调在即兴伴奏,流行/爵士即兴等情况下更方便
自然小调12 b3 45 b6 b7
为了减少变化音记号,用6712345来记忆,其中6为主音 简谱中常用此方法来记录小调
在自然大小调体系下,可能会更方便
如果涉及到自然大小调体系之外的调式,不建议再用此方法理解
个人理解
(我的理解就是你写出了一个C3为根音的C3大调,那么D3大调,其实就是把C3大调的midi全选后,然后Alt长按,拖动,复制到右边,然后用电脑中的向上或向下键,让midi整体向上移动,让根音变成D3,这样音程关系不变,就变成D3大调了)
常见调式、音阶
伊奥尼亚(Ionian):1 2 3 4 5 6 7------大调
多利亚(Dorian):1 2 b3 4 5 6 b7
弗利几亚(Phrygian):1 b2 b3 4 5 b6 b7
利底亚(Lydian):1 2 3 #4 5 6 7
混合利底亚(MixoLydian ):1 2 3 4 5 6 b7
爱奥尼亚( Aeolian ):1 2 b3 4 5 b6 b7------小调
洛克里亚( Iocrian ):1 b2 b3 4 b5 b6 b7
布鲁斯音阶( Blues ):1 b3 4 #4 5 b7
全音阶( diatonic ):1 2 3 #4 #5 #6
半音阶( chromatic scale):1 #1 2 #2 3 4 #4 5 #5 6 #6 7
调式、调性
调式+主音=调性
例1:调式=大调音阶、主音=C;调性=C大调
例2:调式=小调音阶、主音=A;调性=a小调
大小调体系中,分别以12个音为主音,大调有12种调性、小调有12种调性、共24种调性
关系大小调
音阶、调号相同的一对大小调,叫做关系大小调 24种调性=12对关系大小调 例1:C调音阶包含C大调、a小调两种调性
比如下方的大调和小调中,出现的音都一样,只是排列顺序不一样。

快速找到一个大调的关系小调
比如G大调的关系小调,找G3形成小三度的音,就是E3(在原调中有这个音出现),然后就写出来了。
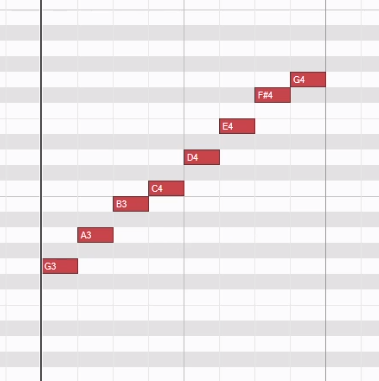

快速找到一个小调的关系大调
比如找到G小调的关系大调,就找G#3的小三度关系的音,是B3(在原调中有这个音出现)。


快速找到一个大调的同音名小调
坑
比如左边是C大调,右边是C小调。有些人找C大调的C小调,是先写出A2 B2 C3 D3 E3 F3 G3 A3,然后再去移动这个小调让根音和C3一样,这种方法不建议使用,因为即兴钢琴等情况下,是没有钢琴卷帘窗给你移动的(固定调唱名法)。
正确方法
C大调的C小调就是C大调的基础上降3,6,7级!这种可以快速写成某个大调的小调,我感觉这个方法很好用!
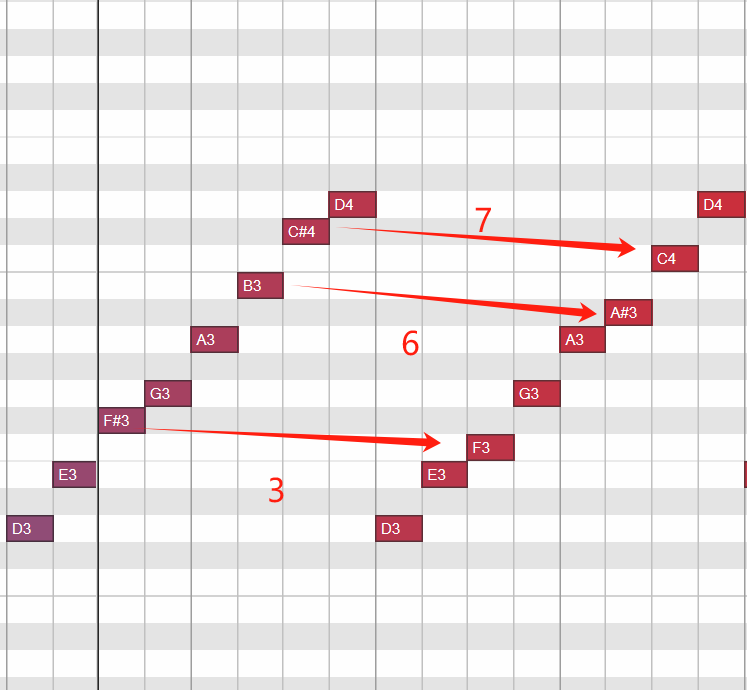
作业
作业1:写出PPT里面的所有的自然音程(和声音程),每一组两个
鼠标左键框选住2个音符,然后就可以在钢琴卷帘窗中数白键,检查自己的自然音程是否写得正确!同时我感觉Cubase中轨道视图和钢琴卷帘窗视图分开看,就已经很用了!
作业2:找出三组关系大小调并写在工程里面(C大调和a小调不算)
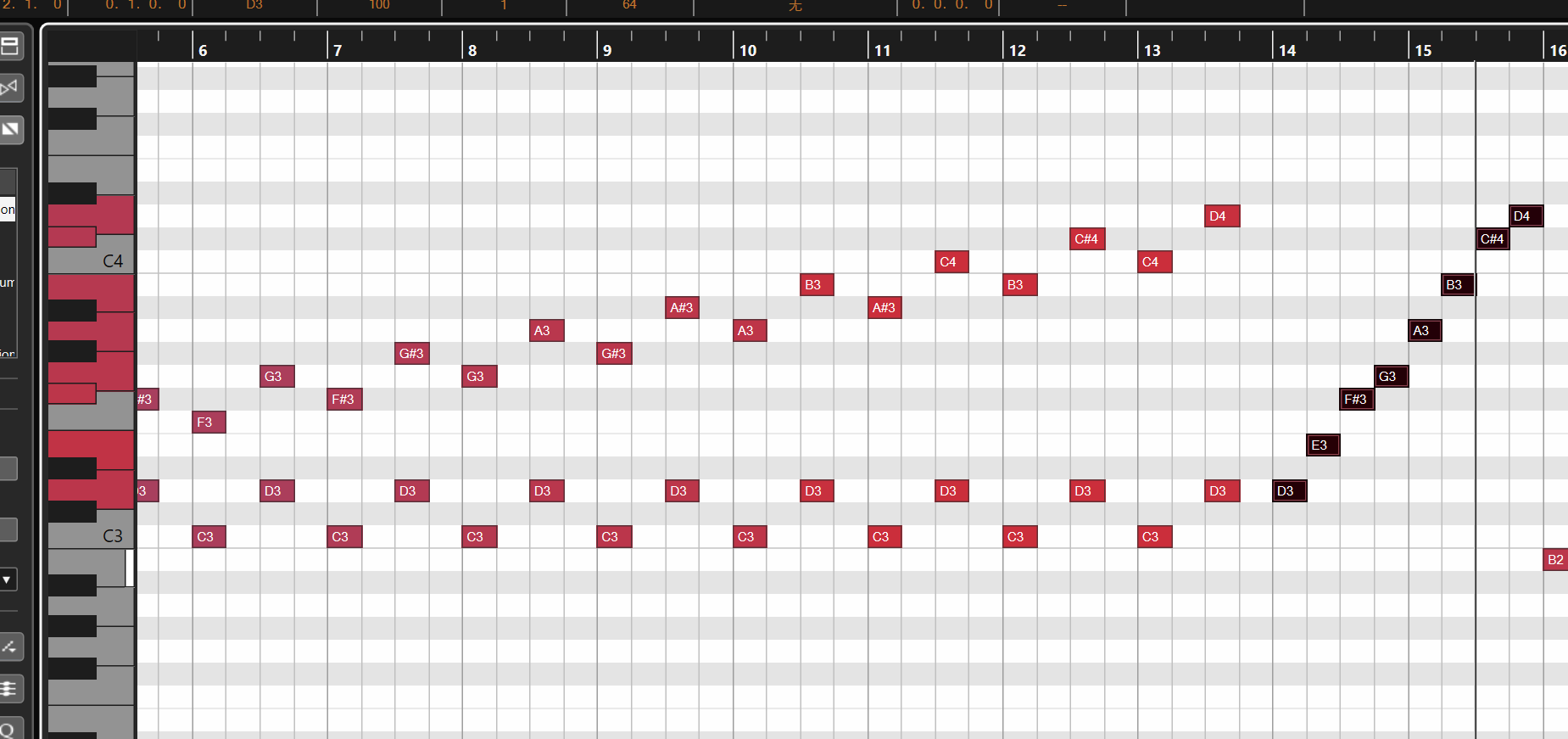
先写一个根音,比如D3,根据大调的口诀“全全半全全 全半”,写好大调,然后全选大调,然后长按Alt,拖动复制到右边的D3的小三度关系的B2(通过画“=”形,然后数几个=,就是几个半音,就是几组半音关系,3个组半音关系就是小三度),然后写出了B大调,然后改成B小调,用口诀“降3,6,7级”改成B小调。
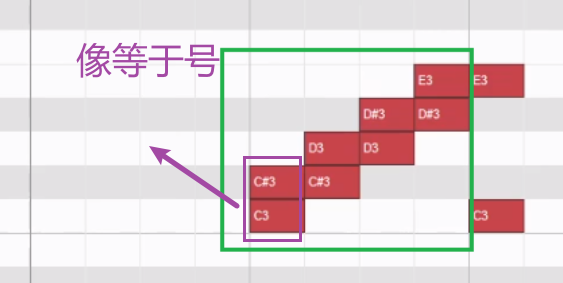
快速判断2个音之间的音程关系
或者可以理解成D3降一个小三度,就是向下移动3个等距离小格子(每个格子的高度就是一个半音的距离)的高度。

坑
大小调都8个音,自己之前粗心,少写了个音,以后写完作业,按口诀进行检查一下!

相关文章:

编曲学习:和声音程 调式体系 唱名法 调式调性
34届和声音程 调式体系 唱名法 调式调性https://app8epdhy0u9502.pc.xiaoe-tech.com/live_pc/l_65af994be4b064a8cb1c3a5f?course_idcourse_2XLKtQnQx9GrQHac7OPmHD9tqbv 34届独立音乐人编曲训练营https://app8epdhy0u9502.pc.xiaoe-tech.com/p/t_pc/course_pc_detail/camp_p…...

【大数据】Flink 架构(四):状态管理
《Flink 架构》系列(已完结),共包含以下 6 篇文章: Flink 架构(一):系统架构Flink 架构(二):数据传输Flink 架构(三):事件…...

执行rpm安装命令的时候抛出异常:rpmdb BDB0113 Thread/process
问题现象 错误:rpmdb: BDB0113 Thread/process 66126/140498505373504 failed: BDB1507 Thread died in Berkeley DB library 错误:db5 错误(-30973) 来自 dbenv->failchk:BDB0087 DB_RUNRECOVERY: Fatal error, run database recovery 错…...

Android 在WebView中加载H5传递图片
最近h5开发一个编译器,要在手机上显示,需要获取手机上的图片,使用webview不能直接到文件管理拿取,还需要对webview做处理,做个记录,方便以后使用; public ValueCallback<Uri[]> mUploadMe…...
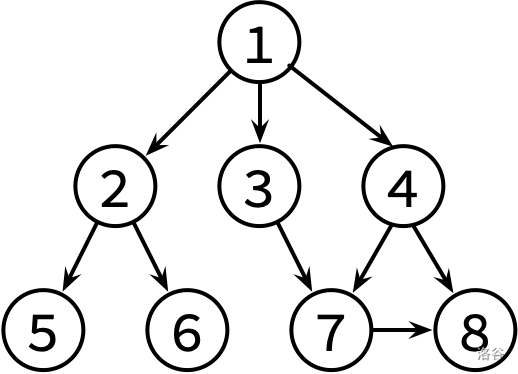
图的学习
图的基本概念和术语 图的定义:图是由顶点的有穷非空集合和顶点之间的边的集合组成的,G表示,V是图G中顶点的集合,E是图G中边的集合 无向图:任意两点的边都是无向边组成的图(无向边:(…...

空间数据分析入门POI与莫兰指数基础知识笔记
1. 空间分析与POI 1.1. 什么是POI POI是“Polnt of Information”的缩写,中文可以翻译为“信息点”。POI是地图上任何非地理意义的有意义的点,如商店、酒吧、加油站、医院、车站等。这些点通常包括名称、类别、经纬度和地址等基本信息。此外࿰…...
TortoiseSVN各版本汉化包下载
首先进入下载版本列表 1.下载地址:https://sourceforge.net/projects/tortoisesvn/files 2.选择自己版本进入 3.选择Language Packs进入,选择对应语言包下载。 4.在TortoiseSVN根目录下点击安装即可。 ...
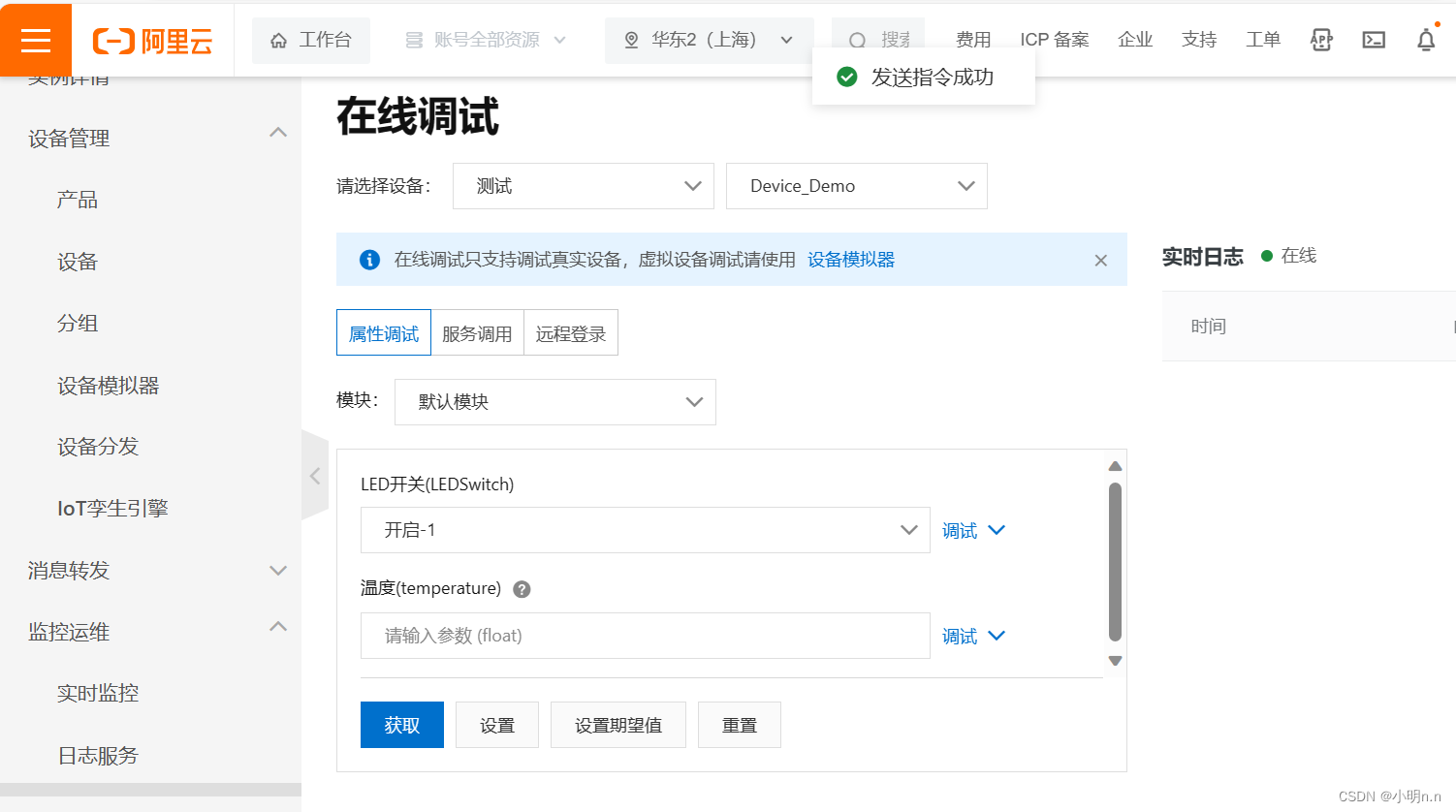
STM32连接阿里云物联网平台
文章目录 引言一、STM32连接阿里云物联网平台思路二、ESP8266烧录固件三、使用AT指令连接阿里云物联网平台四、STM32环形串口缓冲区驱动程序五、STM32连接阿里云驱动程序 引言 连续写了两篇关于阿里云连接的文章,都是使用Arduino ESP8266 & Arduino ESP32的方式…...
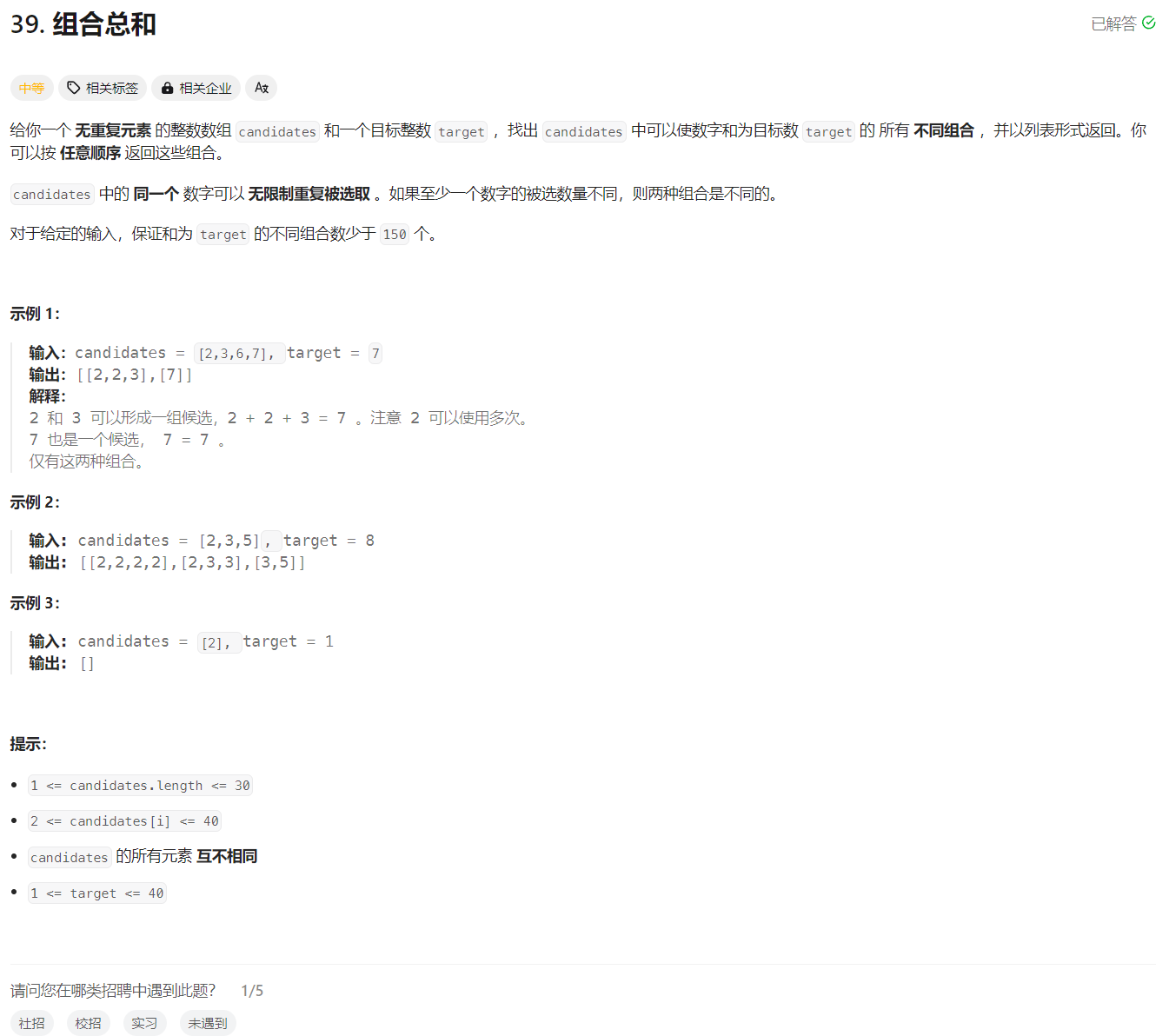
力扣hot100 组合总和 回溯 剪枝 组合
Problem: 39. 组合总和 文章目录 思路复杂度💖 Code 思路 复杂度 时间复杂度: O ( n ) O(n) O(n) 空间复杂度: O ( n ) O(n) O(n) 💖 Code class Solution{List<List<Integer>> res new ArrayList<>();int x;// 全局targetin…...
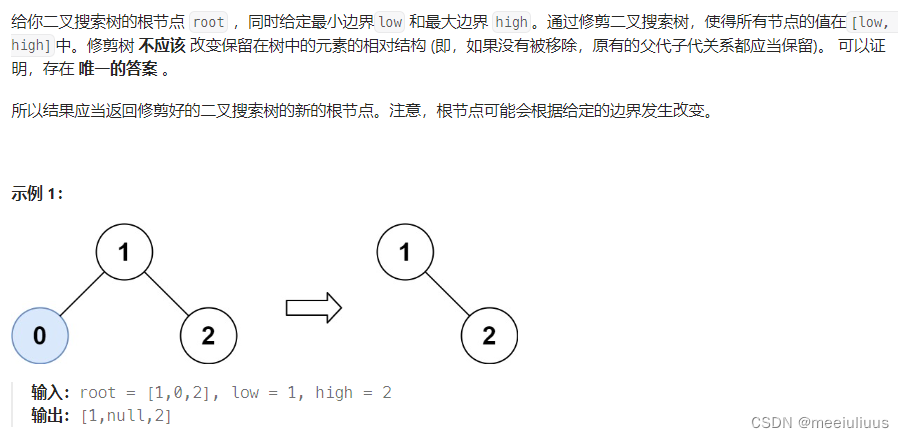
代码随想录 Leetcode669. 修剪二叉搜索树
题目: 代码(首刷看解析 2024年1月31日): class Solution { public:TreeNode* trimBST(TreeNode* root, int low, int high) {if (!root) return root;if (root->val < low) {TreeNode* node trimBST(root->right,low,high);return…...
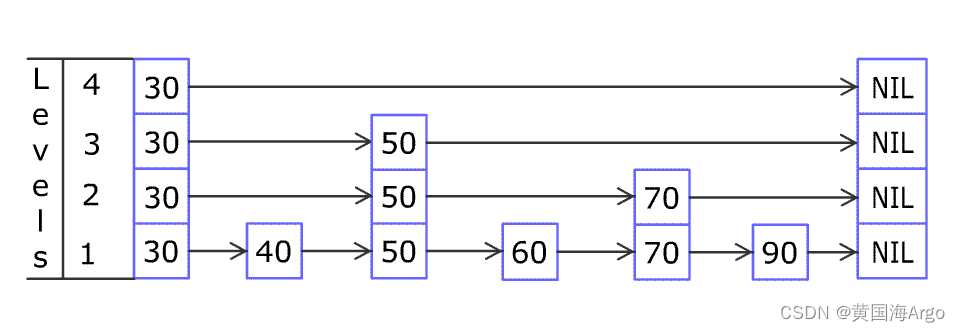
Redis系列-数据结构篇
数据结构 string(字符串) redis的字符串是动态字符串,类似于ArrayList,采用预分配冗余空间的方式减少内存的频繁分配。 struct SDS<T>{ T capacity; T len; byte flags; byte[] content; } 当字符串比较短时,…...
正则表达式(RE)
什么是正则表达式 正则表达式,又称规则表达式(Regular Expression)。正则表达式通常被用来检索、替换那些符合某个规则的文本 正则表达式的作用 验证数据的有效性替换文本内容从字符串中提取子字符串 匹配单个字符 字符功能.匹配任意1个…...

发布技术路线图!美国量子计算公司QuEra公开三年OKR
编辑丨慕一 编译/排版丨琳梦 卉可 深度好文:1100字丨8分钟阅读 近期,美国量子计算公司QuEra Computing宣布了一系列关于容错量子计算机的战略路线图,该路线图从2024年开始,最终目标是打造具有100纠错逻辑量子比特的系统。 在…...

Vue2:请求接口的两种方式axios和vue-resource
一、场景描述 前端和后端的交互,肯定是要发生接口调用的 这个时候,就要涉及前端如何向后端接口发送请求,获取数据 二、请求方式 1、axios方式(推荐) 这个方式本质就是ajax,底层就是对xhr(XMLHttpRequest)的封装 1、安装axios…...
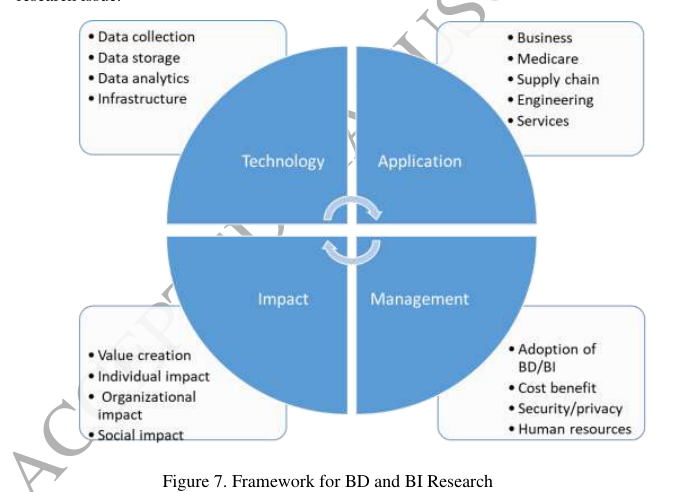
扩展学习|商业智能和大数据分析的研究前景(比对分析)
文献来源: Liang T P , Liu Y H .Research Landscape of Business Intelligence and Big Data analytics: A bibliometrics study[J].Expert Systems with Applications, 2018, 111(NOV.):2-10.DOI:10.1016/j.eswa.2018.05.018. 信息和通信技术的快速发展导致了数字…...

『Docker入门指南』- 详细安装与配置教程,助你起航容器化世界!
引言 在探索云计算和自动化部署的时代,Docker以其独特的容器化技术站在了风口浪尖。如果你期待着无缝地将你的应用从一个环境迁移到另一个环境,那么Docker无疑是你的得力助手。但首先,我们得学会如何正确地安装和配置Docker。这篇文章将详细…...

如何提高http连接成功率?
问题 丢包、错包、乱包 高延迟 响应数据回来时间长,甚至大于客户端等待时间 带宽小 每次能够通信的内容较少,数据包越大受影响可能越大 网络断续 网络经常断开又连接 优化处理 采用TCP协议、实现长连接,采用长连接池,节省…...

Elasticsearch 中使用MustNot等同于不等于遇到的坑
1、在写关键词推荐时,需要把当前文章过滤掉,不能再推荐自己的文章,所以再es中需要用到 MustNot属性查询 /// <summary> /// 服务中心es检索 /// </summary> /// <param name="input"></param> /// <returns></…...

嵌入式工程师day15(链表)
内存管理 一.内存管理: 1.malloc void *malloc(size_t size); 功能: 申请堆区空间 参数: size:申请堆区空间的大小 返回值: 返回获得的空间的首地址 失败返回NULL 2.free void free(void *ptr); 功能: 释放…...
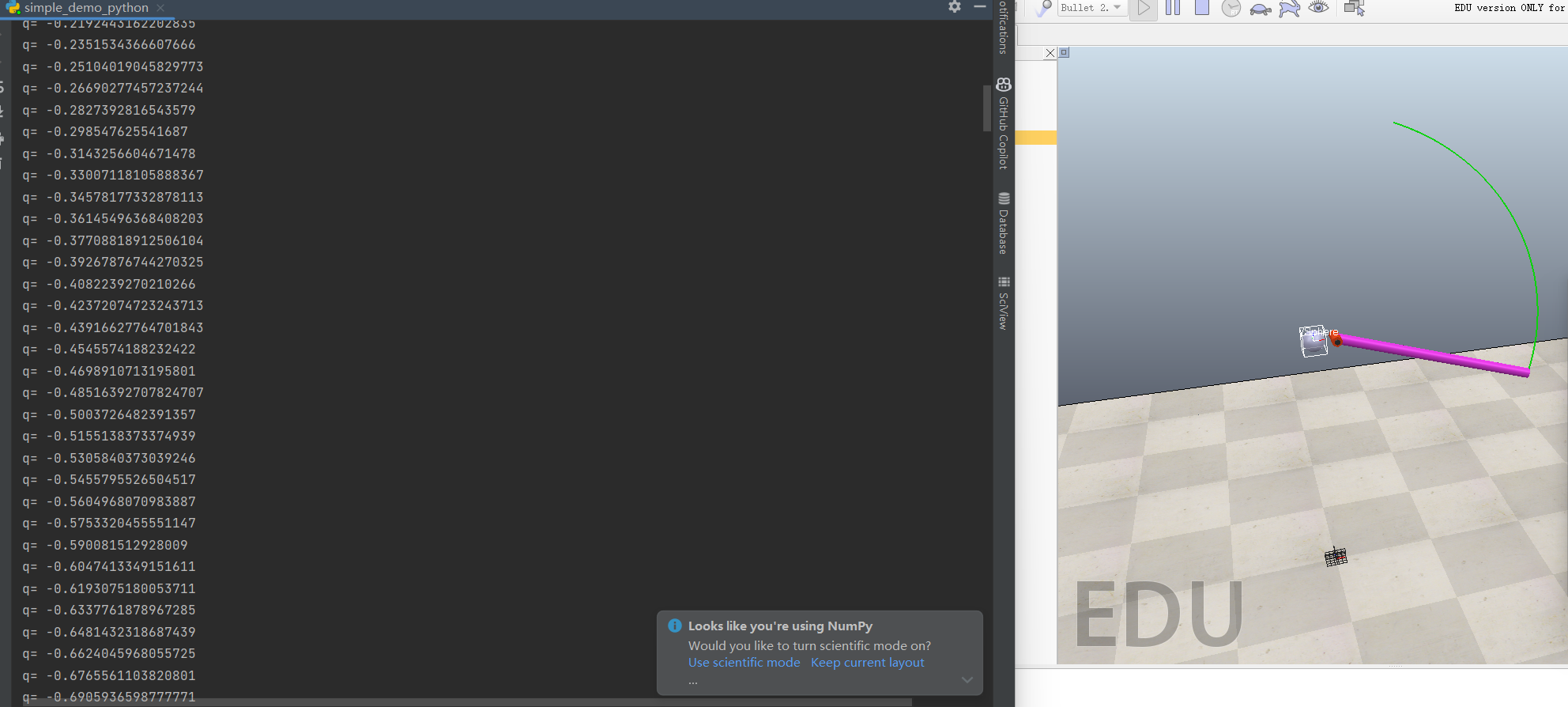
Coppeliasim倒立摆demo
首先需要将使用Python远程控制的文件导入到文件夹,核心是深蓝色的三个文件。 本版本为4.70,其文件所在位置如下图所示,需要注意的是,目前不支持Ubuntu22的远程api: 双击Sphere这一行的灰色文件,可以看到远程…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

