大数据期望最大化(EM)算法:从理论到实战全解析
文章目录
- 大数据期望最大化(EM)算法:从理论到实战全解析
- 一、引言
- 概率模型与隐变量
- 极大似然估计(MLE)
- Jensen不等式
- 二、基础数学原理
- 条件概率与联合概率
- 似然函数
- Kullback-Leibler散度
- 贝叶斯推断
- 三、EM算法的核心思想
- 期望(E)步骤
- 最大化(M)步骤
- Q函数与辅助函数
- 收敛性
- 四、EM算法与高斯混合模型(GMM)
- 高斯混合模型的定义
- 分量权重
- E步骤在GMM中的应用
- M步骤在GMM中的应用
- 五、实战案例
- 定义:目标
- 定义:输入和输出
- 实现步骤
- 结果解释
- 六、总结
大数据期望最大化(EM)算法:从理论到实战全解析
本文深入探讨了大数据期望最大化(EM)算法的原理、数学基础和应用。通过详尽的定义和具体例子,文章阐释了EM算法在高斯混合模型(GMM)中的应用,并通过Python和PyTorch代码实现进行了实战演示。
一、引言
期望最大化算法(Expectation-Maximization Algorithm,简称EM算法)是一种迭代优化算法,主要用于估计含有隐变量(latent variables)的概率模型参数。它在机器学习和统计学中有着广泛的应用,包括但不限于高斯混合模型(Gaussian Mixture Model, GMM)、隐马尔可夫模型(Hidden Markov Model, HMM)以及各种聚类和分类问题。
概率模型与隐变量
概率模型是一种用数学表示的数据生成过程。在统计学和机器学习中,一个概率模型通常用来描述观测数据(observable data)和潜在结构(latent structure)之间的关系。
- 例子:假设我们有一个数据集,包含了一群人的身高和体重。一个简单的概率模型可能假设身高和体重都符合正态分布。
**隐变量(Latent Variables)**是指那些不能直接观测到,但会影响到观测数据的变量。在包含隐变量的概率模型中,通常更难以进行参数估计。
- 例子:在推断一群人是否喜欢运动的情况下,我们可能能观测到他们的身高和体重,但“是否喜欢运动”这一隐变量是无法直接观测的。
极大似然估计(MLE)
**极大似然估计(Maximum Likelihood Estimation, MLE)**是一种用于估计概率模型参数的方法。它通过寻找一组参数,使得给定观测数据出现的可能性(即似然函数)最大化。
- 例子:在一个硬币投掷实验中,观测到了10次正面和15次反面,MLE会寻找一个参数(硬币正面朝上的概率),使得观测到这样的数据最有可能。
Jensen不等式
Jensen不等式是凸优化理论中的一个基本不等式,常用于证明EM算法的收敛性。简单地说,Jensen不等式表明对于一个凸函数,函数在凸组合上的值不会大于凸组合中各点值的平均。

二、基础数学原理
在理解EM算法的工作机制之前,我们需要掌握一些关键的数学概念和原理。这些原理不仅形成了EM算法的数学基础,而且也有助于我们理解算法的收敛性和效率。
条件概率与联合概率

似然函数

Kullback-Leibler散度

贝叶斯推断
贝叶斯推断是一种基于贝叶斯定理的参数估计和模型选择方法。它使用先验概率、似然函数和证据(或归一化因子)来计算参数的后验概率。
- 例子:在垃圾邮件分类中,贝叶斯推断可以用于更新垃圾邮件(或非垃圾邮件)的概率,每当用户标记一个新邮件时。
这些数学原理为我们提供了理解EM算法所需的坚实基础。通过了解这些概念,我们可以更深入地探讨EM算法如何进行参数估计,特别是在存在隐变量的复杂模型中。
三、EM算法的核心思想

EM算法的主要目的是找到含有隐变量的概率模型的参数估计。这一目标在直接应用极大似然估计(MLE)困难或不可行时尤为重要。EM算法通过交替执行两个步骤来实现这一目标:期望(E)步骤和最大化(M)步骤。
期望(E)步骤
期望步骤(Expectation step)涉及计算隐变量给定观测数据和当前参数估计的条件期望。这通常用于构建一个函数,称为Q函数,来近似目标函数(通常是似然函数)。
- 例子:在高斯混合模型中,期望步骤涉及计算每个观测数据点属于各个高斯分布的条件概率,这些概率也称为后验概率。
最大化(M)步骤
最大化步骤(Maximization step)则是在给定Q函数的情况下,寻找能使Q函数最大化的参数值。
- 例子:继续上面的高斯混合模型例子,最大化步骤涉及调整每个高斯分布的均值和方差,以最大化由期望步骤得到的Q函数。
Q函数与辅助函数
Q函数是EM算法中的一个核心概念,用于近似目标函数(如似然函数)。Q函数通常依赖于观测数据、隐变量和模型参数。
- 例子:在高斯混合模型的EM算法中,Q函数基于观测数据和各个高斯分布的后验概率来定义。
**辅助函数(Auxiliary Function)**是EM算法的一个重要组成部分,用于保证算法收敛。通过最大化辅助函数,我们间接地最大化了似然函数。
- 例子:在一些文本分类问题中,辅助函数可以通过拉格朗日乘数法来构建,以简化最大化问题。
收敛性
在EM算法中,由于使用了Jensen不等式和辅助函数,算法保证会收敛到局部最大值。
- 例子:在实施高斯混合模型的EM算法后,你会发现每次迭代都会导致似然函数的值增加(或保持不变),直到达到局部最大值。
通过深入探讨这些核心概念和步骤,我们能更全面地理解EM算法是如何工作的,以及为什么它在处理含有隐变量的复杂概率模型时如此有效。
四、EM算法与高斯混合模型(GMM)
高斯混合模型(Gaussian Mixture Model,GMM)是一种使用高斯概率密度函数(pdf)为基础构建的概率模型。它是EM算法应用的一个典型例子,尤其是当我们要对数据进行聚类或者密度估计时。
高斯混合模型的定义
高斯混合模型是由多个高斯分布组成的。每一个高斯分布称为一个分量(component),并且每一个分量都有其自己的均值((\mu))和方差((\sigma^2))。
- 例子:假设一个数据集呈现出两个明显不同的簇。一个高斯混合模型可能会用两个高斯分布来描述这两个簇,每个分布有自己的均值和方差。
分量权重
每个高斯分量在模型中都有一个权重((\pi_k)),这个权重描述了该分量对整个数据集的“重要性”。
- 例子:在一个由两个高斯分布组成的GMM中,如果一个分布的权重为0.7,另一个为0.3,这意味着第一个分布对整个模型的影响较大。
E步骤在GMM中的应用
在GMM中的E步骤,我们计算数据点对每个高斯分量的后验概率,即给定数据点,它来自某个特定分量的概率。
- 例子:假设一个数据点(x),在E步骤中,我们计算它来自GMM中每个高斯分量的后验概率。
# 使用Python和PyTorch计算后验概率
import torch
from torch.distributions import MultivariateNormal# 假设有两个分量
means = [torch.tensor([0.0]), torch.tensor([5.0])]
variances = [torch.tensor([1.0]), torch.tensor([2.0])]
weights = [0.6, 0.4]# 数据点
x = torch.tensor([1.0])# 计算后验概率
posterior_probabilities = []
for i in range(2):normal_distribution = MultivariateNormal(means[i], torch.eye(1) * variances[i])posterior_probabilities.append(weights[i] * torch.exp(normal_distribution.log_prob(x)))# 归一化
sum_probs = sum(posterior_probabilities)
posterior_probabilities = [prob / sum_probs for prob in posterior_probabilities]print("后验概率:", posterior_probabilities)
M步骤在GMM中的应用
在M步骤中,我们根据E步骤计算出的后验概率来更新每个高斯分量的参数(均值和方差)。
- 例子:假设从E步骤中获得了数据点对于两个高斯分量的后验概率,我们会用这些后验概率来加权地更新均值和方差。
通过详细地探讨高斯混合模型和它与EM算法的关联,我们更深入地理解了这一复杂模型是如何工作的,以及EM算法在其中扮演了什么角色。这不仅有助于我们理解算法的数学基础,还为实际应用提供了实用的见解。
五、实战案例
在实战案例中,我们将使用Python和PyTorch来实现一个简单的高斯混合模型(GMM)以展示EM算法的应用。
定义:目标
我们的目标是对一维数据进行聚类。我们将使用两个高斯分量(也就是说,K=2)。
- 例子:假设我们有一个一维数据集,其中包含两个簇。我们希望使用GMM模型找到这两个簇的参数(均值和方差)。
定义:输入和输出
- 输入:一维数据数组
- 输出:两个高斯分量的参数(均值和方差)以及它们的权重。
实现步骤
- 初始化参数:为均值、方差和权重设置初始值。
- E步骤:计算数据点属于每个分量的后验概率。
- M步骤:使用后验概率更新均值、方差和权重。
- 收敛检查:检查参数是否收敛。如果没有,则返回第2步。
# Python和PyTorch代码实现
import torch
from torch.distributions import Normal# 初始化参数
means = torch.tensor([0.0, 5.0])
variances = torch.tensor([1.0, 1.0])
weights = torch.tensor([0.5, 0.5])# 假设的一维数据集
data = torch.cat((torch.randn(100) * 1.5, torch.randn(100) * 0.5 + 5))# EM算法实现
for iteration in range(100):# E步骤posterior_probabilities = []for i in range(2):normal_distribution = Normal(means[i], torch.sqrt(variances[i]))posterior_probabilities.append(weights[i] * torch.exp(normal_distribution.log_prob(data)))# 归一化sum_probs = torch.stack(posterior_probabilities).sum(0)posterior_probabilities = [prob / sum_probs for prob in posterior_probabilities]# M步骤for i in range(2):responsibility = posterior_probabilities[i]means[i] = torch.sum(responsibility * data) / torch.sum(responsibility)variances[i] = torch.sum(responsibility * (data - means[i])**2) / torch.sum(responsibility)weights[i] = torch.mean(responsibility)# 输出当前参数print(f"Iteration {iteration+1}: Means = {means}, Variances = {variances}, Weights = {weights}")
结果解释
在运行以上代码后,你将看到均值、方差和权重的参数在每次迭代后都会更新。当这些参数不再显著变化时,我们可以认为算法已经收敛。
- 输入:一维数据集,包含两个簇。
- 输出:每次迭代后的均值、方差和权重。
通过这个实战案例,我们不仅演示了如何在PyTorch中实现EM算法,并且通过具体的代码示例深入理解了算法的每一个步骤。这样的内容安排旨在满足你对于概念丰富、充满细节和定义完整的需求。
六、总结
经过详尽的理论分析和实战示例,我们对期望最大化(EM)算法有了更全面的了解。从基础数学原理到具体的实现和应用,EM算法展示了其在统计模型参数估计中的强大能力,特别是当我们面临缺失或隐含数据时。
- 概率模型的选择:虽然我们在实战中使用了高斯混合模型(GMM),但EM算法并不仅限于此。事实上,它可以应用于任何满足特定条件的概率模型,这一点在研究和应用更为复杂的数据结构时尤为重要。
- 初始化的重要性:本文提到了参数的初始选择,但实际应用中应更加小心。糟糕的初始化可能导致算法陷入局部最优,从而影响模型性能。
- 收敛性和效率:尽管EM算法通常能保证收敛,但收敛速度可能是一个问题,特别是在高维数据和复杂模型中。这一点可能会促使我们寻找更有效的优化算法或者采用分布式计算。
- 模型解释性与复杂性的权衡:EM算法能够估计复杂模型的参数,但这种复杂性可能会导致模型解释性降低。在实际应用中,我们需要仔细考虑这种权衡。
- 算法的泛化能力:EM算法不仅用于聚类问题,在自然语言处理、计算生物学等多个领域也有广泛应用。了解其核心思想和工作机制能为处理不同类型的数据问题提供有力的工具。
法通常能保证收敛,但收敛速度可能是一个问题,特别是在高维数据和复杂模型中。这一点可能会促使我们寻找更有效的优化算法或者采用分布式计算。
4. 模型解释性与复杂性的权衡:EM算法能够估计复杂模型的参数,但这种复杂性可能会导致模型解释性降低。在实际应用中,我们需要仔细考虑这种权衡。
5. 算法的泛化能力:EM算法不仅用于聚类问题,在自然语言处理、计算生物学等多个领域也有广泛应用。了解其核心思想和工作机制能为处理不同类型的数据问题提供有力的工具。
通过深入地探讨这些技术洞见,我们不仅加深了对EM算法核心概念和工作机制的理解,还能更好地将这一算法应用到各种实际问题中。希望这篇文章能进一步促进你对于复杂概率模型和期望最大化算法的理解,也希望你能在自己的项目或研究中找到这些信息的实际应用。最近一段时间发现自己在一些新的技术框架领域仍然不够熟练,集成不够专业,本人也在不断学习进步,打破思维认知,才能有质的的飞跃与进步,不破不立。
相关文章:

大数据期望最大化(EM)算法:从理论到实战全解析
文章目录 大数据期望最大化(EM)算法:从理论到实战全解析一、引言概率模型与隐变量极大似然估计(MLE)Jensen不等式 二、基础数学原理条件概率与联合概率似然函数Kullback-Leibler散度贝叶斯推断 三、EM算法的核心思想期…...
【鸿蒙】大模型对话应用(二):对话界面设计与实现
Demo介绍 本demo对接阿里云和百度的大模型API,实现一个简单的对话应用。 DecEco Studio版本:DevEco Studio 3.1.1 Release HarmonyOS SDK版本:API9 关键点:ArkTS、ArkUI、UIAbility、网络http请求、列表布局、层叠布局 对话页…...

MySQL 导入数据
我们可以将已有的数据导入到MySQL数据库中,下面是几种方式: 1、mysql 命令导入 使用 mysql 命令导入语法格式为: mysql -u用户名 -p密码 < 要导入的数据库数据(shulanxt.sql) 实例: # mysql -uroot -p123456 < …...

探索数字经济:从基础到前沿的奇妙旅程
新一轮技术革命方兴未艾,特别是以人工智能、大数据、物联网等为代表的数字技术革命,催生了一系列新技术、新产业、新模式,深刻改变着世界经济面貌。数字经济已成为重组全球要素资源、重塑全球经济结构、改变全球竞争格局的关键力量。预估到20…...
】如何在 Windows 操作系统上设置 Design Space Explorer II 远程 SSH 场)
【INTEL(ALTERA)】如何在 Windows 操作系统上设置 Design Space Explorer II 远程 SSH 场
说明 从英特尔 Quartus Prime Pro Edition 软件 22.1 版本开始,您可以选择使用 Windows OpenSSH 服务器设置 Design Space Explorer II (DSE II)。 解决方法 1.让 DSE II 与 OpenSSH 协同工作的第一步是 安装 OpenSSH。应在远程主机上安装 Op…...

Python编程-使用urllib进行网络爬虫常用内容梳理
Python编程-使用urllib进行网络爬虫常用内容梳理 使用urllib库进行基础网络请求 使用request发起网络请求 from urllib import request from http.client import HTTPResponseresponse: HTTPResponse request.urlopen(url"http://pkc/vul/sqli/sqli_str.php") pr…...
01 Redis的特性+下载安装启动+Redis自动启动+客户端连接
1.1 NoSQL NoSQL(“non-relational”, “Not Only SQL”),泛指非关系型的数据库。 键值存储数据库 : 就像 Map 一样的 key-value 对。如Redis文档数据库 : NoSQL 与关系型数据的结合,最像关系…...

C++发起Https请求
Wininet库忽略Https证书 相信很多朋友使用C WINAPI开发的时候网络模块的时候遇到Https忽悠证书无效的情况下, 仍然希望获取结果下列代码便是忽略异常的Https CA证书,下面对原理进行简单的讲解首先, 需要设置Https忽略需要用到如下结果函数与参数Interne…...
哪款笔记软件支持电脑和手机互通数据?
上班族在日常工作中,随手记录工作笔记已成为司空见惯的场景。例如:从快节奏的会议记录到灵感迸发的创意;跟踪项目进展,记录每个阶段的成果、问题和下一步计划;记录、更新工作任务清单等,工作笔记承载了职场…...
部署PXE高效批量网络装机
部署PXE高效批量网络装机 因在Cisco3850核心交换机中已开启DHCP 服务,因此不需要在配置DHCP服务。如果您的网络环境中也已有DHCP服务,也不用再配置DHCP服务了,直接部署PXE相关服务即可。 找一台linux系统的服务器,这本次试验用的是…...
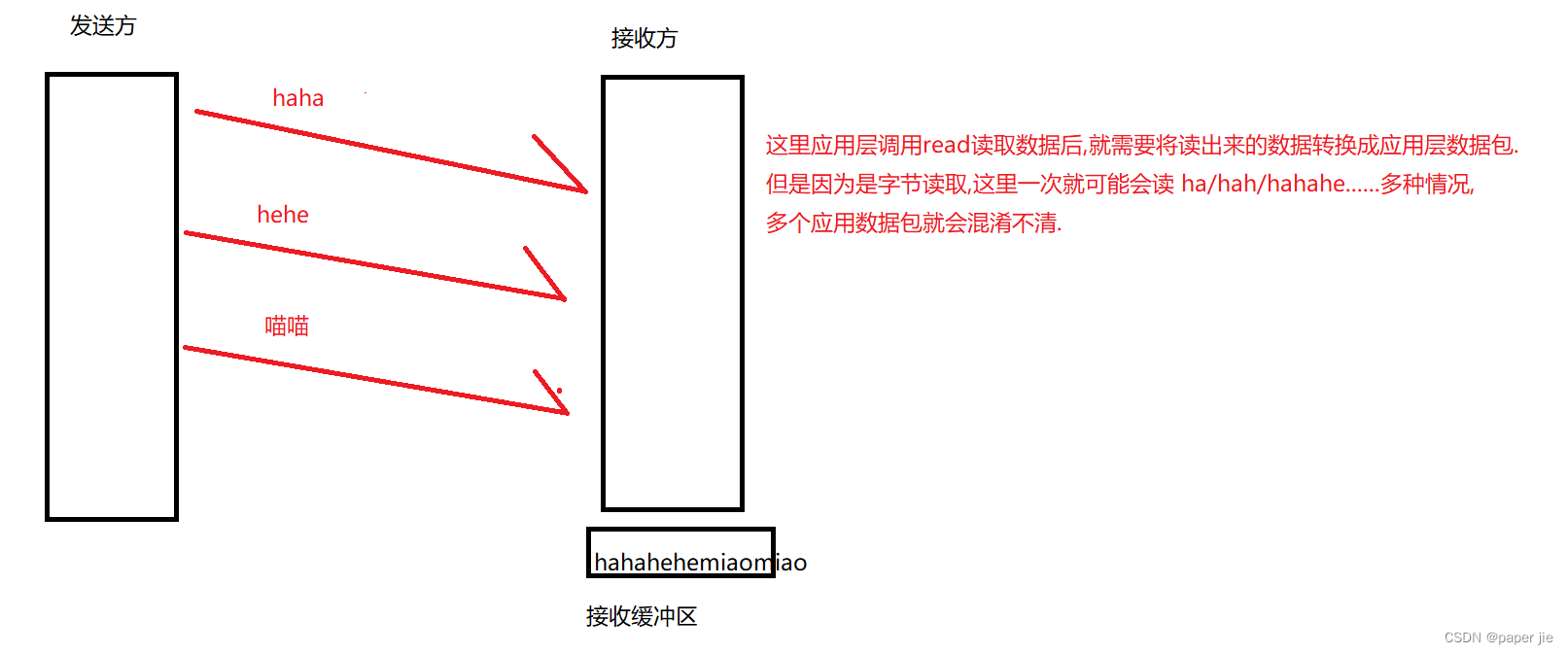
【JavaEE】UDP协议与TCP协议
作者主页:paper jie_博客 本文作者:大家好,我是paper jie,感谢你阅读本文,欢迎一建三连哦。 本文于《JavaEE》专栏,本专栏是针对于大学生,编程小白精心打造的。笔者用重金(时间和精力)打造&…...

Leetcode—1828. 统计一个圆中点的数目【中等】
2024每日刷题(一零五) Leetcode—1828. 统计一个圆中点的数目 实现代码 class Solution { public:vector<int> countPoints(vector<vector<int>>& points, vector<vector<int>>& queries) {vector<int> a…...
)
新概念英语第二册(47)
New words and expressions】生词和短语(9) thirsty adj. 贪杯的 ghost n. 鬼魂 haunt v. (鬼)来访,闹鬼 block …...
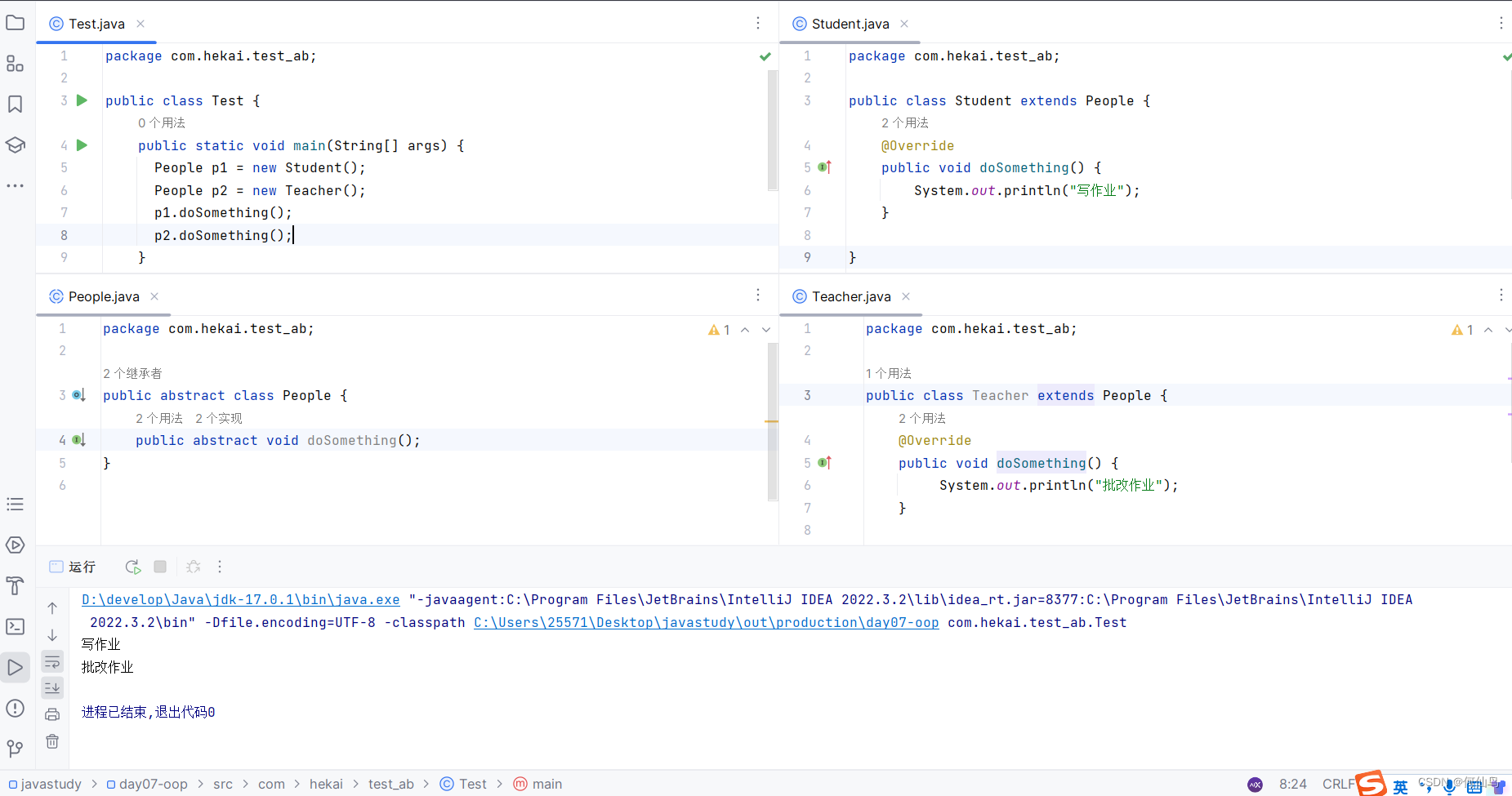
抽象类(Java)、模板方法设计模式
一、概念 在Java中有abstract关键字,就是抽象的意思,可用来修饰类和成员方法。 用abstract来修饰类,那这个类就是抽象类;修饰方法,那这个方法就是抽象方法。 修饰符 abstract class 类名{修饰符 abstract 返回值类型…...

【Delphi】IDE 工具栏错乱恢复
由于经常会在4K和2K显示器上切换Delphi开发环境(IDE),导致IDE工具栏错乱,咋样设置都无法恢复,后来看到红鱼儿的博客,说是通过操作注册表的方法,能解决,试了一下,果真好用,非常感谢分…...
)
自动化报告的前奏|使用python-pptx操作PPT(一)
自动化报告先从python-pptx开始 文章目录 1 python-pptx的基础属性1.1 新建幻灯片1.1.1 幻灯片布局的样式1.1.2 修改pptx模版大小1.1.3 指定模版生成1.1.4 创建幻灯片背景1.1.5 创建幻灯片备注信息1.1.6 设置幻灯片标题1.2 一些ppt元素/组件1.2.1 特殊符号1.2.2 placeholders1.…...

2024美赛数学建模D题思路+代码
文章目录 1 赛题思路2 美赛比赛日期和时间3 赛题类型4 美赛常见数模问题5 建模资料 1 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 2 美赛比赛日期和时间 比赛开始时间:北京时间2024年2月2日(周五ÿ…...
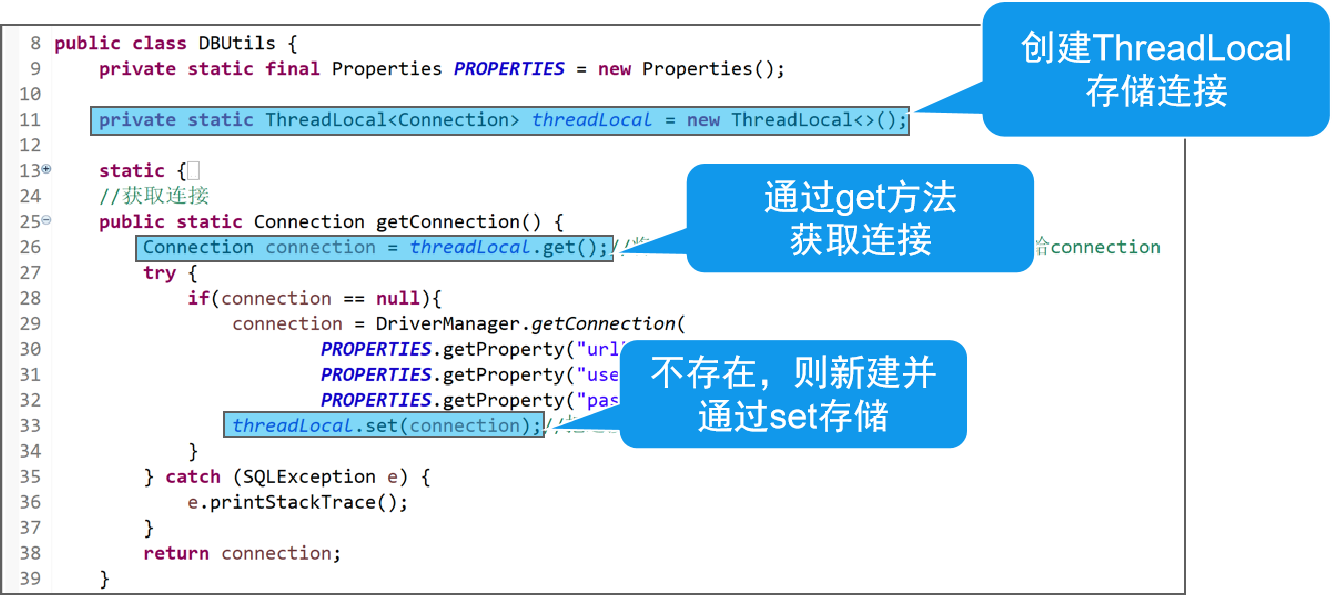
JDBC 结构优化2
JDBC 结构优化2 文章目录 JDBC 结构优化2结构优化2 - ATM系统(存,取,转,查)1 Service2 事务3 ThreadLocal4 事务的封装 结构优化2 - ATM系统(存,取,转,查) 1 Service 什么是业务? 代表用户完成的一个业务功能,可以由一个或多个DAO的调用组成。软件所提供的一个功…...

大模型相关术语
AGI(Artificial General Intelligence) 指通用人工智能,专注于研制像人一样思考、像人一样从事多种用途的机器。它与一般的特定领域智能(如机器视觉、语音识别等)相区分。 AIGC(AI-Generated Content&…...

数据库之九 流程控制、存储过程和函数
【零】数据准备 【1】创建用户信息表 (1)创建表 id:编号name:用户名sex:性别,默认男balance:余额register_time:注册时间 drop table if exists user; create table user( id in…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...
