88.合并两个有序数组
88.合并两个有序数组
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
**注意:**最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
解释:需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
解释:需要合并 [1] 和 [] 。
合并结果是 [1] 。
示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1
输出:[1]
解释:需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。
提示:
nums1.length == m + nnums2.length == n0 <= m, n <= 2001 <= m + n <= 200-109 <= nums1[i], nums2[j] <= 109
**进阶:**你可以设计实现一个时间复杂度为 O(m + n) 的算法解决此问题吗?
思路:
public class Problem_0088_MergeSortedArray {public void merge(int[] nums1, int m, int[] nums2, int n) {int index = nums1.length;while (m > 0 && n > 0) {if (nums1[m - 1] >= nums2[n - 1]) {nums1[--index] = nums1[--m];} else {nums1[--index] = nums2[--n];}}while (m > 0) {nums1[--index] = nums1[--m];}while (n > 0) {nums1[--index] = nums2[--n];}}
}
相关文章:

88.合并两个有序数组
88.合并两个有序数组 给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。 **注意:**最…...

python查询xml类别
第一章 导包 import os from xml.etree.ElementTree import ElementTree第二章 存储类别 # 定义一个空集合用于存储类别 classes set()第三章 遍历所有XML文件 # 遍历指定目录下的所有XML文件 for filename in os.listdir(/home/li/PycharmProjects/Annotations):if filena…...

nginx配置及性能优化
1. 请简述nginx的工作原理? Nginx的工作原理基于事件驱动模型和异步非阻塞I/O处理机制。 具体来说,Nginx接收到客户端的请求后,会将该请求映射到配置文件中指定的location block。这个过程中,Nginx本身并不执行实际的工作&#…...
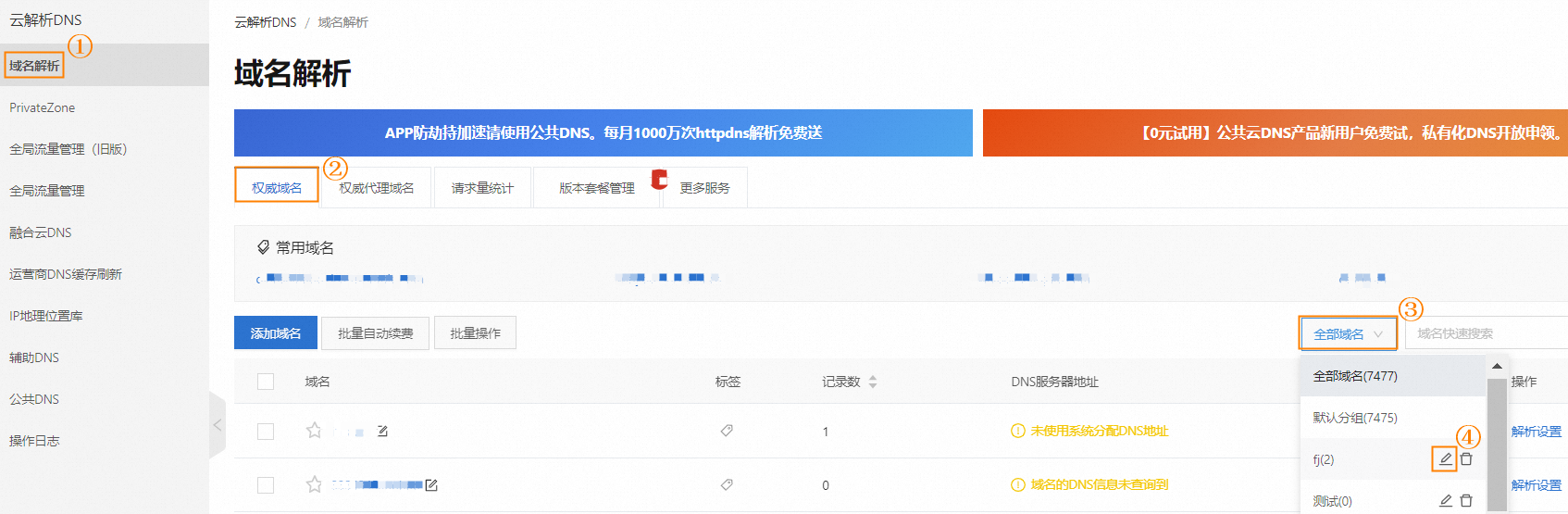
阿里云如何找回域名,进行添加或删除?
权威域名管理介绍说明,包含添加域名、删除域名、找回域名、域名分组等操作介绍。 一、添加域名 非阿里云注册域名或子域名如需使用云解析DNS,需要通过添加域名功能,将主域名或子域名添加到云解析控制台,才可以启用域名解析服务。…...
机器学习 低代码 ML:PyCaret 的使用
✅作者简介:人工智能专业本科在读,喜欢计算机与编程,写博客记录自己的学习历程。 🍎个人主页:小嗷犬的个人主页 🍊个人网站:小嗷犬的技术小站 🥭个人信条:为天地立心&…...
前端入门第二天
目录 一、列表、表格、表单 二、列表(布局内容排列整齐的区域) 1.无序列表(不规定顺序) 2.有序列表(规定顺序) 3.定义列表(一个标题多个分类) 三、表格 1.表格结构标签 2.合并…...

Django实现富文本编辑器Ckeditor5图片上传功能
上一章我们已经为我们的博客继承了富文本编辑器Ckeditor5,虽然已经可以对文字进行排版处理,虽然已经可以通过插入图片的url地址来插入图片,但还无法通过本地上传图片,那么我们这个富文本编辑器就是不完整的,这一章我们将实现上传图片功能! Ckeditor5图片上传采用的是…...

【C语言】epoll_wait / select
一、epoll_wait和select对比 1. 阻塞和非阻塞 在Linux C语言中进行socket编程时,epoll_wait 和 select 都是用于多路I/O复用的系统调用,但是它们的行为可以设置为阻塞和非阻塞模式,这取决于调用它们时所使用的参数。 让我们分别看看 epoll…...
Java 数据抓取
大家好我是苏麟 , 今天聊聊数据抓取 . 大家合理使用 注意,爬虫技术不能滥用,干万不要给别人的系统造成压力、不要侵犯他人权益! 数据抓取 实质上就是java程序模拟浏览器进行目标网站的访问,无论是请求目标服务器的接口还是请求目标网页内容…...
深度学习之处理多维特征的输入
我们首先来看一个糖尿病的数据集: 在数据集中,我们称每一行叫做sample,表示一个样本,称每一列是feature,也就是特征在数据库里面这就是一个关系表,每一行叫做记录,每一列叫做字段。 每一个样本都…...
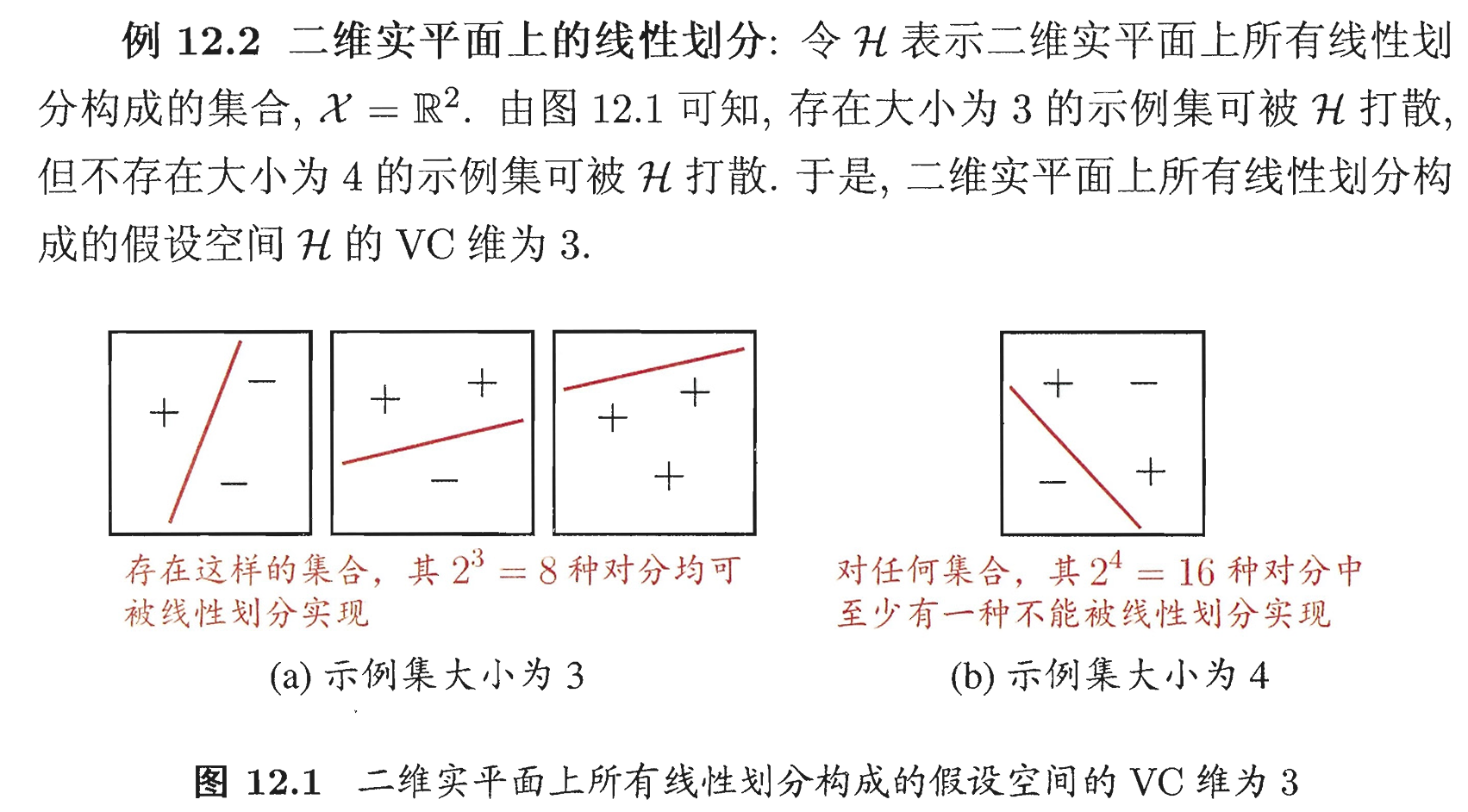
西瓜书读书笔记整理(十二) —— 第十二章 计算学习理论(下)
第十二章 计算学习理论(下) 12.4 VC 维(Vapnik-Chervonenkis dimension)12.4.1 什么是 VC 维12.4.2 增长函数(growth function)、对分(dichotomy)和打散(shattering&…...

初探分布式链路追踪
本篇文章,主要介绍应用如何正确使用日志系统,帮助用户从依赖、输出、清理、问题排查、报警等各方面全面掌握。 可观测性 可观察性不单是一套理论框架,而且并不强制具体的技术规格。其核心在于鼓励团队内化可观察性的理念,并确保由…...
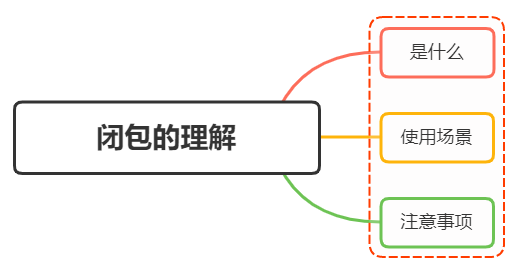
闭包的理解?闭包使用场景
说说你对闭包的理解?闭包使用场景 #一、是什么 一个函数和对其周围状态(lexical environment,词法环境)的引用捆绑在一起(或者说函数被引用包围),这样的组合就是闭包(closure&#…...

openssl3.2 - 帮助文档的整理
文章目录 openssl3.2 - 帮助文档的整理概述笔记整理后, 非空的文件夹如下整理后, 留下的有点用的文件列表如下备注END openssl3.2 - 帮助文档的整理 概述 openssl3.2源码工程编译安装完, 对于库的使用者, 有用的文档, 远不止安装的那些html. 用everything查找, 配合手工删除,…...
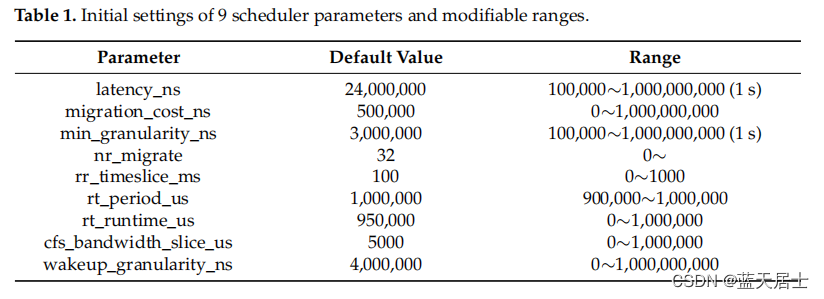
中移(苏州)软件技术有限公司面试问题与解答(5)—— Linux进程调度参数调优是如何通过代码实际完成的1
接前一篇文章:中移(苏州)软件技术有限公司面试问题与解答(0)—— 面试感悟与问题记录 本文对于中移(苏州)软件技术有限公司面试问题中的“(11)Linux进程调度参数调优是如…...

初识C语言·文件操作
目录 1 关于文件 i)文件的基本知识 ii)数据文件的分类 2 文件打开和关闭 i)流和标准流 ii)文件指针 iii)文件打开和关闭 3 文件的顺序读写 i) fgetc fputc ii) fgets fputs iii) fscanf fprintf iv) fwrite fread 4 对比一组函数 scanf/fscanf/sscanf/printf/fpri…...

跨境卖家:如何利用自养号测评抢占市场先机?
在当今的跨境电商领域,产品的销量和评价是影响产品在市场上的表现的关键因素。对于卖家而言,自行养号进行产品测评不仅有助于提升销量,更成为了他们在这个竞争激烈的市场中保持竞争力的必备策略。 相较于一些卖家仍然依赖于服务商进行测评&a…...

开发手札:Github Timeout 22
今天(2024.01.26日),提交github又出现了ssh connect timeout errorcode 22,不论是创建新的sshkey还是配置.ssh/config都没用。 偶然在知乎上看到了解决方案,只需要在host中添加: 140.82.113.4 githu…...
)
学习鸿蒙基础(3)
1.组件重用样式 如果每个组件的样式都需要单独设置,在开发过程中会出现大量代码在进行重复样式设置,虽然可以复制粘贴,但为了代码简洁性和后续方便维护,可以采用公共样式进行复用的装饰器Styles。 Styles装饰器可以将多条样式设置…...

2024/1/27 备战蓝桥杯 1-2
目录 金币 0金币 - 蓝桥云课 (lanqiao.cn) 天干地支 0天干地支 - 蓝桥云课 (lanqiao.cn) 明明的随机数 0明明的随机数 - 蓝桥云课 (lanqiao.cn) 浇灌 0灌溉 - 蓝桥云课 (lanqiao.cn) 金币 0金币 - 蓝桥云课 (lanqiao.cn) 思路:放两种情况(k:代…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...
