C++/数据结构:二叉搜索树的实现与应用
目录
一、二叉搜索树简介
二、二叉搜索树的结构与实现
2.1二叉树的查找与插入
2.2二叉树的删除
2.3二叉搜索树的实现
2.3.1非递归实现
2.3.2递归实现
三、二叉搜索树的k模型和kv模型
一、二叉搜索树简介

二、二叉搜索树的结构与实现
2.1二叉树的查找与插入
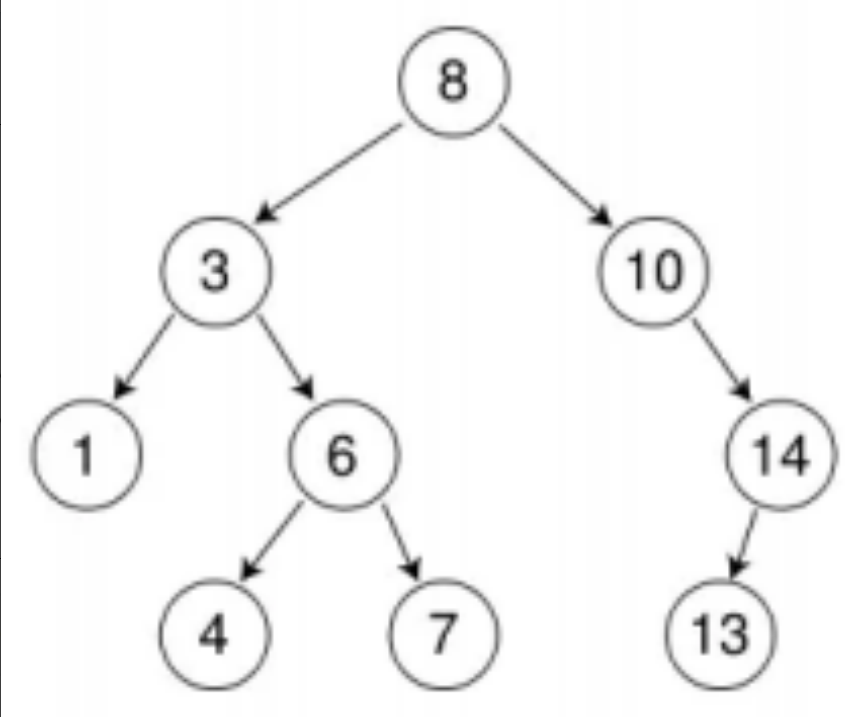
| int a [] = { 8 , 3 , 1 , 10 , 6 , 4 , 7 , 14 , 13 }; |
2.2二叉树的删除
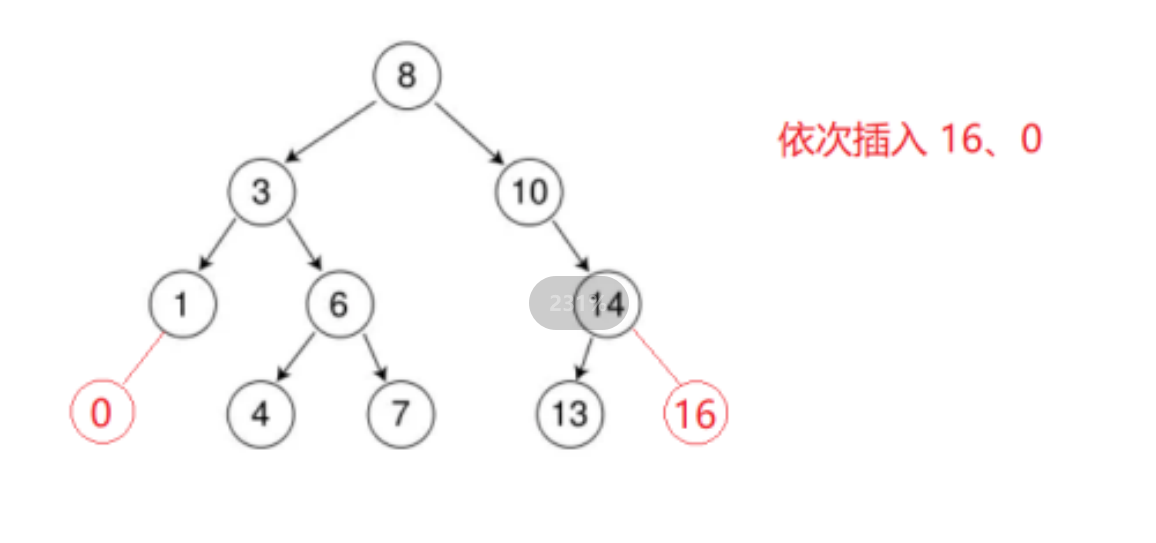
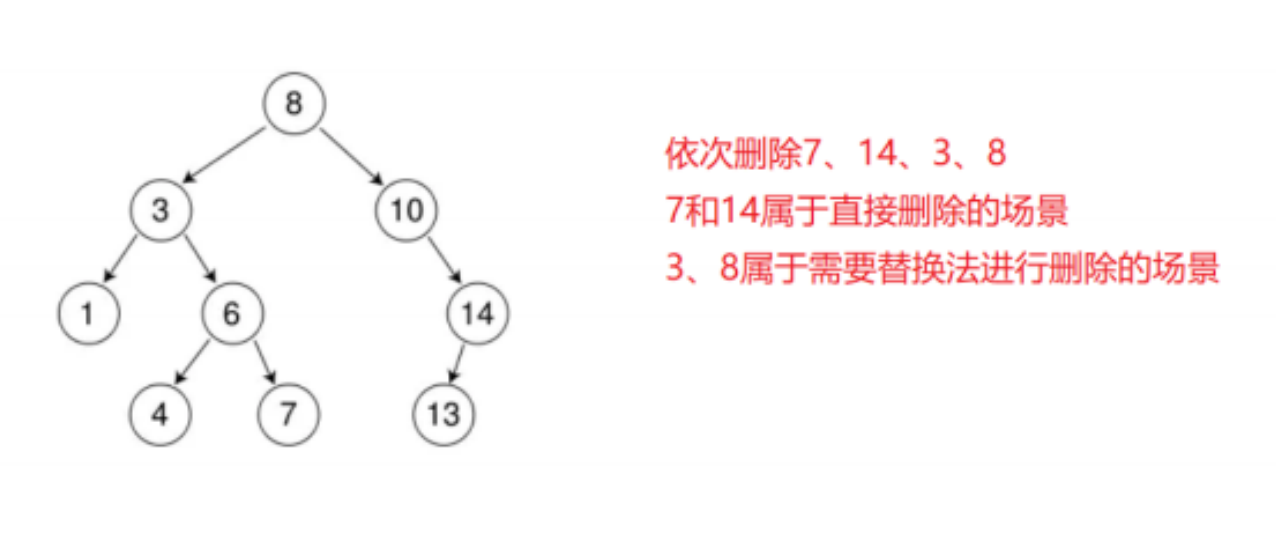
2.3二叉搜索树的实现
2.3.1非递归实现
//二叉树节点的构建
template<class K>struct BSTreeNode{typedef BSTreeNode<K> Node;Node* _left;Node* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}};//class BinarySearchTreetemplate<class K>class BSTree{typedef BSTreeNode<K> Node;public:// 强制生成默认构造BSTree() = default;//拷贝构造BSTree(const BSTree<K>& t){_root = Copy(t._root);}//赋值拷贝BSTree<K>& operator=(BSTree<K> t){swap(_root, t._root);return *this;}//析构函数~BSTree(){Destroy(_root);}/////增删查改//插入数据bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}//查找数据bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;}//删除数据bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (cur == parent->_right){parent->_right = cur->_right;}else{parent->_left = cur->_right;}}delete cur;return true;}else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{if (cur == parent->_right){parent->_right = cur->_left;}else{parent->_left = cur->_left;}}delete cur;return true;}else{// 替换法Node* rightMinParent = cur;Node* rightMin = cur->_right;while (rightMin->_left){rightMinParent = rightMin;rightMin = rightMin->_left;}cur->_key = rightMin->_key;if (rightMin == rightMinParent->_left)rightMinParent->_left = rightMin->_right;elserightMinParent->_right = rightMin->_right;delete rightMin;return true;}}}return false;}private:Node* _root;};2.3.2递归实现
//二叉树节点的构建
template<class K>struct BSTreeNode{typedef BSTreeNode<K> Node;Node* _left;Node* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}};//class BinarySearchTreetemplate<class K>class BSTree{typedef BSTreeNode<K> Node;public:// 强制生成默认构造BSTree() = default;//拷贝构造BSTree(const BSTree<K>& t){_root = Copy(t._root);}//赋值拷贝BSTree<K>& operator=(BSTree<K> t){swap(_root, t._root);return *this;}//析构函数~BSTree(){Destroy(_root);}/////增删查改bool FindR(const K& key){return _FindR(_root, key);}bool InsertR(const K& key){return _InsertR(_root, key);}bool EraseR(const K& key){return _EraseR(_root, key);}void InOrder(){_InOrder(_root);cout << endl;}private:void Destroy(Node* root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;}Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newRoot = new Node(root->_key);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;}//借助引用可以更好的删除和更改数据节点,不需要再额外创建父节点来更改bool _EraseR(Node*& root, const K& key){if (root == nullptr)return false;if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else{Node* del = root;if (root->_right == nullptr){root = root->_left;}else if (root->_left == nullptr){root = root->_right;}else{Node* rightMin = root->_right;while (rightMin->_left){rightMin = rightMin->_left;}swap(root->_key, rightMin->_key);return _EraseR(root->_right, key);}delete del;return true;}}bool _InsertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->_key < key){return _InsertR(root->_right, key);}else if (root->_key > key){return _InsertR(root->_left, key);}else{return false;}}bool _FindR(Node* root, const K& key){if (root == nullptr)return false;if (root->_key < key){return _FindR(root->_right, key);}else if (root->_key > key){return _FindR(root->_left, key);}else{return true;}}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}Node* _root;};三、二叉搜索树的k模型和kv模型
// 改造二叉搜索树为KV结构
template<class K, class V>
struct BSTNode{BSTNode(const K& key = K(), const V& value = V()): _pLeft(nullptr) , _pRight(nullptr), _key(key), _Value(value){}BSTNode<T>* _pLeft;BSTNode<T>* _pRight;K _key;V _value};
template<class K, class V>
class BSTree{typedef BSTNode<K, V> Node;typedef Node* PNode;
public:BSTree(): _pRoot(nullptr){}PNode Find(const K& key);bool Insert(const K& key, const V& value)bool Erase(const K& key)
private:PNode _pRoot;};void TestBSTree()
{// 输入单词,查找单词对应的中文翻译BSTree<string, string> dict;dict.Insert("string", "字符串");dict.Insert("tree", "树");dict.Insert("left", "左边、剩余");dict.Insert("right", "右边");dict.Insert("sort", "排序");// 插入词库中所有单词string str;while (cin>>str){BSTreeNode<string, string>* ret = dict.Find(str);if (ret == nullptr){cout << "单词拼写错误,词库中没有这个单词:" <<str <<endl;}else{cout << str << "中文翻译:" << ret->_value << endl;}}
}相关文章:

C++/数据结构:二叉搜索树的实现与应用
目录 一、二叉搜索树简介 二、二叉搜索树的结构与实现 2.1二叉树的查找与插入 2.2二叉树的删除 2.3二叉搜索树的实现 2.3.1非递归实现 2.3.2递归实现 三、二叉搜索树的k模型和kv模型 一、二叉搜索树简介 二叉搜索树又称二叉排序树,它或者是一棵空树࿰…...
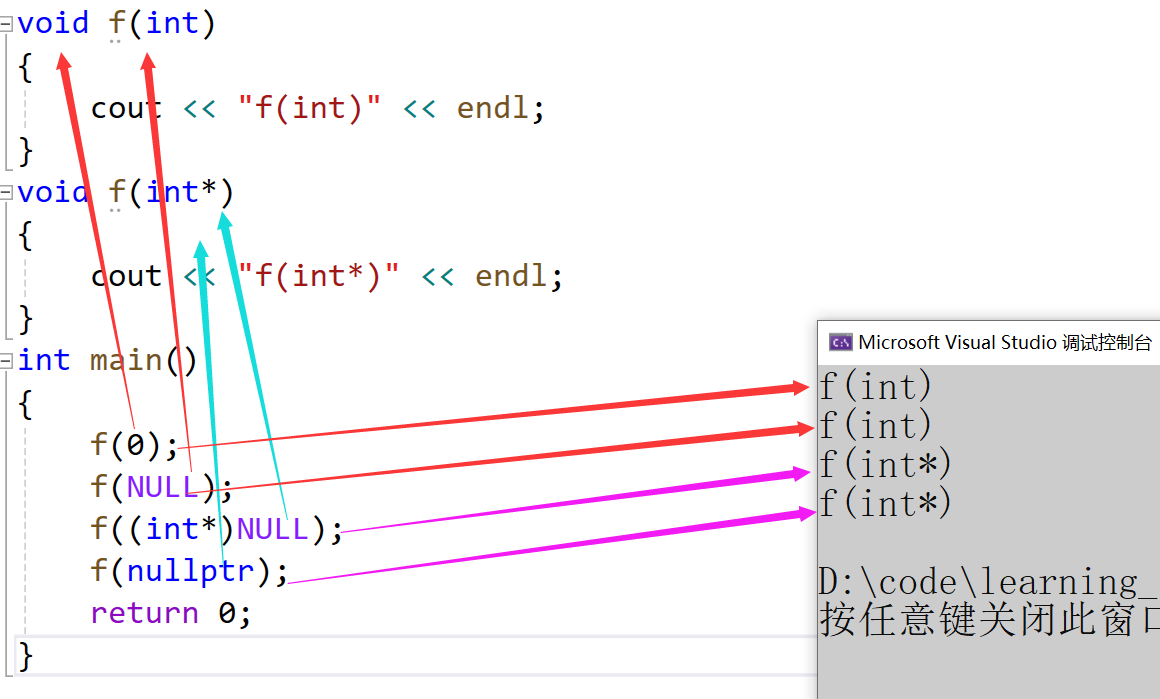
C++引用、内联函数、auto关键字介绍以及C++中无法使用NULL的原因
文章目录 一、引用1.1 引用概念1.2 引用特性1.3 常引用1.4 使用场景1.4.1 做参数1.4.2做返回值 1.5 引用和指针的区别1.6 小结一下 二、内联函数2.1 内联的概念2.2 内联的特性2.3 【面试题】 三、auto关键字(C11)3.1 类型别名思考3.2 auto简介 四、auto的使用细则4.1 基于范围的…...
RabbitMQ之三种队列之间的区别及如何选型
目录 不同队列之间的区别 Classic经典队列 Quorum仲裁队列 Stream流式队列 如何使用不同类型的队列 Quorum队列 Stream队列 不同队列之间的区别 Classic经典队列 这是RabbitMQ最为经典的队列类型。在单机环境中,拥有比较高的消息可靠性。 经典队列可以选…...

【ArcGIS微课1000例】0099:土地利用变化分析
本实验讲述在ArcGIS软件中基于两期土地利用数据,做土地利用变化分析。 文章目录 一、实验描述二、实验过程三、注意事项一、实验描述 对城市土地利用情况进行分析时,需要考虑不同时期土地利用图层在空间上的差异性,如农用地转建筑用地的空间变化。而该变化过程表现为各时期…...
学习鸿蒙基础(2)
arkts是声名式UI DevEcoStudio的右侧预览器可以预览。有个TT的图标可以看布局的大小。和html的布局浏览很像。 上图布局对应的代码: Entry //入口 Component struct Index {State message: string Hello Harmonyos //State 数据改变了也刷新的标签build() {Row()…...

2024年美国大学生数学建模竞赛思路与源代码【2024美赛C题】
B站账号,提前关注,会有直播:有为社的个人空间-有为社个人主页-哔哩哔哩视频 (bilibili.com) 题目 待定 问题一 思路 待定 模型 待定 程序 待定 问题二 待定 思路 待定 模型 待定 程序 待定...
Windows11搭建GPU版本PyTorch环境详细过程
Anaconda安装 https://www.anaconda.com/ Anaconda: 中文大蟒蛇,是一个开源的Python发行版本,其包含了conda、Python等180多个科学包及其依赖项。从官网下载Setup:点击安装,之后勾选上可以方便在普通命令行cmd和PowerShell中使用…...

Springboot项目基础配置:小白也能快速上手!
推荐文章 给软件行业带来了春天——揭秘Spring究竟是何方神圣(一) 给软件行业带来了春天——揭秘Spring究竟是何方神圣(二) 给软件行业带来了春天——揭秘Spring究竟是何方神圣(三) 给软件行业带来了春天—…...
20240127在ubuntu20.04.6下配置whisper
20240131在ubuntu20.04.6下配置whisper 2024/1/31 15:48 首先你要有一张NVIDIA的显卡,比如我用的PDD拼多多的二手GTX1080显卡。【并且极其可能是矿卡!】800¥ 2、请正确安装好NVIDIA最新的驱动程序和CUDA。可选安装! 3、配置whispe…...

C# 递归执行顺序
为了方便进一步理解递归,写了一个数字输出 class Program {static void Main(string[] args){int number 5;RecursiveDecrease(number);}static void RecursiveDecrease(int n){if (n > 0){Console.WriteLine("Before recursive call do : " n);Rec…...
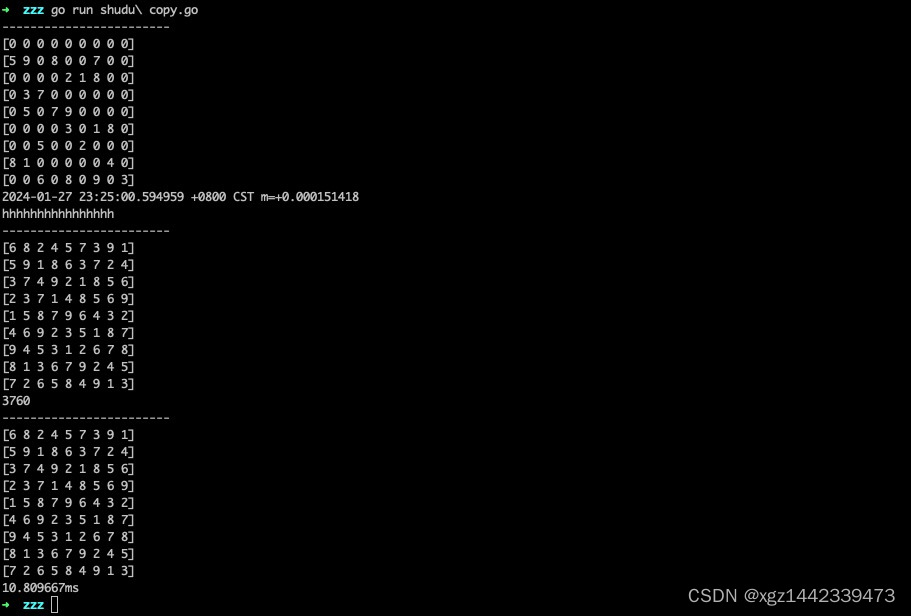
go 实现暴力破解数独
一切罪恶的来源是昨晚睡前玩了一把数独,找虐的选了个最难的模式,做了一个多小时才做完,然后就睡不着了..........程序员不能受这委屈,今天咋样也得把这玩意儿破解了 破解思路(暴力破解加深度遍历) 把数独…...

go语言-字符串处理常用函数
本文介绍go语言处理字符串类型的常见函数。 ## 多行字符串 在 Go 中创建多行字符串非常容易。只需要在你声明或赋值时使用 () 。 str : This is a multiline string. ## 字符串的拼接 go // fmt.Sprintf方式拼接字符串 str1 : "abc" str2 : "def" …...
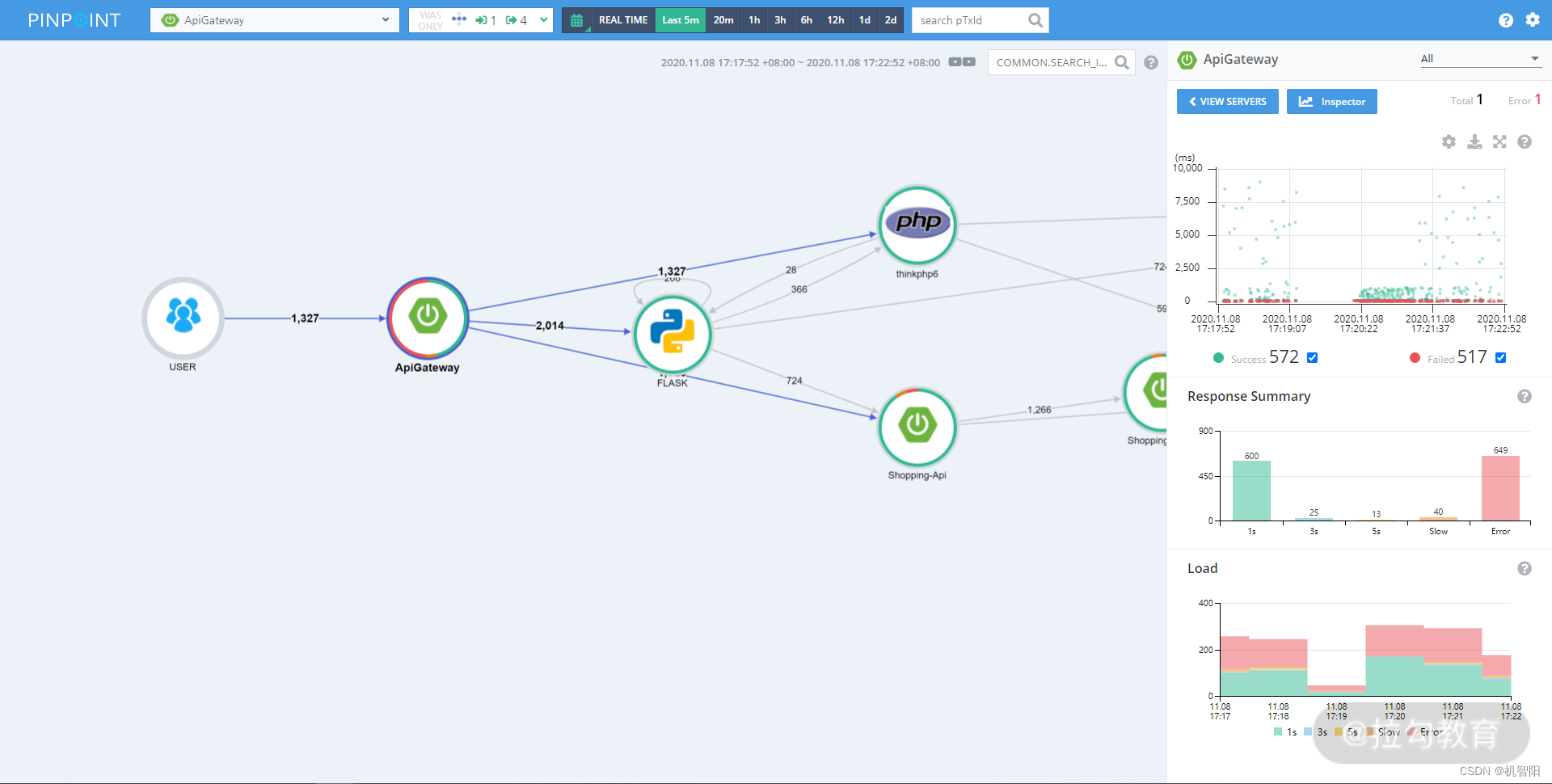
DevOps落地笔记-05|非功能需求:如何有效关注非功能需求
上一讲主要介绍了看板方法以及如何使用看板方法来解决软件研发过程中出现的团队过载、工作不均、任务延期等问题。通过学习前面几个课时介绍的知识,你的团队开始源源不断地交付用户价值。用户对交付的功能非常满意,但等到系统上线后经常出现服务不可用的…...
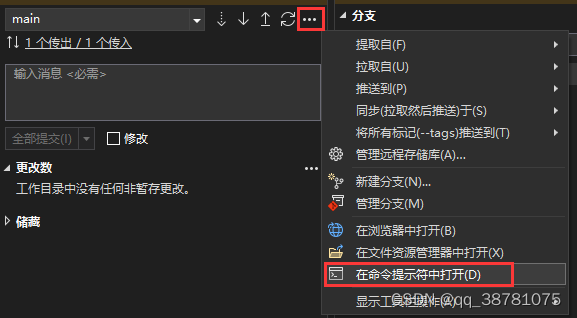
vs 撤销本地 commit 并保留更改
没想到特别好的办法,我想的是用 vs 打开 git 命令行工具 然后通过 git 命令来撤销提交,尝试之前建议先建个分支实验,以免丢失代码, git 操作见 git 合并多个 commit / 修改上一次 commit...

深度解读NVMe计算存储协议-1
随着云计算、企业级应用以及物联网领域的飞速发展,当前的数据处理需求正以前所未有的规模增长,以满足存储行业不断变化的需求。这种增长导致网络带宽压力增大,并对主机计算资源(如内存和CPU)造成极大负担,进…...
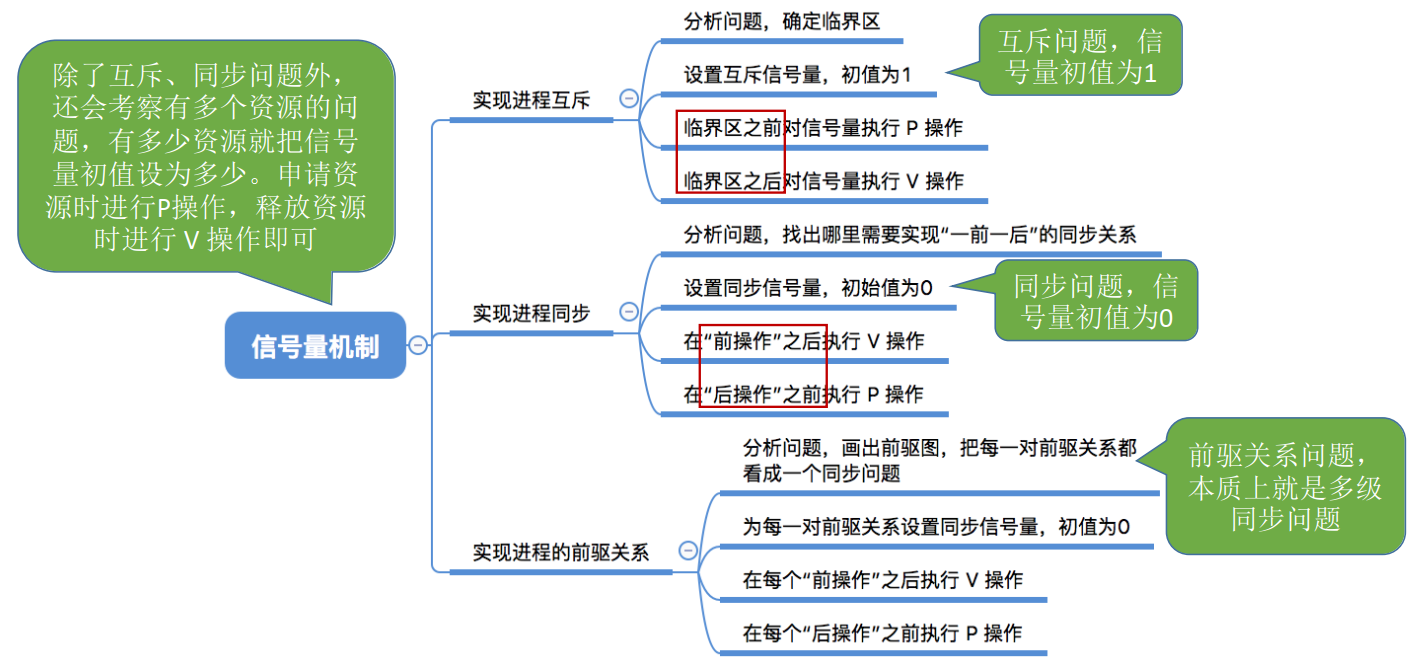
CHS_06.2.3.4_2+用信号量实现进程互斥、同步、前驱关系
CHS_06.2.3.4_2用信号量实现进程互斥、同步、前驱关系 知识总览信号量机制实现进程互斥信号量机制实现进程同步信号量机制实现前驱关系 知识回顾 各位同学 大家好 在这个小节中 我们要学习怎么用信号量机制来实现进程的同步互制关系 知识总览 那么 我们之前学习了互斥的几种软…...
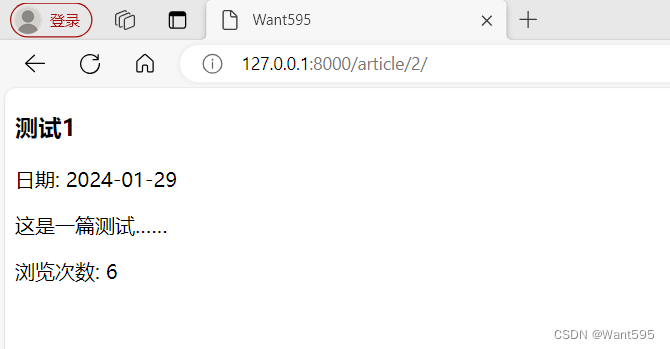
Web实战丨基于Django的简单网页计数器
文章目录 写在前面Django简介主要程序运行结果系列文章写在后面 写在前面 本期内容 基于django的简单网页计数器 所需环境 pythonpycharm或vscodedjango 下载地址 https://download.csdn.net/download/m0_68111267/88795604 Django简介 Django 是一个用 Python 编写的高…...

mysql8安装基础操作(一)
一、下载mysql8.0 1.查看系统glibc版本 这里可以看到glibc版本为2.17,所以下载mysql8.0的版本时候尽量和glibc版本对应 [rootnode2 ~]# rpm -qa |grep -w glibc glibc-2.17-222.el7.x86_64 glibc-devel-2.17-222.el7.x86_64 glibc-common-2.17-222.el7.x86_64 gl…...
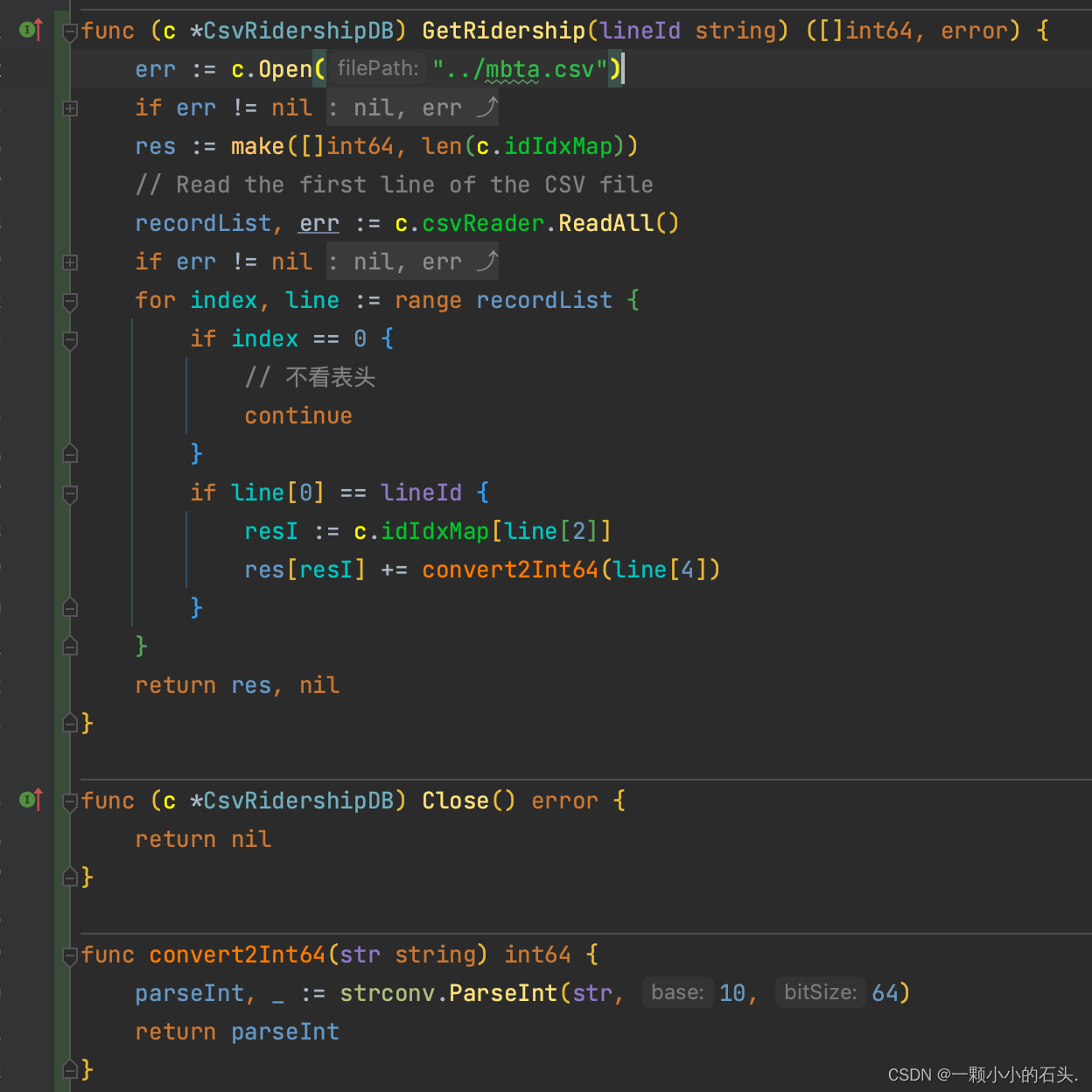
MIT6.5830 实验0
前置 本次实验使用 Golang 语言实现,在之前的年份中,都是像 cs186 那样使用 Java 实现。原因: Golang 语言作为现代化语言,简单易上手但功能强大。 使参加实验的同学有同一起跑线,而不是像Java那样,有些同…...
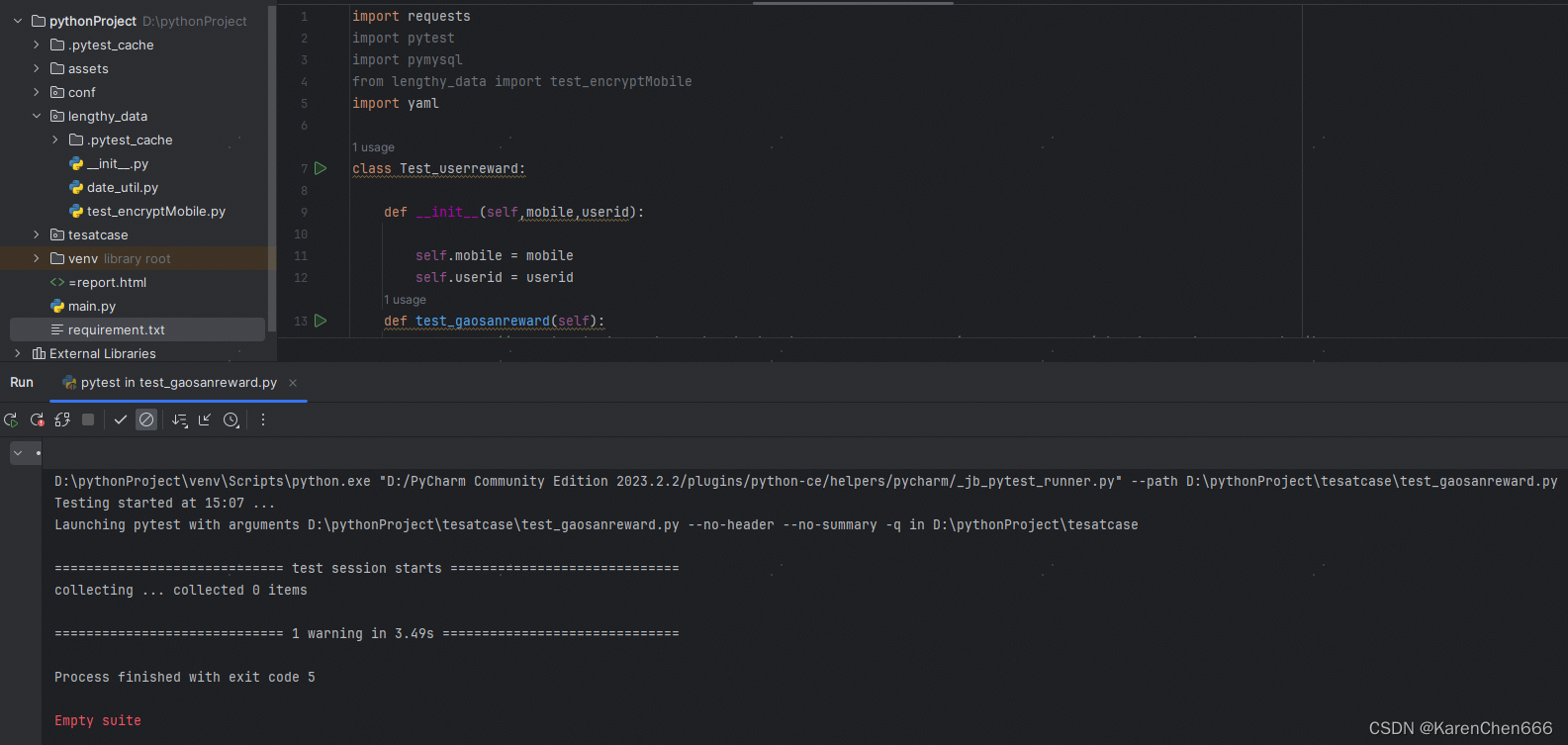
【简便方法和积累】pytest 单元测试框架中便捷安装插件和执行问题
又来进步一点点~~~ 背景:之前写了两篇关于pytest单元测试框架的文章,本篇内容对之前的做一个补充 一、pytest插件: pytest 有非常多的插件,很方便,以下为插件举例: pytest,pytest-html&#x…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...
