Unity点乘和叉乘
目录
前言
点乘
一、点乘是什么?
二、应用
三、使用步骤
1.代码示例
叉乘
一、叉乘是什么?
二、应用
三、使用步骤
1.代码示例
总结
前言
Unity中经常会用到向量的运算来计算目标的方位,朝向,角度等相关数据,而这些计算中最常用的就是点乘和叉乘
点乘
一、点乘是什么?
- 定义:a·b=|a|·|b|cos<a,b> 【注:小写字母表示向量,<a,b>表示向量a,b的夹角,取值范围为[0,180]】
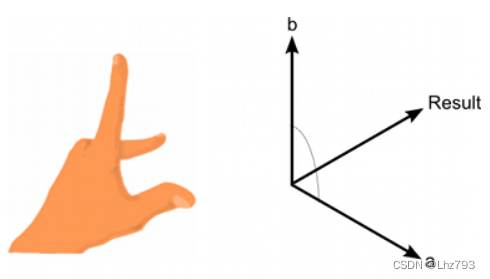
- 几何意义:一条边向另一条边的投影乘以另一条边的长度(如图所示)

- 性质1: a*b = |a||b|Cos(θ) ,θ是向量a 和向量 b之间的夹角。
- 性质2: a*b = b*a 满足乘法交换律
- 注意 : 结果不是一个向量,而是一个标量。
二、应用
- 根据点乘计算两个向量的夹角。<a,b>= arccos(a·b / (|a|·|b|))
- 根据点乘的正负值,得到夹角大小范围,点乘>0,则夹角(0,90),点乘<0,则夹角(90,180),可以利用这点判断一个多边形是面向摄像机还是背向摄像机。
- 根据点乘的大小,得到向量的投影长度,反应了向量的长度关系。
- 在生产生活中,点积应用广泛。利用点积可判断一个多边形是否面向摄像机还是背向摄像机。向量的点积与它们夹角的余弦成正比,因此在聚光灯的效果计算中,可以根据点积来得到光照效果,如果点积越大,说明夹角越小,则物理离光照的轴线越近,光照越强。物理中,点积可以用来计算合力和功。若b为单位矢量,则点积即为a在方向b的投影,即给出了力在这个方向上的分解。功即是力和位移的点积。计算机图形学常用来进行方向性判断,如两矢量点积大于0,则它们的方向朝向相近;如果小于0,则方向相反。矢量内积是人工智能领域中的神经网络技术的数学基础之一,此方法还被用于动画渲染(Animation-Rendering)。
三、使用步骤
1.代码示例
代码如下(示例):
/// <summary>/// 点积/// </summary>/// <param name="a"></param>/// <param name="b"></param>private void TestDot(Vector3 a, Vector3 b){// 计算 a、b 点积结果float result = Vector3.Dot(a, b);// 通过向量直接获取两个向量的夹角(默认为 角度), 此方法范围 [0 - 180]float angle = Vector3.Angle(a, b);// 计算 a、b 单位向量的点积,得到夹角余弦值,|a.normalized|*|b.normalized|=1;result = Vector3.Dot(a.normalized, b.normalized);// 通过反余弦函数获取 向量 a、b 夹角(默认为 弧度)float radians = Mathf.Acos(result);// 将弧度转换为 角度angle = radians * Mathf.Rad2Deg;}
叉乘
一、叉乘是什么?
- 定义:
c = a x b,其中a b c均为向量得到一个与这两个向量都垂直的向量,这个向量的模是以两个向量为边的平行四边形的面积
- 几何意义:
v1和v2向量的叉乘运算:相应元素的乘积的和:v1( x1, y1,z1) x v2(x2, y2, z2) = (y1*z2 - y2*z1)i+(x2*z1 - x1*z2)j+(x1*y2-x2*y1)k;
-
利用三阶行列式计算:
|i j k|
|x1 y1 z1|
|x2 y2 z2|

- 性质1: c⊥a,c⊥b,即向量c与向量a,b所在平面垂直
- 性质2:模长|c| = |a||b| sin<a,b>
- 性质3:(数学上)满足右手法则, a x b = -b x a,所以我们可以使用叉乘的正负值来判断a,b的相对位置,即b是处于a的顺时针还是逆时针方向。
- 注意 :
叉乘的右手定则是用来确定叉乘积的方向的。
右手法则:右手的四指方向指向第一个矢量,屈向叉乘矢量的夹角方向(两个矢量夹角方向取小于180°的方向),那么此时大拇指方向就是叉乘所得的叉乘矢量的方向.(大拇指应与食指成九十度)(注意:Unity当中使用左手,因为Unity使用的是左手坐标系)
二、应用
- 1.根据叉乘得到a,b向量的相对位置,和顺时针或逆时针方位。
- 简单的说: 点乘判断角度,叉乘判断方向。形象的说: 当一个敌人在你身后的时候,叉乘可以判断你是往左转还是往右转更好的转向敌人,点乘得到你当前的面朝向的方向和你到敌人的方向的所成的角度大小。
- 2.得到a,b夹角的正弦值,计算向量的夹角(0,90),可以配合点乘和Angle方法计算出含正负的方向。
- 3.根据叉乘大小,得到a,b向量所形成的平行四边形的面积大小,根据面积大小得到向量的相对大小。
三、使用步骤
1.代码示例
代码如下(示例):
/// <summary>/// 叉乘/// </summary>/// <param name="a"></param>/// <param name="b"></param>private void TestCross(Vector3 a, Vector3 b){//计算向量 a、b 的叉积,结果为 向量 Vector3 c = Vector3.Cross(a, b);// 通过反正弦函数获取向量 a、b 夹角(默认为弧度)float radians = Mathf.Asin(Vector3.Distance(Vector3.zero, Vector3.Cross(a.normalized, b.normalized)));float angle = radians * Mathf.Rad2Deg;// 判断顺时针、逆时针方向,是在 2D 平面内的,所以需指定一个平面,//下面以X、Z轴组成的平面为例 , (Y 轴为纵轴),// 在 X、Z 轴平面上,判断 b 在 a 的顺时针或者逆时针方向,if (c.y > 0){// b 在 a 的顺时针方向}else if (c.y == 0){// b 和 a 方向相同(平行)}else{// b 在 a 的逆时针方向}} // 获取两个向量的夹角 Vector3.Angle 只能返回 [0, 180] 的值// 如真实情况下向量 a 到 b 的夹角(80 度)则 b 到 a 的夹角是(-80)// 通过 Dot、Cross 结合获取到 a 到 b, b 到 a 的不同夹角private void GetAngle(Vector3 a, Vector3 b){Vector3 c = Vector3.Cross(a, b);float angle = Vector3.Angle(a, b);// b 到 a 的夹角float sign = Mathf.Sign(Vector3.Dot(c.normalized, Vector3.Cross(a.normalized, b.normalized)));float signed_angle = angle * sign;Debug.Log("b -> a :" + signed_angle);// a 到 b 的夹角sign = Mathf.Sign(Vector3.Dot(c.normalized, Vector3.Cross(b.normalized, a.normalized)));signed_angle = angle * sign;Debug.Log("a -> b :" + signed_angle);}总结
点乘可以判断出目标物体在我的前方还是后方。大于零在前方,小于零在后方。
叉乘可以判断出目标物体在我的左边还是右边。大于零在右方,小于零在左方。
相关文章:

Unity点乘和叉乘
目录 前言 点乘 一、点乘是什么? 二、应用 三、使用步骤 1.代码示例 叉乘 一、叉乘是什么? 二、应用 三、使用步骤 1.代码示例 总结 前言 Unity中经常会用到向量的运算来计算目标的方位,朝向,角度等相关数据࿰…...

【ACL 2023】Enhancing Document-level EAE with Contextual Clues and Role Relevance
【ACL 2023】Enhancing Document-level Event Argument Extraction with Contextual Clues and Role Relevance 论文:https://aclanthology.org/2023.findings-acl.817/ 代码:https://github.com/LWL-cpu/SCPRG-master Abstract 与句子级推理相比&…...
Vue ECharts X轴 type为value的数据格式 + X轴固定间隔并向上取整十位数 - 附完整示例
ECharts:一个基于 JavaScript 的开源可视化图表库。 目录 效果 一、介绍 1、官方文档:Apache ECharts 2、官方示例 二、准备工作 1、安装依赖包 2、示例版本 三、使用步骤 1、在单页面引入 echarts 2、指定容器并设置容器宽高 3、数据处理&am…...
)
统计成绩(c++题解)
题目描述 半期考试结束了,几多欢喜几多愁!作为竞赛的选手,迟早是要经历大风大浪的,这点小小的涟漪无须太在意。但是对于成绩,还是要好好的分析一下的。 有N个学生,每个学生的数据包括学号、姓名、3门课的…...

【Qt】—— Hello World程序的实现
目录 (一)使⽤"按钮"实现 1.1 纯代码方式实现 1.2 可视化操作实现 (二)使⽤"标签"实现 2.1 纯代码方式实现 2.2 可视化操作实现 (一)使⽤"按钮"实现 1.1 纯代码方式实…...

谷歌浏览器网站打不开,显示叹号
问题: 您与此网站之间建立的连接不安全请勿在此网站上输入任何敏感信息(例如密码或信用卡信息),因为攻击者可能会盗取这些信息。 了解详情 解决方式: 网上有很多原因,亲测为DNS问题,设置&…...

怎么去除图片中不需要的部分?这三种高效方法快来试一下
在数字图像处理的浩瀚世界中,去除图片中不必要部分的任务,宛如一幅细致的画卷,需精心描绘。这些不必要部分,可能是背景、水印、无关紧要物体或错误部分,它们如同图片中的瑕疵,需要被巧妙地修饰或去除。这不…...

yolov5导出onnx模型问题
为了适配C工程代码,我在导出onnx模型时,会把models/yolo.py里面的forward函数改成下面这样, #转模型def forward(self, x):z [] # inference outputfor i in range(self.nl):x[i] self.m[i](x[i]) # convbs, _, ny, nx x[i].shape # x(…...
JS第一课简单看看这是啥东西
1.什么是JavaScript JS是一门编程语言,是一种运行在客户端(浏览器)的编程语言,主要是让前端的画面动起来,注意HTML和CSS不是编程语言,他俩是一种标记语言。JS只要有浏览器就能运行不用跟Python或者Java一样上来装一个jdk或者Pyth…...

2023年常用网络安全政策标准整合
文章目录 前言一、政策篇(一)等级保护(二)关键信息基础设施保护(三)数据安全(四)数据出境安全评估(五)网络信息安全(六)应急响应(七)网络安全专用产品检测认证制度(八)个人信息保护(九)商用密码二、标准篇前言 2023年,国家网络安全政策和标准密集发布,逐渐…...
Redis -- 背景知识
“知识就是力量” -- 弗朗西斯培根 目录 特性 为啥Redis快? 应用场景 Redis不能做什么? Redis是在内存中存储数据的一个中间件,用作为数据库,也可以用作为缓存,在分布式中有很高的威望。 特性 In-memory data structures&…...
如何在Shopee平台上进行手机类目选品?
在Shopee平台上进行手机类目的选品是一个关键而复杂的任务。卖家需要经过一系列的策略和步骤,以确保选品的成功和销售业绩的提升。下面将介绍一些有效的策略,帮助卖家在Shopee平台上进行手机类目选品。 先给大家推荐一款shopee知虾数据运营工具知虾免费…...

班级管理神器,教师在线发布系统
现如今,班级管理也需要与时俱进。传统的管理方式不仅效率低下,而且容易出错。为了更好地管理班级,教师需要一个强大的工具来帮助他们发布信息和管理学生。 发布系统是一款专门为教师设计的数字化管理工具。通过系统,老师们就可以…...

【Spring Boot 3】异步线程任务
【Spring Boot 3】异步线程任务 背景介绍开发环境开发步骤及源码工程目录结构总结背景 软件开发是一门实践性科学,对大多数人来说,学习一种新技术不是一开始就去深究其原理,而是先从做出一个可工作的DEMO入手。但在我个人学习和工作经历中,每次学习新技术总是要花费或多或…...

JAVA斗地主逻辑-控制台版
未排序版: 准备牌->洗牌 -> 发牌 -> 看牌: App程序入口: package doudihzu01;public class App {public static void main(String[] args) {/*作为斗地主程序入口这里不写代码逻辑*///无参创建对象,作为程序启动new PokerGame();…...
Harmony的自定义组件和Page的数据同步
在开发过程中会经常使用自定义组件,就会遇到一个问题,在页面中引入组件后,如何把改变的值传递到自定义组件中呢,这就用到了装饰器,在这是单向传递的,用的装饰器是@State和@Prop @State在page页面中监听数据的变化 @Prop在自定义组件中监听page页面传递过来的变化值,并赋…...

【Vue3+Vite】路由机制router 快速学习 第四期
文章目录 路由简介路由是什么路由的作用 一、路由入门案例1. 创建项目 导入路由依赖2. 准备页面和组件3. 准备路由配置4. main.js引入router配置 二、路由重定向三、编程式路由(useRouter)四、路由传参(useRoute)五、路由守卫总结 路由简介 路由是什么 路由就是根据不同的 URL…...

python脚本实现浏览器驱动chromedriver的版本自动升级
chromedriver的版本号与chrome浏览器版本不匹配时在运行程序时就会报错 用下面的脚本可以自动安装chromedriver的最新版本到指定路径 from webdriver_manager.utils import get_browser_version_from_os from webdriver_manager.chrome import ChromeDriverManager import re…...

npm使用国内淘宝镜像
一、命令配置 1、设置淘宝镜像源 npm config set registry https://registry.npmmirror.com2、查看镜像使用状态 npm config get registry如果返回https://registry.npmmirror.com/,说明配置的是淘宝镜像。 如果返回https://registry.npmjs.org/,说明配置的是官网镜像。 二…...
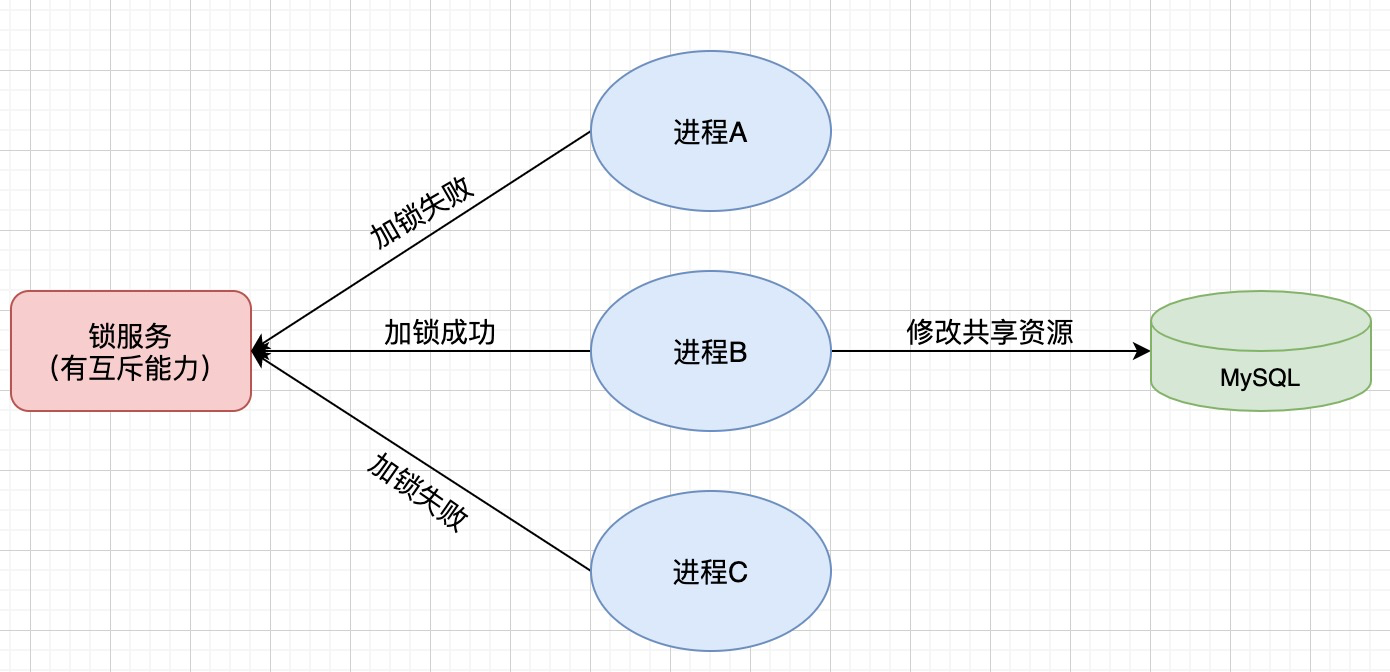
# Redis 分布式锁如何自动续期
Redis 分布式锁如何自动续期 何为分布式 分布式,从狭义上理解,也与集群差不多,但是它的组织比较松散,不像集群,有一定组织性,一台服务器宕了,其他的服务器可以顶上来。分布式的每一个节点&…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
