代码随想录算法训练营第二十四天|● 理论基础 ● 77. 组合
仅做学习笔记,详细请访问代码随想录
● 理论基础
● 77. 组合
● 理论基础
回溯法解决的问题
回溯法,一般可以解决如下几种问题:
组合问题:N个数里面按一定规则找出k个数的集合
切割问题:一个字符串按一定规则有几种切割方式
子集问题:一个N个数的集合里有多少符合条件的子集
排列问题:N个数按一定规则全排列,有几种排列方式
棋盘问题:N皇后,解数独等等
回溯法模板
这里给出Carl总结的回溯算法模板。
在讲二叉树的递归 (opens new window)中我们说了递归三部曲,这里我再给大家列出回溯三部曲。
回溯函数模板返回值以及参数
在回溯算法中,我的习惯是函数起名字为backtracking,这个起名大家随意。
回溯算法中函数返回值一般为void。
再来看一下参数,因为回溯算法需要的参数可不像二叉树递归的时候那么容易一次性确定下来,所以一般是先写逻辑,然后需要什么参数,就填什么参数。
但后面的回溯题目的讲解中,为了方便大家理解,我在一开始就帮大家把参数确定下来。
回溯函数伪代码如下:
void backtracking(参数)
回溯函数终止条件
既然是树形结构,那么我们在讲解二叉树的递归 (opens new window)的时候,就知道遍历树形结构一定要有终止条件。
所以回溯也有要终止条件。
什么时候达到了终止条件,树中就可以看出,一般来说搜到叶子节点了,也就找到了满足条件的一条答案,把这个答案存放起来,并结束本层递归。
所以回溯函数终止条件伪代码如下:
if (终止条件) {
存放结果;
return;
}
回溯搜索的遍历过程
在上面我们提到了,回溯法一般是在集合中递归搜索,集合的大小构成了树的宽度,递归的深度构成的树的深度。
如图:
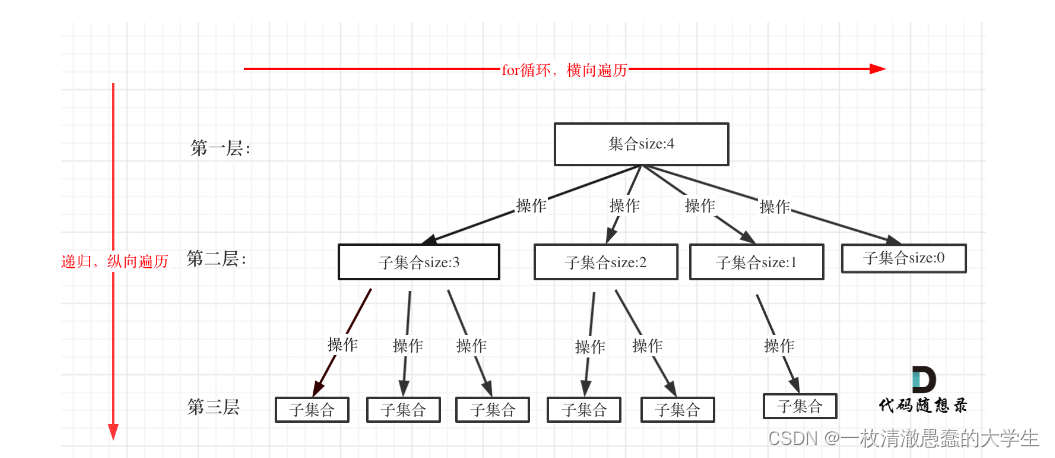
注意图中,我特意举例集合大小和孩子的数量是相等的!
回溯函数遍历过程伪代码如下:
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
for循环就是遍历集合区间,可以理解一个节点有多少个孩子,这个for循环就执行多少次。
大家可以从图中看出for循环可以理解是横向遍历,backtracking(递归)就是纵向遍历,这样就把这棵树全遍历完了,一般来说,搜索叶子节点就是找的其中一个结果了。
分析完过程,回溯算法模板框架如下:
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果
}
}
● 77. 组合
class Solution {
private:vector<vector<int>> result; // 存放符合条件结果的集合vector<int> path; // 用来存放符合条件结果void backtracking(int n, int k, int startIndex) {if (path.size() == k) {result.push_back(path);return;}for (int i = startIndex; i <= n; i++) {path.push_back(i); // 处理节点backtracking(n, k, i + 1); // 递归path.pop_back(); // 回溯,撤销处理的节点}}
public:vector<vector<int>> combine(int n, int k) {result.clear(); // 可以不写path.clear(); // 可以不写backtracking(n, k, 1);return result;}
};
相关文章:

代码随想录算法训练营第二十四天|● 理论基础 ● 77. 组合
仅做学习笔记,详细请访问代码随想录 ● 理论基础 ● 77. 组合 ● 理论基础 回溯法解决的问题 回溯法,一般可以解决如下几种问题: 组合问题:N个数里面按一定规则找出k个数的集合 切割问题:一个字符串按一定规则有几…...

买保险如何填健康告知
在投保健康险时,保险公司都有健康告知这一环,那么健康告知怎么机智的填? 人都吃五谷杂粮,身体免不了有各种小毛病,比如甲状腺结节等,健康告知通过不了怎么办? 健康告知是保险公司设计的健康问…...

云贝教育 | 【技术文章】Oracle 19c RAC修改网络
注: 本文为云贝教育 刘峰 原创,请尊重知识产权,转发请注明出处,不接受任何抄袭、和未经注明出处的转载。 原文链接:【Oracle 19c】Oracle 19c RAC修改网络 - 课程体系 - 云贝教育 (yunbee.net) 变更目标 ip类型 节点 原IP 目…...

Android SELinux:保护您的移动设备安全的关键
Android SELinux:保护您的移动设备安全的关键 1 引言 移动设备在我们的生活中扮演着越来越重要的角色,我们几乎把所有重要的信息都存储在这些设备上。然而,随着移动应用程序的数量不断增加,安全性也变得越来越关键。这就是为什么…...
)
第十三章认识Ajax(四)
认识FormData对象 FormData对象用于创建一个表示HTML表单数据的键值对集合。 它可以用于发送AJAX请求或通过XMLHttpRequest发送表单数据。 以下是FormData对象的一些作用: 收集表单数据:通过将FormData对象与表单元素关联,可以方便地收集表单中的数据。使用FormData对象,…...

使用 Node.js 和 Cheerio 爬取网站图片
写一个关于图片爬取的小案例 爬取效果 使用插件如下: {"dependencies": {"axios": "^1.6.0","cheerio": "^1.0.0-rc.12","request": "^2.88.2"} }新建一个config.js配置文件 // 爬取图片…...

2024美赛数学建模E题思路源码
赛题目的 可以将其拆解为以下主要问题,并为每个问题提出解决方案: 如何在极端天气事件越来越多的地区部署财产保险? 保险公司应在何时何地承保保单? 业主如何影响保险公司的承保决定? 如何建立能够评估未来房地产决…...

解决Docker AList本地挂载失效的问题。
解决Docker AList本地挂载失效的问题。 AList Docker version: 3.3 services:alist:image: xhofe/alist:latestcontainer_name: alistvolumes:- ./etc/alist:/opt/alist/data# 比如我要挂载/home,如果在docker里先挂载,是没法办法映射到linux系统下的/home的- /ho…...

Emmet常用语法总结
Emmet常用语法总结 子元素:>兄弟元素:上级元素:^倍数:*分组:()属性:[]id和类:# .迭代数字:$文本内容:{}注意事项 Emmet是许多流行文本编辑器的…...
获取系统当前最上层的Activity信息)
Android 12系统源码_页面管理(四)获取系统当前最上层的Activity信息
前言 很多应用开发人员,在日常开发过程中,经常会遇到一些需求,例如需要知道当前最上层的Activity是哪个,并结合这个Activity的名称来完成一些特定场景的需求。最简单的方法,是在创建Activity的时候将该Actvity存储到一…...

RK3588开发板Ubuntu与开发板使用U盘互传
1 将 U 盘(U 盘的格式必须为 FAT32 格式,大小在 32G 以下)插到开发板的 usb 接口,串口打印信息如下所示,U 盘的设备节点是/dev/sdb4。U 盘的设备节点不是固定的,根据实际情况来查看设备节点。 2 输入以下命令挂载 U 盘,…...
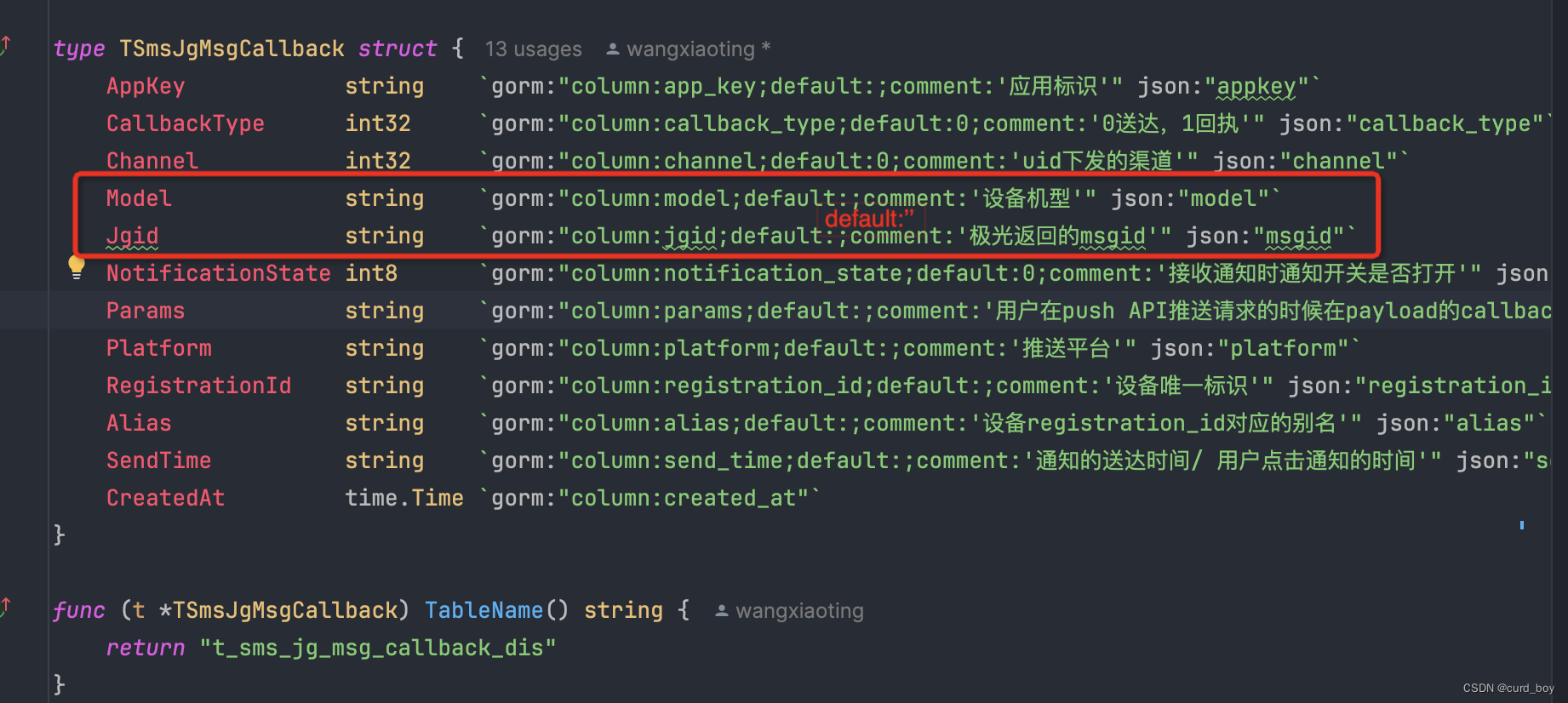
【BUG】golang gorm导入数据库报错 “unexpected type clause.Expr“
帮同事排查一个gorm导入数据报错的问题 事发现场 ck sql CREATE TABLE ods_api.t_sms_jg_msg_callback_dis (app_key String DEFAULT COMMENT 应用标识,callback_type Int32 DEFAULT 0 COMMENT 0送达,1回执,channel Int32 DEFAULT 0 COMMENT uid下发的渠道,mode…...
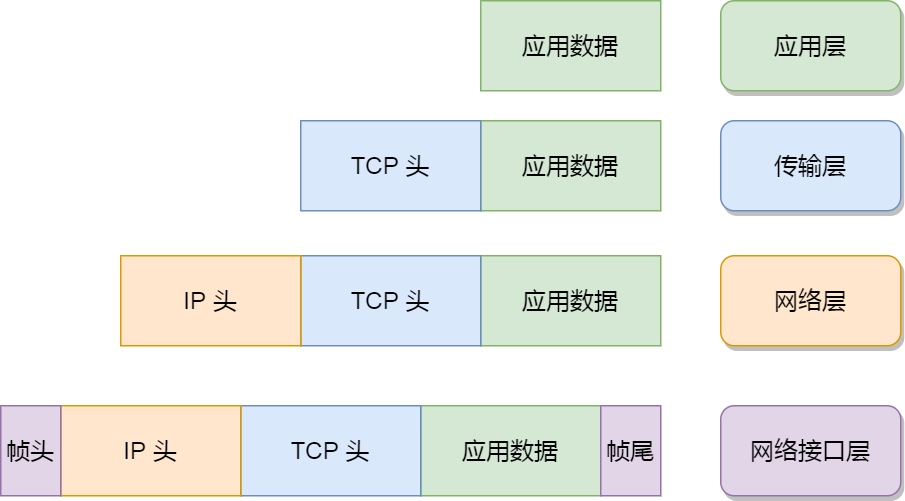
TCP/IP网络模型
大家好我是苏麟 , 今天聊聊TCP/IP四层网络模型 . 资料来源 : 小林coding 小林官方网站 : 小林coding (xiaolincoding.com) 应用层 最上层的,也是我们能直接接触到的就是应用层(Application Layer),我们电脑或手机使用的应用软件都…...
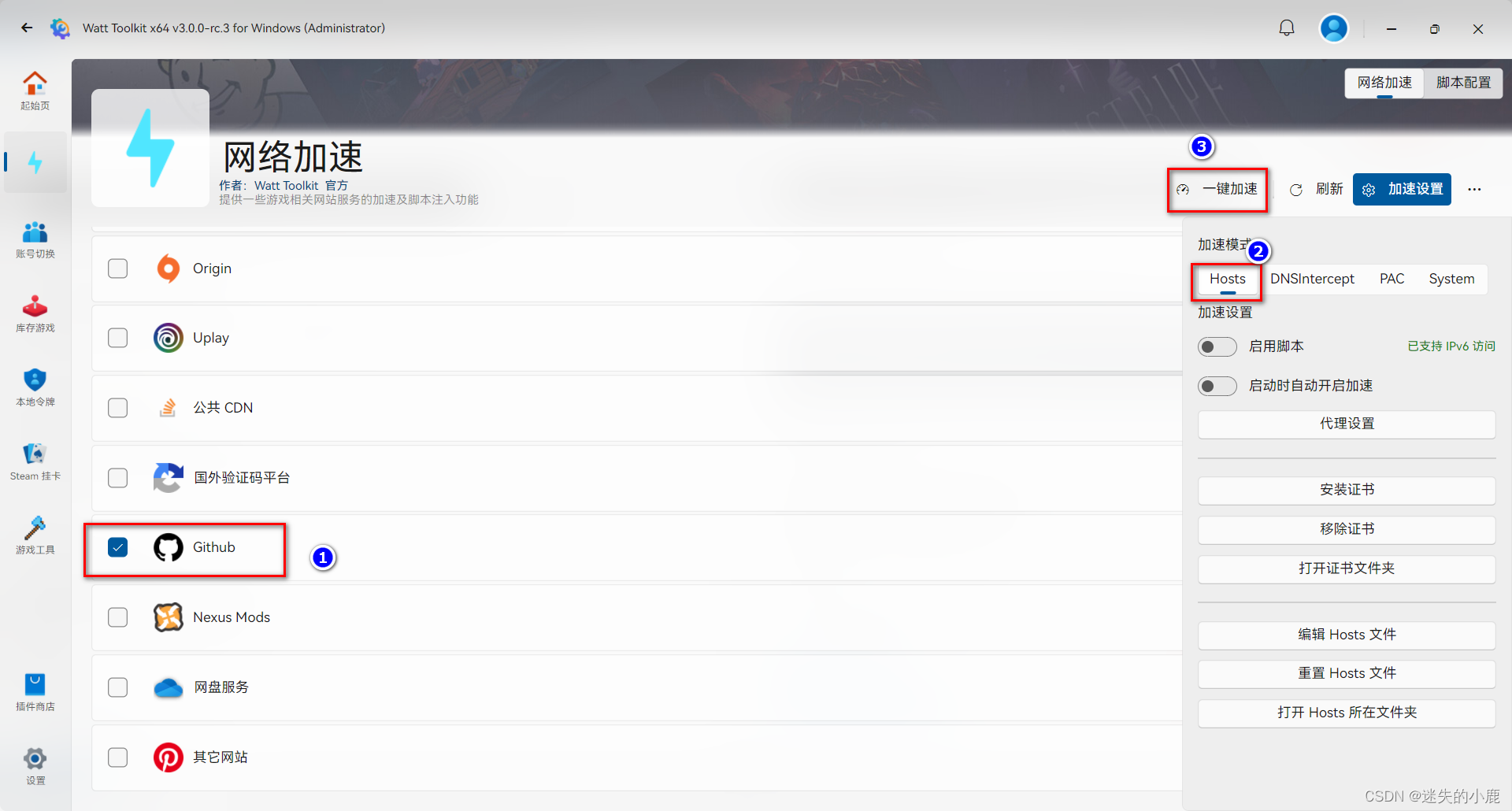
github连不上
github连不上 错误提示解决方案steam 采用Hosts加速 错误提示 fatal: unable to access ‘https://github.com/Ada-design/qianduan.git/’: Failed to connect to github.com port 443 after 21073 ms: Couldn’t connect to server 解决方案 下载steam https://steampp.ne…...

Excel计算表达式的值
Excel如何求解表达式 其中第三种方法最简单,通过剪贴板实现 如,单元格A1中输入了 12345 然后在A2输入 “”&A1 然后复制A2,打开剪贴板,点击刚才复制的内容,就会在A2显示计算结果...
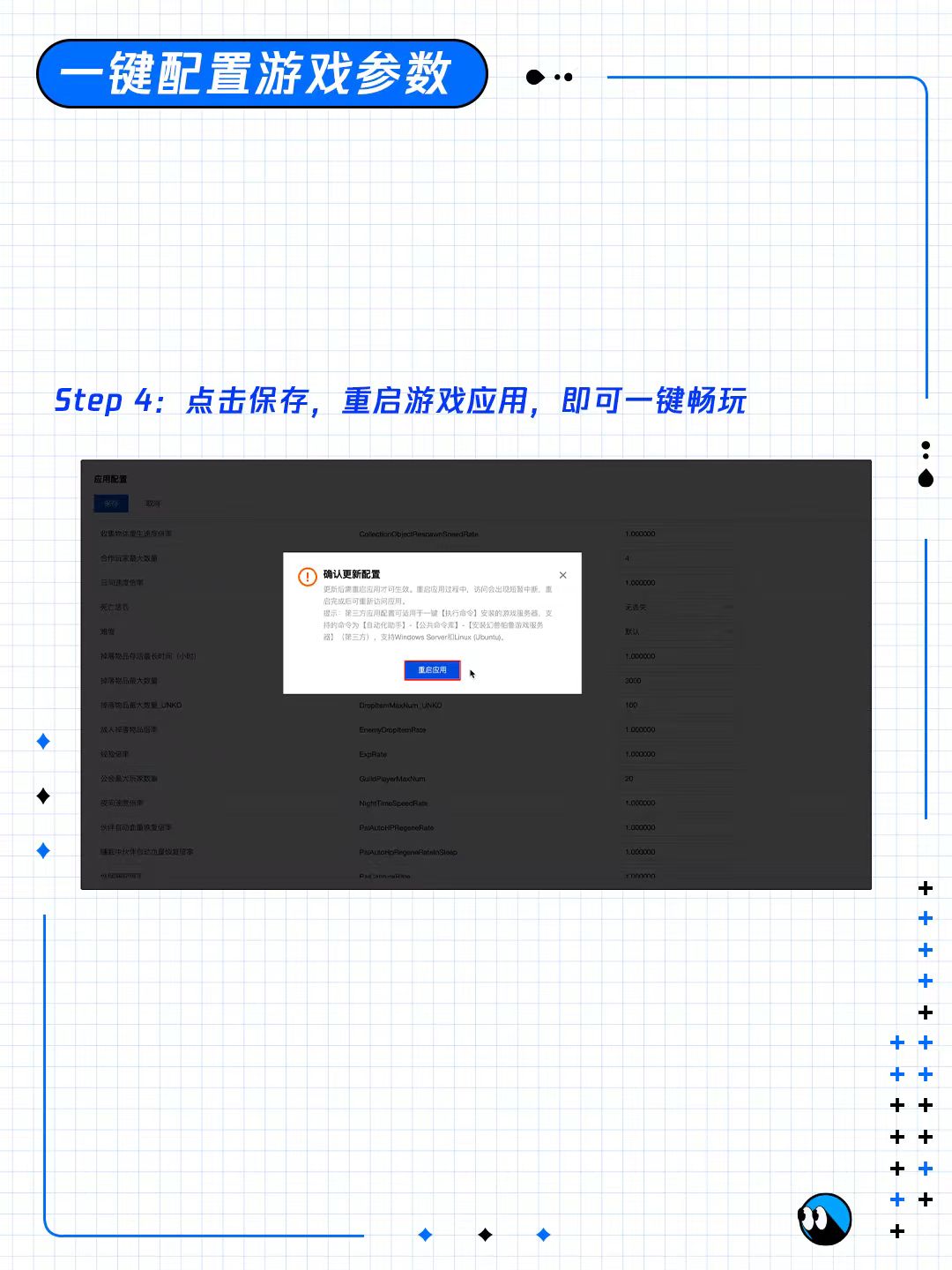
26元/月起!腾讯云一键自动搭建4核16G幻兽帕鲁服务器
腾讯云无需任何配置自动搭建幻兽帕鲁游戏联机服务器,游戏24小时在线,4核16G游戏联机服务器低至26元/月起,新手小白也能一键搭建属于自己的幻兽帕鲁游戏联机服务器! 第一步:购买游戏联机服务器 购买入口:htt…...

【C++游戏开发-01】推箱子
C游戏开发 文章目录 C游戏开发[TOC](文章目录) 前言一、逻辑分析1.1地图实现1.2人物的移动1.2.1小人移动1.2.2其他移动 1.3墙壁的碰撞1.4箱子的推动1.4.1什么时候推箱子1.4.2什么情况可以推箱子 1.5胜利的判断1.6卡关的处理1.7关卡的切换 二、DEMO代码2.1游戏框架2.2各功能函数…...
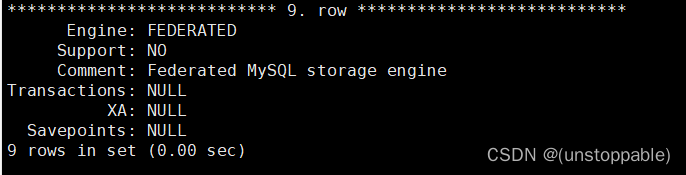
【lesson26】学习MySQL事务前的基础知识
文章目录 CURD不加控制,会有什么问题?CURD满足什么属性,能解决上述问题?什么是事务?为什么会出现事务事务的版本支持 CURD不加控制,会有什么问题? CURD满足什么属性,能解决上述问题&…...

持续积累分享金融知识
持续积累分享金融知识 一、什么是两融余额?二、什么是量化?三、散户可以进行量化投资么? 一、什么是两融余额? 两融余额是指投资者在融资买入和融券卖出交易中,通过向券商借入资金或证券进行交易,并且在交…...

网络协议 UDP协议
网络协议 UDP协议 在之前的文章中有对UDP协议套接字的使用进行讲解,本文主要对UDP协议进行一些理论补充。 文章目录 网络协议 UDP协议1. 概念2. UDP协议格式2.1 数据报长度2.2 校验和/检验和2.2.1 CRC校验2.2.2 MD5算法 1. 概念 UDP,即User Datagram P…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
