代码随想录刷题笔记 DAY 18 | 找树左下角的值 No.513 | 路经总和 No.112 | 从中序与后序遍历序列构造二叉树 No.106
Day 18
01. 找树左下角的值(No. 513)
题目链接
代码随想录题解
1.1 题目
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
示例 1:
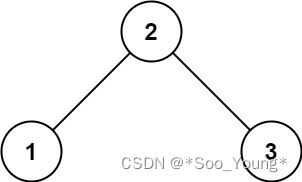
输入: root = [2,1,3]
输出: 1
示例 2:
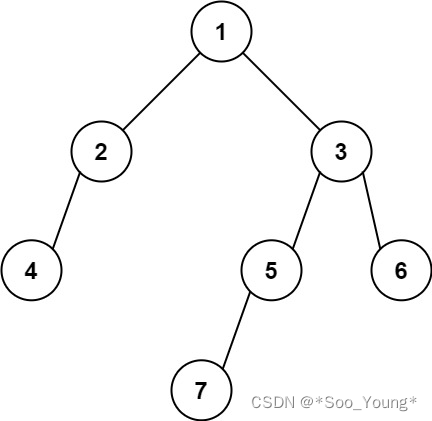
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7
提示:
- 二叉树的节点个数的范围是
[1,104] -231 <= Node.val <= 231 - 1
1.2 笔记
这道题递归实现很简单,但思路是比较难想到
根据这个题目中的 最底层 可以得到,无论是收集到的上一个节点多么靠左,如果有比它还深的节点,那这个节点更有可能是结果的节点。
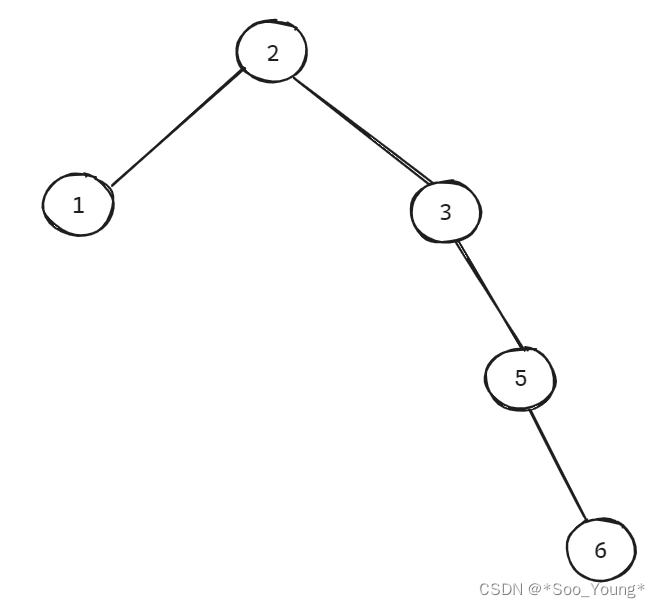
比如上图中,无论 1 节点多么靠左,这道题的答案仍然是 6,这也就导致了 最左边的节点不一定是左节点,递归向左的方式就被否定了。
但如果是同层的,因为采用的遍历顺序是 左中右 的顺序,同层的最左边一定是被最先遍历到的,所以对于同层的只需要拿到第一个即可。
这里定义一个类来存放节点的 深度 和 数值
class Node {int val;int floor;public Node(int val, int floor) {this.val = val;this.floor = floor;}
}
1.3 代码
class Solution {int floor = 0; // 记录当前节点的层数Node tempNode = new Node(0, 0);public int findBottomLeftValue(TreeNode root) {tempNode = new Node(root.val, 1);reverse(root);return tempNode.val;}public void reverse(TreeNode node) {if (node == null) {return;}floor++;// 说明本次遍历到的节点深度更深if (floor > tempNode.floor) {tempNode = new Node(node.val, floor);}reverse(node.left);reverse(node.right);floor--;}
}
/**记录可能是结果的节点的深度和值*/
class Node {int val;int floor;public Node(int val, int floor) {this.val = val;this.floor = floor;}
}
02. 路经总和(No. 112)
题目链接
代码随想录题解
2.1 题目
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
示例 1:
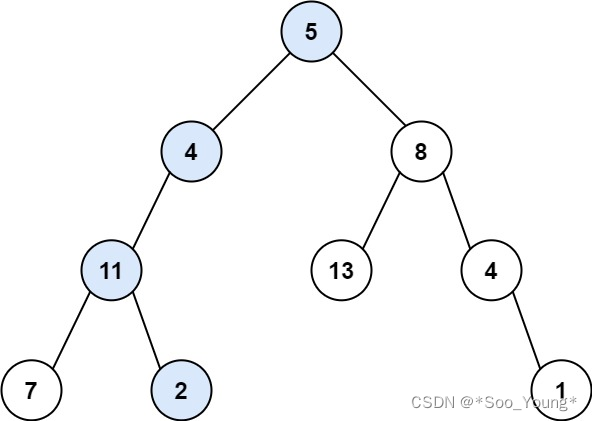
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
解释:等于目标和的根节点到叶节点路径如上图所示。
示例 2:
输入:root = [1,2,3], targetSum = 5
输出:false
解释:树中存在两条根节点到叶子节点的路径:
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。
示例 3:
输入:root = [], targetSum = 0
输出:false
解释:由于树是空的,所以不存在根节点到叶子节点的路径。
提示:
- 树中节点的数目在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
2.2 笔记
是一道非常简单的递归题目,和递归计算深度思路完全相同,但是本题计算的是总和。
但这道题目有一个很大的坑就是在剪枝上,剪枝到最后发现最好的方式是不要加任何剪枝操作
看一下能想到的剪枝的想法
当前总和大于目标值:推翻,因为有可能存在负数当目标值大于 0 时选大于,小于 0 时选小于:推翻,因为节点中可能存在负数
所以本题是无法加入剪枝操作的,对这些边缘处理一定要考虑好。
剩下的就是简单的递归处理了。
为了递归代码尽量的简洁,我将 targetSum 单独的抽离出来作为一个全局变量。
这道题在回顾一下递归要考虑的三个部分
- 递归的出口:
node = null因为对空节点的任何操作都是没有意义的,还有就是叶子节点,在叶子节点直接收集信息然后可以返回,直接返回的话要进行后续位置进行的操作,这里再详细的解释一下,看下面代码中判断叶子节点并且返回的位置,这个位置处于递归的前序位置,但是currentSum -= node.val是处于后序位置的,也就是说后续位置的操作还没有执行就直接返回了;当然,也可以选择不return,递归到下一层发现是空节点返回后同样也会执行后序位置的代码。 - 递归的返回值:因为这里采用外置全局变量的方式,是不需要任何返回值的。
- 递归中要进行的操作:拿取当前路径下的总和、判断是否符合结果的要求,分别向左向右递归,离开节点时删除节点的
val。
2.3 代码
class Solution {int currentSum = 0; // 记录总和boolean flg = false;int target;public boolean hasPathSum(TreeNode root, int targetSum) {target = targetSum;reverse(root);return flg;}public void reverse(TreeNode node) {if (node == null) {return;}currentSum += node.val;// 判断是否为叶子节点if (currentSum == target && node.right == null && node.left == null) {flg = true;return;}reverse(node.right);reverse(node.left);currentSum -= node.val;}
}
03. 从中序与后序遍历序列构造二叉树(No. 106)
题目链接
代码随想录题解
1.1 题目
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:
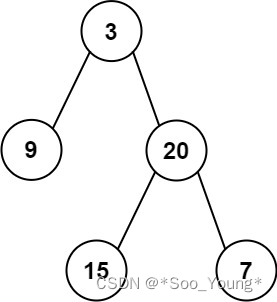
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1]
输出:[-1]
提示:
1 <= inorder.length <= 3000postorder.length == inorder.length-3000 <= inorder[i], postorder[i] <= 3000inorder和postorder都由 不同 的值组成postorder中每一个值都在inorder中inorder保证是树的中序遍历postorder保证是树的后序遍历
1.2 笔记
后序遍历的顺序是 左 右 中
中序遍历的顺序是 左 中 右
先来看一下为什么仅仅通过一个遍历得不到完整的二叉树,而需要两个遍历配合
这就导致了这两种遍历形成的数组是这样的:

后序的最后一个位置的节点一定是中心节点,但是这个节点的左子树和右子树是混合在左边的,再来看中序遍历,虽然它的左右子树是分开的,但是中心节点不得而知,所以需要两个遍历顺序配合来解题。
通过上面的规律,可以总结出一个大概的解题思路:
- 从后序拿到中心节点
- 在中序中找到中心节点
- 分割中序数组,可以得到左子树的所有节点和右子树的所有节点
- 通过分割完成的两个中序数组的长度来切割后序的数组
- 构造当前的节点,也就是后序的最后一个元素
- 以新的中序数组和新的后序数组再次执行上述的步骤,直到只剩下一个节点
这个思路就需要通过递归来完成
简单的画一个图
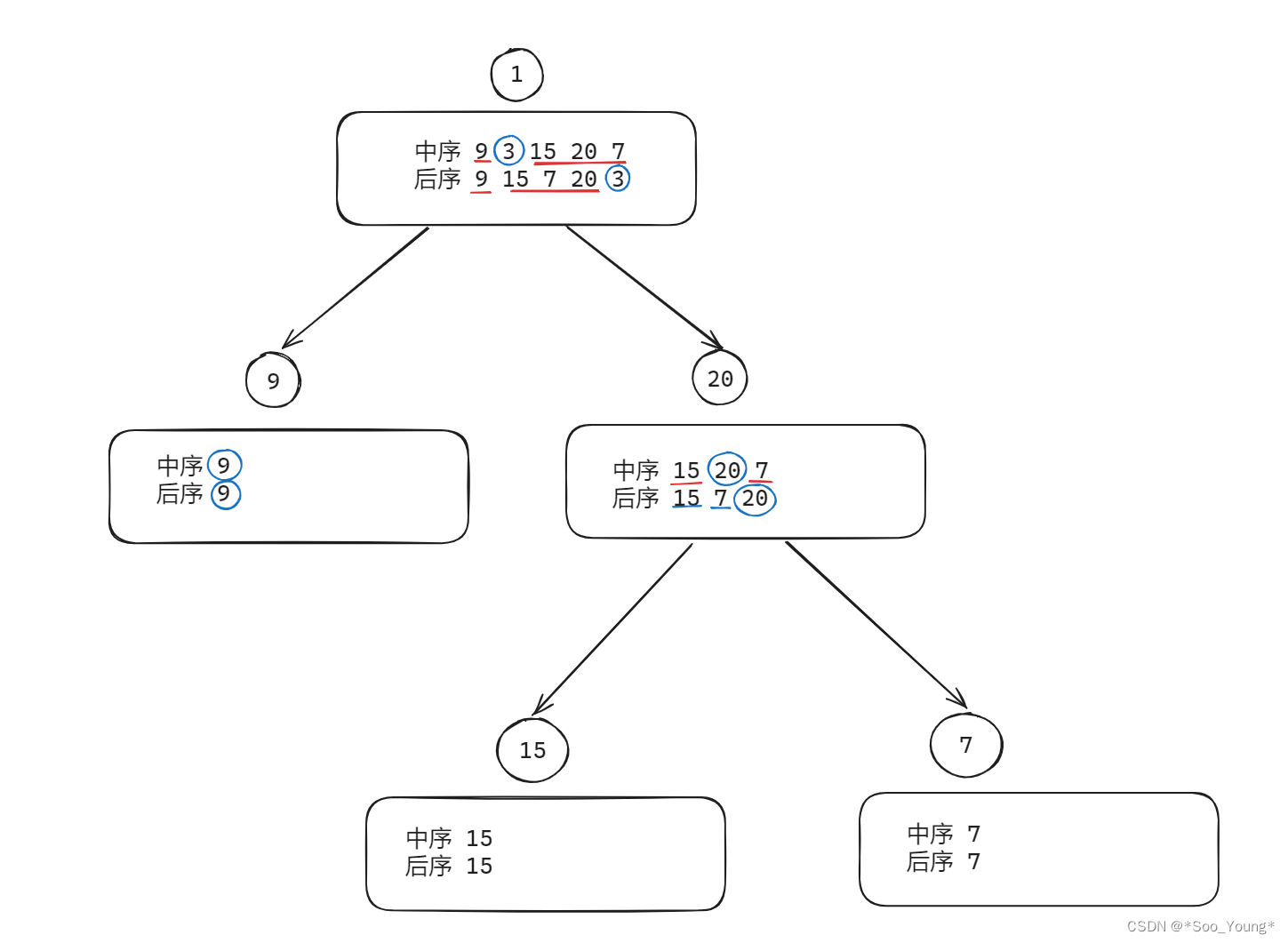
通过这样逐次的递归,会在后序数组和中序数组长度为 1 的时候就是递归结束的时候,这时候创建节点直接返回即可
再来看每次递归中要做的事情:
- 递归的出口,数组为
null也就是传入数据为空的时候直接返回空;当数组的长度为1的时候,比如上图的9节点,意味着遍历到叶子节点了,这时候也直接返回。 - 递归返回值:因为要构建二叉树,返回的内容是一个节点,使得返回的这个节点树称为上一个节点的子树。
- 每次递归要进行的内容:判断是否符合返回条件、执行上面的六个步骤、返回该节点
3.3 代码
class Solution {public TreeNode buildTree(int[] inorder, int[] postorder) {return reverse(inorder, postorder);}public TreeNode reverse(int[] inorder, int[] postorder) {if (postorder.length == 0) {return null;}if (postorder.length == 1) {// 叶子节点return new TreeNode(postorder[0]);}int target = postorder[postorder.length - 1]; // 拿到节点的值int index = 0;for (int i = 0; i < inorder.length; i++) {if (inorder[i] == target) {index = i; // 记录切割节点的值break;}}// 切割中序数组,copyOfRange 为左闭右开int[] newInorderLeft = Arrays.copyOfRange(inorder, 0, index); // 左int[] newInorderRight = Arrays.copyOfRange(inorder, index + 1, inorder.length); // 右// 切割后序数组int[] newPostorderLeft = Arrays.copyOfRange(postorder, 0, newInorderLeft.length);int[] newPostorderRight = Arrays.copyOfRange(postorder, newInorderLeft.length, postorder.length-1);TreeNode node = new TreeNode(target);node.left = reverse(newInorderLeft, newPostorderLeft);node.right = reverse(newInorderRight, newPostorderRight);return node;
3.4 补充
上述的代码中不断的进行数组的切割,会导致时间复杂度很高,这里可以使用逻辑切割,也就是通过传入数组的 startIndex 和 endIndex 来限制数组的空间。
这时候递归的出口就变成了
startIndex == endIndex || startIndex > endIndex
后一个条件是为了处理空的情况,如果带入空值会让数组下标出现负数,可以调试试一下
还需要修改的是下面传入的内容,书写的时候可以把当前的数组写出来,比如起始位置不要写 0 而要写 startIndex,这样可以避免书写条件的时候出错
node.left = reverse(inorderStart, index-1, postorderStart, postorderStart+(index- inorderStart-1));
node.right = reverse(index+1, inorderEnd, postorderStart+(index-inorderStart), postorderEnd-1);
最终写出的条件是这样的,总体的思路和上面的代码相同
class Solution {int[] globalInorder;int[] globalPostOrder;public TreeNode buildTree(int[] inorder, int[] postorder) {globalInorder = inorder;globalPostOrder = postorder;return reverse(0, inorder.length-1, 0, postorder.length-1);}public TreeNode reverse(int inorderStart, int inorderEnd, int postorderStart, int postorderEnd) {if (postorderStart > postorderEnd) {return null;}if (postorderEnd == postorderStart) {// 叶子节点return new TreeNode(globalPostOrder[postorderStart]);}int target = globalPostOrder[postorderEnd]; // 拿到节点的值int index = 0;for (int i = inorderStart; i <= inorderEnd; i++) {if (globalInorder[i] == target) {index = i; // 记录切割节点的值,也就是此时的节点break;}}TreeNode node = new TreeNode(target);node.left = reverse(inorderStart, index-1, postorderStart, postorderStart+(index-inorderStart-1));node.right = reverse(index+1, inorderEnd, postorderStart+(index-inorderStart), postorderEnd-1);return node;}
}
相关文章:

代码随想录刷题笔记 DAY 18 | 找树左下角的值 No.513 | 路经总和 No.112 | 从中序与后序遍历序列构造二叉树 No.106
Day 18 01. 找树左下角的值(No. 513) 题目链接 代码随想录题解 1.1 题目 给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。 假设二叉树中至少有一个节点。 示例 1: 输入: root [2,1,3] 输出: 1 示例 2: 输入…...
【algorithm】一个简单的PID工程 base 用于手生时候快速复习 用于设计模式 cpp语法八股 快速复习校验
写在前面 最近项目一直用matlab,防止手生整一个回忆工具使用的简单的pid demo,走一边流程,包括配工程debug看结果,复用之前记录的配置见我的bloghttps://blog.csdn.net/weixin_46479223/article/details/135082867?csdn_share_t…...

Python处理图片生成天际线(2024.1.29)
1、天际线简介 天际线(SkyLine)顾名思义就是天空与地面的边界线,人站在不同的高度,会看到不同的景色和地平线,天空与地面建筑物分离的标记线,不得不说,每天抬头仰望天空,相信大家都可…...

jsp服装穿搭推荐系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 JSP 游戏网上商城系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为 TOMCAT7.0,Myeclipse8.5开发,数据库为Mysql5.0…...
Opencv(C++)学习 之RV1126平台的OPENCV交叉编译
本文特点:网上已经有了很多opencv移植RV1106的文章,本文主要记录基于cmake-gui编译,碰到的报错,及解决报错问题的方法,同时简单总结一些配置项相关的知识。 一、环境: ubuntu18 x64 RV1126交叉编译工具链 …...

http和https区别
HTTP协议以明文方式发送内容,不提供任何方式的数据加密。HTTP协议不适合传输一些敏感信息,比如:信用卡号、密码等支付信息。https则是具有安全性的ssl加密传输协议。http和https使用的是完全不同的连接方式,用的端口也不一样&…...
富文本编辑器CKEditor4简单使用-05(开发自定义插件入门)
富文本编辑器CKEditor4简单使用-05(开发自定义插件入门) 1. CKEditor4插件入门1.1 关于CKEditor4插件的简单安装与使用1.2 参考 2. 开发自定义插件——当前时间插件2.1 创建插件文件目录结构2.2 编写插件原代码2.2.1 编写代码框架2.2.2 创建编辑器命令2.…...

chisel之scala 语法
Chisel新手教程之Scala语言(1) Value & variable Value是immutable的,当它被分配一个数据后,无法进行重新分配。用 val 表示。 Variable是mutable的,可以重复赋值。用 var 表示。示例如下: val a …...
React18构建Vite+Electron项目以及打包
一.先创建项目 cnpm create vite 选择React > JavaScript >cd react_vite > cnpm i >npm run dev 二.安装Electron依赖 指定版本相对稳定 cnpm i electron19.0.10 -D cnpm i vite-plugin-electron0.9.3 -D cnpm i electron-builder23.0.1 -D三.创建electron目录…...

Spark性能调优
Spark性能调优 executor内存不足用UNION ALL代替UNIONpersist与耗时监控用OR替换UNION ALL用JOIN替换IN executor内存不足 问题表现1:Container xx is running beyond physical memory limits. Current usage: xxx GB of x GB physical memory used; xx GB of x GB…...

flutter开发实战-Camera自定义相机拍照功能实现
flutter开发实战-Camera自定义相机拍照功能实现 一、前言 在项目中使用image_picker插件时候,在android设备上使用无法默认设置前置摄像头(暂时不清楚什么原因),由于项目默认需要使用前置摄像头,所以最终采用自定义…...
LeetCode15. 三数之和
15. 三数之和 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 **注意:**答案中不可以包含重复…...
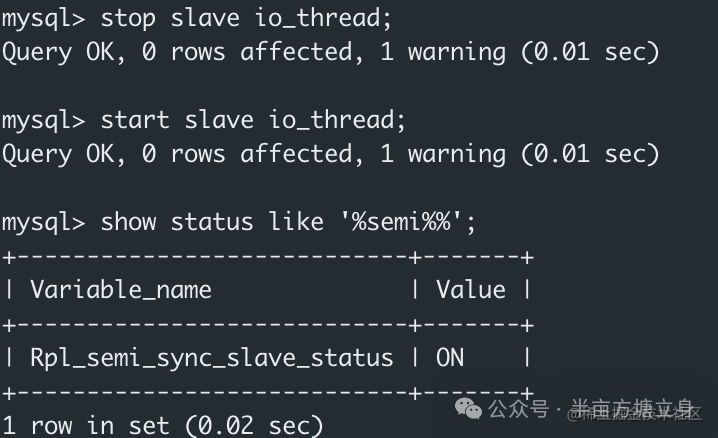
Docker搭建MySQL8主从复制
之前文章我们了解了面试官:说一说Binlog是怎么实现的,这里我们用Docker搭建主从复制环境。 docker安装主从MySQL 这里我们使用MySQL8.0.32版本: 主库配置 master.cnf //基础配置 [client] port3306 socket/var/run/mysqld/mysql.sock [m…...

【前端】日期转换
记录项目中需要处理的日期格式 默认vue2 初级版 将后端传来的数组 [2024/01/29 08:55:18, 2024/01/29 09:55:18, 2024/01/29 10:11:18]转为 [2024-01-29 08:55, 2024-01-29 09:55, 2024-01-29 10:11]方法 convertDateTimeFormat(arr) {var tempArr arr.map(function (dateT…...

Git 怎么设置用户的权限
在团队协作的软件开发中,对于版本控制系统Git来说,确保代码与数据的安全性至关重要。为了实现这一目标,Git提供了灵活且可定制的用户权限管理机制。下面将简单的探讨一下Git如何设置用户的权限,以及如何保护代码和数据。 用户身份…...

大端和小端模式介绍
介绍 “大端”和“小端”通常指的是字节序(Byte Order)的两种类型,也被称为端序(Endianness)。在多字节的数据类型(如整数)中,字节可以以不同的顺序存储,这影响了计算机…...
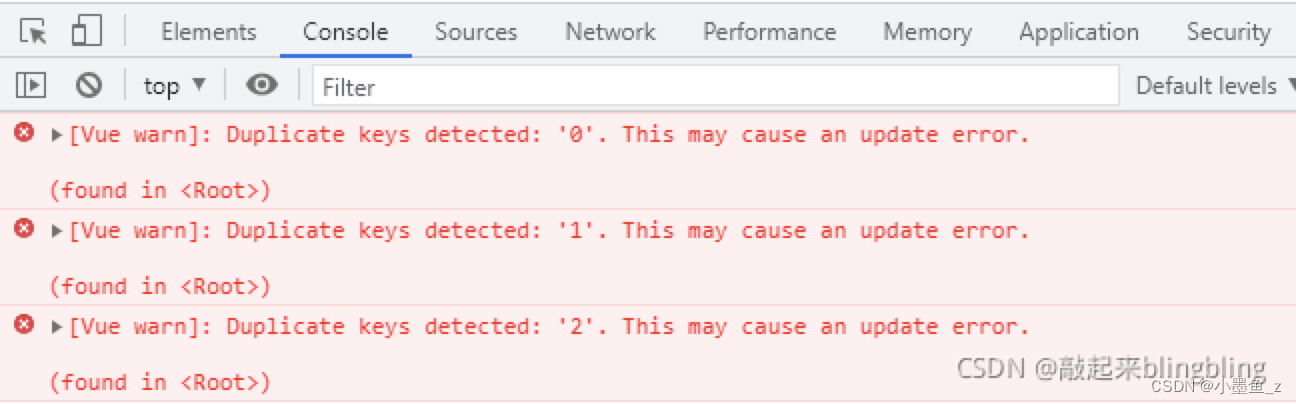
【vue】报错 Duplicate keys detected 解决方案
错误描述:Duplicate keys detected. This may cause an update error.错误直译:检测到重复的键。这可能会导致错误。错误原因:有相同父元素的多个子元素的v-for有相同的key值。 解决方法: return:{dataList:[{name:张三…...
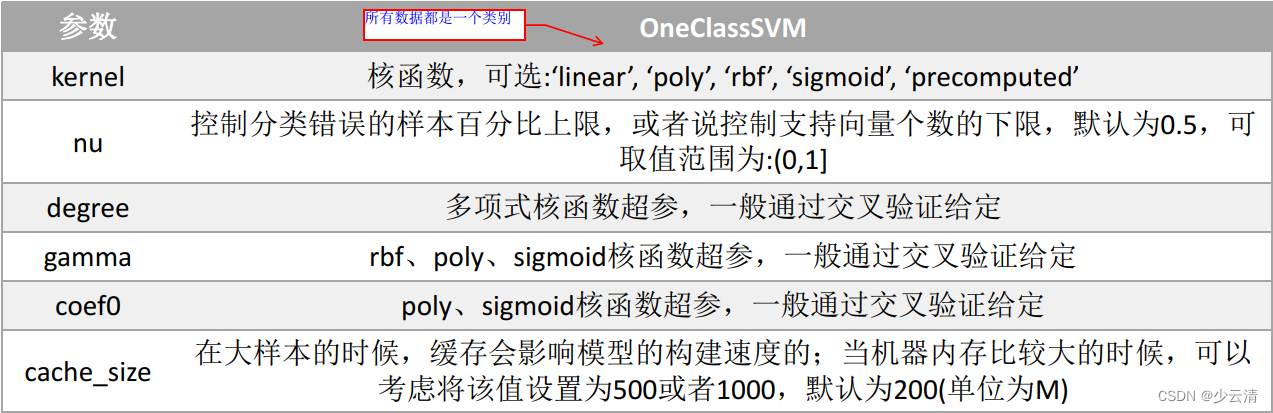
机器学习_13_SVM支持向量机、感知器模型
文章目录 1 感知器模型1.1 感知器的思想1.2 感知器模型构建1.3 损失函数构建、求解 2 SVM3 线性可分SVM3.1 线性可分SVM—概念3.2 线性可分SVM —SVM 模型公式表示3.3 线性可分SVM —SVM 损失函数3.4 优化函数求解3.5 线性可分SVM—算法流程3.6 线性可分SVM—案例3.7 线性可分S…...

OpenCV学习记录——轮廓检测
文章目录 前言一、寻找、绘制轮廓二、具体应用代码 前言 寻找目标图像的轮廓并绘制出该轮廓是我们进行图像识别时常用的手段,轮廓是图像中连续的边界线,可以用于物体检测、形状分析等应用。为了获取更高的准确性,会先进行二值化处理ÿ…...

FreeRTOS任务挂起以及延时部分源码分析
layout: post title: “任务状态” date: 2023-7-19 15:39:08 0800 tags: FreeRTOS 任务状态 fireRTOS代码分析 任务挂起 //把一个任务挂起 void vTaskSuspend( TaskHandle_t xTaskToSuspend ) {TCB_t *pxTCB;taskENTER_CRITICAL();//进入临界区{/* 参数是NULL的时候设置为当…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...
