C++ 动态规划 线性DP 最长共同子序列
给定两个长度分别为 N
和 M
的字符串 A
和 B
,求既是 A
的子序列又是 B
的子序列的字符串长度最长是多少。
输入格式
第一行包含两个整数 N
和 M
。
第二行包含一个长度为 N
的字符串,表示字符串 A
。
第三行包含一个长度为 M
的字符串,表示字符串 B
。
字符串均由小写字母构成。
输出格式
输出一个整数,表示最大长度。
数据范围
1≤N,M≤1000
输入样例:
4 5
acbd
abedc
输出样例:
3
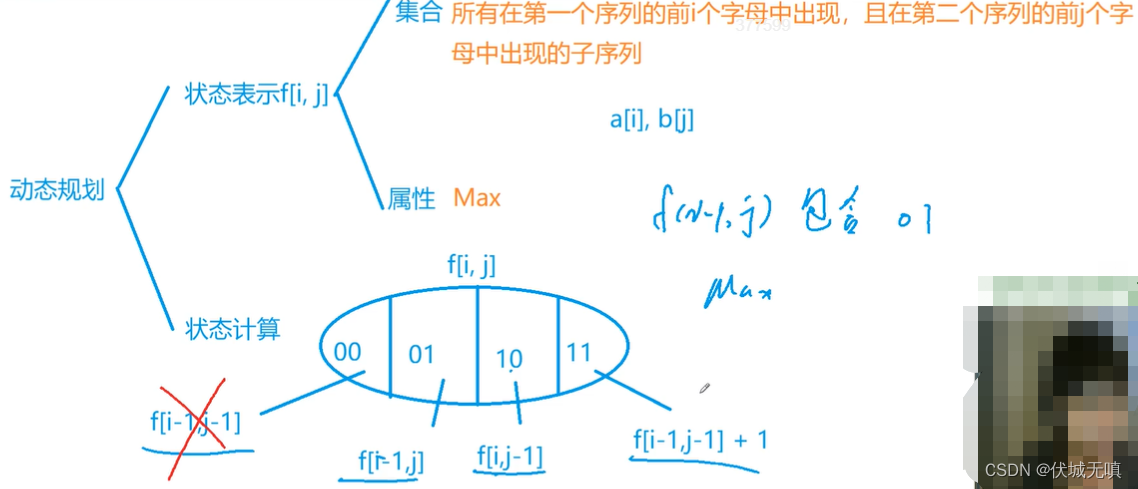
#include <iostream>
#include <algorithm>using namespace std;const int N = 1010;
char a[N], b[N];
int f[N][N];
int n, m;int main ()
{cin>>n>>m;scanf("%s%s", a + 1, b + 1);for(int i = 1; i <= n; i ++ )for(int j = 1; j <= m; j ++ ){f[i][j] = max(f[i - 1][j], f[i][j - 1]);if(a[i] == b[j])f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);}cout<<f[n][m]<<endl;return 0;
}
相关文章:

C++ 动态规划 线性DP 最长共同子序列
给定两个长度分别为 N 和 M 的字符串 A 和 B ,求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。 输入格式 第一行包含两个整数 N 和 M 。 第二行包含一个长度为 N 的字符串,表示字符串 A 。 第三行包含一个长度为 M 的字符串,表…...

【备战蓝桥杯】——循环结构终篇
🌈个人主页: Aileen_0v0 🔥热门专栏: 华为鸿蒙系统学习|计算机网络|数据结构与算法 💫个人格言:“没有罗马,那就自己创造罗马~” #mermaid-svg-yl4Tqejg4LkjZLAM {font-family:"trebuchet ms",verdana,arial,sans-serif;font-siz…...

为什么说Python语法简单?
Python被广泛认为是一种语法简单、易学易用的编程语言,这种观点有几个关键的原因: 1、清晰简洁的语法结构: Python采用了清晰而简洁的语法结构,使得代码易于阅读和理解。Python的语法设计强调代码的可读性,采用了清晰…...

【HarmonyOS应用开发】ArkUI 开发框架-进阶篇-管理组件状态(九)
管理组件状态 一、概述 在应用中,界面通常都是动态的。下图所示,在子目标列表中,当用户点击目标一,目标一会呈现展开状态,再次点击目标一,目标一呈现收起状态。界面会根据不同的状态展示不一样的效果。 Ar…...
EF Core入门例子(以SqLite为数据库)
测试环境: visual studio 2017 .net core 2.1 具体步骤如下: 1 新增名称为EFCoreDemo的.net core控制台程序,版本选择.net core 2.1,项目不能放到带中文的目录下,不然到后面执行Add-Migration命令时会报如下的错误…...

centos7 安装nginx
在 CentOS 7 上安装 Nginx,你可以选择从官方仓库(EPEL)安装,或者手动编译安装。以下是通过 EPEL 安装 Nginx 的步骤: 方法一:通过 EPEL 仓库安装 添加 EPEL 仓库: sudo yum install epel-relea…...
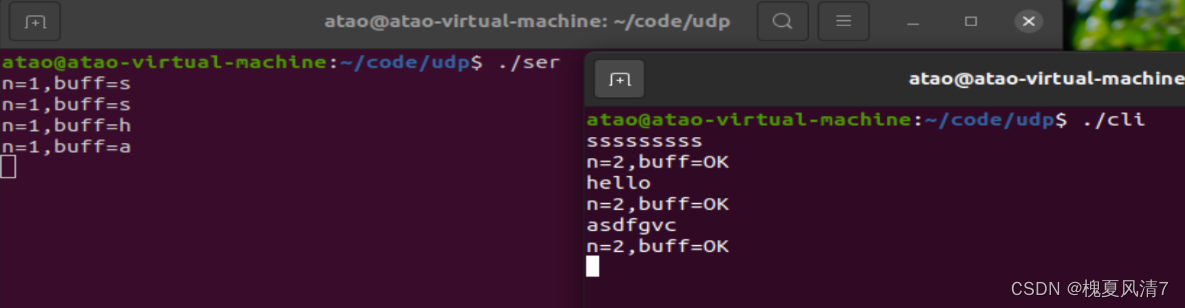
【Linux Day14 UDP网络通讯】
UDP网络通讯 UDP报文结构: 16位源端口:用于记录发送端的端口号(占用两个字节)16位目的端口:用于记录接收端的端口号(占用两个字节)16位UDP长度:确定UDP报文总长度,&…...

指针的深入了解6
1.回调函数 回调函数就是一个通过函数指针调用的函数。 如果你把函数的指针(地址)作为参数传递给另一个函数,当这个指针被用来调用其所指向的函数 时,被调用的函数就是回调函数。回调函数不是由该函数的实现方直接调用࿰…...

PHP之PDO_MYSQL扩展安装步骤
1,如果有php源码包可以不用下载,在 源码包下的 ext/ 下面可以找到 cd php-8.1.9/ext/pdo_mysql 2,如果存在,直接安装 /usr/local/php-8.1.9/bin/phpize ./configure --with-php-config/usr/local/php-8.1.9/bin/php-config make &&a…...
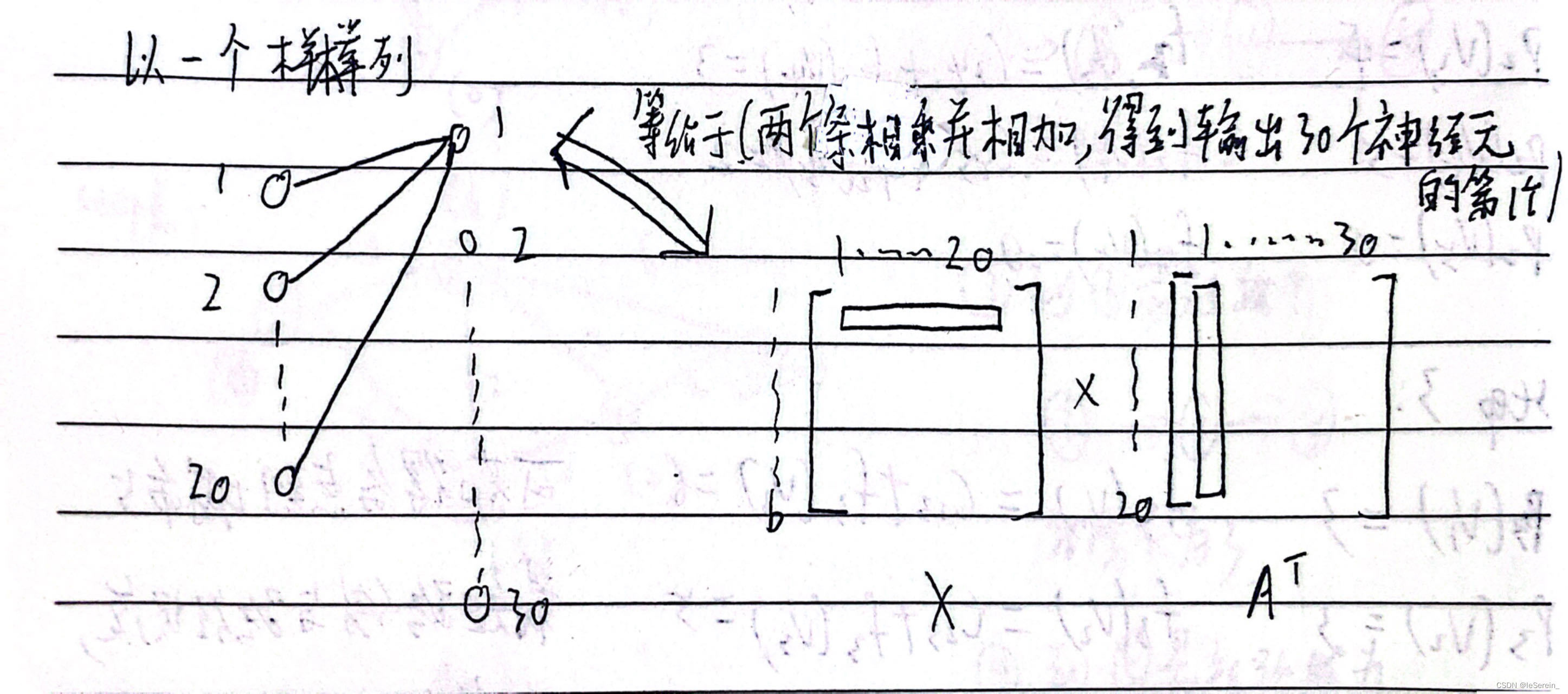
【pytorch】nn.linear 中为什么是y=xA^T+b
我记得读教材的时候是yWxb, 左乘矩阵W,这样才能表示线性变化。 但是pytorch中的nn.linear中,计算方式是yxA^Tb,其中A是权重矩阵。 为什么右乘也能表示线性变化操作呢?因为pytorch中,照顾到输入是多个样本一起算的&…...

vite打包原理
vite 工程化开发:打包工具 启动速度很快 核心原理还是webpack 把webpack封装了,把webpack对象封装了 和vue2整体结构几乎一致 webpack两种模式:开发&生产 代码打包编译,本地起一个web服务器实时预览编译后的结果 build 命令模…...
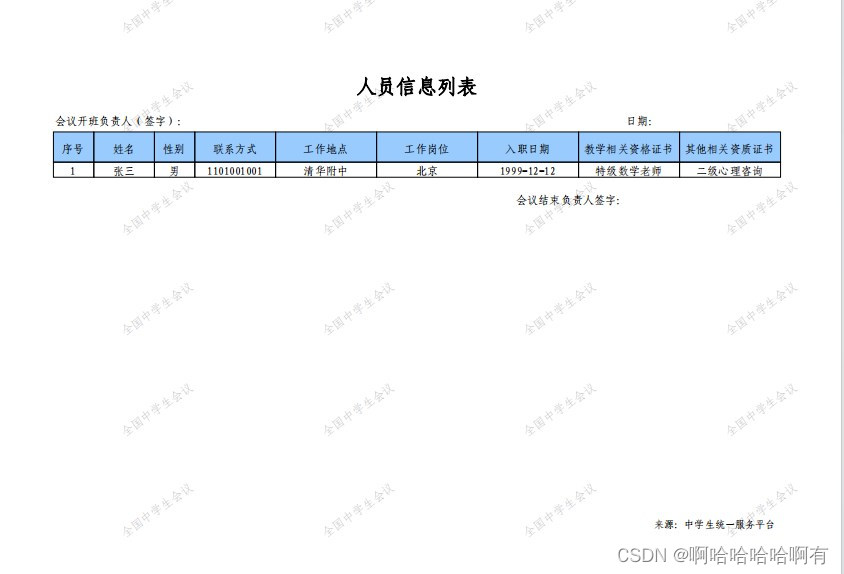
导出pdf 加密、加水印、加页脚
1.依赖 <dependency> <groupId>com.itextpdf</groupId> <artifactId>itextpdf</artifactId> <version>5.5.10</version> </dependency> <dependency> …...

Flutter 仿抖音 TikTok 上下滑动 播放视频
Flutter 仿抖音 TikTok 上下滑动 播放视频UI框架,视频播放使用 video_player github:GitHub - PangHaHa12138/TiktokVideo: Flutter 仿抖音 TikTok 上下滑动 播放视频UI框架 实现功能: 1.上下滑动自动播放切换视频,loading 封面…...

计算机网络——网络层(2)
计算机网络——网络层(2) 小程一言专栏链接: [link](http://t.csdnimg.cn/ZUTXU)前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家, [跳转到网站](https://www.captainbed.…...

01-16Maven-SpringBoot入门
Maven继承Maven高级SpringSpringBoot入门 Maven 一、概念及功能 概念:Maven是Apache软件基金会组织维护的一款专门为Java项目提供项目构建和依赖管理的工具 1.1作用: 项目构建 构建:是一个将代码从开发阶段到生产阶段的一个过程…...
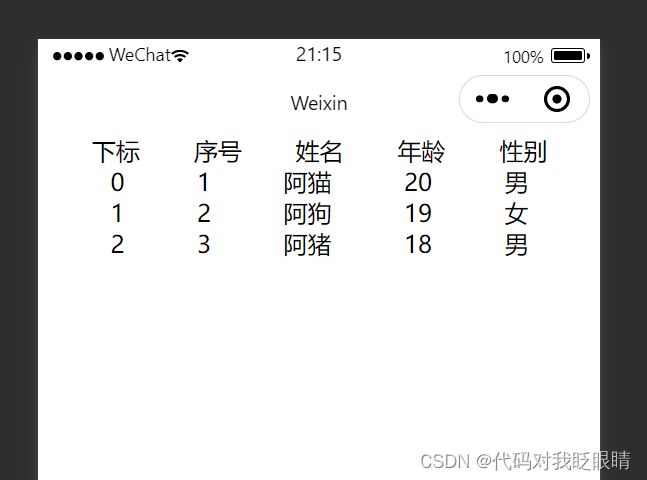
微信小程序(二十七)列表渲染改变量名
注释很详细,直接上代码 上一篇 新增内容: 1.改变默认循环单元item变量名 2.改变默认循环下标index变量名 基础模板有问题可以先看上一篇 源码: index.wxml <view class"students"><view class"item"><te…...
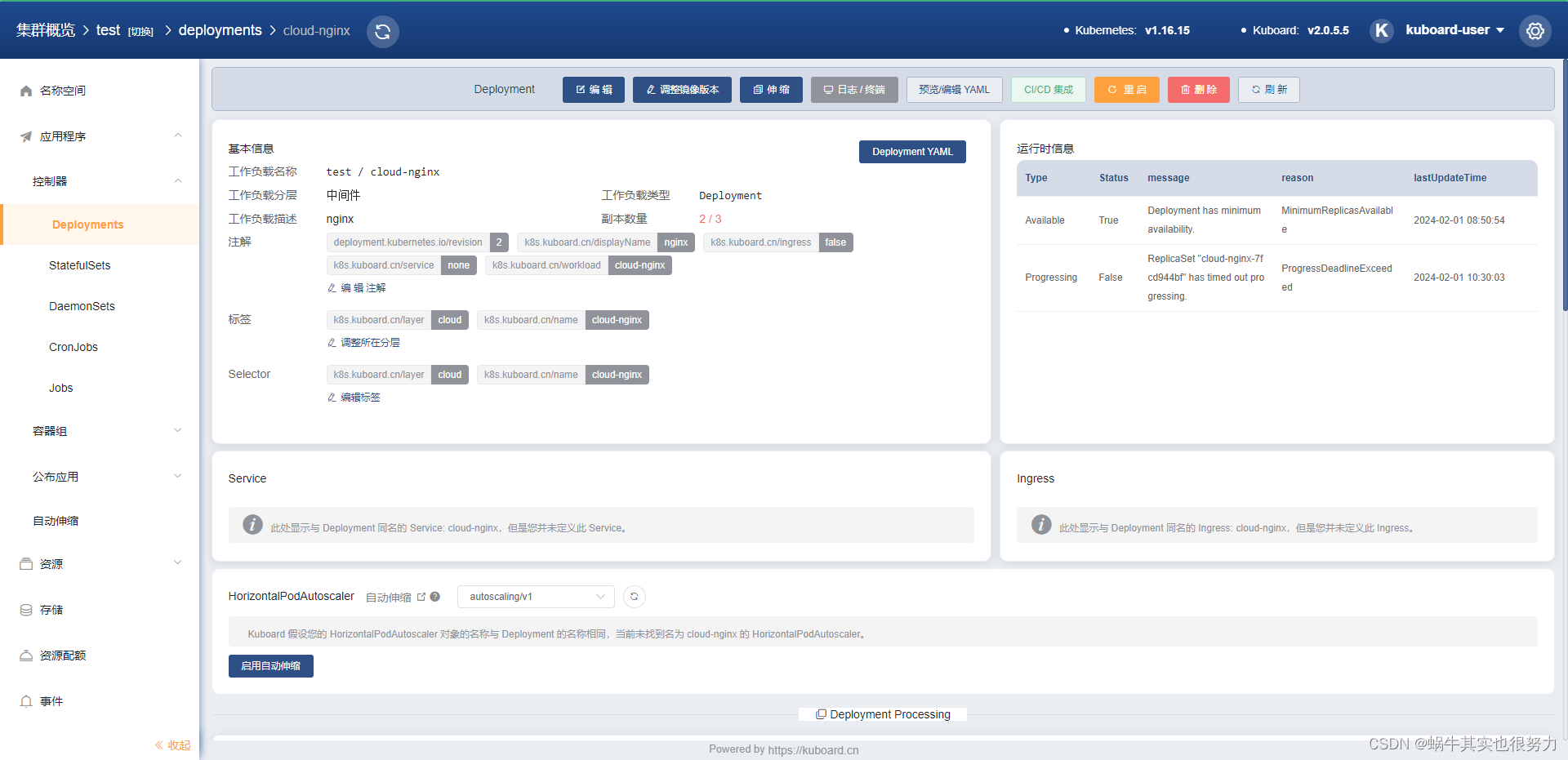
k8s之安装部署及kuboard发布应用
目录 环境准备 系统规划 配置免密 将桥接的IPv4流量传递到iptables的链 系统基础配置 安装docker 安装docker及基础依赖 配置docker的仓库下载地址 部署k8s 添加阿里云的k8s源 安装kubeadm,kubelet和kubectl 初始化masteer节点 部署node节点 部署flanne…...
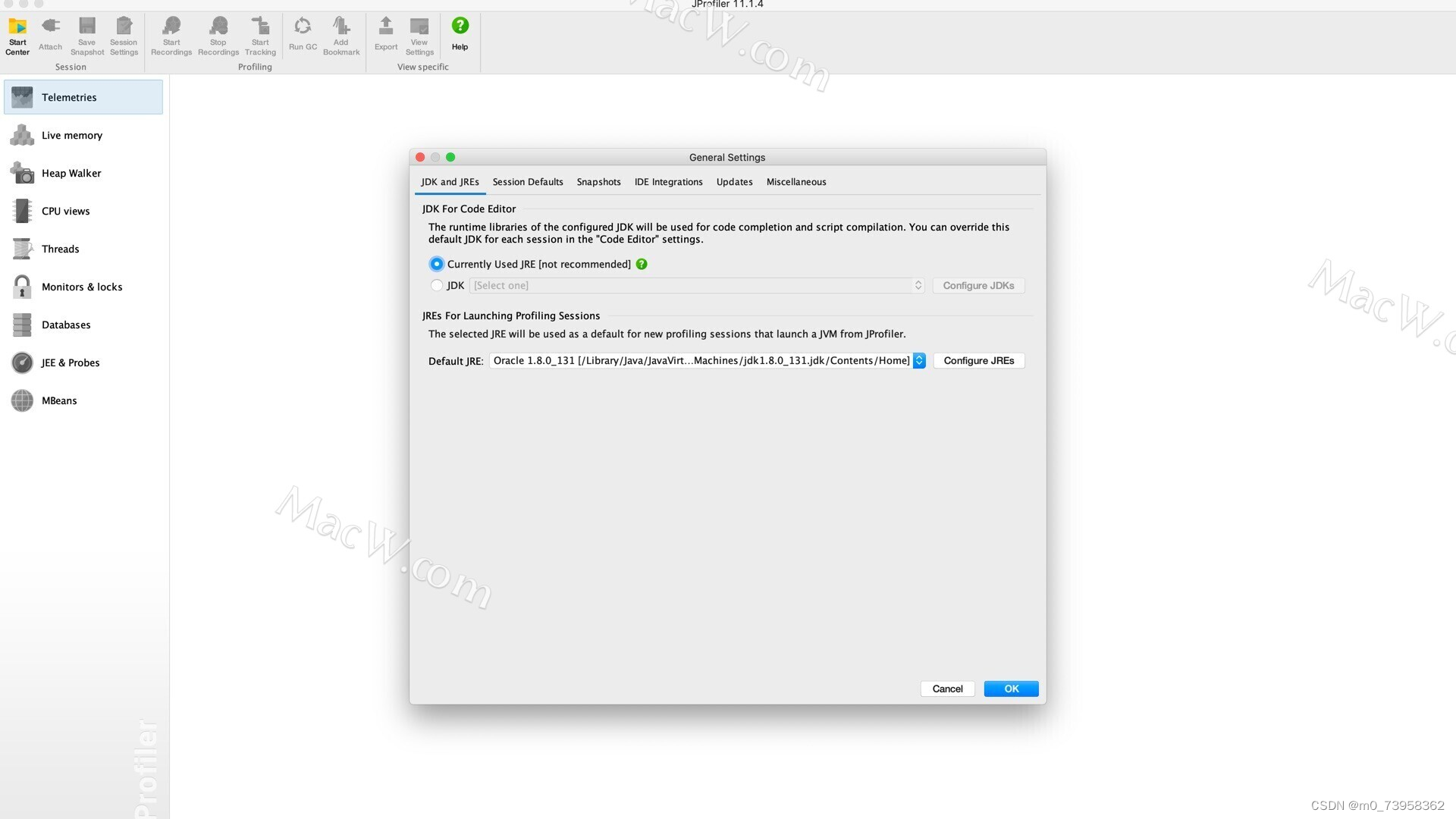
JProfiler for Mac:提升性能和诊断问题的终极工具
在当今的高性能计算和多线程应用中,性能优化和问题诊断是至关重要的。JProfiler for Mac 是一个强大的性能分析工具,旨在帮助开发者更好地理解其应用程序的运行情况,提升性能并快速诊断问题。 JProfiler for Mac 的主要特点包括:…...

力扣202-快乐数
快乐数 题目链接 解题思路: 两个指针,一快一慢,如果相遇,就会生成环如果环内元素为1,那么就可以返回 class Solution { public:int get(int n){int res 0;while(n){res (n%10) * (n%10);n / 10;}return res;}bool isHappy(int …...

牛客寒假训练营H题
思路:找出所有m的子集,加到价值中,找出最大价值即可。 代码: void solve(){int n, m;cin >> n >> m;vector<pii>a(n 1);for(int i 1;i < n;i )cin >> a[i].first >> a[i].second;int ans 0…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...
