【pytorch】nn.linear 中为什么是y=xA^T+b
我记得读教材的时候是y=Wx+b, 左乘矩阵W,这样才能表示线性变化。
但是pytorch中的nn.linear中,计算方式是y=xA^T+b,其中A是权重矩阵。
为什么右乘也能表示线性变化操作呢?因为pytorch中,照顾到输入是多个样本一起算的(第一个维度是多个样本数,所以输入默认是行向量),所以用y=xA^T+b,输出的y也是行向量。
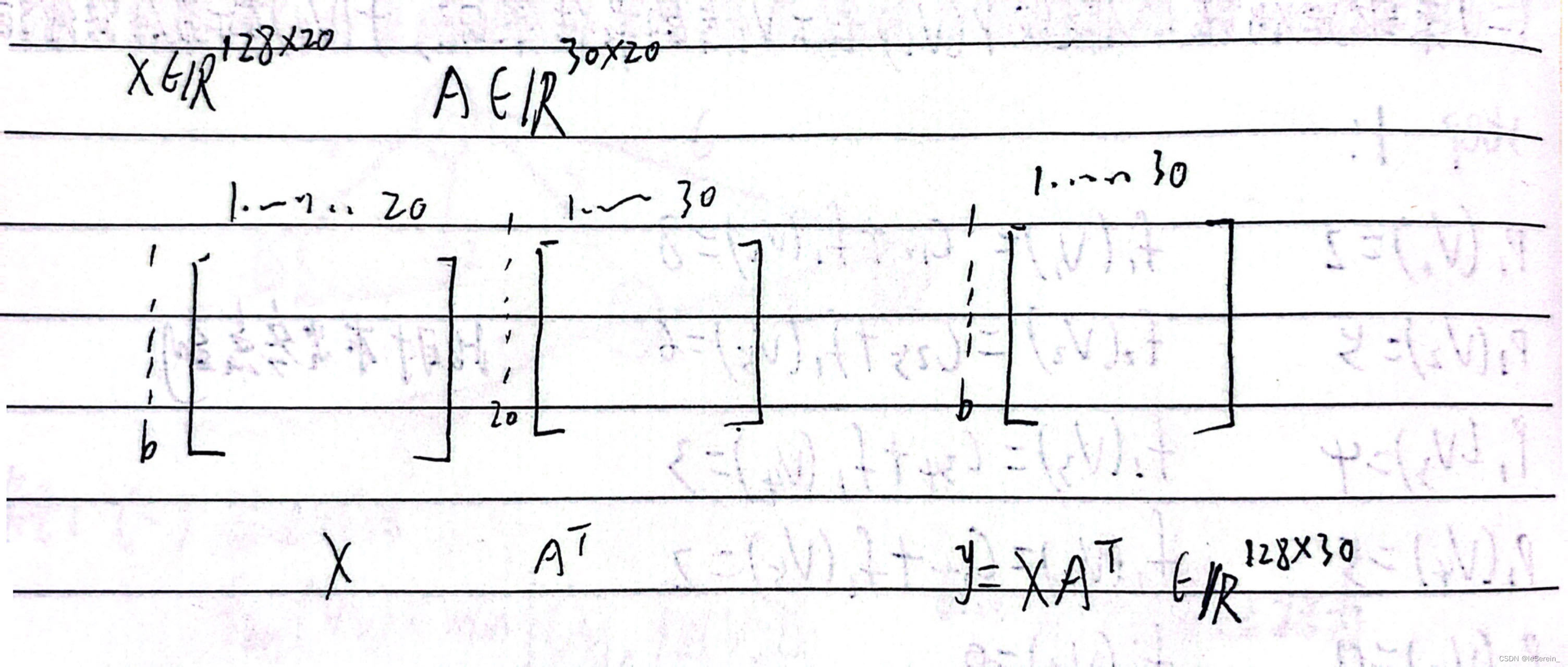
我们的教材中默认输入是列向量的,而pytorch为了用户方便,输入当作列向量,维度为(batch, dim),每行是特征
m = nn.Linear(20, 30)
input = torch.randn(128, 20)
output = m(input)print(output.size())
>>> torch.Size([128, 30])
print(m.weight.shape)
>>>torch.Size([30, 20]) # 注意这里的权重维度
我们再看一张图片,理解一下代码中的实现逻辑:
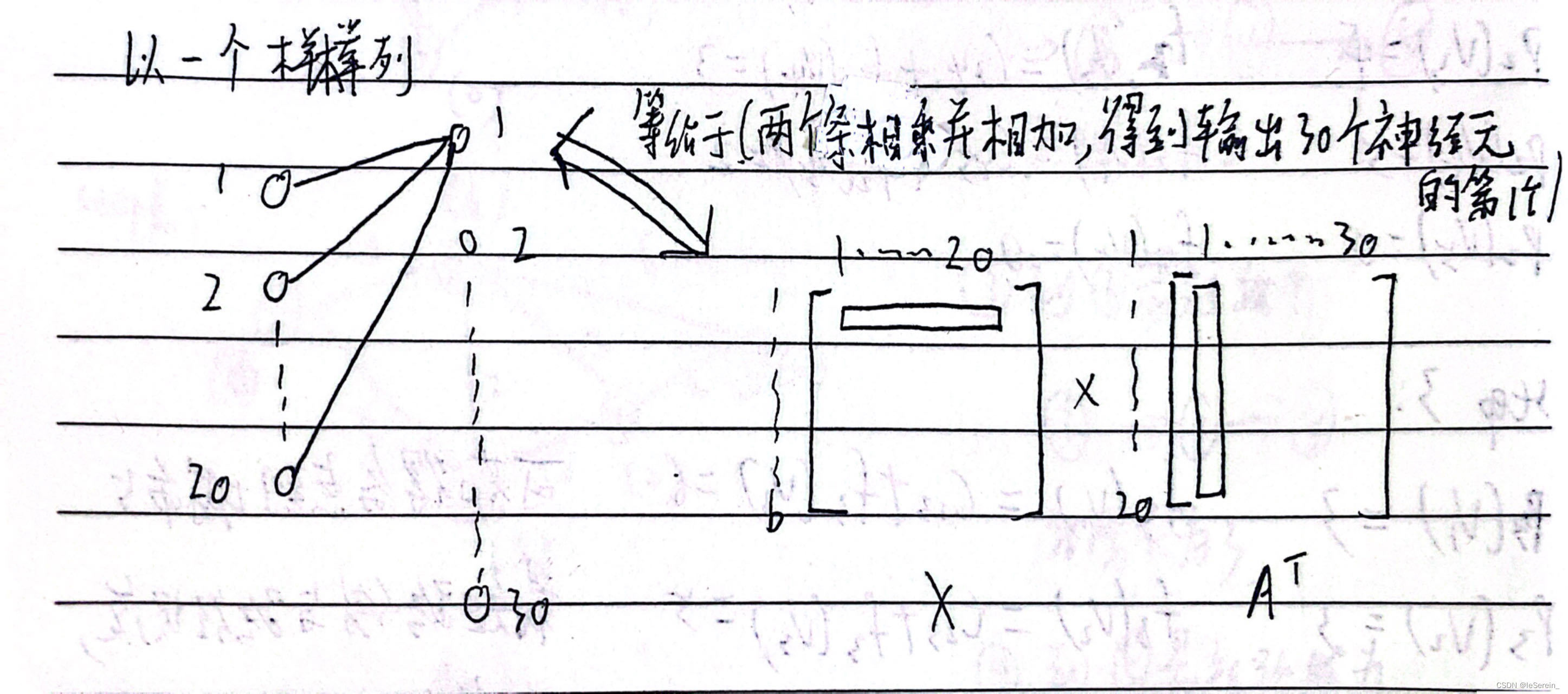
至此应该对代码的实现很理解了,但是需要注意,大家写文章中用的都还是Wx+b的写法。
不管怎样,文章和代码都是能对应上的,最多是表示方式的区别(有的用行向量,有的用列向量)
相关文章:

【pytorch】nn.linear 中为什么是y=xA^T+b
我记得读教材的时候是yWxb, 左乘矩阵W,这样才能表示线性变化。 但是pytorch中的nn.linear中,计算方式是yxA^Tb,其中A是权重矩阵。 为什么右乘也能表示线性变化操作呢?因为pytorch中,照顾到输入是多个样本一起算的&…...

vite打包原理
vite 工程化开发:打包工具 启动速度很快 核心原理还是webpack 把webpack封装了,把webpack对象封装了 和vue2整体结构几乎一致 webpack两种模式:开发&生产 代码打包编译,本地起一个web服务器实时预览编译后的结果 build 命令模…...
导出pdf 加密、加水印、加页脚
1.依赖 <dependency> <groupId>com.itextpdf</groupId> <artifactId>itextpdf</artifactId> <version>5.5.10</version> </dependency> <dependency> …...

Flutter 仿抖音 TikTok 上下滑动 播放视频
Flutter 仿抖音 TikTok 上下滑动 播放视频UI框架,视频播放使用 video_player github:GitHub - PangHaHa12138/TiktokVideo: Flutter 仿抖音 TikTok 上下滑动 播放视频UI框架 实现功能: 1.上下滑动自动播放切换视频,loading 封面…...

计算机网络——网络层(2)
计算机网络——网络层(2) 小程一言专栏链接: [link](http://t.csdnimg.cn/ZUTXU)前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家, [跳转到网站](https://www.captainbed.…...

01-16Maven-SpringBoot入门
Maven继承Maven高级SpringSpringBoot入门 Maven 一、概念及功能 概念:Maven是Apache软件基金会组织维护的一款专门为Java项目提供项目构建和依赖管理的工具 1.1作用: 项目构建 构建:是一个将代码从开发阶段到生产阶段的一个过程…...
微信小程序(二十七)列表渲染改变量名
注释很详细,直接上代码 上一篇 新增内容: 1.改变默认循环单元item变量名 2.改变默认循环下标index变量名 基础模板有问题可以先看上一篇 源码: index.wxml <view class"students"><view class"item"><te…...
k8s之安装部署及kuboard发布应用
目录 环境准备 系统规划 配置免密 将桥接的IPv4流量传递到iptables的链 系统基础配置 安装docker 安装docker及基础依赖 配置docker的仓库下载地址 部署k8s 添加阿里云的k8s源 安装kubeadm,kubelet和kubectl 初始化masteer节点 部署node节点 部署flanne…...
JProfiler for Mac:提升性能和诊断问题的终极工具
在当今的高性能计算和多线程应用中,性能优化和问题诊断是至关重要的。JProfiler for Mac 是一个强大的性能分析工具,旨在帮助开发者更好地理解其应用程序的运行情况,提升性能并快速诊断问题。 JProfiler for Mac 的主要特点包括:…...

力扣202-快乐数
快乐数 题目链接 解题思路: 两个指针,一快一慢,如果相遇,就会生成环如果环内元素为1,那么就可以返回 class Solution { public:int get(int n){int res 0;while(n){res (n%10) * (n%10);n / 10;}return res;}bool isHappy(int …...

牛客寒假训练营H题
思路:找出所有m的子集,加到价值中,找出最大价值即可。 代码: void solve(){int n, m;cin >> n >> m;vector<pii>a(n 1);for(int i 1;i < n;i )cin >> a[i].first >> a[i].second;int ans 0…...

ubuntu22.04@laptop 常用基础环境安装
ubuntu22.04laptop 常用基础环境安装 1. 源由2. 步骤2.1 安装ubuntu22.04 LTS系统2.2 必备软件安装2.3 基本远程环境2.3.1 远程ssh登录2.3.2 samba局域网2.3.3 VNC远程登录 2.4 开发环境安装 3. 总结 1. 源由 应朋友要求,整理下一个个人常用的工作笔记本常用开发环…...
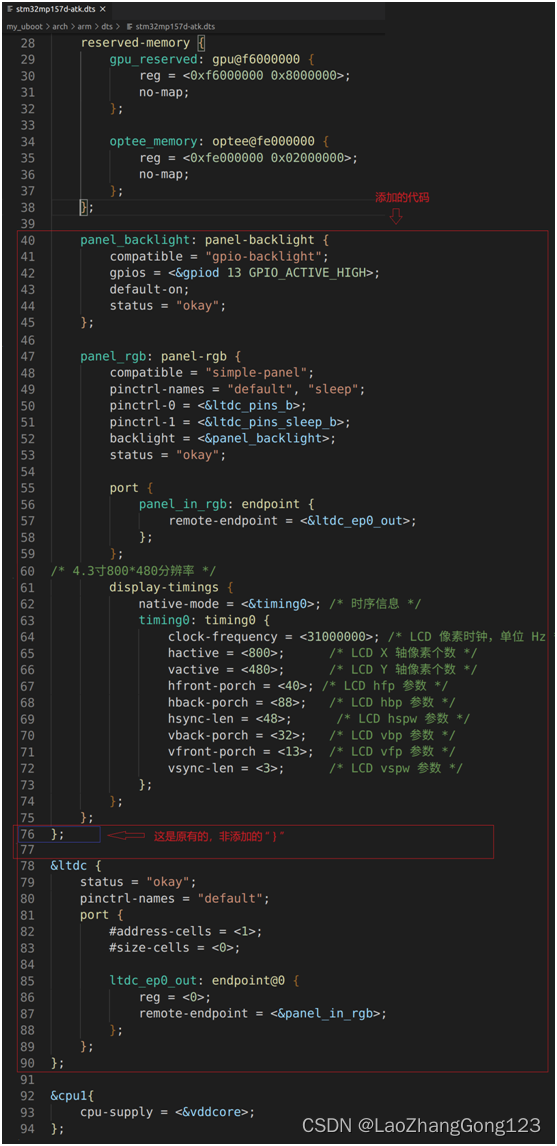
Linux第41步_移植ST公司uboot的第2步_修改网络驱动_USB OTG设备树_LCD驱动_以及编译和烧写测试
移植ST公司uboot的第1步,创建配置文件、设备树、修改电源管理和sdmmc节点后,还需要进一部修改,如:网络驱动、USB OTG设备树、LCD驱动,以及编译和烧写测试。 一、在虚拟机中,使用VSCode打开my_uboot工作区 …...
环境配置过程)
瑞芯微1808模型转换(onnx到rknn)环境配置过程
瑞芯微1808模型转换(onnx → \to →rknn)环境配置 阅读本解决方案前,请读者确保已经根据官方的相关教程【rknn_model_zoo/common/rknn_converter at v1.5.0 airockchip/rknn_model_zoo (github.com)】完成其他配置文件的修改,以…...
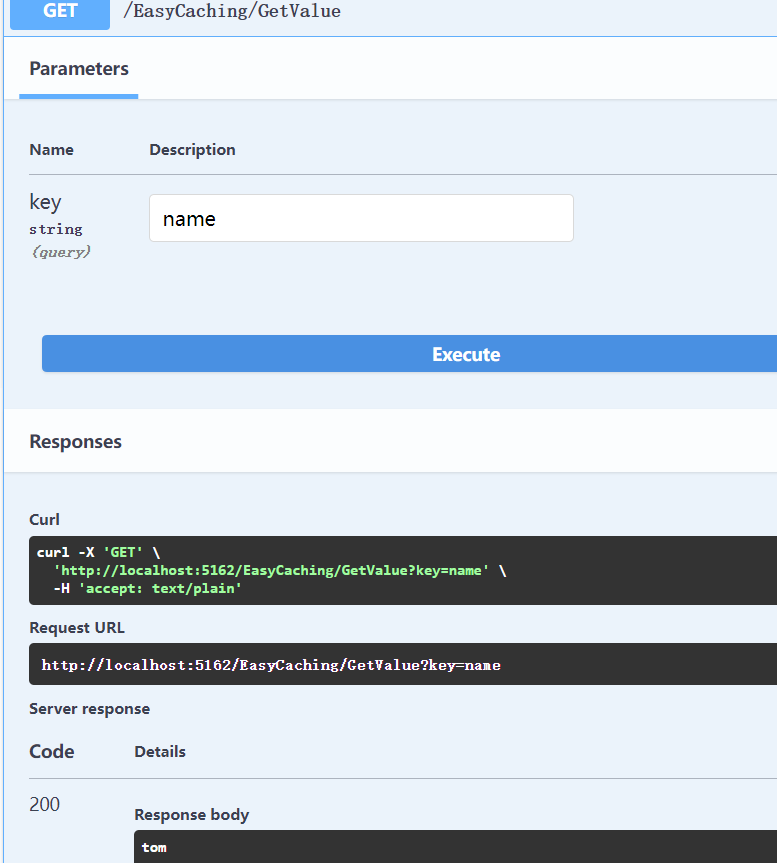
测试ASP.NET Core项目调用EasyCaching的基本用法(InMemory)
EasyCaching属于开源缓存库,支持基本缓存方式及高级缓存用法,提高用户操作缓存的效率。EasyCaching支持的缓存方式包括以下类型,本文学习最基础的InMemory方式的基本用法。 EasyCaching.InMemory包属于基于内存的缓存库,使用的…...
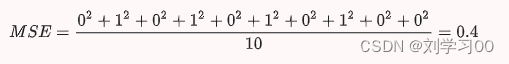
机器学习系列-2 线性回归训练损失
机器学习系列-2 线性回归&训练损失 学习内容来自:谷歌ai学习 https://developers.google.cn/machine-learning/crash-course/framing/check-your-understanding?hlzh-cn 本文作为学习记录1 线性回归: 举例:蝉(昆虫物种&…...

spring-boot-actuator 服务监控
1 概述 服务启动时,通过spring-boot-actuator 监控es等服务是否连接成功等 2 依赖 <!-- 服务监控 --> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-actuator</artifactId><…...
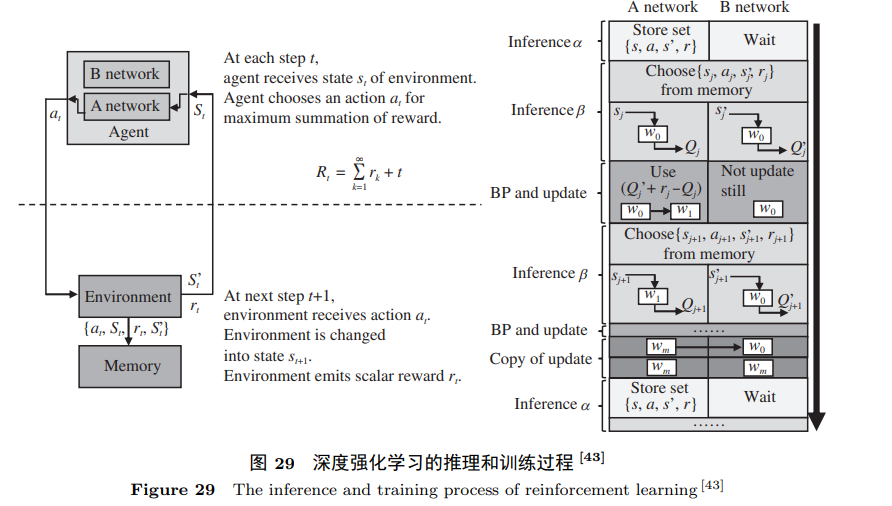
窥探向量乘矩阵的存内计算原理—基于向量乘矩阵的存内计算
在当今计算领域中,存内计算技术凭借其出色的向量乘矩阵操作效能引起了广泛关注。本文将深入研究基于向量乘矩阵的存内计算原理,并探讨几个引人注目的代表性工作,如DPE、ISAAC、PRIME等,它们在神经网络和图计算应用中表现出色&…...
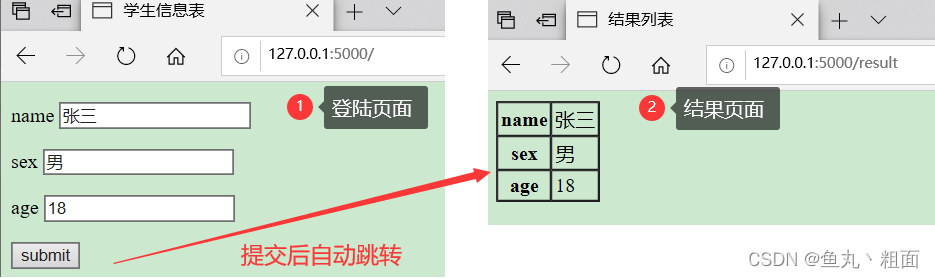
Python flask 表单详解
文章目录 1 概述1.1 request 对象 2 示例2.1 目录结构2.2 student.html2.3 result.html2.4 app.py 1 概述 1.1 request 对象 作用:来自客户端网页的数据作为全局请求对象发送到服务器request 对象的重要属性如下: 属性解释form字典对象,包…...
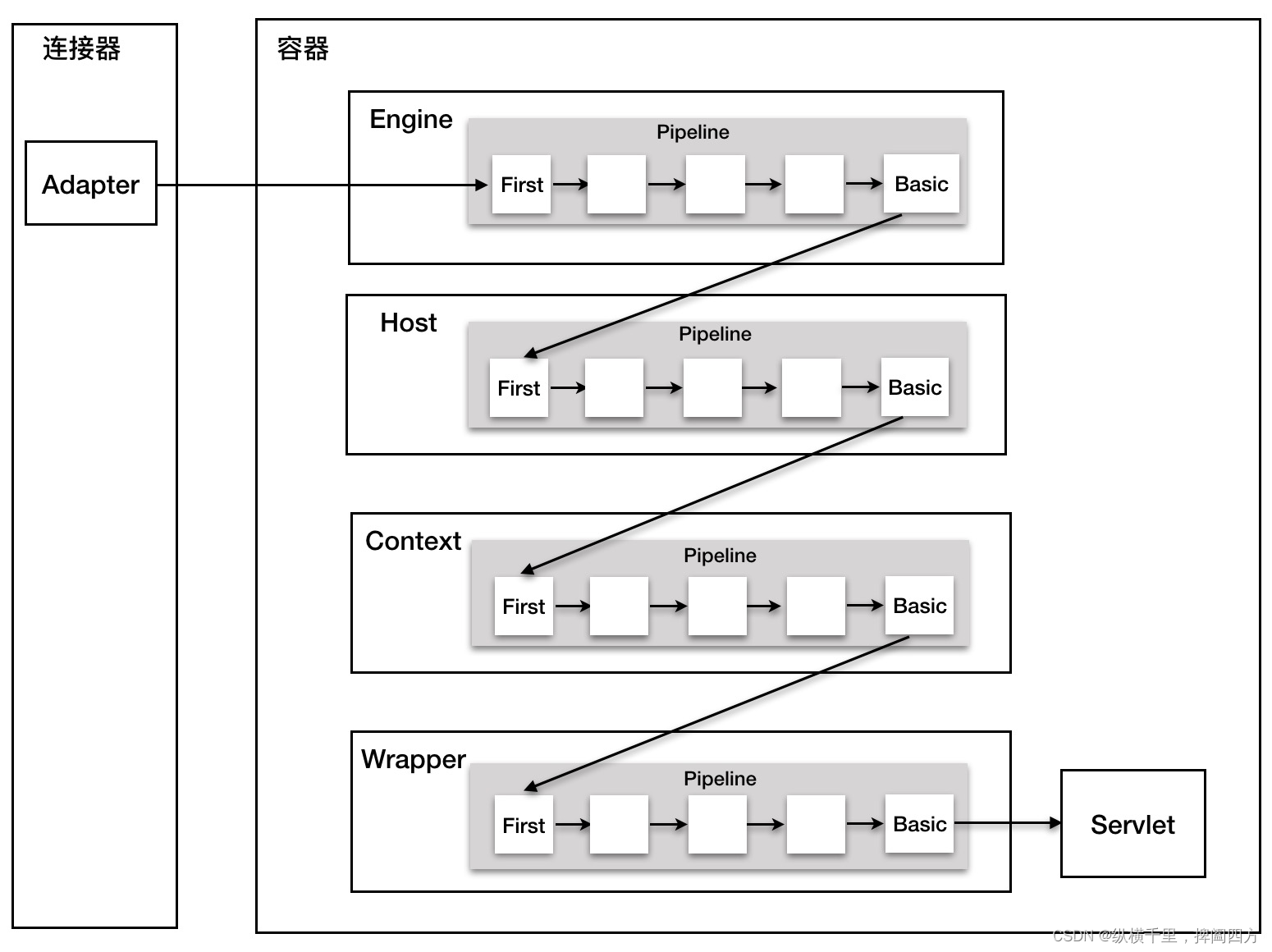
【Tomcat与网络3】Tomcat的整体架构
目录 1.演进1:将连接和处理服务分开 2演进2:Container的演进 3 再论Tomcat的容器结构 4 Tomcat处理请求的过程 5 请求的处理过程与Pipeline-Valve管道 在前面我们介绍了Servlet的基本原理,本文我们结合Tomcat来分析一下如何设计一个大型…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...
