当前位置： 首页 > news >正文

PHP之PDO_MYSQL扩展安装步骤

news 2026/2/9 14:58:02

1，如果有php源码包可以不用下载，在 源码包下的 ext/ 下面可以找到

cd php-8.1.9/ext/pdo_mysql

2,如果存在，直接安装

/usr/local/php-8.1.9/bin/phpize
./configure --with-php-config=/usr/local/php-8.1.9/bin/php-config
make && sudo make install

3，然后去php.ini文件里面添加extension即可

附录：

make报错：使用 -std=c99 或 -std=gnu99 来编译您的代码
make CFLAGS=-std=c99 或make CFLAGS=-std=gnu99 
编译安装PHP时报错configure: error: Cannot find MySQL header files under

yum -y install mysql-devel 即可解决！

相关文章：

PHP之PDO_MYSQL扩展安装步骤

1，如果有php源码包可以不用下载，在 源码包下的 ext/ 下面可以找到 cd php-8.1.9/ext/pdo_mysql 2,如果存在，直接安装 /usr/local/php-8.1.9/bin/phpize ./configure --with-php-config/usr/local/php-8.1.9/bin/php-config make &&a…...

编程日记 2024/2/4 2:22:09

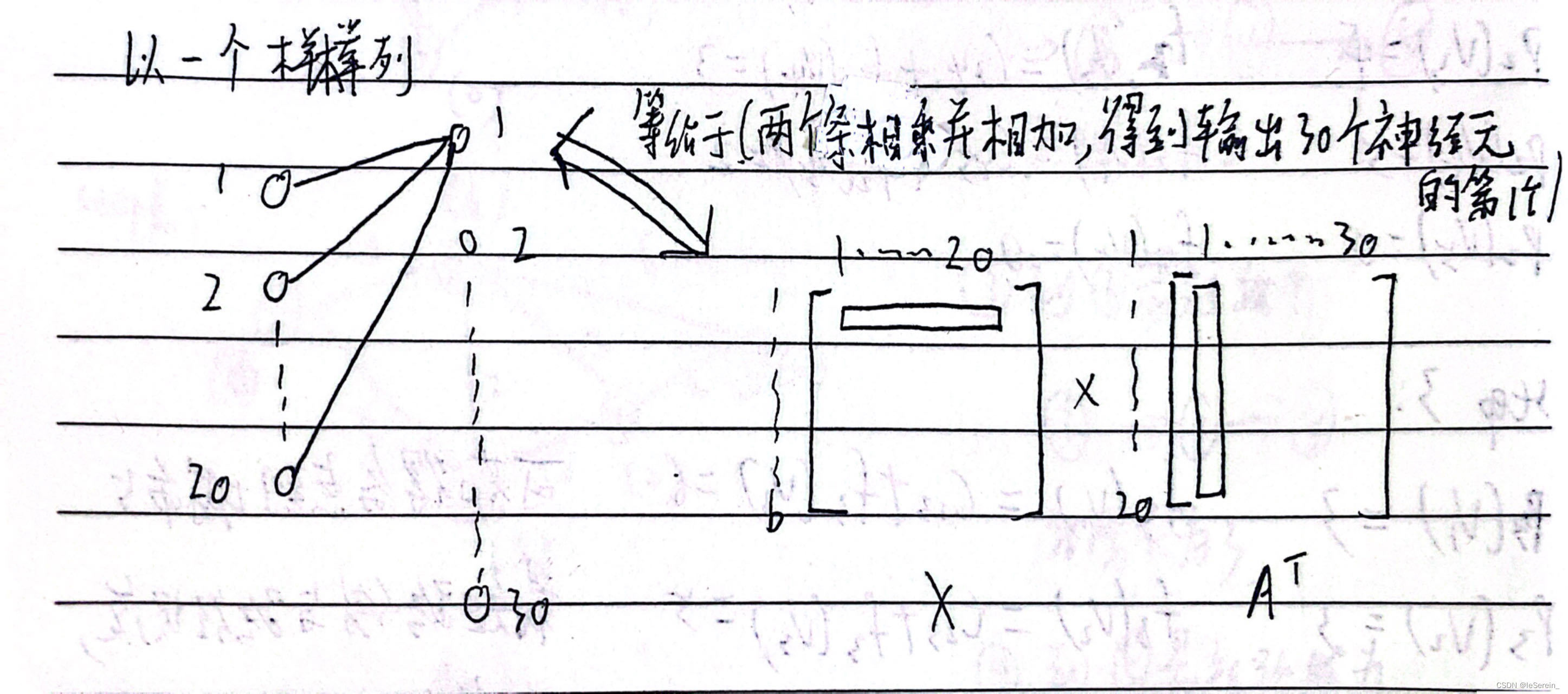
【pytorch】nn.linear 中为什么是y=xA^T+b

我记得读教材的时候是yWxb, 左乘矩阵W，这样才能表示线性变化。 但是pytorch中的nn.linear中，计算方式是yxA^Tb，其中A是权重矩阵。 为什么右乘也能表示线性变化操作呢？因为pytorch中，照顾到输入是多个样本一起算的&…...

编程日记 2024/2/4 2:21:07

vite打包原理

vite 工程化开发：打包工具 启动速度很快 核心原理还是webpack 把webpack封装了，把webpack对象封装了 和vue2整体结构几乎一致 webpack两种模式：开发&生产 代码打包编译，本地起一个web服务器实时预览编译后的结果 build 命令模…...

编程日记 2024/2/4 2:18:05

导出pdf 加密、加水印、加页脚

1.依赖 <dependency> <groupId>com.itextpdf</groupId> <artifactId>itextpdf</artifactId> <version>5.5.10</version> </dependency> <dependency> …...

编程日记 2024/2/4 2:11:59

Flutter 仿抖音 TikTok 上下滑动 播放视频

Flutter 仿抖音 TikTok 上下滑动 播放视频UI框架&#xff0c;视频播放使用 video_player github&#xff1a;GitHub - PangHaHa12138/TiktokVideo: Flutter 仿抖音 TikTok 上下滑动 播放视频UI框架 实现功能&#xff1a; 1.上下滑动自动播放切换视频&#xff0c;loading 封面…...

编程日记 2024/2/4 2:09:57

计算机网络——网络层（2）

计算机网络——网络层&#xff08;2&#xff09; 小程一言专栏链接: [link](http://t.csdnimg.cn/ZUTXU)前些天发现了一个巨牛的人工智能学习网站&#xff0c;通俗易懂&#xff0c;风趣幽默&#xff0c;忍不住分享一下给大家&#xff0c; [跳转到网站](https://www.captainbed.…...

编程日记 2024/2/4 2:08:56

01-16Maven-SpringBoot入门

Maven继承Maven高级SpringSpringBoot入门 Maven 一、概念及功能 概念&#xff1a;Maven是Apache软件基金会组织维护的一款专门为Java项目提供项目构建和依赖管理的工具 1.1作用&#xff1a; 项目构建 构建&#xff1a;是一个将代码从开发阶段到生产阶段的一个过程&#xf…...

编程日记 2024/2/4 2:04:52

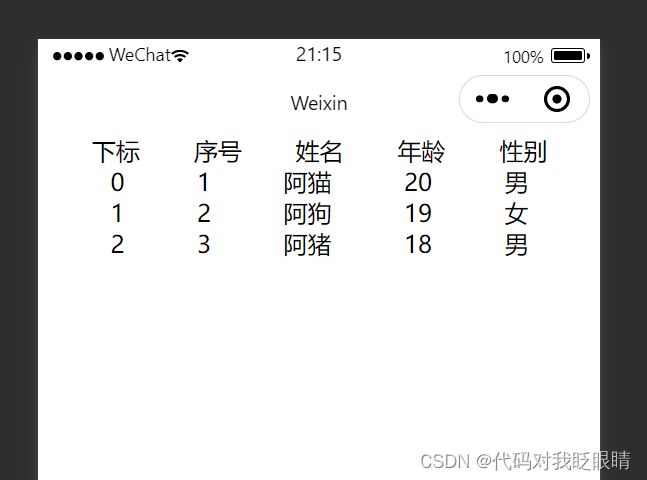
微信小程序（二十七）列表渲染改变量名

注释很详细&#xff0c;直接上代码 上一篇 新增内容&#xff1a; 1.改变默认循环单元item变量名 2.改变默认循环下标index变量名 基础模板有问题可以先看上一篇 源码&#xff1a; index.wxml <view class"students"><view class"item"><te…...

编程日记 2024/2/4 2:03:51

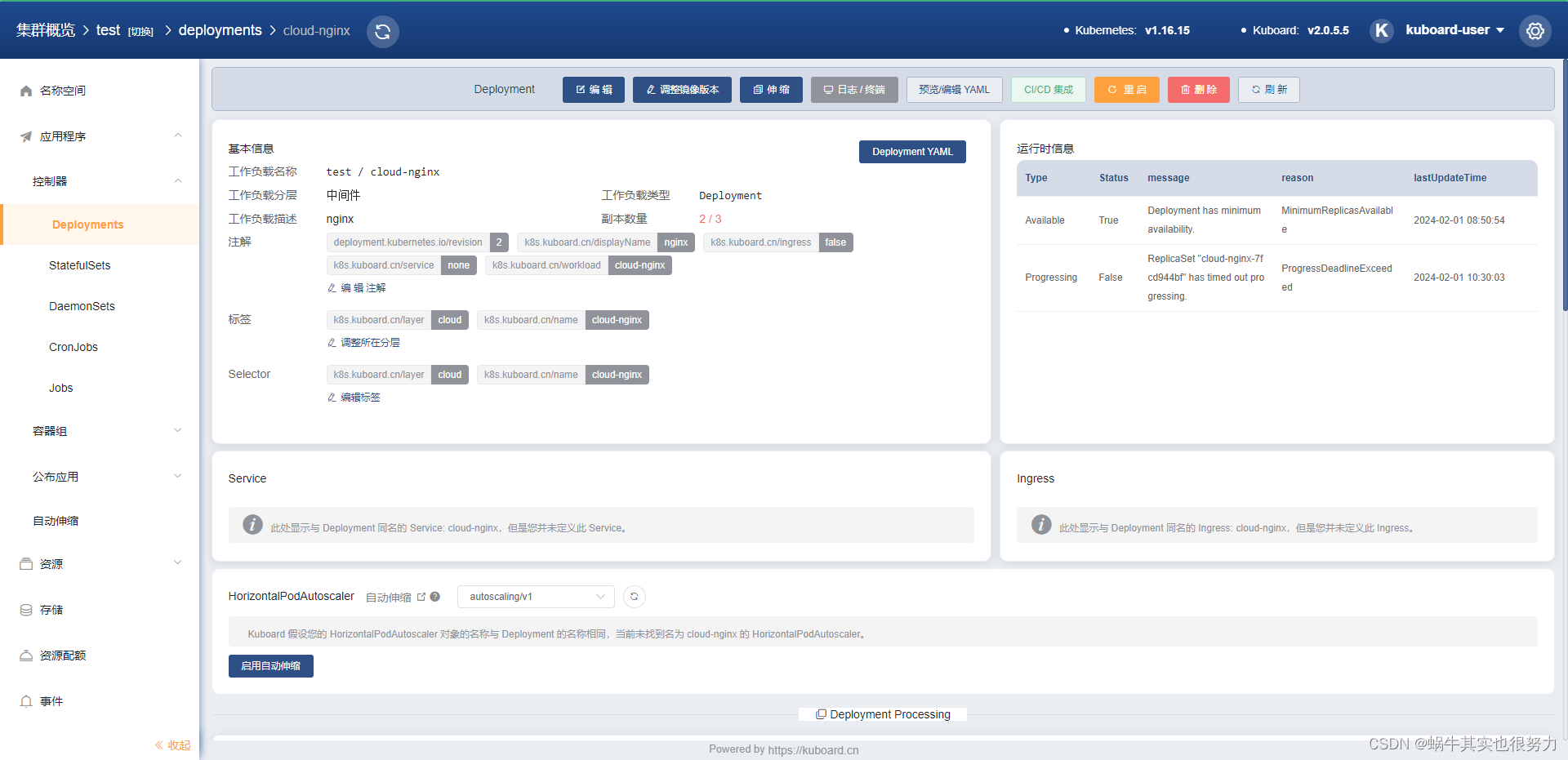
k8s之安装部署及kuboard发布应用

目录 环境准备 系统规划 配置免密 将桥接的IPv4流量传递到iptables的链 系统基础配置 安装docker 安装docker及基础依赖 配置docker的仓库下载地址 部署k8s 添加阿里云的k8s源 安装kubeadm&#xff0c;kubelet和kubectl 初始化masteer节点 部署node节点 部署flanne…...

编程日记 2024/2/4 2:00:48

JProfiler for Mac：提升性能和诊断问题的终极工具

在当今的高性能计算和多线程应用中&#xff0c;性能优化和问题诊断是至关重要的。JProfiler for Mac 是一个强大的性能分析工具&#xff0c;旨在帮助开发者更好地理解其应用程序的运行情况&#xff0c;提升性能并快速诊断问题。 JProfiler for Mac 的主要特点包括&#xff1a;…...

编程日记 2024/2/4 1:59:46

力扣202-快乐数

快乐数 题目链接 解题思路&#xff1a; 两个指针&#xff0c;一快一慢&#xff0c;如果相遇&#xff0c;就会生成环如果环内元素为1,那么就可以返回 class Solution { public:int get(int n){int res 0;while(n){res (n%10) * (n%10);n / 10;}return res;}bool isHappy(int …...

编程日记 2024/2/4 1:57:44

牛客寒假训练营H题

思路&#xff1a;找出所有m的子集&#xff0c;加到价值中&#xff0c;找出最大价值即可。 代码&#xff1a; void solve(){int n, m;cin >> n >> m;vector<pii>a(n 1);for(int i 1;i < n;i )cin >> a[i].first >> a[i].second;int ans 0…...

编程日记 2024/2/4 1:55:43

ubuntu22.04@laptop 常用基础环境安装

ubuntu22.04laptop 常用基础环境安装 1. 源由2. 步骤2.1 安装ubuntu22.04 LTS系统2.2 必备软件安装2.3 基本远程环境2.3.1 远程ssh登录2.3.2 samba局域网2.3.3 VNC远程登录 2.4 开发环境安装 3. 总结 1. 源由 应朋友要求&#xff0c;整理下一个个人常用的工作笔记本常用开发环…...

编程日记 2024/2/4 1:54:42

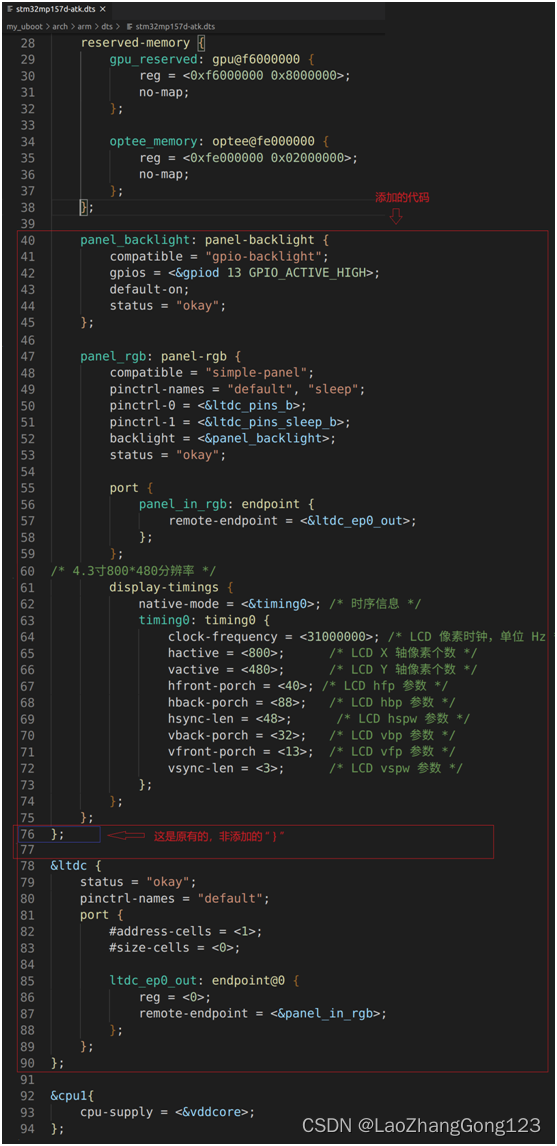
Linux第41步_移植ST公司uboot的第2步_修改网络驱动_USB OTG设备树_LCD驱动_以及编译和烧写测试

移植ST公司uboot的第1步&#xff0c;创建配置文件、设备树、修改电源管理和sdmmc节点后&#xff0c;还需要进一部修改&#xff0c;如&#xff1a;网络驱动、USB OTG设备树、LCD驱动&#xff0c;以及编译和烧写测试。 一、在虚拟机中&#xff0c;使用VSCode打开my_uboot工作区 …...

编程日记 2024/2/4 1:52:39

瑞芯微1808模型转换(onnx到rknn)环境配置过程

瑞芯微1808模型转换&#xff08;onnx → \to →rknn&#xff09;环境配置 阅读本解决方案前&#xff0c;请读者确保已经根据官方的相关教程【rknn_model_zoo/common/rknn_converter at v1.5.0 airockchip/rknn_model_zoo (github.com)】完成其他配置文件的修改&#xff0c;以…...

编程日记 2024/2/4 1:50:37

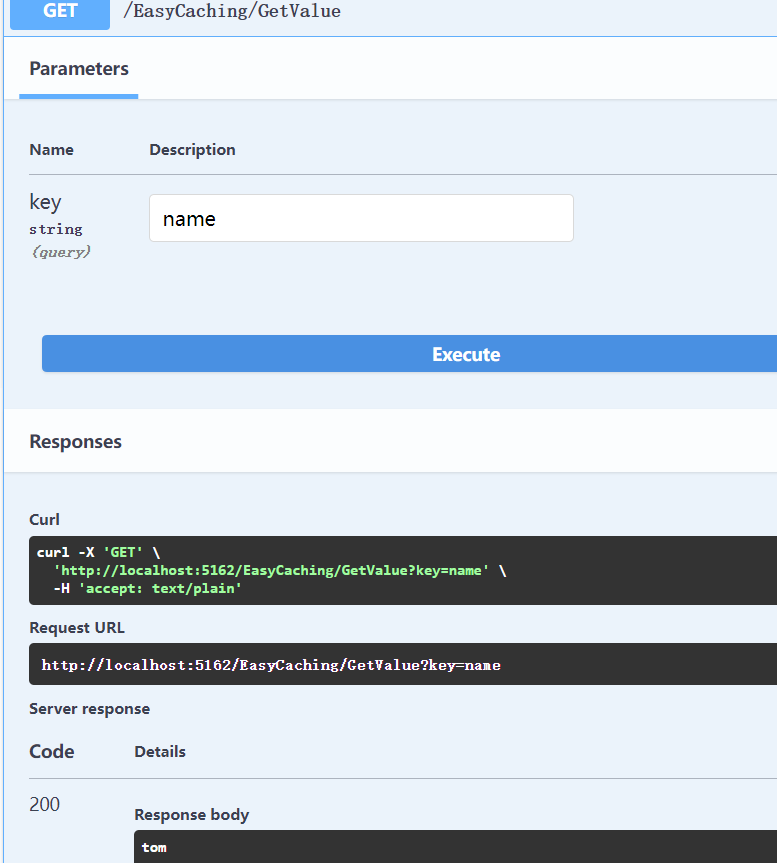
测试ASP.NET Core项目调用EasyCaching的基本用法（InMemory）

EasyCaching属于开源缓存库&#xff0c;支持基本缓存方式及高级缓存用法&#xff0c;提高用户操作缓存的效率。EasyCaching支持的缓存方式包括以下类型&#xff0c;本文学习最基础的InMemory方式的基本用法。   EasyCaching.InMemory包属于基于内存的缓存库&#xff0c;使用的…...

编程日记 2024/2/4 1:49:35

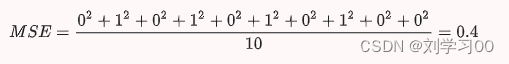
机器学习系列-2 线性回归训练损失

机器学习系列-2 线性回归&训练损失 学习内容来自&#xff1a;谷歌ai学习 https://developers.google.cn/machine-learning/crash-course/framing/check-your-understanding?hlzh-cn 本文作为学习记录1 线性回归&#xff1a; 举例&#xff1a;蝉&#xff08;昆虫物种&…...

编程日记 2024/2/4 1:44:29

spring-boot-actuator 服务监控

1 概述 服务启动时&#xff0c;通过spring-boot-actuator 监控es等服务是否连接成功等 2 依赖 <!-- 服务监控 --> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-actuator</artifactId><…...

编程日记 2024/2/4 1:43:28

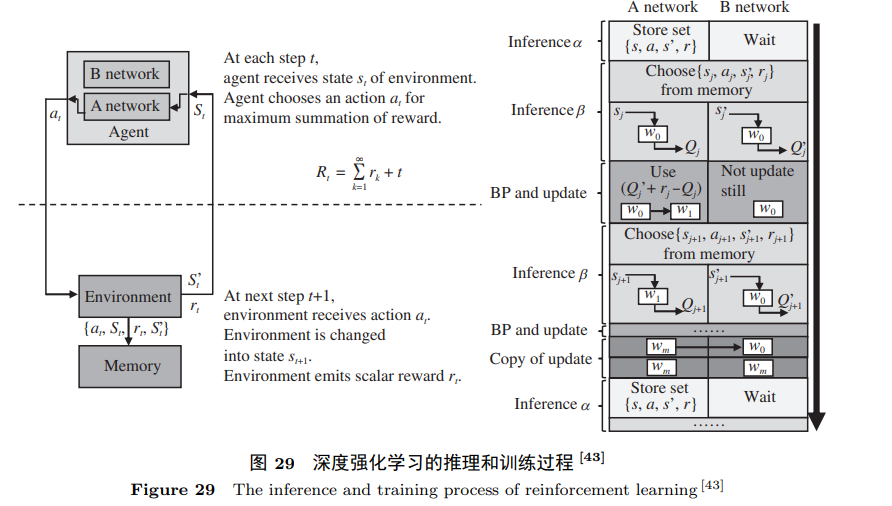
窥探向量乘矩阵的存内计算原理—基于向量乘矩阵的存内计算

在当今计算领域中&#xff0c;存内计算技术凭借其出色的向量乘矩阵操作效能引起了广泛关注。本文将深入研究基于向量乘矩阵的存内计算原理&#xff0c;并探讨几个引人注目的代表性工作&#xff0c;如DPE、ISAAC、PRIME等&#xff0c;它们在神经网络和图计算应用中表现出色&…...

编程日记 2024/2/4 1:42:27

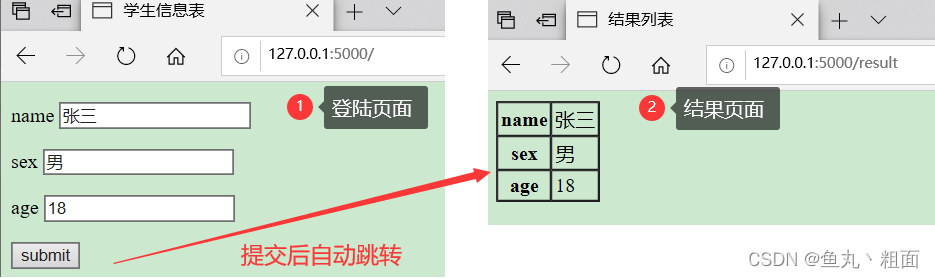
Python flask 表单详解

文章目录 1 概述1.1 request 对象 2 示例2.1 目录结构2.2 student.html2.3 result.html2.4 app.py 1 概述 1.1 request 对象 作用&#xff1a;来自客户端网页的数据作为全局请求对象发送到服务器request 对象的重要属性如下&#xff1a; 属性解释form字典对象&#xff0c;包…...

编程日记 2024/2/4 1:40:25

Unity3D中Gfx.WaitForPresent优化方案

前言 在Unity中&#xff0c;Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染&#xff08;即CPU被阻塞&#xff09;&#xff0c;这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案&#xff1a; 对惹&#xff0c;这里有一个游戏开发交流小组&…...

编程新知 2026/2/7 17:31:44

【大模型RAG】Docker 一键部署 Milvus 完整攻略

本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装&#xff1b;只需暴露 19530&#xff08;gRPC&#xff09;与 9091&#xff08;HTTP/WebUI&#xff09;两个端口&#xff0c;即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

编程新知 2026/1/31 8:08:07

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?

论文网址&#xff1a;pdf 英文是纯手打的&#xff01;论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误&#xff0c;若有发现欢迎评论指正&#xff01;文章偏向于笔记&#xff0c;谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

编程新知 2026/2/6 14:42:11

剑指offer20_链表中环的入口节点

链表中环的入口节点 给定一个链表&#xff0c;若其中包含环&#xff0c;则输出环的入口节点。 若其中不包含环&#xff0c;则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

编程新知 2026/1/31 6:09:22

三体问题详解

从物理学角度&#xff0c;三体问题之所以不稳定&#xff0c;是因为三个天体在万有引力作用下相互作用&#xff0c;形成一个非线性耦合系统。我们可以从牛顿经典力学出发&#xff0c;列出具体的运动方程&#xff0c;并说明为何这个系统本质上是混沌的&#xff0c;无法得到一般解…...

编程新知 2025/10/19 5:14:05

Android第十三次面试总结（四大 组件基础）

Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成&#xff0c;用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机&#xff1a; ​onCreate()​​ ​调用时机​&#xff1a;Activity 首次创建时调用。​…...

编程新知 2025/10/15 15:07:34

React---day11

14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store&#xff1a; 我们在使用异步的时候理应是要使用中间件的&#xff0c;但是configureStore 已经自动集成了 redux-thunk&#xff0c;注意action里面要返回函数 import { configureS…...

编程新知 2026/1/19 2:13:24

JAVA后端开发——多租户

数据隔离是多租户系统中的核心概念&#xff0c;确保一个租户&#xff08;在这个系统中可能是一个公司或一个独立的客户&#xff09;的数据对其他租户是不可见的。在 RuoYi 框架&#xff08;您当前项目所使用的基础框架&#xff09;中&#xff0c;这通常是通过在数据表中增加一个…...

编程新知 2025/12/18 8:35:12

Webpack性能优化：构建速度与体积优化策略

一、构建速度优化 1、​​升级Webpack和Node.js​​ ​​优化效果​​&#xff1a;Webpack 4比Webpack 3构建时间降低60%-98%。​​原因​​&#xff1a; V8引擎优化&#xff08;for of替代forEach、Map/Set替代Object&#xff09;。默认使用更快的md4哈希算法。AST直接从Loa…...

编程新知 2025/12/26 15:05:09

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表

设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程，两张表是相同的结构，都有整型主键id字段，需要每次从数据库分批取得2000条数据，用于比较，比较操作的同时可以再取2000条数据，等上一次比较完成之后，开始比较，直到比较完所有的数据。比较操作需要比较…...

编程新知 2025/9/14 5:35:46