「优选算法刷题」:计算布尔二叉树的值
一、题目
给你一棵 完整二叉树 的根,这棵树有以下特征:
- 叶子节点 要么值为
0要么值为1,其中0表示False,1表示True。 - 非叶子节点 要么值为
2要么值为3,其中2表示逻辑或OR,3表示逻辑与AND。
计算 一个节点的值方式如下:
- 如果节点是个叶子节点,那么节点的 值 为它本身,即
True或者False。 - 否则,计算 两个孩子的节点值,然后将该节点的运算符对两个孩子值进行 运算 。
返回根节点 root 的布尔运算值。
完整二叉树 是每个节点有 0 个或者 2 个孩子的二叉树。
叶子节点 是没有孩子的节点。
示例 1:
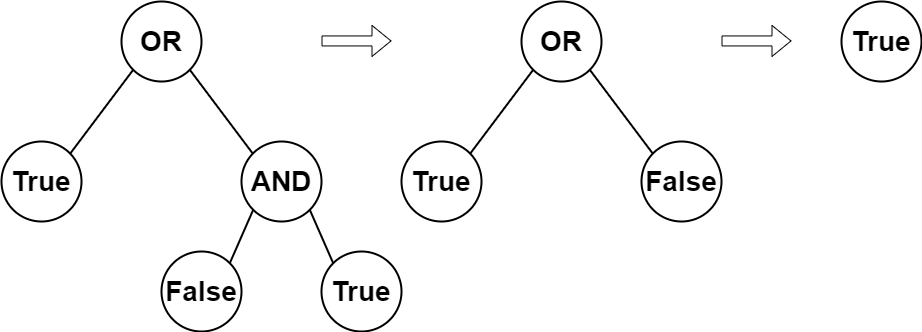
输入:root = [2,1,3,null,null,0,1] 输出:true 解释:上图展示了计算过程。 AND 与运算节点的值为 False AND True = False 。 OR 运算节点的值为 True OR False = True 。 根节点的值为 True ,所以我们返回 true 。
示例 2:
输入:root = [0] 输出:false 解释:根节点是叶子节点,且值为 false,所以我们返回 false 。
提示:
- 树中节点数目在
[1, 1000]之间。 0 <= Node.val <= 3- 每个节点的孩子数为
0或2。 - 叶子节点的值为
0或1。 - 非叶子节点的值为
2或3
二、思路解析
二叉树,大部分都是用到递归来实现的,所以,这道题我们可以有意地往递归上靠。
而递归一大重点就是,我们要寻找 每次递归中的相同子问题。
也就是计算所有子节点的值,而这则是通过子节点的值运算出的。
抽象一下递归函数流程就是:
1. 当前问题规模为 n=1 时,即叶子节点,直接返回当前节点值;
2. 递归求得左右子节点的值;
3. 通过判断当前节点的逻辑运算符,计算左右子节点值运算得出的结果;
具体运算结合题目的条件即可,下面是完整代码实现👇
三、完整代码
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean evaluateTree(TreeNode root) {if(root.left == null){return root.val == 0 ? false : true; }boolean left = evaluateTree(root.left);boolean right = evaluateTree(root.right);return root.val == 2 ? left | right : left & right;}
}以上就是本篇博客的全部内容啦,如有不足之处,还请各位指出,期待能和各位一起进步!
相关文章:

「优选算法刷题」:计算布尔二叉树的值
一、题目 给你一棵 完整二叉树 的根,这棵树有以下特征: 叶子节点 要么值为 0 要么值为 1 ,其中 0 表示 False ,1 表示 True 。非叶子节点 要么值为 2 要么值为 3 ,其中 2 表示逻辑或 OR ,3 表示逻辑与 AND…...

A系统数据表同步到B系统数据表
一、 事务操作 (小量数据) 事务操作通常用于确保数据的一致性和完整性。以下是一些常见的应用场景: 银行转账:当从一个账户向另一个账户转账时,需要确保两个操作(从一个账户扣款和向另一个账户存款&#x…...
Qt实现类似ToDesk顶层窗口 不规则按钮
先看效果: 在进行多进程开发时,可能会遇到需要进行全局弹窗的需求。 因为平时会使用ToDesk进行远程桌面控制,在电脑被控时,ToDesk会在右下角进行一个顶层窗口的提示,效果如下: 其实要实现顶层窗口…...
发布4-运行JRT程序
到了本章节,你需要准备好JDK17的环境和idea环境。并且安装好选择的数据库软件。这章将正式开始JRT的程序开发。 首先获取程序,我会给下载地址 下载后解压会得到下图目录的文件结构,DBFile放IRIS和PG的数据库文件,JRTClient放打包…...
利用VPN设备漏洞入侵!新型勒索软件CACTUS攻击手法分析
近期,亚信安全应急响应中心截获了利用VPN设备已知漏洞传播的新型勒索软件CACTUS,该勒索于2023年3月首次被发现,一直保持着活跃状态。CACTUS勒索软件通过Fortinet VPN的已知漏洞进行入侵(黑客首先获取到VPN账号,再通过V…...

第7章 SpringBoot安全管理
学习目标 了解SpringSecurity安全管理的功能 掌握SpringSecurity的安全配置 掌握SpringSecurity自定义用户认证的实现方法 掌握SpringSecurity自定义用户授权管理的实现方法 掌握如何使用SpringSecurity实现页面控制 实际开发中,一些应用通常要考虑到安全性问题。例如,对于一…...
【QT+QGIS跨平台编译】之二十二:【FontConfig+Qt跨平台编译】(一套代码、一套框架,跨平台编译)
文章目录 一、FontConfig介绍二、文件下载三、文件分析四、pro文件五、编译实践 一、FontConfig介绍 FontConfig 是一个用于配置和定制字体的库,广泛应用于基于X Window系统的操作系统中,尤其是在Linux和Unix-like系统中。它为应用程序提供了一种统一的…...
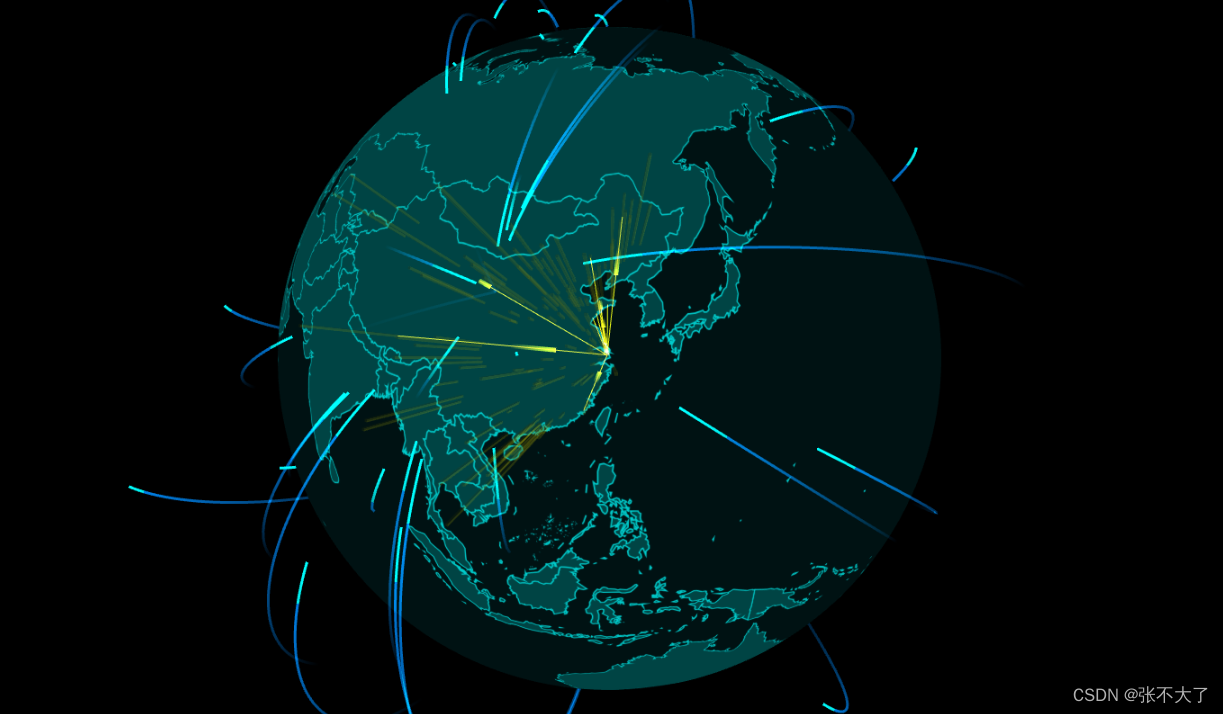
echarts中绘制3D三维地球
简介 echarts中的三维地球,需要用到世界地图json数据,我把json文件放到我的资源中,有需要的自行下载。 安装插件 // 安装echats npm install echarts --save npm install echarts-gl --save 项目中引用 1,引入安装的echarts…...
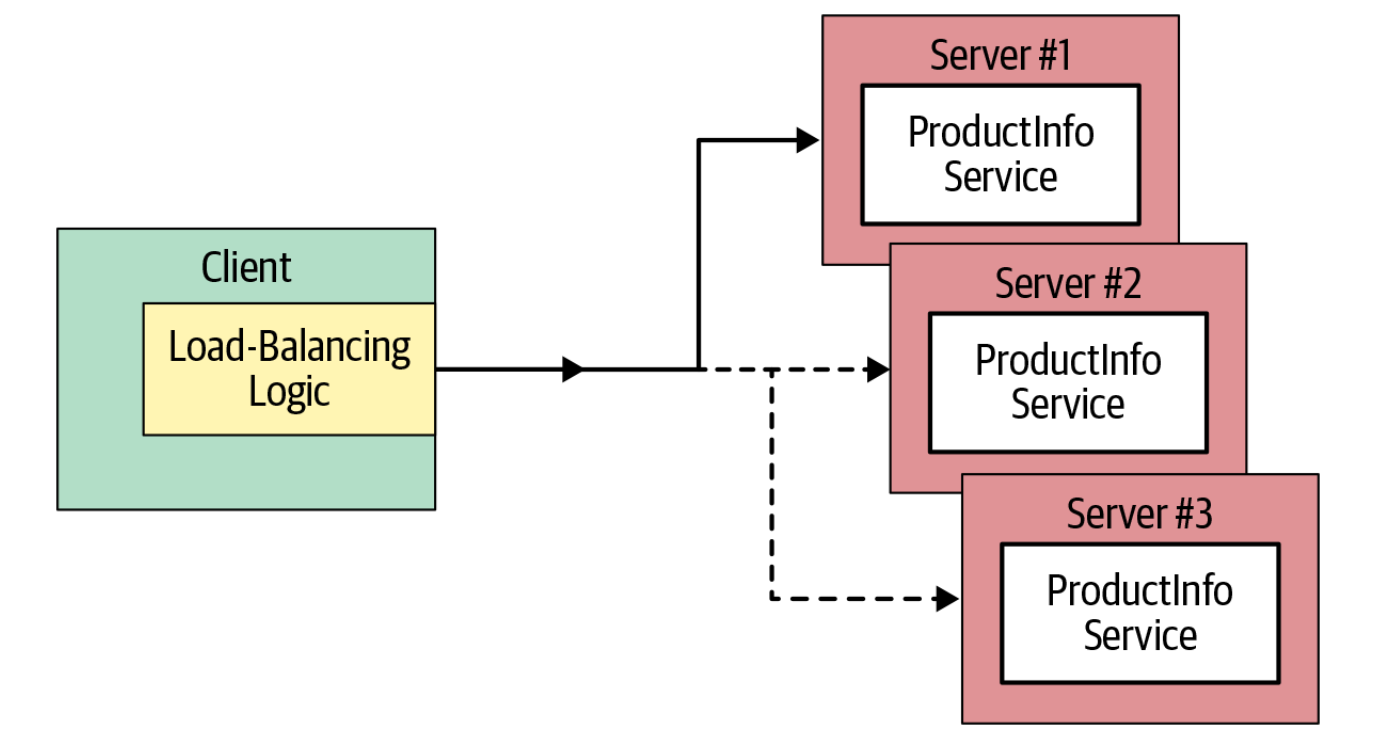
go grpc高级用法
文章目录 错误处理常规用法进阶用法原理 多路复用元数据负载均衡压缩数据 错误处理 gRPC 一般不在 message 中定义错误。毕竟每个 gRPC 服务本身就带一个 error 的返回值,这是用来传输错误的专用通道。gRPC 中所有的错误返回都应该是 nil 或者 由 status.Status 产…...

Redis实现登录的优化
目录 1 前言 2 实现步骤 2.1 软件环境准备 2.1.1 Redis的安装 2.1.2 在pom.xml中添加依赖 2.1.3 在application.yml中进行相关配置 2.2 StringRedisTemplate的常用方法 2.2.1 获取operations 2.2.2 主要方法 2.3 令牌主动失效机制 2.3.1 登录时将令牌存入Redis 2.…...
ROS方向第二次汇报(5)
文章目录 1.本方向内学习内容:1.1.自定义msg:1.1.1.定义msg文件:1.1.2.编辑配置文件: 1.2.自定义srv:1.2.1.定义srv文件:1.2.2.编辑配置文件: 1.3.服务通信案例实现:1.3.1.服务端实现…...

C# 浅克隆与深克隆
在C#中,浅克隆(Shallow Clone)和深克隆(Deep Clone)是两种常见的对象克隆技术,用于创建对象的新副本。 它们的主要区别在于复制对象的层次和属性的处理方式。 浅克隆(Shallow Copy)…...

Shell 正则表达式及综合案例及文本处理工具
目录 一、常规匹配 二、常用特殊字符 三、匹配手机号 四、案例之归档文件 五、案例之定时归档文件 六、Shell文本处理工具 1. cut工具 2. awk工具 一、常规匹配 一串不包含特殊字符的正则表达式匹配它自己 例子,比如说想要查看密码包含root字符串的&#x…...
React | Center 组件
在 Flutter 中有 Center 组件,效果就是让子组件整体居中,挺好用。 React 中虽然没有对应的组件,但是可以简单封装一个: index.less .container {display: flex;justify-content: center;align-items: center;align-content: ce…...

头歌C++之函数强化练习题
目录 第1关:结构实现复数运算 任务描述 编程要求 第2关:求亲密对数 任务描述 编程要求 第3关:计算一年的第几天 任务描述 编程要求 第4关:正整数求和 任务描述 编程要求 第5关:Pig Latin 任务描述 编程要求 第6关:打印日历 任务描述 编程要求 第1关:结…...
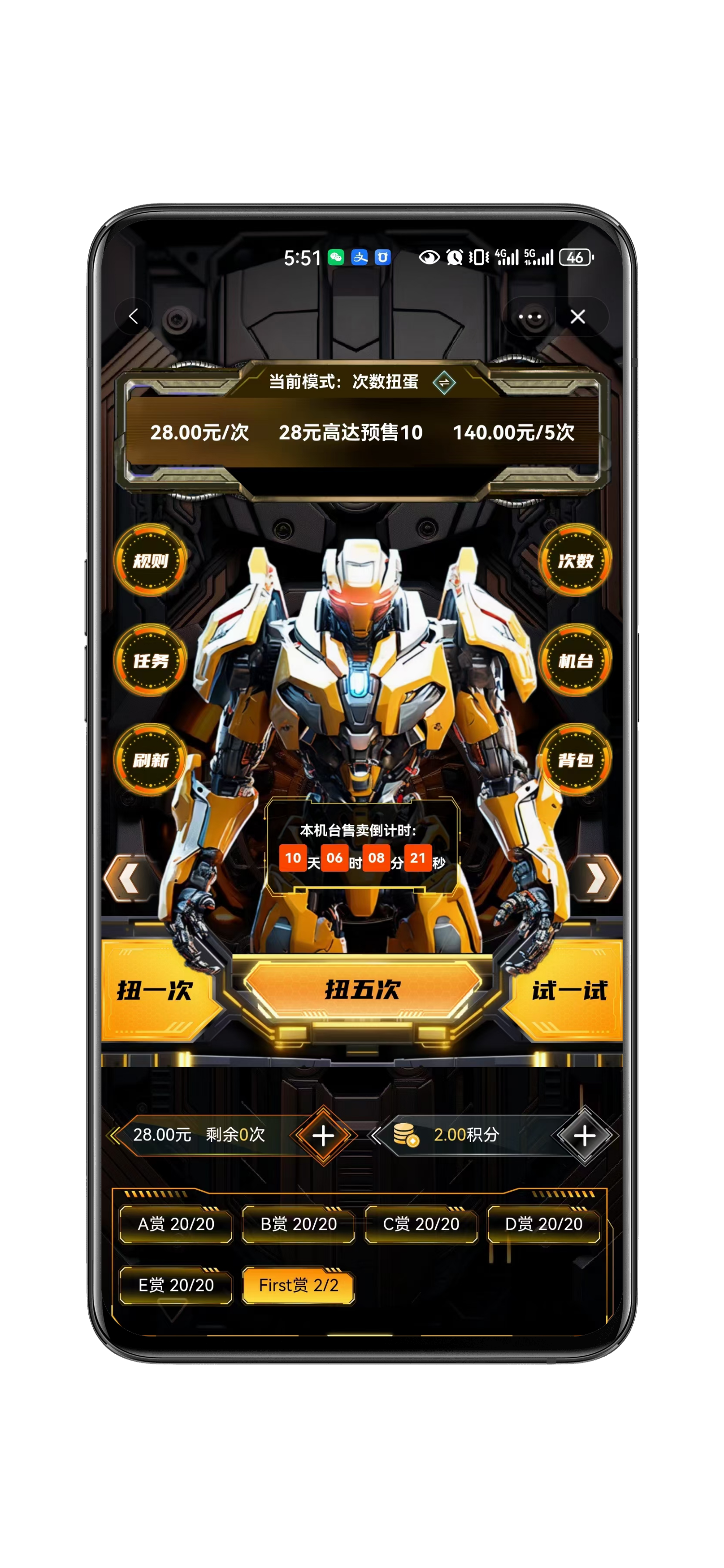
淘宝扭蛋机小程序:开启你的惊喜之旅
随着移动互联网的飞速发展,各种小程序层出不穷,其中,淘宝扭蛋机小程序以其独特的互动性和趣味性,吸引了大量用户。本文将为你详细介绍这款小程序的特色功能、用户体验以及如何使用,助你开启一段惊喜之旅。 一、特色功…...
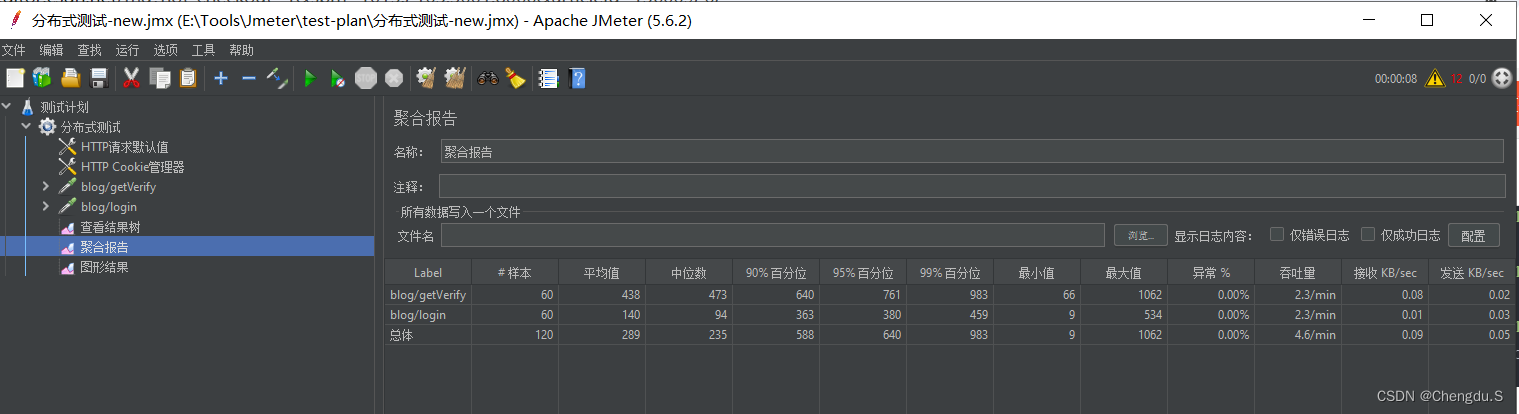
Jmeter 基于Docker 实现分布式测试
基于Docker 实现分布式测试 制作Jmeter基础镜像制作工作节点镜像启动工作节点启动控制节点遇到的问题 使用Docker 部署Jmeter非常方便,可以省略软件的安装以及配置,比如jdk、jmeter。需要部署多个工作节点可以节省时间。 制作Jmeter基础镜像 下载jmeter…...
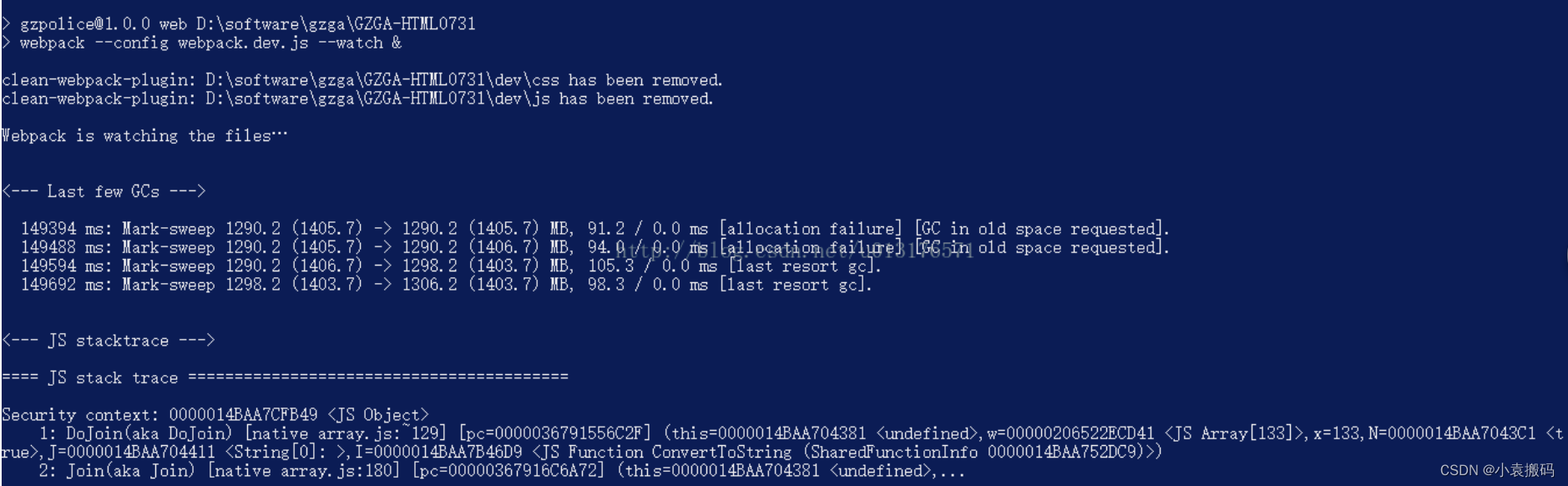
Vite与Webpack打包内存溢出问题优雅处理方式
Vite与Webpack打包内存溢出问题处理 文章目录 Vite与Webpack打包内存溢出问题处理1. Vite1. 打包错误提示2. 命令行方式解决3. 配置环境变量方式解决1. 设置变量2. 配置系统的环境变量 2. Webpack1. 打包错误提示2. 命令行方式解决3. 配置环境变量方式解决1. 设置变量2. 配置系…...

sqlalchemy——@listens_for
问:sqlalchemy如何实现:表中指定数据更新时,其time字段自动更新?答:使用listens_for 装饰器来注册事件监听器,确保在项目数据更新时触发相应的处理逻辑。 示例代码如下: # coding: utf-8 impo…...
MySQL进阶之锁(全局锁以及备份报错解决)
锁 全局锁 全局锁就是对整个数据库实例加锁,加锁后整个实例就处于只读状态,后续的DML的写语句,DDL语 句,已经更新操作的事务提交语句都将被阻塞。 其典型的使用场景是做全库的逻辑备份,对所有的表进行锁定ÿ…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...

Xcode 16 集成 cocoapods 报错
基于 Xcode 16 新建工程项目,集成 cocoapods 执行 pod init 报错 ### Error RuntimeError - PBXGroup attempted to initialize an object with unknown ISA PBXFileSystemSynchronizedRootGroup from attributes: {"isa">"PBXFileSystemSynchro…...
