【学习笔记】树上差分总结(点差分/边差分)
一.树上差分的基本概念
1.树上差分的定义
树上差分,顾名思义,意思就是在树上做差分。
至于什么是差分呢?如果不会的同学,可以先看看我的这篇博客:一维,二维差分の详解(简单易懂)_一维差分-CSDN博客
2.树上差分能解决的问题
树上差分有什么作用?举个例子,如果题目要求对树上的一段路径进行操作,并询问某个点或某条边被经过的次数,树上差分就可以派上用场了。
类比于差分数组,树上差分利用的思想也是前缀和思想。(在这里应该是子树和思想)
树上差分,就是利用差分的性质,对路径上的重要节点进行修改(而不是暴力全改),作为其差分数组的值,最后在求值时,利用dfs遍历求出差分数组的前缀和得出答案,就可以达到降低复杂度的目的。
树上差分时需要求LCA,不会的同学可以先看看我的这篇博客:详解最近公共祖先(LCA)-CSDN博客
树上差分一般有两种类型的题目,一种是对边进行差分,另一种就是对点进行差分。
下面我将会分别讲解一下这两种问题。
二.点差分
1.思路
直接去dfs暴力加点权的话,肯定会TLE,但是我们现在在讲啥?树上差分啊!
假设需要将两点u,v之间路径上的所有点权增加x,l是lca(u,v),p是l的父亲节点,则差分操作如下:
sum[u] += x;
sum[v] += x;
sum[l] -= x;
sum[p] -= x;举个栗子(其中假设x=1):

其中s和t就是题目中树上点权需要加1的节点的起始点,绿色的数字代表点权(已经加1了)
则操作后有:

至于为什么要这么操作呢?别急,继续往下看。
做完上述的差分操作后,我们就要统计答案了。
当我们dfs搜索到s,向上回溯。
下面以u表示当前dfs搜索到的节点。
对于每个u统计它的子树大小(要用前缀和的思想记录每个点的点权了),顺着路径标起来。
(即sum[u] += sum[son])
我们会发现第一次从s回溯到s与t的LCA时候,sum[LCA(s,t)] += sum[son[LCA(s,t)]]
此时sum[LCA(s,t)]=0(-1+1=0)。这时我们不禁会有一个疑问: "不是LCA(s,t)会被经过一次嘛,为什么是0!"
别急,我们继续搜另一边。.
继续:我们搜索到t,向上回溯。
依旧统计每个u的子树大小sum[u]+=sum[son]
再度回到LCA(s,t),依旧是sum[LCA(s,t)]+=sum[son[LCA(s,t)]]
这个时候 sum[LCA(s,t)]=1 这就达到了我们要的效果 (是不是特别优秀φ(゜▽゜*)♪)
但是我们还要思考一个问题:万一我们再从LCA(s,t)向上回溯的时候使得其父亲节点的子树和为1怎么办?这样我们不就使得其父亲节点被多经过了一次?
其实很简单,我们只需要在前面差分操作时将sum[fa[lca(s,t)]]-=x就行了。
这样就达到了标记我们路径上的点的要求! 是否有一种恍然大悟的感觉呢?

2.例题Max flow
问题

参考代码
#include<bits/stdc++.h>
using namespace std;
int n,q,mx[300001][41],deep[300001],sum[300001],ans;
vector<int> vec[300001];
void dfs(int x,int fa)//lca的初始化
{deep[x] = deep[fa] + 1;mx[x][0] = fa;for(int i = 0;i < vec[x].size();i++)if(vec[x][i] != fa)dfs(vec[x][i],x);
}
int lca(int x,int y)//倍增法求lca
{if(deep[x] < deep[y]) swap(x,y);for(int i = 40;i >= 0;i--)if(deep[mx[x][i]] >= deep[y])x = mx[x][i];if(x == y) return x;for(int i = 40;i >= 0;i--)if(mx[x][i] != mx[y][i]){x = mx[x][i];y = mx[y][i];}return mx[x][0];
}
void dfss(int x,int fa)//统计答案的最大值
{for(int i = 0;i < vec[x].size();i++){int t = vec[x][i];if(t == fa) continue;dfss(t,x);sum[x] += sum[t];//在树上进行类似于前缀和的操作}ans = max(ans,sum[x]);//取最大值
}
signed main()
{cin>>n>>q;for(int i = 1;i < n;i++){int u,v;scanf("%d%d",&u,&v);vec[u].push_back(v);vec[v].push_back(u);}dfs(1,0);for(int j = 1;j <= 40;j++)for(int i = 1;i <= n;i++)mx[i][j] = mx[mx[i][j - 1]][j - 1];while(q--){int u,v;cin>>u>>v;int l = lca(u,v);sum[u]++;//树上差分sum[v]++;sum[l]--;if(l != 1) sum[mx[l][0]]--;//如果l有父节点就进行后面的操作}dfss(1,0);cout<<ans;return 0;
}三.边差分
1.思路
思想其实和点差分是一样的,我来讲一下操作。
设将两点s,t之间路径上的所有边权增加x,l=LCA(s,t),以每条边两端深度较大的节点存储该边的差分数组,则操作如下:
sum[s] += x;
sum[t] += x;
sum[l] -= 2 * x;举个栗子(其中假设x=1):

红色边为需要经过的边,绿色的数字代表经过次数。
但是由于我们不能储存边权,所以只能把边权塞给了点权,因此我们的图应该是这样的

这样的话我们只要把sum[s]++,sum[t]++,sum[lca(s,t)]-=2就可以实现差分操作了。
同样地,只要dfs一遍,遍历时统计以每个节点为根的树的节点的权值和,就是当前节点到父亲节点的边的最终权值了!
是不是很厉害
至于为什么点差分和边差分的操作不一样,很简单,请读者自己思考。
树上差分主要还是学习思想吧!
2.例题树上必经边--边差分
问题

参考代码
#include<bits/stdc++.h>
using namespace std;
int n,q,mx[300001][41],deep[300001],sum[300001],ans,k;
vector<int> vec[300001];
void dfs(int x,int fa)
{deep[x] = deep[fa] + 1;mx[x][0] = fa;for(int i = 0;i < vec[x].size();i++)if(vec[x][i] != fa)dfs(vec[x][i],x);
}
int lca(int x,int y)
{if(deep[x] < deep[y]) swap(x,y);for(int i = 40;i >= 0;i--)if(deep[mx[x][i]] >= deep[y])x = mx[x][i];if(x == y) return x;for(int i = 40;i >= 0;i--)if(mx[x][i] != mx[y][i]){x = mx[x][i];y = mx[y][i];}return mx[x][0];
}
void dfss(int x,int fa)
{for(int i = 0;i < vec[x].size();i++){int t = vec[x][i];if(t == fa) continue;dfss(t,x);sum[x] += sum[t];}
}
signed main()
{cin>>n>>q>>k;for(int i = 1;i < n;i++){int u,v;scanf("%d%d",&u,&v);vec[u].push_back(v);vec[v].push_back(u);}dfs(1,0);for(int j = 1;j <= 40;j++)for(int i = 1;i <= n;i++)mx[i][j] = mx[mx[i][j - 1]][j - 1];while(q--){int u,v;cin>>u>>v;int l = lca(u,v);sum[u]++;sum[v]++;sum[l] -= 2;}dfss(1,0);for(int i = 2;i <= n;i++)if(sum[i] == k)ans++;cout<<ans;return 0;
}四.BB in last
如果这篇博客对您有帮助的话,别忘了点赞收藏加关注支持一下吖~(小声BB)(o゚v゚)ノ

相关文章:

【学习笔记】树上差分总结(点差分/边差分)
一.树上差分的基本概念 1.树上差分的定义 树上差分,顾名思义,意思就是在树上做差分。 至于什么是差分呢?如果不会的同学,可以先看看我的这篇博客:一维,二维差分の详解(简单易懂)_一维差分-CSDN博客 2.树…...

Vue.js设计与实现(霍春阳)
Vue.js设计与实现 (霍春阳) 电子版获取链接:Vue.js设计与实现(霍春阳) 编辑推荐 适读人群 :1.对Vue.js 2/3具有上手经验,且希望进一步理解Vue.js框架设计原理的开发人员; 2.没有使用过Vue.js,但对Vue.js框架设计感兴趣…...
go消息队列RabbitMQ - 订阅模式-fanout
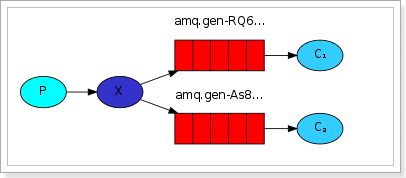
1、发布订阅 订阅模式,消息被路由投递给多个队列,一个消息被多个消费者获取。 1) 可以有多个消费者 2) 每个消费者有自己的queue(队列) 3) 每个队列都要绑定到Exchange(交换机&…...
)
科普类——5G远程实时操控技术在国内港口应用简介(十三)
在中国,5G远程实时操控技术已经在多个港口得到应用,并且应用规模不断扩大,展现出良好的发展前景。以下是一些具体的应用案例: 上港集团洋山港:上港集团与华为合作,在全球港口首次将F5G技术应用于超远程控制…...

整理:汉诺塔简析
大体上,要解决一个汉诺塔问题,就需要解决两个更简单的汉诺塔问题 以盘子数量 3 的汉诺塔问题为例 要将 3 个盘子从 A 移动到 C,就要: 将两个盘子从 A 移动到 B(子问题 1) 为了解决子问题 1,就…...

Android 8.1 设置--声音中增加通话音量
Android 8.1 设置--声音中增加通话音量 近来收到项目需求,想要在设置--声音中增加一项通话音量调节,具体修改参照如下: /vendor/mediatek/proprietary/packages/apps/MtkSettings/res/values/strings.xml <!-- Sound: Title for the opt…...
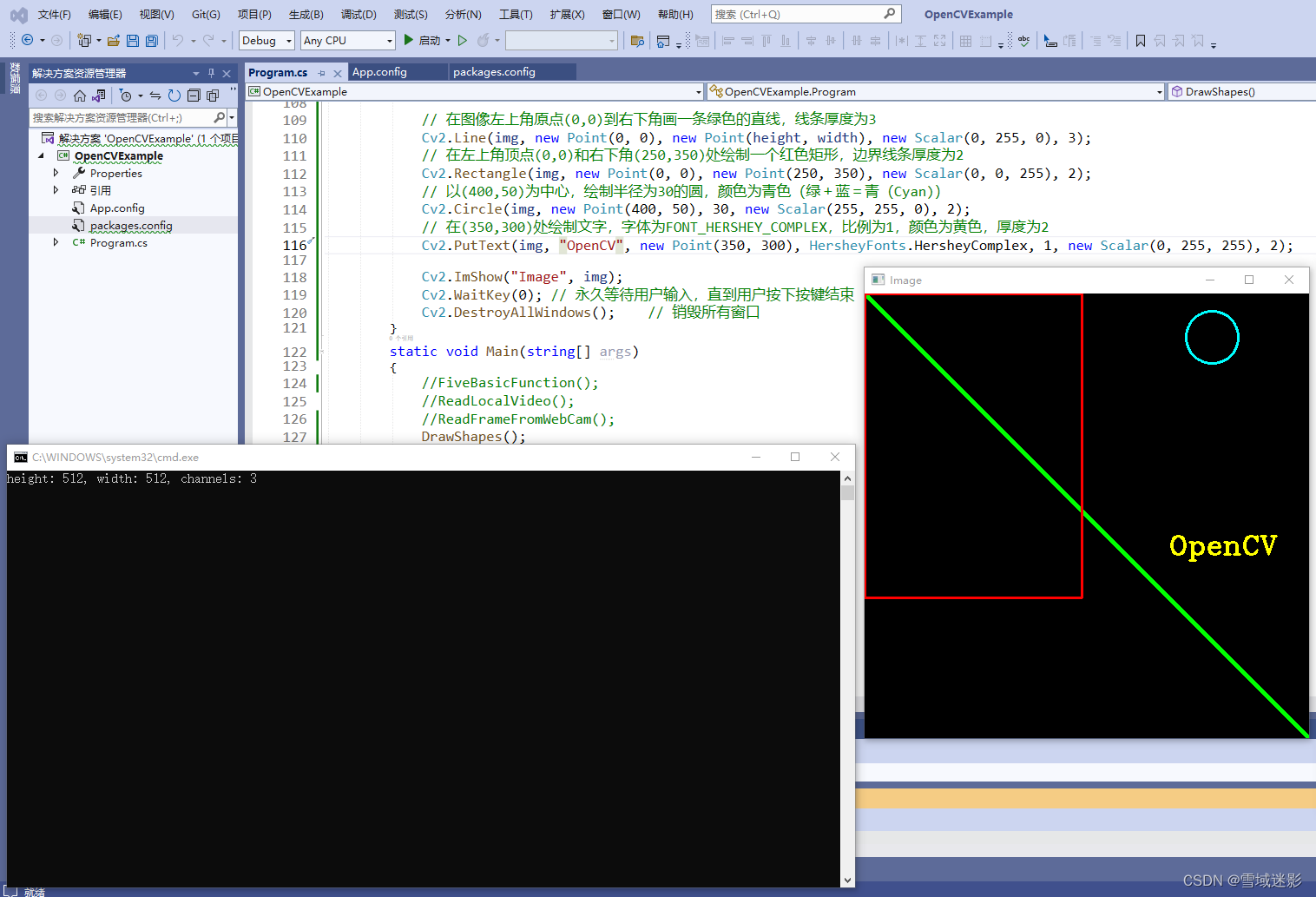
C#中使用OpenCvSharp4绘制直线、矩形、圆、文本
C#中使用OpenCvSharp4绘制直线、矩形、圆、文本 继之前的Python中使用Opencv-python库绘制直线、矩形、圆、文本和VC中使用OpenCV绘制直线、矩形、圆和文字,将之前的Python和C示例代码翻译成C#语言,很简单,还是借用OpenCvSharp4库中的Line、…...
Qt程序设计-自定义控件(提升法)
本文讲解如何使用提升法自定义控件,控件有界面。 实现自定义一个开关控件,控件上显示当前的状态。实现过程如下: 1、在创建的项目上,添加qt设计界面类。 2、选择widget 3、更改名称为MySwitchButton 4、添加两个图标资源文件,用来显示开关状态 5、添加两个label,一个…...

计算机网络基础知识笔记
1 HOST和PORT Claude-2-100k: 我来用简单的语言解释一下HOST和PORT这两个网络术语: HOST就是设备的IP地址,比如"127.0.0.1"就是我们本机的IP地址; PORT就是端口号,可以把它简单理解为设备上的门牌号。 举个类比,我们要给某个人发信件,需要知道…...

【iOS ARKit】2D肢体动作捕捉
人体肢体动作捕捉在动漫影视制作、游戏CG 动画、实时模型驱动中有着广泛的应用,利用 ARKit,无须额外的硬件设备即可实现 2D和3D人体一系列关节和骨骼的动态捕捉,由于移动AR 的便携性及低成本,必将促进相关产业的发展。 ARBody Tr…...

MAC word删除空白页
问题:MAC word删除空白页 解决: option删除键...

字面跳动前端面试题:React Hook为什么不能放在if/循环/嵌套函数里面?
答:首先,React Hooks 是为了简化组件逻辑和提高代码可读性而设计的。将 Hook 放在 if/循环/嵌套函数中会破坏它们的封装性和可预测性,使得代码更难维护和理解。同时,这样做也增加了代码的复杂度,可能会导致性能下降和潜…...
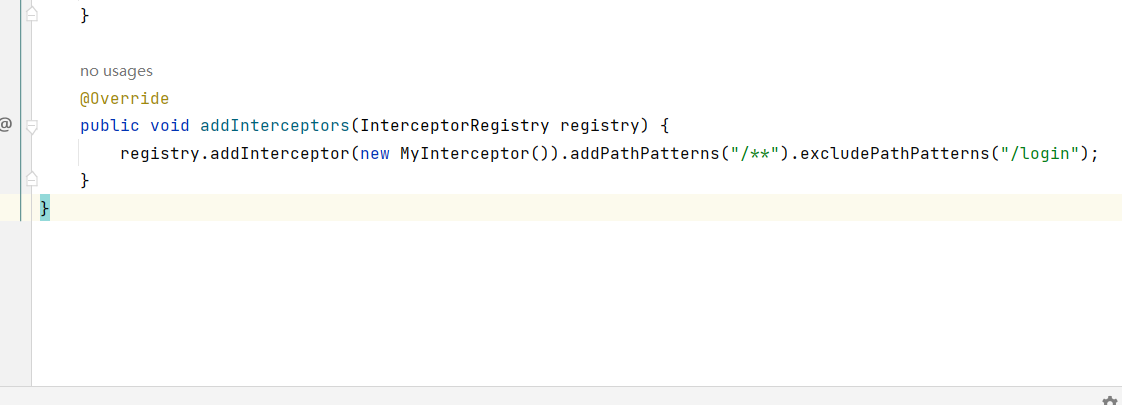
【SpringBoot】SpringBoot的web开发
📝个人主页:五敷有你 🔥系列专栏:SpringBoot ⛺️稳重求进,晒太阳 Wbe开发 使用Springboot 1)、创建SpringBoot应用,选中我们需要的模块; 2)、SpringBoot已经默…...

houdini 入门指南-参考自用,内有翻译错误
HOUDINI 18.5列1 GETTING STARTED 入门指南 What’s new in Houdini 18.5 胡迪尼18.5有什么新内容 New features and changes in Houdini 18.5.胡迪尼18.5的新功能和变化。Basics基础The basics of working with Houdini’s user interface.使用胡迪尼用户界面的基本知识。Shel…...

【笔记】SPN和PLMN 运营商网络名称显示
一、业务术语 缩写 全称 释义 CDNR Carrier Display Name Ressource 运营商显示名称资源 PLMN Public Land Mobile Network 公共陆地移动网络。 表示最终显示的网络运营商名字 SPN Service Provider Name SIM卡EF文件6F46。表示服务提供商名字,主要是SIM卡服务 OPL Operator …...
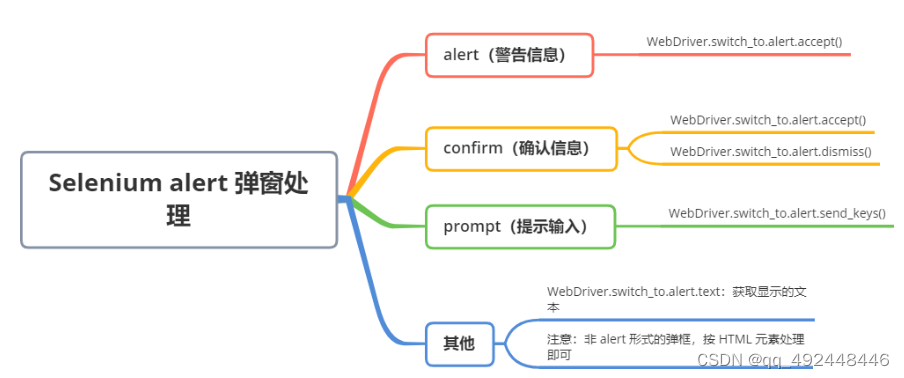
Selenium处理Alert弹窗
页面弹窗有 3 种类型: alert(警告信息) confirm(确认信息) prompt(提示输入) 对于页面出现的 alert 弹窗,Selenium 提供如下方法: 序号 方法/属性 描述 1 ac…...

FCIS 2023:洞悉网络安全新前沿,引领未来安全创新狂潮
在数字化浪潮席卷全球的今天,网络安全问题愈发凸显其重要性。 FCIS 2023网络安全创新大会作为业界瞩目的盛会,不仅汇聚了国际顶尖的网络安全专家,更展示了最前沿的安全技术与研究成果。那么,参与这场大会,我们究竟能学…...
4个最佳的免费全磁盘加密程序,总有一款适合你
全磁盘加密软件加密整个驱动器,而不仅仅是几个文件或文件夹。加密计算机的驱动器可以使你的私人数据免受窥探,即使你的计算机被盗。 你也不仅仅局限于一个硬盘驱动器。闪存驱动器和外部硬盘驱动器等外部设备也可以通过磁盘加密软件进行加密。 注意:Windows和macOS都集成了…...

SQL语句创建数据库
在SQL中,可以使用CREATE DATABASE语句来创建数据库。下面是一个示例: CREATE DATABASE database_name;其中,database_name是要创建的数据库的名称。你可以将其替换为你想要的数据库名称。 请注意,在不同的SQL数据库管理系统中&a…...

【lesson38】让minishell支持重定向
文章目录 minishell支持重定向minishell完整代码 minishell支持重定向 支持重定向的核心逻辑: 1.分析字符串是否含有重定向的符号,并且提取文件名。 #define INPUT_REDIR 0 //输入重定向 #define OUTPUT_REDIR 1 //输出重定向 #define APPEND_REDIR…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

鸿蒙Navigation路由导航-基本使用介绍
1. Navigation介绍 Navigation组件是路由导航的根视图容器,一般作为Page页面的根容器使用,其内部默认包含了标题栏、内容区和工具栏,其中内容区默认首页显示导航内容(Navigation的子组件)或非首页显示(Nav…...

P10909 [蓝桥杯 2024 国 B] 立定跳远
# P10909 [蓝桥杯 2024 国 B] 立定跳远 ## 题目描述 在运动会上,小明从数轴的原点开始向正方向立定跳远。项目设置了 $n$ 个检查点 $a_1, a_2, \cdots , a_n$ 且 $a_i \ge a_{i−1} > 0$。小明必须先后跳跃到每个检查点上且只能跳跃到检查点上。同时࿰…...
