Java 数据结构 二叉树(二)红黑树
目录
数据结构图-树
简介
规则
旋转
重新着色
红黑树构建过程
前言-与正文无关
生活远不止眼前的苦劳与奔波,它还充满了无数值得我们去体验和珍惜的美好事物。在这个快节奏的世界中,我们往往容易陷入工作的漩涡,忘记了停下脚步,感受周围的世界。让我们一起提醒自己,要适时放慢脚步,欣赏生活中的每一道风景,享受与家人朋友的温馨时光,发现那些平凡日子里隐藏的幸福时刻。因为,这些点点滴滴汇聚起来的,才是构成我们丰富多彩生活的本质。希望每个人都能在繁忙的生活中找到自己的快乐之源,不仅仅为了生存而工作,更为了更好的生活而生活。
送你张美图!希望你开心!

数据结构图-树

简介
红黑树是一种自平衡的二叉搜索树。在二叉搜索树中,树中的每个节点都有一个键值,且每个节点的键值都大于其左子树中任何节点的键值,并小于其右子树中任何节点的键值。红黑树增加了一些额外的属性来确保树保持平衡,这样任何时间的查找、插入和删除操作的最坏情况时间复杂度都保持在 O(log n)。
规则
红黑树必须遵循以下属性:
- 节点颜色: 每个节点要么是黑色,要么是红色。
- 根节点: 树的根节点是黑色的。最底层每个叶子节点(NIL节点,空节点)是黑色的。
- 红色节点规则: 如果一个节点是红色的,则其子节点必须是黑色的(即不允许连续的红色节点)。
- 黑色高度: 从任一节点到其任何叶子节点的所有路径上的黑色节点数量相同(平衡的关键)
- 新插入的节点为红色: 新插入节点默认为红色,插入后需要校验红黑树是否符合规则,不符合则需要进行平衡

为了维持这些属性,红黑树在插入新节点或删除节点后会通过旋转和重新着色来进行调整。
旋转
旋转: 当插入或删除节点导致红黑树的性质被破坏时,可以通过旋转来重新平衡树。旋转有两种:
- 左旋: 节点的右子节点上升到其位置,而原节点变成了这个右子节点的左子节点。
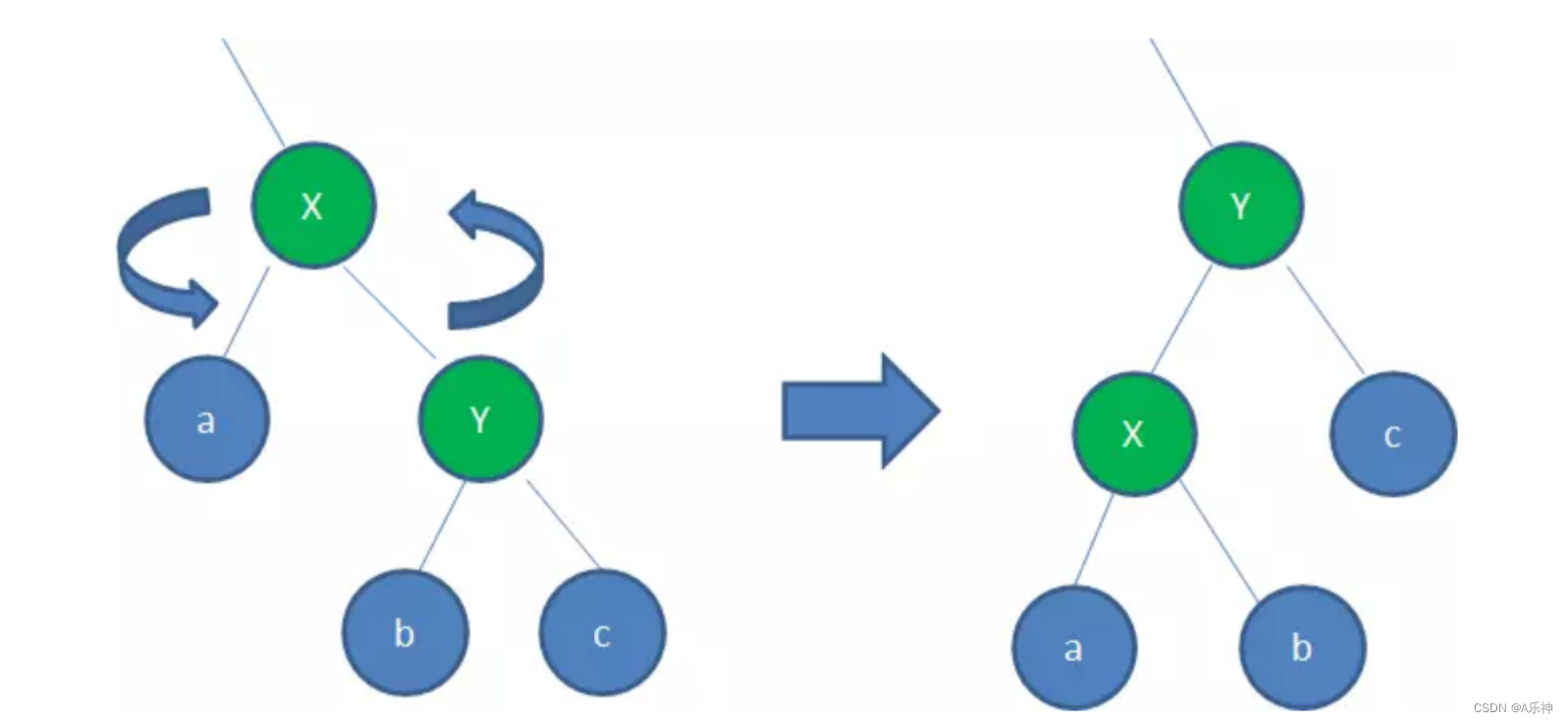
左旋操作将节点 Y旋转到节点 X 的位置,而节点 X 成为了 Y的左子节点。重要的是要注意,a节点比X小,成为x左节点,c同理还是在Y右边因为比Y大。b因为他是比Y小,按照规则他应该是在半边,又因为他比x大,所以在x右下面,这样左旋操作不会违反二叉搜索树的性质。
- 右旋: 节点的左子节点上升到其位置,而原节点变成了这个左子节点的右子节点。
右旋我就不细说了,和左旋类似,看左旋你应该就明白了

重新着色
如果节点的颜色导致红黑树性质被破坏(特别是连续红色节点的问题),则可以通过改变某些节点的颜色来修复。
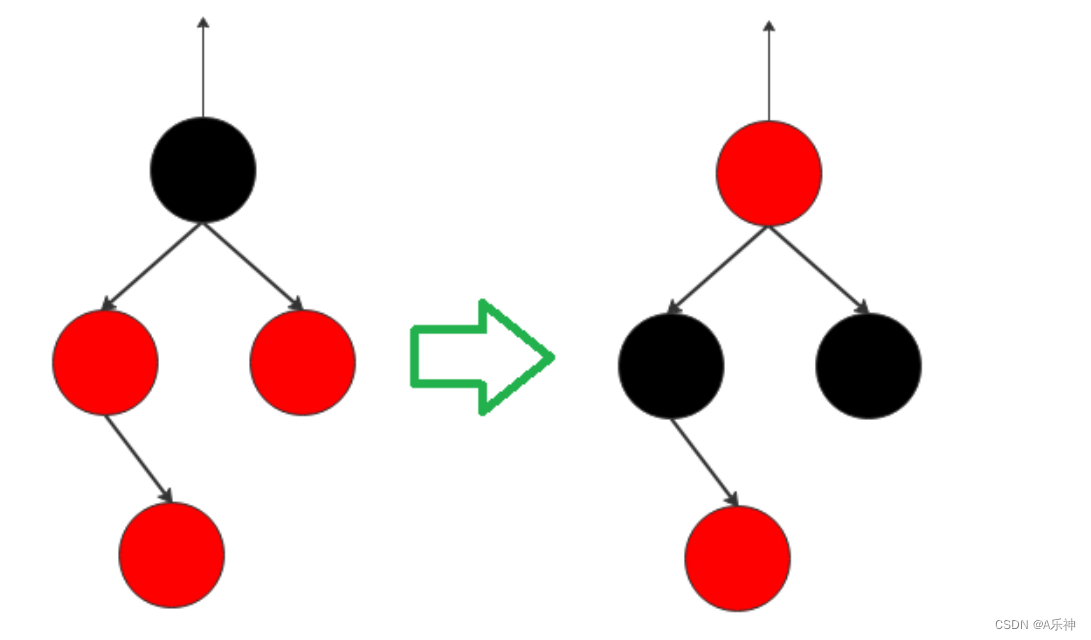
红黑树构建过程

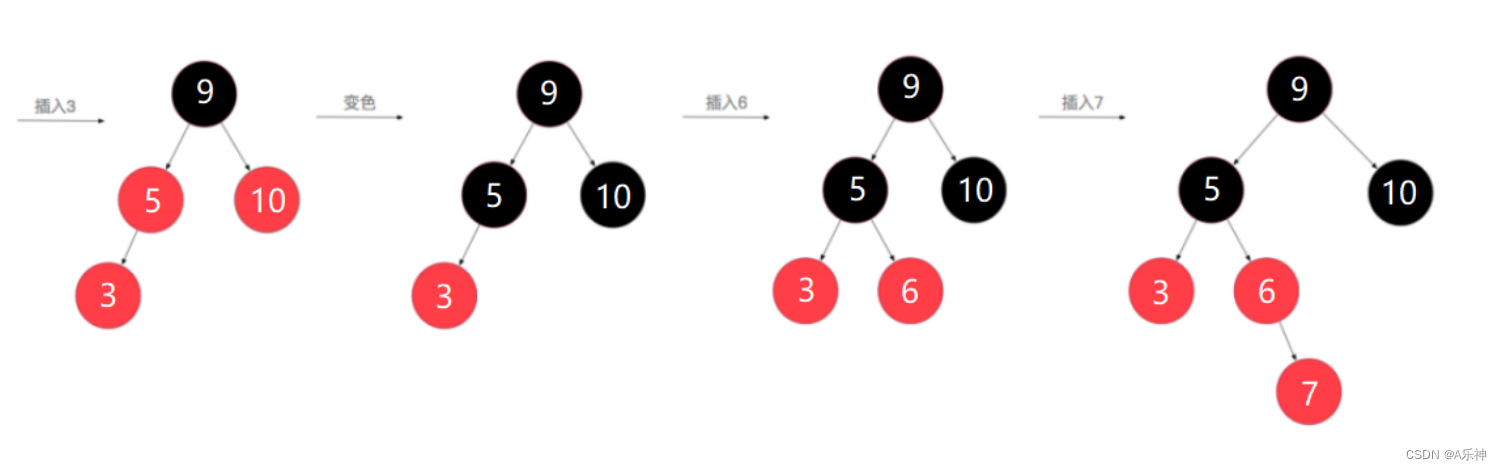
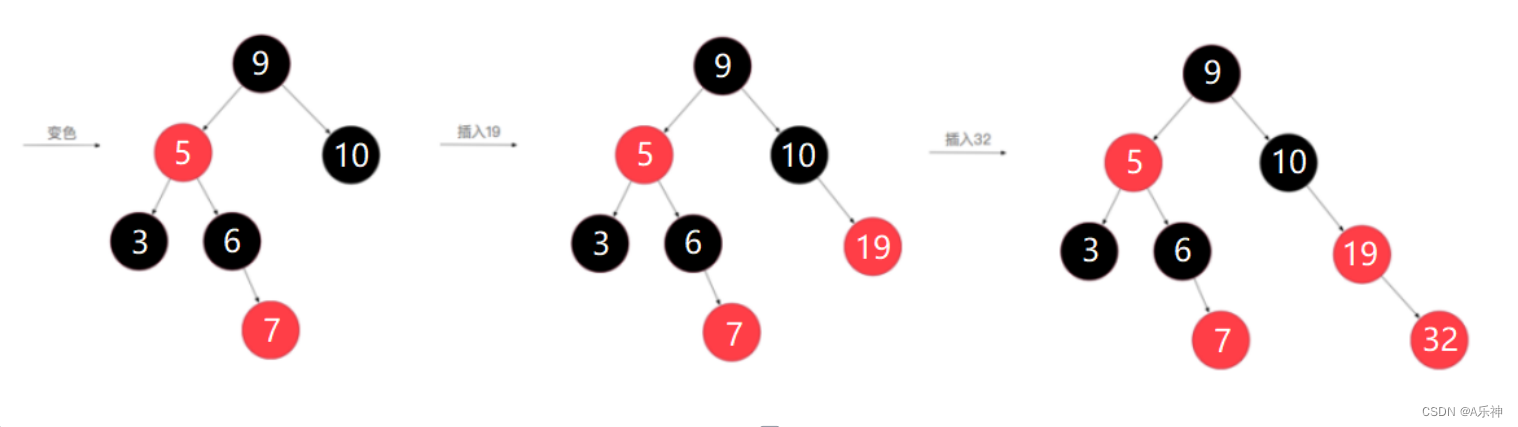
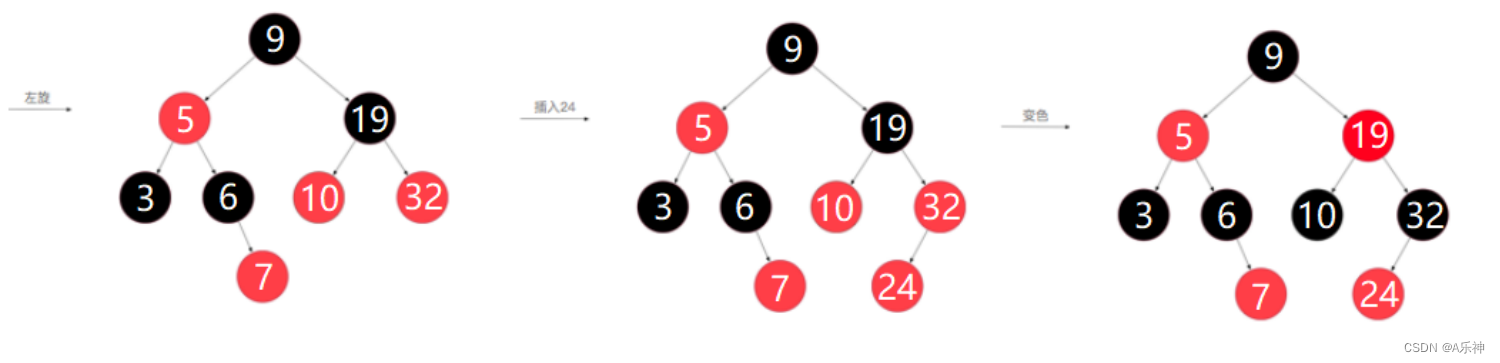
------------------------------------------与正文内容无关------------------------------------
如果觉的文章写对各位读者老爷们有帮助的话,麻烦点赞加关注呗!作者在这拜谢了!
混口饭吃了!如果你需要Java 、Python毕设、商务合作、技术交流、就业指导、技术支持度过试用期。请在关注私信我,本人看到一定马上回复!
这是我全部文章所在目录,看看是否有你需要的,如果遇到觉得不对地方请留言,看到后我会查阅进行改正。
A乐神-CSDN博客
相关文章:

Java 数据结构 二叉树(二)红黑树
目录 数据结构图-树 简介 规则 旋转 重新着色 红黑树构建过程 前言-与正文无关 生活远不止眼前的苦劳与奔波,它还充满了无数值得我们去体验和珍惜的美好事物。在这个快节奏的世界中,我们往往容易陷入工作的漩涡,忘记了停下脚步…...

React18-完成弹窗封装
弹框封装 用法 // 创建 userRef.current?.open(create) // 修改 userRef.current?.open(edit,values){/* 创建用户 */} <CreateUser mRef{userRef} update{} />组件暴露open方法 文档地址:https://react.dev/reference/react/useImperativeHandle useIm…...

蓝桥杯2024/1/31-----底层测试模板
和之前一样建好工程文件夹,里边包含User(放工程文件,mian.c)、Driver(存放底层文件如Led.c,Led.h等) 新建的工程先搭建框架,可以先书写底层函数(此次书写了四个函数并包含…...
-高精度-乘-低精度)
蓝桥杯备战(AcWing算法基础课)-高精度-乘-低精度
目录 前言 1 题目描述 2 分析 2.1 关键代码 2.2 关键代码分析 3 代码 前言 详细的代码里面有自己的理解注释 1 题目描述 给定两个非负整数(不含前导 00) A 和 B,请你计算 AB 的值。 输入格式 共两行,第一行包含整数 A&a…...

C++设计模式-里氏替换原则
里氏替换原则定义了继承规范。(封装、继承、多态) 定义1:类型S对象o1,类型T对象o2,o1换成o2时程序意图不变,那么S是T的子类。 定义2:使用子类不破坏父类的意图。 注意:如果子类不…...

compose LazyColumn + items没有自动刷新问题
val dataLists by remember { mutableStateOf(datas) } 数据更改后列表不刷新问题。 val dataLists by remember { mutableStateOf(datas) } LazyColumn(modifier Modifier.padding(top 5.dp)) {items(dataLists) {....}} 可以将mutableStateOf 改为mutableStateListOf解决…...

Java八大常用排序算法
1冒泡排序 对于冒泡排序相信我们都比较熟悉了,其核心思想就是相邻元素两两比较,把较大的元素放到后面,在一轮比较完成之后,最大的元素就位于最后一个位置了,就好像是气泡,慢慢的浮出了水面一样 Jave 实现 …...

编程笔记 html5cssjs 075 Javascript 常量和变量
编程笔记 html5&css&js 075 Javascript 常量和变量 一、JavaScript 变量二、JavaScript 常量三、示例:小结: 在JavaScript中,变量和常量是用来存储数据的占位符。它们的主要区别在于可变性:变量的值可以改变,而…...

题目 1159: 偶数求和
题目描述: 有一个长度为n(n<100)的数列,该数列定义为从2开始的递增有序偶数(公差为2的等差数列),现在要求你按照顺序每m个数求出一个平均值,如果最后不足m个,则以实际数量求平均值。编程输出该平均值序…...

呼吸灯--FPGA
目录 1.breath_led.v 2.tb_breath_led.v 呼吸灯就是从完全熄灭到完全点亮,再从完全点亮到完全熄灭。具体就是通过控制PWM的占空比控制亮灭程度。 绘制PWM波的步骤就是,首先灯是在第一个时钟周期保持高电平熄灭状态,在第二个时钟周期保持1/1…...
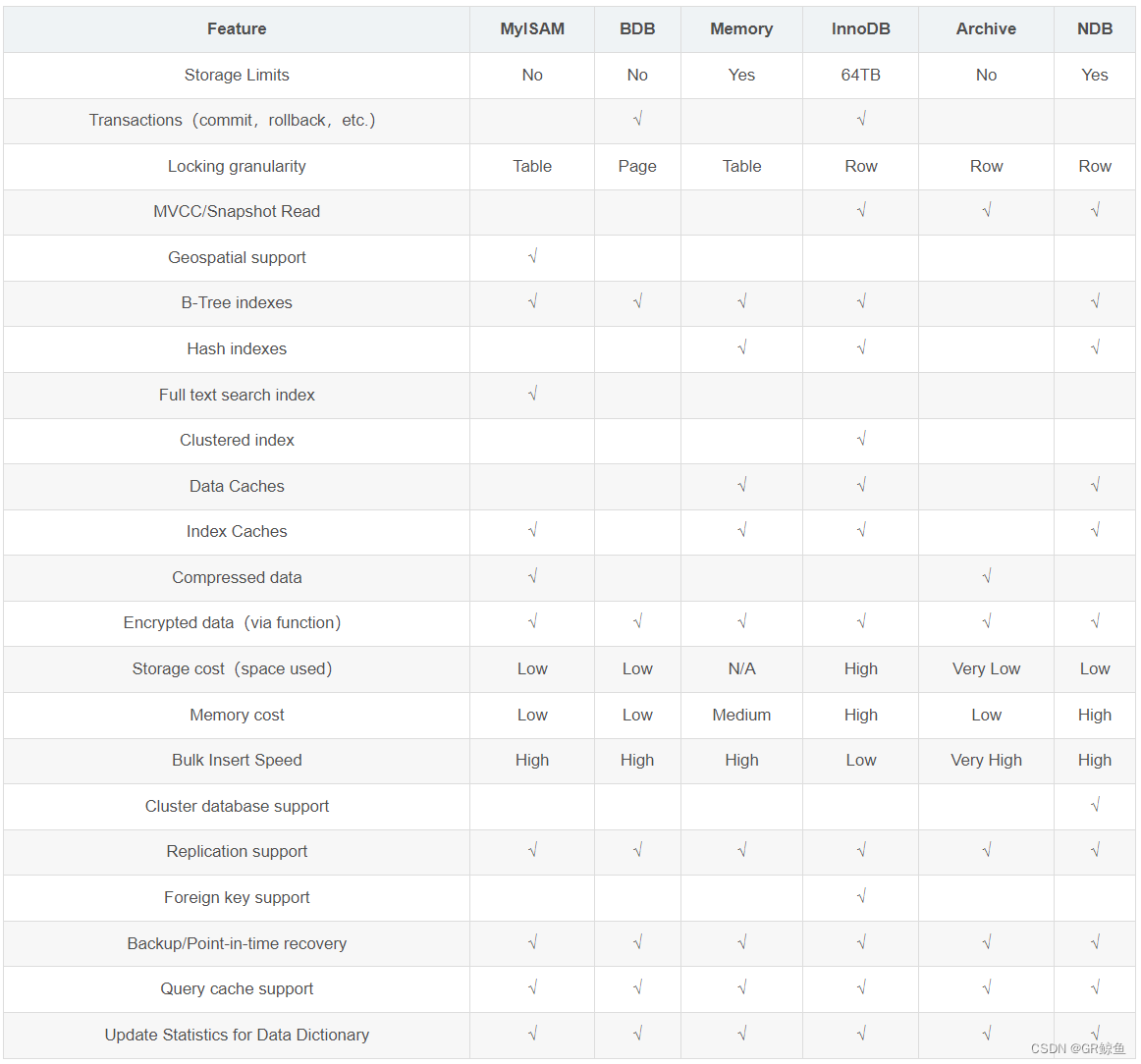
MySQL数据库①_MySQL入门(概念+使用)
目录 1. 数据库的概念 1.1 数据库的存储介质 1.2 主流数据库 2. MySQL的基本使用 2.1 链接数据库 2.2 服务器管理 2.3 数据库,服务器和表关系 2.4 简单MySQL语句 3. MySQL架构 4. SQL分类 5. 存储引擎 本篇完。 1. 数据库的概念 数据库是按照数据结构来…...
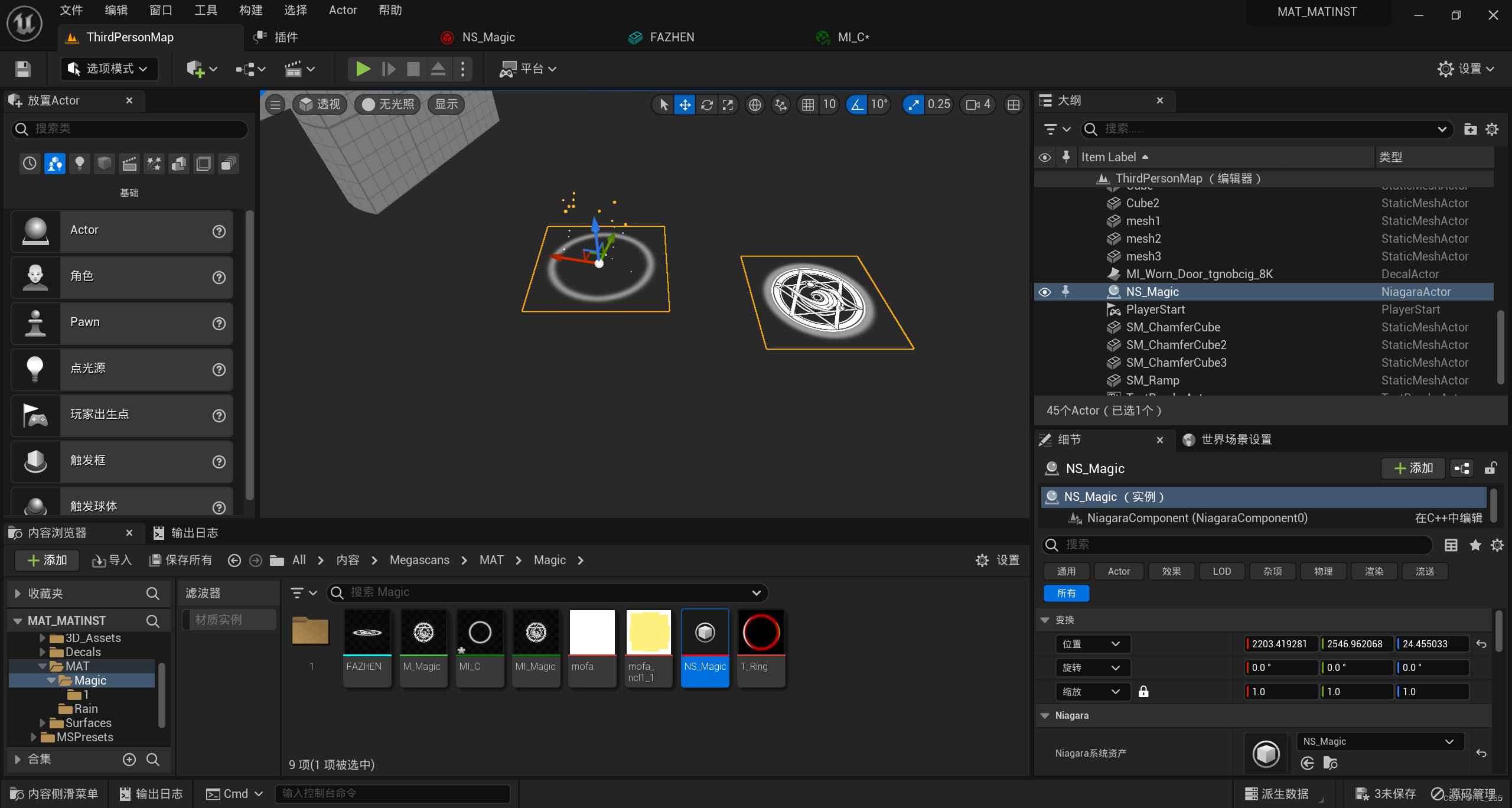
虚幻UE 特效-Niagara特效实战-魔法阵
回顾Niagara特效基础知识:虚幻UE 特效-Niagara特效初识 其他四篇实战:UE 特效-Niagara特效实战-烟雾、喷泉、 虚幻UE 特效-Niagara特效实战-火焰、烛火、 虚幻UE 特效-Niagara特效实战-雨天、 虚幻UE 特效-Niagara特效实战-眩晕。 本篇笔记记录了使用空模…...

Qt多语言翻译
Qt多语言翻译概述 Qt提供了非常简单易用的多语言翻译机制,其核心类为QTranslator.概括来说就是利用Qt的lupdate工具将项目中所有tr函数包裹的字符串提取到.ts文件中,然后使用Qt Linguist由专门的翻译人员对提取的.ts文件进行逐个单词短语的翻译工作. 翻译…...
Latex学习记录
目录 1.Latex各种箭头符号总结 2.[Latex]公式编辑,编号、对齐 3.Latex公式编号: 多行公式多编号,多行公式单编号 4.LaTex中输入空格以及换行 1.Latex各种箭头符号总结 箭头符号 - ➚ (piliapp.com)https://cn.piliapp.com/symbol/arrow/Latex各种箭头…...

你在做绩效考核,还是绩效管理?二者有什么区别
绩效考核,为什么99%都失败,最后一地鸡毛?败在指标! 绩效管理,为什么大多数企业都能成功,而且越做越好?成在目标! 丢掉层层指标,人人制定目标,这是企业重新定…...
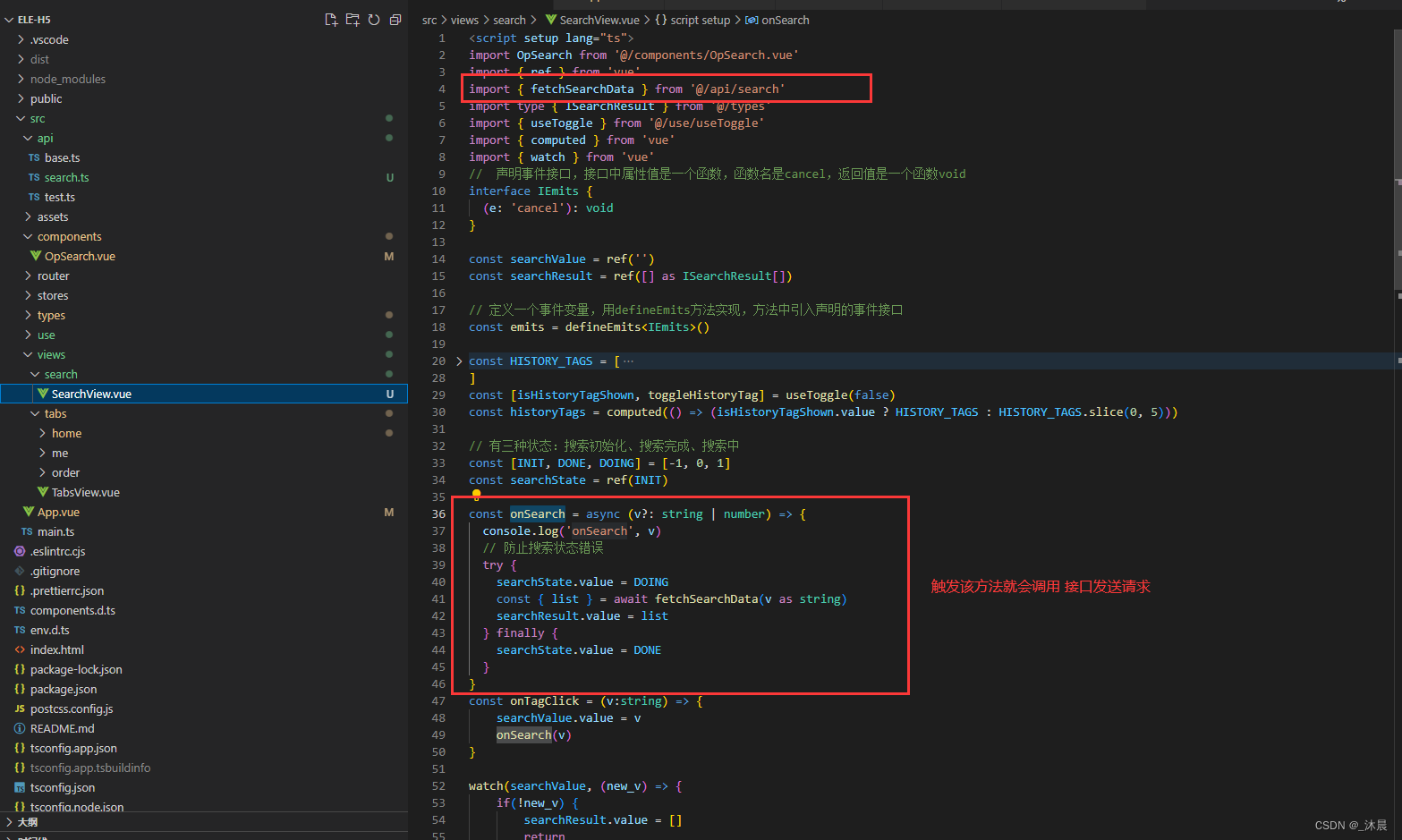
ele-h5项目使用vue3+vite+vant4开发:第四节、业务组件-SearchView组件开发
需求分析 展示切换动画搜索框输入文字,自动发送请求搜索结果展示搜索状态维护历史搜索展示,点击历史搜索后发送请求历史搜索更多切换动画效果 <script setup lang"ts"> import OpSearch from /components/OpSearch.vue import { ref } f…...

C系列-柔性数组
🌈个人主页: 会编程的果子君 💫个人格言:“成为自己未来的主人~” 目录 编辑 柔性数组 柔性数组的特点 柔性数组的使用 柔性数组的优势 柔性数组 也许你从来没有听说过柔性数组这个概念,但是它确实是存在的,C99中&#…...
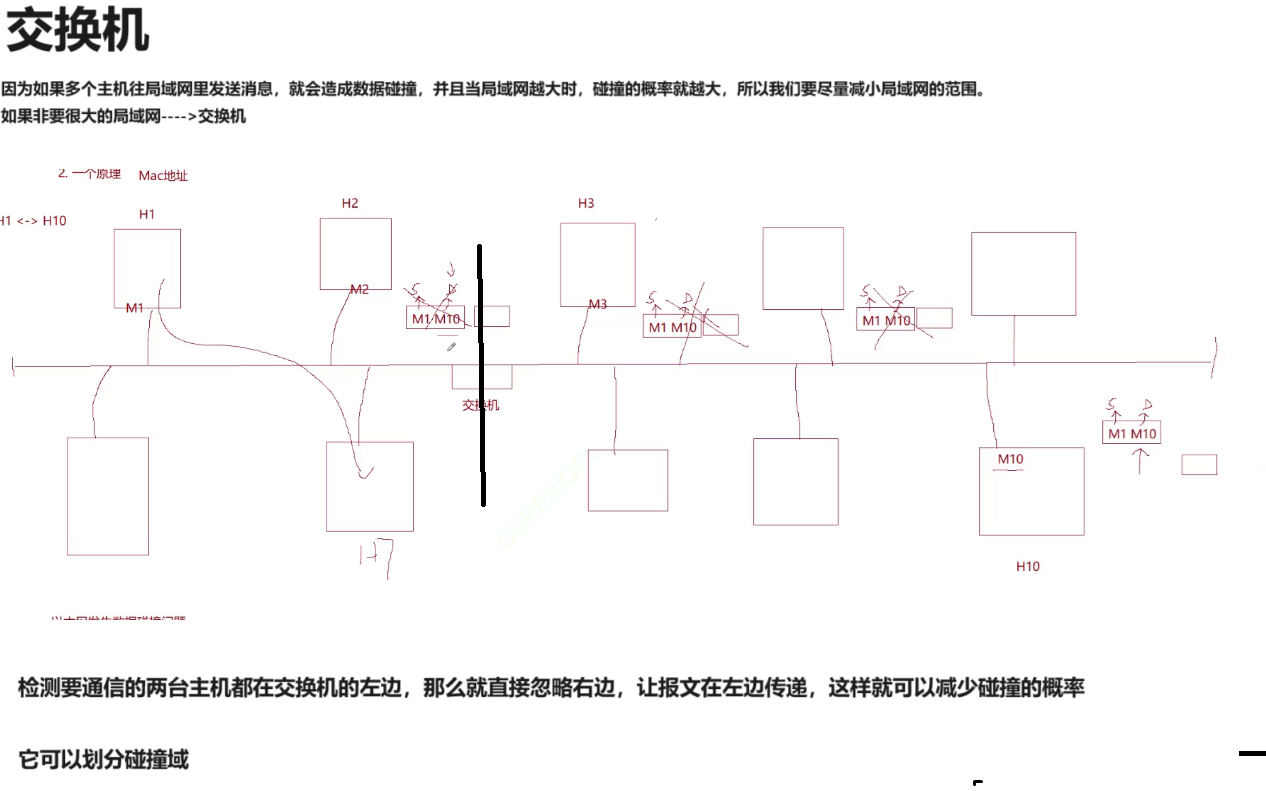
【Linux网络编程一】网络基础1(网络框架)
【Linux网络编程一】网络基础1(网络框架) 一.什么是协议1.通信问题2.协议本质3.网络协议标准 二.协议分层1.为什么协议要分层2.如何具体的分层 三.操作系统OS与网络协议栈的关系1.核心点:网络通信贯穿协议栈 四.局域网中通信的基本原理1.封装…...
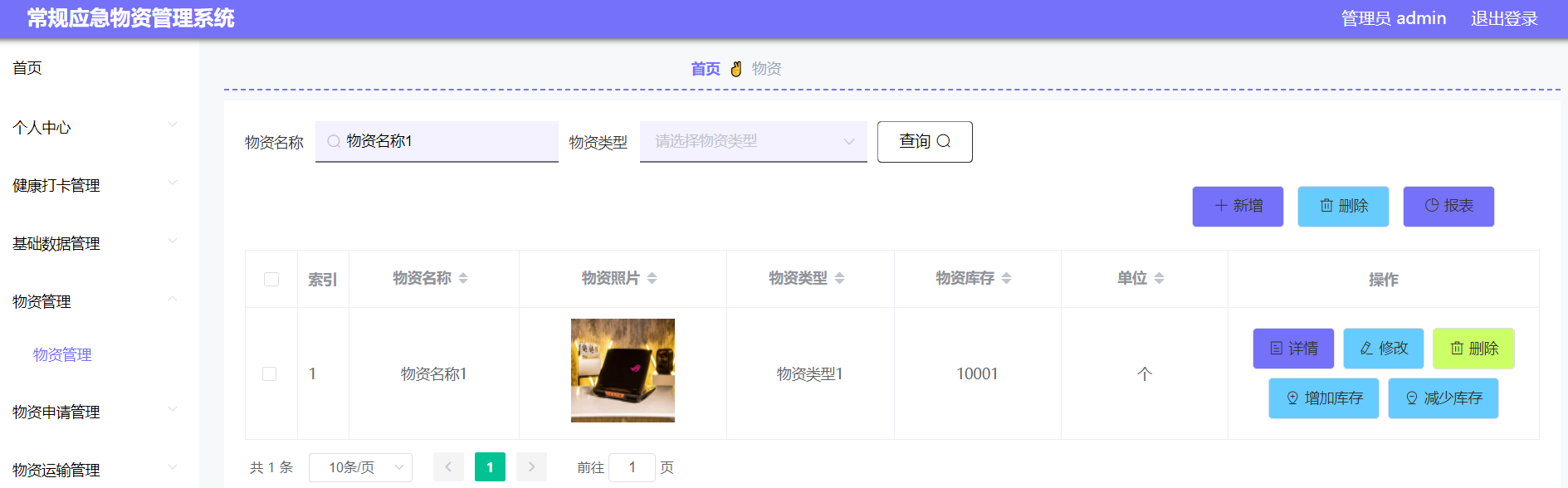
springboot156基于SpringBoot+Vue的常规应急物资管理系统
基于SpringBootVue的常规应急物资管理系统的设计与实现 摘 要 1 ABSTRACT 2 第一章 绪论 3 1.1研究背景 3 1.2研究意义 3 1.3国内外研究现状 4 1.3.1国外研究现状 4 1.3.2国内研究现状 4 1.4研究内容与方法 5 1.4.1研究内容 5 1.4.2研究方法 5 1.5论文的组织结构 5…...

学习MySQL的MyISAM存储引擎
学习MySQL的MyISAM存储引擎 MySQL的MyISAM存储引擎是MySQL早期版本中默认的存储引擎,后来被InnoDB所取代。尽管InnoDB在许多方面提供了更高级的特性,如事务处理、行级锁定和外键支持,MyISAM仍然因其简单性、高性能以及对全文搜索的支持而被广…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
