深度学习预备知识1——数据操作
所有机器学习方法都涉及从数据中提取信息,因此需要一些关于数据的实用技能,包括存储、操作和预处理数据。
机器学习通常需要处理大型数据集。线性代数和矩阵是计算大量数据的有力工具,需要一些矩阵运算相关的线性代数知识。
深度学习是关于优化的学习。 对于一个带有参数的模型,我们想要找到其中能拟合数据的最好模型。 在算法的每个步骤中,决定以何种方式调整参数需要一点微积分知识。(autograd包会自动计算微分)
机器学习还涉及如何做出预测:给定观察到的信息,某些未知属性可能的值是多少? 因此需要一些统计与概率论相关的知识。
1 数据操作
为了能够完成各种数据操作,我们需要某种方法来存储和操作数据。 通常,我们需要做两件重要的事:
- 获取数据
- 将数据读入计算机后对其进行处理
深度学习框架中的张量类(在MXNet中为ndarray, 在PyTorch和TensorFlow中为Tensor)都与Numpy的ndarray类似。 但深度学习框架又比Numpy的ndarray多一些重要功能:
- 首先,GPU很好地支持加速计算,而NumPy仅支持CPU计算
- 其次,张量类支持自动微分
1.1 初步使用
导入 torch
import torch
张量表示一个由数值组成的数组,这个数组可能有多个维度。 具有一个轴的张量对应数学上的向量(vector); 具有两个轴的张量对应数学上的矩阵(matrix); 具有两个轴以上的张量没有特殊的数学名称。
使用 arange 创建一个行向量 x。这个行向量包含以0开始的前12个整数,它们默认创建为整数。也可指定创建类型为浮点数。张量中的每个值都称为张量的 元素(element)。除非额外指定,新的张量将存储在内存中,并采用基于CPU的计算。
x = torch.arange(12)# tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
可以通过张量的shape属性来访问张量(沿每个轴的长度)的形状 。
x.shape# torch.Size([12])
如果只想知道张量中元素的总数,即形状的所有元素乘积,可以检查它的元素数量。
x.numel()# 12
要想改变一个张量的形状而不改变元素数量和元素值,可以调用reshape函数。虽然张量的形状发生了改变,但其元素值并没有变。 注意,通过改变张量的形状,张量的大小不会改变。
X = x.reshape(3, 4)# tensor([[ 0, 1, 2, 3],
# [ 4, 5, 6, 7],
# [ 8, 9, 10, 11]])
不需要通过手动指定每个维度来改变形状。 也就是说,如果我们的目标形状是(高度,宽度), 那么在知道宽度后,高度会被自动计算得出,不必我们自己做除法。在上面的例子中,为了获得一个3行的矩阵,我们手动指定了它有3行和4列。我们可以通过-1来调用此自动计算出维度的功能。 即我们可以用x.reshape(-1,4)或x.reshape(3,-1)来取代x.reshape(3,4)。
有时,我们希望使用全0、全1、其他常量,或者从特定分布中随机采样的数字来初始化矩阵。 我们可以创建一个形状为(2,3,4)的张量,其中所有元素都设置为0。
torch.zeros((2, 3, 4))# tensor([[[0., 0., 0., 0.],
# [0., 0., 0., 0.],
# [0., 0., 0., 0.]],
# [[0., 0., 0., 0.],
# [0., 0., 0., 0.],
# [0., 0., 0., 0.]]])
同样,我们可以创建一个形状为(2,3,4)的张量,其中所有元素都设置为1。
torch.ones((2, 3, 4))# tensor([[[1., 1., 1., 1.],
# [1., 1., 1., 1.],
# [1., 1., 1., 1.]],
# [[1., 1., 1., 1.],
# [1., 1., 1., 1.],
# [1., 1., 1., 1.]]])
有时我们想通过从某个特定的概率分布中随机采样来得到张量中每个元素的值。 例如,当我们构造数组来作为神经网络中的参数时,我们通常会随机初始化参数的值。 以下代码创建一个形状为(3,4)的张量。 其中的每个元素都从均值为0、标准差为1的标准高斯分布(正态分布)中随机采样。
torch.randn(3, 4)# tensor([[-0.0135, 0.0665, 0.0912, 0.3212],
# [ 1.4653, 0.1843, -1.6995, -0.3036],
# [ 1.7646, 1.0450, 0.2457, -0.7732]])
还可以通过提供包含数值的Python列表(或嵌套列表),来为所需张量中的每个元素赋予确定值。 在这里,最外层的列表对应于轴0,内层的列表对应于轴1。
torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])# tensor([[2, 1, 4, 3],
# [1, 2, 3, 4],
# [4, 3, 2, 1]])
1.2 运算符
在 tensor 上最简单的数学运算中最简单的且最有用的操作是按元素(elementwise)运算。它们将标准标量运算符应用于数组的每个元素。 对于将两个数组作为输入的函数,按元素运算将二元运算符应用于两个数组中的每对位置对应的元素。 我们可以基于任何从标量到标量的函数来创建按元素函数。
在数学表示法中,我们将通过符号 f : R → R f: \Bbb{R} \rightarrow \Bbb{R} f:R→R 来表示一元标量运算符(只接收一个输入)。这意味着该函数从任何实数( R \Bbb{R} R )映射到另一个实数。
同样,我们通过符号 f : R , R → R f: \Bbb{R}, \Bbb{R} \rightarrow \Bbb{R} f:R,R→R 表示二元标量运算符,这意味着该函数接收两个输入,并产生一个输出。给定同一形状的任意两个向量 μ \mu μ 和 ν \nu ν 和二元运算符 f f f ,可以得到向量 c = F ( μ , ν ) c = F(\mu, \nu) c=F(μ,ν)。具体计算方法是: c i ← f ( μ i , ν i ) c_i \leftarrow f(\mu _i, \nu _i) ci←f(μi,νi),其中 c i , μ i , ν i c_i, \mu _i, \nu _i ci,μi,νi 分别是向量 c , μ , ν c, \mu, \nu c,μ,ν 中的元素。在这里,我们通过将标量函数升级为按元素向量运算来生成向量值 F : R d , R d → R d F: \Bbb{R} ^d, \Bbb{R} ^d \rightarrow \Bbb{R} ^d F:Rd,Rd→Rd。
对于任意具有相同形状的张量, 常见的标准算术运算符(+、-、*、/和**)都可以被升级为按元素运算。 我们可以在同一形状的任意两个张量上调用按元素操作。
“按元素”方式可以应用更多的计算,包括像求幂这样的一元运算符。
x = torch.tensor([1.0, 2, 4, 8])
torch.exp(x)# tensor([2.7183e+00, 7.3891e+00, 5.4598e+01, 2.9810e+03])
除了按元素计算外,还可以执行线性代数运算,包括向量点积和矩阵乘法。
也可以把多个张量连结(concatenate)在一起, 把它们端对端地叠起来形成一个更大的张量。 只需要提供张量列表,并给出沿哪个轴连结。
当我们沿行(轴-0,形状的第一个元素) 和按列(轴-1,形状的第二个元素)分别连结两个矩阵,第一个输出张量的轴-0长度(6)是两个输入张量轴-0长度的总和(3+3); 第二个输出张量的轴-1长度(8)是两个输入张量轴-1长度的总和(4+4)
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
torch.cat((X, Y), dim=0), torch.cat((X, Y), dim=1)# (tensor([[ 0., 1., 2., 3.],
# [ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.],
# [ 2., 1., 4., 3.],
# [ 1., 2., 3., 4.],
# [ 4., 3., 2., 1.]]),
# tensor([[ 0., 1., 2., 3., 2., 1., 4., 3.],
# [ 4., 5., 6., 7., 1., 2., 3., 4.],
# [ 8., 9., 10., 11., 4., 3., 2., 1.]]))
通过逻辑运算符构建二元张量。 以X == Y为例: 对于每个位置,如果X和Y在该位置相等,则新张量中相应项的值为1。 这意味着逻辑语句X == Y在该位置处为真,否则该位置为0。
X == Y# tensor([[False, True, False, True],
# [False, False, False, False],
# [False, False, False, False]])
对张量中的所有元素进行求和,会产生一个单元素张量。
X.sum()# tensor(66.)
1.3 广播机制
在某些情况下,即使形状不同,我们仍然可以通过调用 广播机制(broadcasting mechanism)来执行按元素操作。 这种机制的工作方式如下:
- 通过适当复制元素来扩展一个或两个数组,以便在转换之后,两个张量具有相同的形状
- 对生成的数组执行按元素操作
在大多数情况下,我们将沿着数组中长度为1的轴进行广播:
a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
由于a和b分别是 3x1 和 1x2 的矩阵,如果让它们相加,它们的形状不匹配。 我们将两个矩阵广播为一个更大的 3x2 矩阵,矩阵a将复制列, 矩阵b将复制行,然后再按元素相加:
a + b# tensor([[0, 1],
# [1, 2],
# [2, 3]])
1.4 索引和切片
张量中的元素可以通过索引访问。第一个元素的索引是0,最后一个元素索引是-1; 可以指定范围以包含第一个元素和最后一个之前的元素。
可以用[-1]选择最后一个元素,可以用[1:3]选择第二个和第三个元素:
X[-1], X[1:3]# (tensor([ 8., 9., 10., 11.]),
# tensor([[ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.]]))
除读取外,我们还可以通过指定索引来将元素写入矩阵。
X[1, 2] = 9# tensor([[ 0., 1., 2., 3.],
# [ 4., 5., 9., 7.],
# [ 8., 9., 10., 11.]])
如果我们想为多个元素赋值相同的值,我们只需要索引所有元素,然后为它们赋值。 例如,[0:2, :]访问第1行和第2行,其中“:”代表沿轴1(列)的所有元素。 虽然我们讨论的是矩阵的索引,但这也适用于向量和超过2个维度的张量。
X[0:2, :] = 12# tensor([[12., 12., 12., 12.],
# [12., 12., 12., 12.],
# [ 8., 9., 10., 11.]])
1.5 节省内存
运行一些操作可能会导致为新结果分配内存。例如,如果我们用Y = X + Y,我们将取消引用Y指向的张量,而是指向新分配的内存处的张量。
Python的id()函数提供内存中引用对象的确切地址。运行Y = Y + X后,我们会发现id(Y)指向另一个位置。 这是因为Python首先计算Y + X,为结果分配新的内存,然后使Y指向内存中的这个新位置。
before = id(Y)
Y = Y + X
id(Y) == before# False
注意:
- 首先,我们不想总是不必要地分配内存。在机器学习中,我们可能有数百兆的参数,并且在一秒内多次更新所有参数。通常情况下,我们希望原地执行这些更新。
- 如果我们不原地更新,其他引用仍然会指向旧的内存位置,这样我们的某些代码可能会无意中引用旧的参数。
可以使用切片表示法将操作的结果分配给先前分配的数组,例如Y[:] = 。 创建一个新的矩阵Z,其形状与另一个Y相同, 使用zeros_like来分配一个全 0 的块。
Z = torch.zeros_like(Y)
print('id(Z):', id(Z))
Z[:] = X + Y
print('id(Z):', id(Z))# id(Z): 140327634811696
# id(Z): 140327634811696
如果在后续计算中没有重复使用X, 我们也可以使用X[:] = X + Y或X += Y来减少操作的内存开销。
before = id(X)
X += Y
id(X) == before# True
1.6 转换为其他Python对象
将深度学习框架定义的张量转换为NumPy张量(ndarray)。 torch张量和numpy数组将共享它们的底层内存,就地操作更改一个张量也会同时更改另一个张量。
A = X.numpy()
B = torch.tensor(A)
type(A), type(B)# (numpy.ndarray, torch.Tensor)
要将大小为1的张量转换为Python标量,可以调用item函数或Python的内置函数。
a = torch.tensor([3.5])
a, a.item(), float(a), int(a)# (tensor([3.5000]), 3.5, 3.5, 3)
相关文章:

深度学习预备知识1——数据操作
所有机器学习方法都涉及从数据中提取信息,因此需要一些关于数据的实用技能,包括存储、操作和预处理数据。 机器学习通常需要处理大型数据集。线性代数和矩阵是计算大量数据的有力工具,需要一些矩阵运算相关的线性代数知识。 深度学习是关于…...
【云原生运维问题记录】kubesphere登录不跳转问题
文章目录 现象问题排查 结论先行:kubesphere-system名称空间下reids宕机重启,会判断是否通过registry-proxy重新拉取镜像,该镜像原本是通过阿里云上拉取,代理上没有出现超时情况,导致失败。解决方案:删除re…...

深入学习Prometheus! 一款开源的监控和警报工具!
深入学习Prometheus! 一款开源的监控和警报工具! Prometheus是一个开源的监控和警报工具,它广泛用于记录和收集各种指标(如硬件资源使用情况、应用性能等),并提供强大的查询语言以帮助用户分析和查看这些数据。本文将…...

【webrtc】跟webrtc学list遍历
m98 代码:RTT G:\CDN\rtcCli\m98\src\video\call_stats.cc遍历list 进行删除 :remove_if void RemoveOldReports(int64_t now, std::list<CallStats::RttTime>* reports) {static constexpr const <...

网络安全产品之准入控制系统
文章目录 一、什么是准入控制系统二、准入控制系统的主要功能1. 接入设备的身份认证2. 接入设备的安全性检查 三、准入控制系统的工作原理四、准入控制系统的特点五、准入控制系统的部署方式1. 网关模式2. 控制旁路模式 六、准入控制系统的应用场景七、企业如何利用准入控制系统…...

为什么免费ip代理不适用于分布式爬虫?
费IP代理通常是一些公开免费提供的IP地址和端口,供用户免费使用。然而,这些免费IP代理并不适用于分布式爬虫的使用,原因如下: 1. 不稳定性 免费IP代理通常是由个人或组织提供的,没有稳定的维护和管理机制。因此&…...

【HTML 基础】元数据 meta 标签
文章目录 1. 设置字符集2. 描述网页内容3. 设置关键词4. 网页重定向5. 移动端优化注意事项结语 在网页开发中,<meta> 标签是一种十分重要的 HTML 元数据标签。通过巧妙使用 <meta> 标签,我们能够设置各种元数据,从而影响网页在浏…...
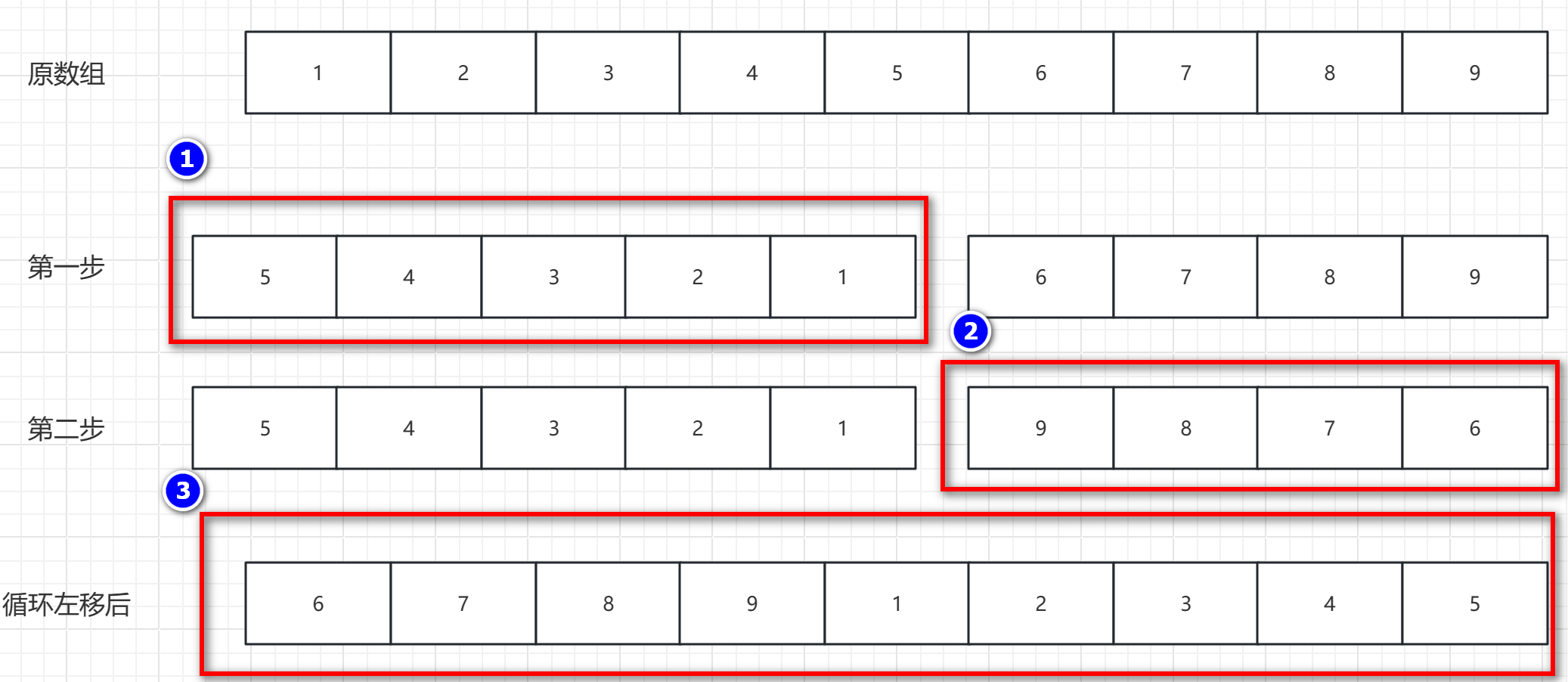
考研中常见的算法-逆置
元素逆置 概述:其实就是将 第一个元素和最后一个元素交换,第二个元素和倒数第二个元素交换,依次到中间位置。用途:可用于数组的移动,字符串反转,链表反转操作,栈和队列反转等操作。 逆置图解 …...

docker exec命令流程
背景 在使用docker时,我们经常会使用docker的很多命令,比如docker exec等创建容器并执行命令,那么你知道这条命令背后的原理吗,本文就来解析下这条命令大致的执行流程图 docker exec命令 首先我们按照启动docker之后࿰…...

游戏中好胜心的强化作用及其影响
在虚拟与现实交织的数字时代,电子游戏已经发展成为全球数以亿计玩家的日常娱乐和社交活动之一。其中,游戏体验往往激发并放大了参与者的好胜心理,这种现象不仅显著增强了游戏的吸引力,也在一定程度上塑造了玩家的行为模式和性格特…...
备战蓝桥杯---搜索(应用入门)
话不多说,直接看题: 显然,我们可以用BFS,其中,对于判重操作,我们可以把这矩阵化成字符串的形式再用map去存,用a数组去重现字符串(相当于map映射的反向操作)。移动空格先找…...

自学PyQt6杂记索引
文章目录 📖 介绍 📖🏡 安装 🏡📒 使用 📒📝 QtCore📝 QtGui📝 QtWidgets📝 QToolTip📝 信号和槽📝 QtDBus📝 QtNetwork📝 QtHelp📝 QtXml📝 QtSvg...

【Docker】Docker Registry(镜像仓库)
文章目录 一、什么是 Docker Registry二、镜像仓库分类三、镜像仓库工作机制四、常用的镜像仓库五、常用命令镜像仓库命令镜像命令(部分)容器命令(部分) 六、docker镜像仓库实战综合实战一:搭建一个 nginx 服务综合实战二:Docker hub上创建自己私有仓库综…...

TensorFlow2实战-系列教程14:Resnet实战2
🧡💛💚TensorFlow2实战-系列教程 总目录 有任何问题欢迎在下面留言 本篇文章的代码运行界面均在Jupyter Notebook中进行 本篇文章配套的代码资源已经上传 Resnet实战1 Resnet实战2 Resnet实战3 4、训练脚本train.py解读------创建模型 def …...

编程笔记 html5cssjs 069 JavaScript Undefined数据类型
编程笔记 html5&css&js 069 JavaScript Undefined数据类型 一、undefined数据类型二、类型运算小结 在JavaScript中,undefined 是一种基本数据类型,它表示一个变量已经声明但未定义(即没有赋值)或者一个对象属性不存在。 …...

《区块链简易速速上手小册》第6章:区块链在金融服务领域的应用(2024 最新版)
文章目录 6.1 金融服务中的区块链6.1.1 金融服务中区块链的基础6.1.2 主要案例:跨境支付6.1.3 拓展案例 1:去中心化金融(DeFi)6.1.4 拓展案例 2:代币化资产 6.2 区块链在支付系统中的作用6.2.1 支付系统中区块链的基础…...

【消息队列】kafka整理
kafka整理 整理kafka基本知识供回顾。...

python--杂识--16--代理密码中包含特殊字符
1 安装nginx 2 centos环境安装 yum install httpd-tools3 nginx.conf /etc/nginx/conf/nginx.conf #user nobody; worker_processes 1;#error_log logs/error.log; #error_log logs/error.log notice; #error_log logs/error.log info;#pid logs/nginx.pid;e…...
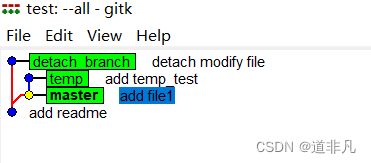
【Git】05 分离头指针
文章目录 一、分离头指针二、创建分支三、比较commit内容四、总结 一、分离头指针 正常情况下,在通过git checkout命令切换分支时,在命令后面跟着的是分支名(例如master、temp等)或分支名对应commit的哈希值。 非正常情况下&…...

【Tomcat与网络9】提高Tomcat启动速度的八大措施
本文我们来看一下如何对Tomcat进行调优,我们对于Tomcat的调优主要集中在三个方面:提高启动速度、提高系统稳定性和提高并发能力,后两者很多时候是相辅相成的,我们放在一起看。 Tomcat现在一般都嵌入在SpringBoot里,因…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...
