蓝桥杯刷题day05——2023
1、题目描述
请求出在12345678 (含) 至 98765432 (含) 中 ,有多少个数中完全不包含 2023。
完全不包含 2023是指 无论将这个数的哪些数位移除都不能得到2023。
例如 20322175,33220022 都完全不包含 2023,
而20230415,20193213 则含有 2023 (后者取第 1,2,6,8个数位) 。
2、解析
在给定数字范围内,完全不包含数字2023的所有数字的数量。
首先,我们需要明确什么是“完全不包含2023”。
这意味着无论我们移除这个数字的哪个部分,都不能得到数字2023。
例如,数字20322175和33220022都完全不包含2023,因为无论我们移除哪个部分,都不能得到2023。
但是,数字20230415和20193213则包含2023,因为如果我们移除某些部分,可以得到2023。
解题思路如下:
遍历给定的数字范围,即从12345678到98765432。
对于每个数字,尝试移除其各个部分,检查是否可以得到数字2023。
如果不能得到数字2023,则计数器加1。
返回计数器的值作为结果。
3、python代码
# count=0
# for n in range(12345678,98765433):
# ls = ["2", "0", "2", "3"]
# for i in ls:
# if i not in str(n):
# count+=1
# break
# else:
# for j in str(n):
# if ls:
# if j==ls[0]:
# ls.pop(0)
# else:
# break
# if ls:
# count+=1# print(count)print(85959030)相关文章:

蓝桥杯刷题day05——2023
1、题目描述 请求出在12345678 (含) 至 98765432 (含) 中 ,有多少个数中完全不包含 2023。 完全不包含 2023是指 无论将这个数的哪些数位移除都不能得到2023。 例如 20322175,33220022 都完全不包含 2023, 而20230415,20193213 …...

【51单片机】开发板和单片机的介绍(2)
前言 大家好吖,欢迎来到 YY 滴单片机系列 ,热烈欢迎! 本章主要内容面向接触过单片机的老铁 主要内容含: 欢迎订阅 YY滴C专栏!更多干货持续更新!以下是传送门! YY的《C》专栏YY的《C11》专栏YY的…...
《剑指 Offer》专项突破版 - 面试题 30 和 31:详解如何设计哈希表以及利用哈希表设计更加高级、复杂的数据结构
目录 一、哈希表的基础知识 二、哈希表的设计 2.1 - 插入、删除和随机访问都是 O(1) 的容器 2.2 - 最近最少使用缓存 一、哈希表的基础知识 哈希表是一种常见的数据结构,在解决算法面试题的时候经常需要用到哈希表。哈希表最大的优点是高效,在哈希表…...

回顾2023年及过去五年的成长经历
现在是2024年2月4日,我想回顾下过去两年的经历和感悟。总结下过去五年的成长经历。 最大的感悟就两点。第一,我相比于两年前成长了很多、也成熟了很多,不管是心智上还是心态上。而这些成长来自于读书、思考和结合实践的反思。第二࿰…...

99例电气实物接线及52个自动化机械手动图
给大家分享一些流水线设计中常见的一些结构,这些动态图很直观,有助于大家了解其原理,非常好懂。 1.家庭总电箱接线图 2.经典双控灯接线 3.五孔一开接线 4.电动机点动控制接线(不安全) 5.电动机自锁接线图(…...

SQL中聚合函数
SQL中的聚合函数是用于对一组值执行计算,并返回单个值的函数。它们通常在SELECT语句的SELECT列表中使用,并与GROUP BY子句结合使用来汇总数据。聚合函数忽略NULL值,只对非NULL值进行计算。以下是一些最常用的SQL聚合函数: 1. COU…...

深度学习预备知识1——数据操作
所有机器学习方法都涉及从数据中提取信息,因此需要一些关于数据的实用技能,包括存储、操作和预处理数据。 机器学习通常需要处理大型数据集。线性代数和矩阵是计算大量数据的有力工具,需要一些矩阵运算相关的线性代数知识。 深度学习是关于…...
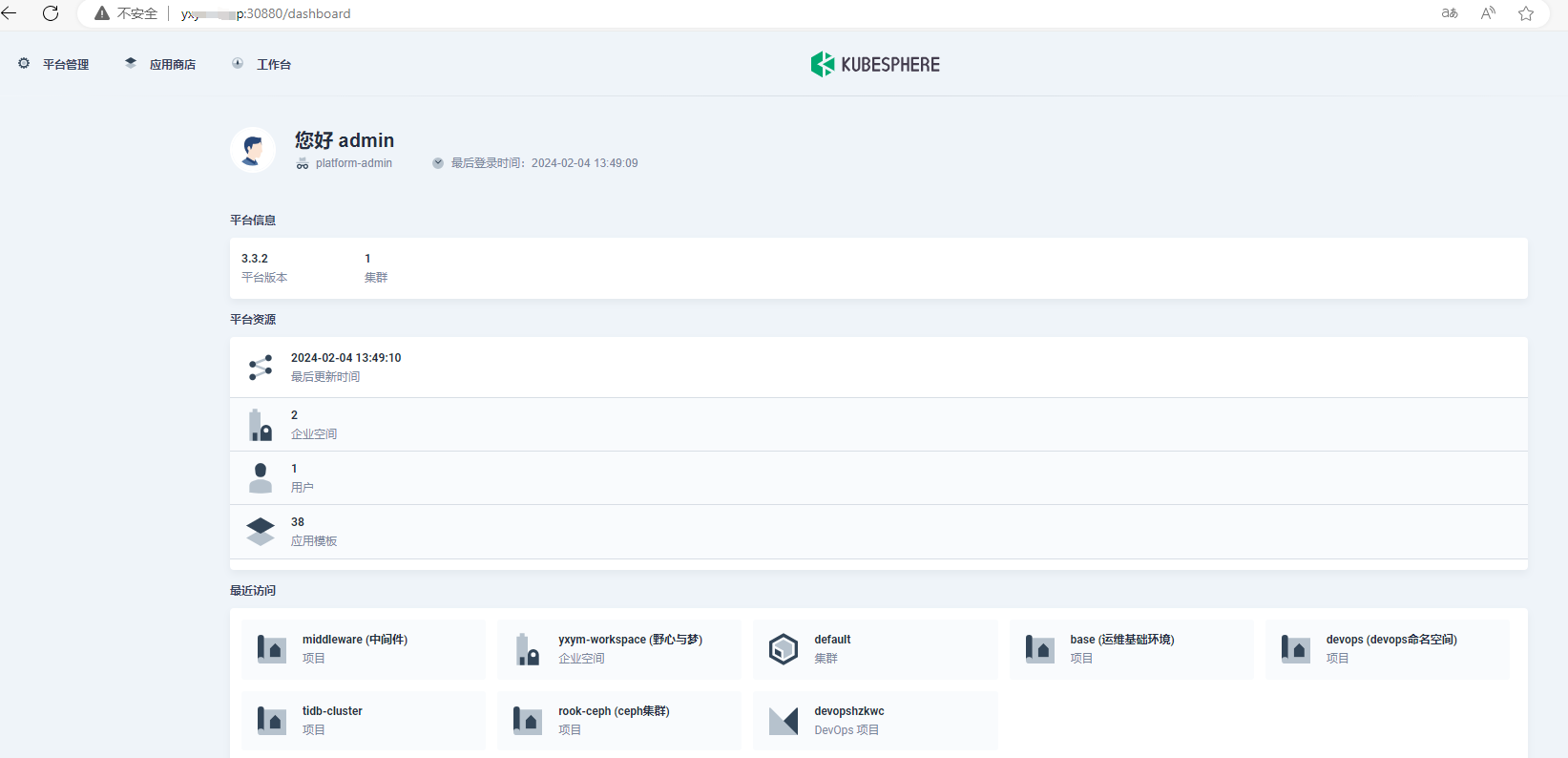
【云原生运维问题记录】kubesphere登录不跳转问题
文章目录 现象问题排查 结论先行:kubesphere-system名称空间下reids宕机重启,会判断是否通过registry-proxy重新拉取镜像,该镜像原本是通过阿里云上拉取,代理上没有出现超时情况,导致失败。解决方案:删除re…...

深入学习Prometheus! 一款开源的监控和警报工具!
深入学习Prometheus! 一款开源的监控和警报工具! Prometheus是一个开源的监控和警报工具,它广泛用于记录和收集各种指标(如硬件资源使用情况、应用性能等),并提供强大的查询语言以帮助用户分析和查看这些数据。本文将…...

【webrtc】跟webrtc学list遍历
m98 代码:RTT G:\CDN\rtcCli\m98\src\video\call_stats.cc遍历list 进行删除 :remove_if void RemoveOldReports(int64_t now, std::list<CallStats::RttTime>* reports) {static constexpr const <...

网络安全产品之准入控制系统
文章目录 一、什么是准入控制系统二、准入控制系统的主要功能1. 接入设备的身份认证2. 接入设备的安全性检查 三、准入控制系统的工作原理四、准入控制系统的特点五、准入控制系统的部署方式1. 网关模式2. 控制旁路模式 六、准入控制系统的应用场景七、企业如何利用准入控制系统…...

为什么免费ip代理不适用于分布式爬虫?
费IP代理通常是一些公开免费提供的IP地址和端口,供用户免费使用。然而,这些免费IP代理并不适用于分布式爬虫的使用,原因如下: 1. 不稳定性 免费IP代理通常是由个人或组织提供的,没有稳定的维护和管理机制。因此&…...

【HTML 基础】元数据 meta 标签
文章目录 1. 设置字符集2. 描述网页内容3. 设置关键词4. 网页重定向5. 移动端优化注意事项结语 在网页开发中,<meta> 标签是一种十分重要的 HTML 元数据标签。通过巧妙使用 <meta> 标签,我们能够设置各种元数据,从而影响网页在浏…...
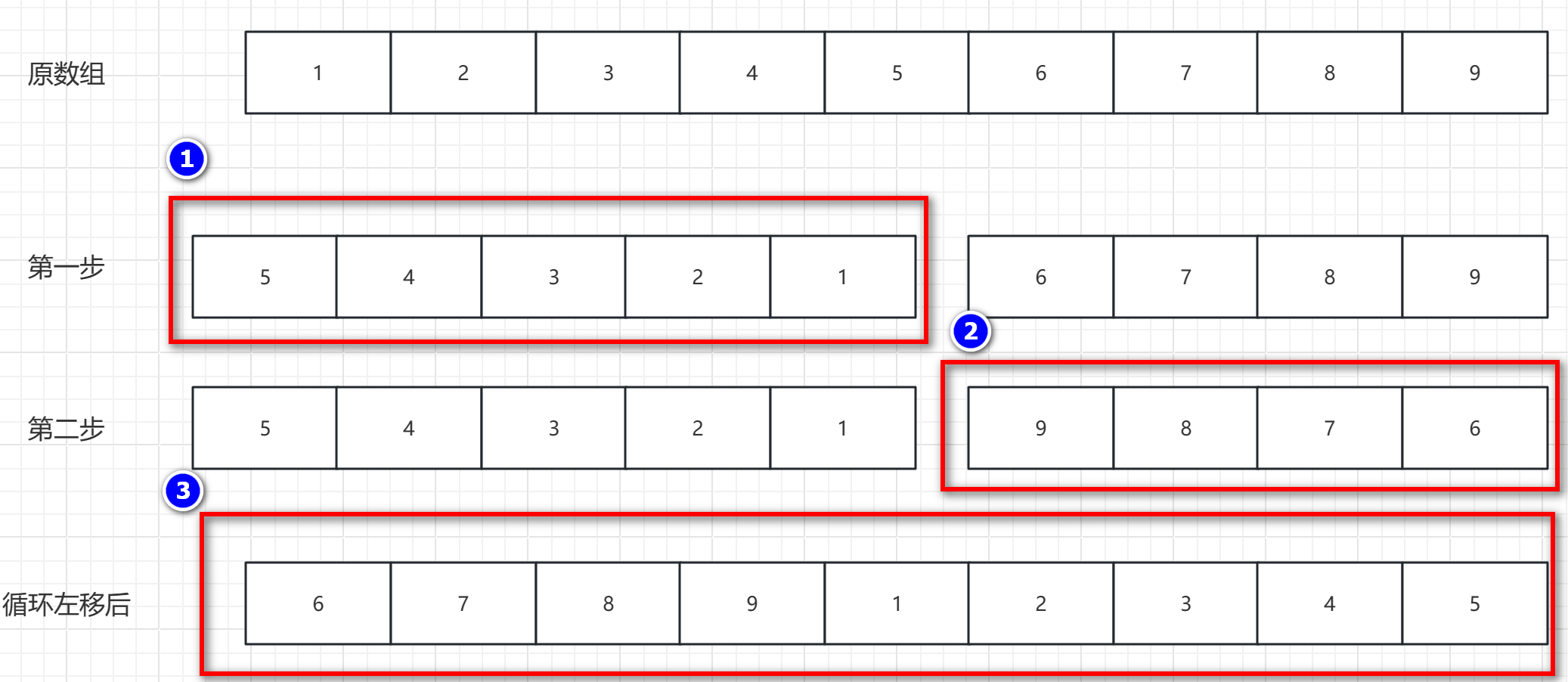
考研中常见的算法-逆置
元素逆置 概述:其实就是将 第一个元素和最后一个元素交换,第二个元素和倒数第二个元素交换,依次到中间位置。用途:可用于数组的移动,字符串反转,链表反转操作,栈和队列反转等操作。 逆置图解 …...

docker exec命令流程
背景 在使用docker时,我们经常会使用docker的很多命令,比如docker exec等创建容器并执行命令,那么你知道这条命令背后的原理吗,本文就来解析下这条命令大致的执行流程图 docker exec命令 首先我们按照启动docker之后࿰…...

游戏中好胜心的强化作用及其影响
在虚拟与现实交织的数字时代,电子游戏已经发展成为全球数以亿计玩家的日常娱乐和社交活动之一。其中,游戏体验往往激发并放大了参与者的好胜心理,这种现象不仅显著增强了游戏的吸引力,也在一定程度上塑造了玩家的行为模式和性格特…...
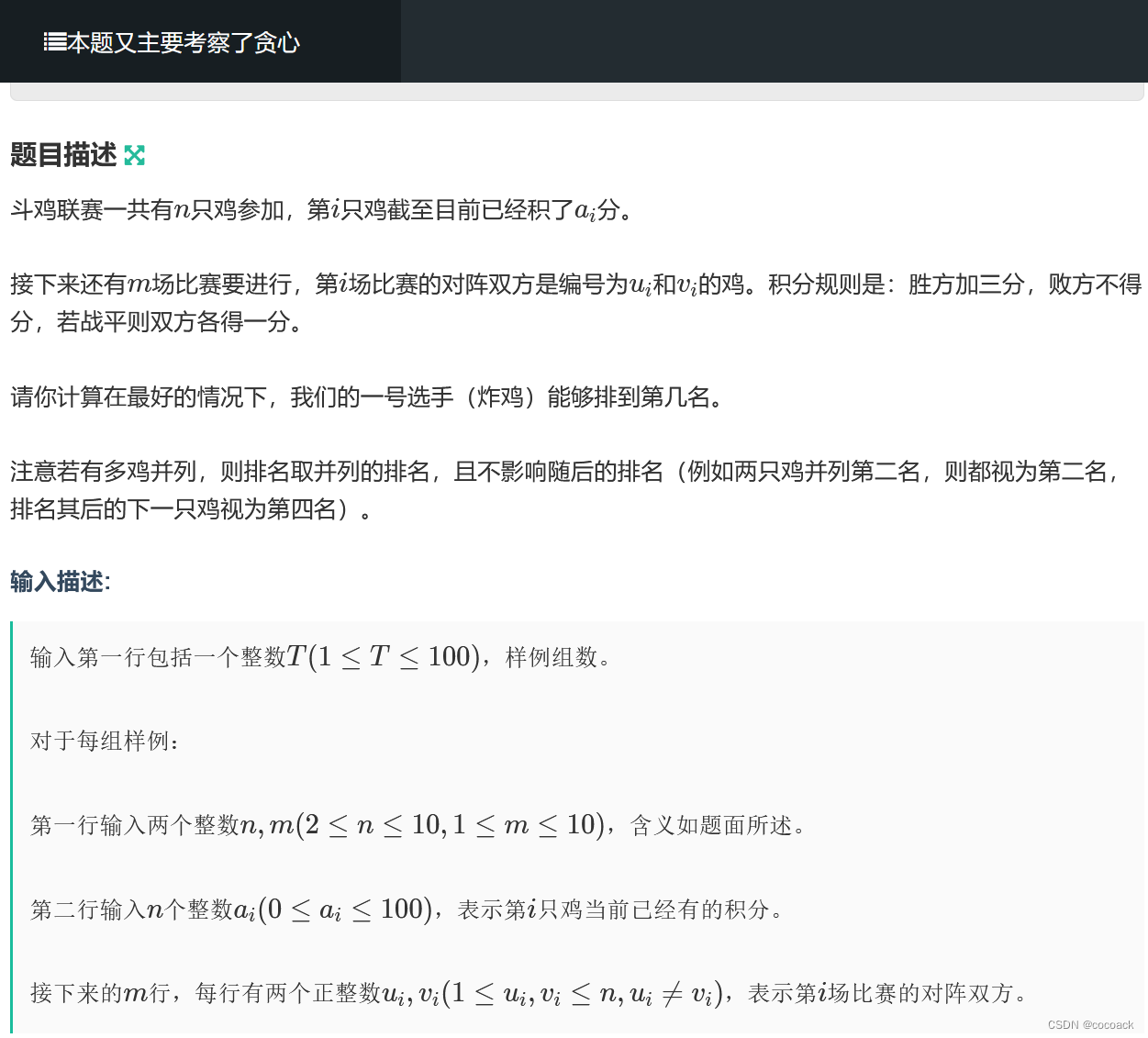
备战蓝桥杯---搜索(应用入门)
话不多说,直接看题: 显然,我们可以用BFS,其中,对于判重操作,我们可以把这矩阵化成字符串的形式再用map去存,用a数组去重现字符串(相当于map映射的反向操作)。移动空格先找…...

自学PyQt6杂记索引
文章目录 📖 介绍 📖🏡 安装 🏡📒 使用 📒📝 QtCore📝 QtGui📝 QtWidgets📝 QToolTip📝 信号和槽📝 QtDBus📝 QtNetwork📝 QtHelp📝 QtXml📝 QtSvg...

【Docker】Docker Registry(镜像仓库)
文章目录 一、什么是 Docker Registry二、镜像仓库分类三、镜像仓库工作机制四、常用的镜像仓库五、常用命令镜像仓库命令镜像命令(部分)容器命令(部分) 六、docker镜像仓库实战综合实战一:搭建一个 nginx 服务综合实战二:Docker hub上创建自己私有仓库综…...

TensorFlow2实战-系列教程14:Resnet实战2
🧡💛💚TensorFlow2实战-系列教程 总目录 有任何问题欢迎在下面留言 本篇文章的代码运行界面均在Jupyter Notebook中进行 本篇文章配套的代码资源已经上传 Resnet实战1 Resnet实战2 Resnet实战3 4、训练脚本train.py解读------创建模型 def …...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
