深度学习本科课程 实验1 Pytorch基本操作
一、Pytorch基本操作考察
1.1 任务内容
- 使用 𝐓𝐞𝐧𝐬𝐨𝐫 初始化一个 𝟏×𝟑 的矩阵 𝑴 和一个 𝟐×𝟏 的矩阵 𝑵,对两矩阵进行减法操作(要求实现三种不同的形式),给出结果并分析三种方式的不同(如果出现报错,分析报错的原因),同时需要指出在计算过程中发生了什么
- ① 利用 𝐓𝐞𝐧𝐬𝐨𝐫 创建两个大小分别 𝟑×𝟐 和 𝟒×𝟐 的随机数矩阵 𝑷 和 𝑸 ,要求服从均值为0,标准差0.01为的正态分布;② 对第二步得到的矩阵 𝑸 进行形状变换得到 𝑸 的转置 𝑸^𝑻 ;③ 对上述得到的矩阵 𝑷 和矩阵$ 𝑸^𝑻 $求矩阵相乘
- 给定公式 y 3 = y 1 + y 2 = x 2 + x 3 y_3=y_1+y_2=x^2 + x^3 y3=y1+y2=x2+x3,且 x = 1 x=1 x=1。利用学习所得到的Tensor的相关知识,求 y 3 y_3 y3对 x x x的梯度,即 d y 3 d x \dfrac{dy_3}{dx} dxdy3。要求在计算过程中,在计算 x 3 x^3 x3时中断梯度的追踪,观察结果并进行原因分析(可略)
1.2 任务思路及代码
步骤1: 矩阵生成与三种矩阵减法 ……
import torchX = torch.tensor([111,222,333])
Y = torch.tensor([[9999], [999]])
print(X)
print(Y)# 进行减法运算
temp1 = torch.tensor([10,10,10])
temp2 = torch.tensor([[10],[10]])
# 第一种方法
C1 = X - temp1
C2 = Y - temp2
print("-----1-----")
print(C1)
print(C2)
# 第二种方法
C1 = torch.sub(X, temp1)
C2 = torch.sub(Y, temp2)
print("-----2-----")
print(C1)
print(C2)
# 第三种方法
X.sub_(temp1)
Y.sub_(temp2)
print("-----3-----")
print(X)
print(Y)
实验结果分析
三种方法中, C = A - B与C = torch.sub(A, B)原理基本一致, 即对两个尺寸相同的矩阵(如果尺寸不同, torch将尝试广播机制), 进行每个元素对应的减法
第三种方法A.sub_(B)被称作原地操作, 前两种方法创建了新的Tensor对象来保存结果, 而原地操作将计算结果保留在了原对象上
比较而言, 非原地操作产生了额外的内存开销, 而原地操作直接修改了原对象, 后者的缺点在于丢失了原始数据
步骤2: 矩阵转置与乘法
# step1: 服从正态分布的随机数矩阵生成
P = 0.01 * torch.randn(3,2)
Q = 0.01 * torch.randn(4,2)
print("Matrix P :")
print(P)
print("Matrix Q :")
print(Q)
print("-------")
print()# step2: 矩阵的转置
Q_T = Q.t()
print("Q矩阵转置前:")
print(Q)
print("Q矩阵转置后:")
print(Q_T)
print("-------")
print()# step3: 矩阵的乘法
result = torch.mm(P, Q_T)
print("乘法结果:")
print(result)
实验结果分析
注: 矩阵的乘法除了调用.mm()方式外, 还可以使用torch.matmul()以及C = A @ B
步骤3: 梯度计算
# 正常的梯度计算
x = torch.tensor(1.0, requires_grad = True)y1 = x**2
y2 = x**3
y3 = y1 + y2
y3.backward()
gradient = x.grad
print("梯度为", gradient)
# 在计算x**3时中断梯度跟踪
x = torch.tensor(1.0, requires_grad = True)y1 = x**2
with torch.no_grad():y2 = x**3
y3 = y1 + y2
y3.backward()
gradient = x.grad
print("梯度为", gradient)
实验结果分析
由本实验提供的公式来看, 显然x为自变量, 计算梯度时应该对x进行跟踪
在定义时需要在x=1.0的基础上提交requires_grad = True
按顺序输入公式, 最后调用backward()函数即可计算梯度值
若要实现终端梯度跟踪, 则使用with torch.no_grad()语句
在本实验中, 计算$ x^3 时中断跟踪 , 意味着放弃考虑 时中断跟踪, 意味着放弃考虑 时中断跟踪,意味着放弃考虑 x^3 $项对函数梯度的贡献
因此, 原本梯度值为2+3=5, 现在计算为2 = 2
二、实现 logistic 回归
2.1 任务内容
- 要求动手从0实现 logistic 回归(只借助Tensor和Numpy相关的库)在人工构造的数据集上进行训练和测试,并从loss以及训练集上的准确率等多个角度对结果进行分析
(可借助nn.BCELoss或nn.BCEWithLogitsLoss作为损失函数,从零实现二元交叉熵为选作) - 利用 torch.nn 实现 logistic 回归在人工构造的数据集上进行训练和测试,并对结果进行分析,并从loss以及训练集上的准确率等多个角度对结果进行分析
……
2.2 任务思路及代码
import numpy as np
from IPython import display
from matplotlib import pyplot as plt
import random
np.random.seed(0)
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = torch.tensor(np.random.normal(0, 1, (num_examples, num_inputs)), dtype=torch.float)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float)def use_svg_display():# 用矢量图显示 display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):use_svg_display()# 设置图的尺寸plt.rcParams['figure.figsize'] = figsize
set_figsize()
plt.scatter(features[:, 1].numpy(), labels.numpy(), 1)def data_iter(batch_size, features, labels):num_examples = len(features)indices = list(range(num_examples))random.shuffle(indices) # 样本的读取顺序是随机的for i in range(0, num_examples, batch_size):j = torch.LongTensor(indices[i: min(i + batch_size, num_examples)]) # 最后一次可能不足一个batchyield features.index_select(0, j), labels.index_select(0, j)
def linreg(X, w, b):return torch.mm(X, w) + b
def squared_loss(y_hat, y): return (y_hat - y.view(y_hat.size())) ** 2 / 2
def sgd(params, lr, batch_size):for param in params:param.data -= lr * param.grad / batch_size
# 权重初始化
w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float32)
b = torch.zeros(1, dtype=torch.float32)
# 迭代求参数
w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True) # 模型训练
lr = 0.03
num_epochs = 3
batch_size = 10
net = linreg
loss = squared_loss
for epoch in range(num_epochs): # 训练模型一共需要num_epochs个迭代周期# 在每一个迭代周期中,会使用训练数据集中所有样本一次for X, y in data_iter(batch_size, features, labels):# x和y分别是小批量样本的特征和标签l = loss(net(X, w, b), y).sum() # l是有关小批量X和y的损失l.backward() # 小批量的损失对模型参数求梯度sgd([w, b], lr, batch_size) # 使用小批量随机梯度下降迭代模型参数w.grad.data.zero_() # 梯度清零b.grad.data.zero_()train_l = loss(net(features, w, b), labels)print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))print(true_w, '\n', w)
print(true_b, '\n', b)
实验结果分析
经过3轮的迭代后, 模型损失度<0.01%, 说明模型预测值与实际值相差非常小
从模型训练得到的参数来看, w值和b值的差距<0.03%, 说明模型训练结果良好
步骤2
lr = 0.03
import torch.utils.data as Data
batch_size = 10
# 将训练数据的特征和标签组合
dataset = Data.TensorDataset(features, labels)
# 把 dataset 放入 DataLoader
data_iter2 = Data.DataLoader(dataset=dataset, # torch TensorDataset formatbatch_size=batch_size, # mini batch sizeshuffle=True, # 是否打乱数据 (训练集一般需要进行打乱)num_workers=0, # 多线程来读数据,注意在Windows下需要设置为0
)
from torch import nn
class LinearNet(nn.Module):def __init__(self, n_feature):super(LinearNet, self).__init__()self.linear = nn.Linear(n_feature, 1)# forward 定义前向传播def forward(self, x):y = self.linear(x)return ynet = LinearNet(num_inputs)
# 模型参数初始化
from torch.nn import initinit.normal_(net.linear.weight, mean=0, std=0.01)
init.constant_(net.linear.bias, val=0) #也可以直接修改bias的data:net[0].bias.data.fill_(0)
# 选择损失函数
loss = nn.MSELoss()
# 选择优化算法(小批量随机梯度下降算法)
import torch.optim as optim
optimizer = optim.SGD(net.parameters(), lr=0.03) #梯度下降的学习率指定为0.03# 可以为不同的子网络设置不同学习率
# optimizer =optim.SGD([
# # 如果不指定学习率,则用默认的最外层学习率
# {'params': net.subnet1.parameters()}, # lr=0.03
# {'params': net.subnet2.parameters(), 'lr': 0.01}
# ], lr=0.03)num_epochs = 3
for epoch in range(1, num_epochs + 1):for X, y in data_iter2:output = net(X)l = loss(output, y.view(-1, 1))optimizer.zero_grad() # 梯度清零,等价于net.zero_grad()l.backward()optimizer.step()print('epoch %d, loss: %f' % (epoch, l.item()))# 定义准确率计算函数
def accuracy(y_hat, y): return (y_hat.argmax(dim=1) == y).float().mean().item()
def evaluate_accuracy(data_iter, net):acc_sum, n = 0.0, 0for X, y in data_iter:acc_sum = acc_sum + (net(X).argmax(dim=1) == y).float().sum().item()n += y.shape[0]return acc_sum / n# 定义均方误差计算函数
def calMSE(y_hat, y):return ((y_hat - y)**2).float().mean().item()
def evaluate_MSE(data_iter, net):MSE_sum, n = 0.0, 0for X, y in data_iter:MSE_sum = calMSE(net(X).argmax(dim=1), y)n += y.shape[0]return MSE_sum / n# 定义平均绝对误差函数
def calMAE(y_hat, y):return torch.abs(y_hat - y).float().mean().item()
def evaluate_MAE(data_iter, net):MAE_sum, n = 0.0, 0for X, y in data_iter:MAE_sum = calMAE(net(X).argmax(dim=1), y)n += y.shape[0]return MAE_sum / n
print("本模型的准确率:")
print(evaluate_accuracy(data_iter2, net))
print("本模型的MSE:")
print(evaluate_MSE(data_iter2, net))
print("本模型的MAE:")
print(evaluate_MAE(data_iter2, net))
2.3 实验结果分析
经过3轮迭代, 模型损失度loss<0.01%, 说明模型预测值与样本实际值相差非常小
然而, 准确度计算结果为0, 说明预测值与实际值完全不相等, 这主要是因为本任务是回归问题而不是分类问题
$ y$ 与 $ \hat{y} $ 的值域是一个连续的区间, 而不是离散的类型, 准确率计算函数可能不适用
如下例所示, 一次抽样中每个对应的元素相差基本处于$ [-0.001, 0.001] $, 却被判定为预测错误, 显然不合理
for X, y in data_iter2:print(X, y)print(net(X))print(net(X).argmax(dim=1) == y)print((net(X).argmax(dim=1) == y).float().mean().item())break
因此, 需要用其他特征来评价线性回归模型, 如均方误差和均方误差
M S E ≈ 0.039 MSE \approx 0.039 MSE≈0.039
M A E ≈ 0.006 MAE \approx 0.006 MAE≈0.006
从两个误差值来看, 预测误差非常小, 模型预测效果良好, 正确率高
三、实现 softmax 回归
3.1 任务内容
- 要求动手从0实现 softmax 回归(只借助Tensor和Numpy相关的库)在Fashion-MNIST数据集上进行训练和测试,并从loss、训练集以及测试集上的准确率等多个角度对结果进行分析(要求从零实现交叉熵损失函数)
利用torch.nn实现 softmax 回归在Fashion-MNIST数据集上进行训练和测试,并从loss,训练集以及测试集上的准确率等多个角度对结果进行分析
3.2 任务思路及代码
步骤1
引入库
import torchvision
import torchvision.transforms as transforms
mnist_train = torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST', train=True, download=True, transform=transforms.ToTensor())
mnist_test = torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST', train=False, download=True, transform=transforms.ToTensor())batch_size = 256
num_workers = 0
train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers)
test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers)
创建Softmax回归模型
class SoftmaxRegression(nn.Module):def __init__(self, input_size, num_classes):super(SoftmaxRegression, self).__init__()self.linear = nn.Linear(input_size, num_classes)def forward(self, x):return self.linear(x)
[num_features, num_classes] = [784, 10]
model = SoftmaxRegression(num_features, num_classes)
model = model.to('cuda')
定义损失函数和优化器
def cross_entropy_loss(y_hat, y):# 计算Softmaxexp_y_hat = torch.exp(y_hat)softmax = exp_y_hat / exp_y_hat.sum(dim=1, keepdim=True)# 选择目标类别的概率batch_size = y.size(0)predicted_probs = softmax[torch.arange(batch_size), y]# 计算交叉熵损失loss = -torch.log(predicted_probs)return loss.mean()criterion = cross_entropy_loss
optimizer = optim.SGD(model.parameters(), lr=0.1)
训练模型
num_epochs = 500
for epoch in range(num_epochs):for X, y in train_iter:# 前向传播X = X.view(X.size(0), -1)X = X.to('cuda')y = y.to('cuda')outputs = model(X)loss = criterion(outputs, y)# 反向传播和优化optimizer.zero_grad()loss.backward()optimizer.step()if (epoch + 1) % 10 == 0:print("当前轮数: ", epoch+1, "Loss: ", loss.item())
print("训练完毕!")
步骤2
测试模型
def eval_Accuracy(data_iter, model):acc_sum, n = 0.0, 0for X, y in data_iter:X = X.view(X.size(0), -1)# X.to('cuda')# y.to('cuda')acc_sum = acc_sum + (model(X).argmax(dim=1) == y).float().sum().item()n += y.shape[0]return acc_sum / n
model.to('cpu')
print(eval_Accuracy(test_iter, model))
3.3 实验结果分析
经过500轮迭代, 损失度为0.37, 其值较小, 说明预测值和样本值基本符合而略有偏差, 训练过程中损失度没有明显的下降, 可能是训练轮次不足导致的
训练集大小为60000, 测试集大小为10000, 本次训练耗时2个小时
如果对模型进行更高轮次的训练, 时间开销可能会过大
检验准确度为0.8439, 说明模型对输入数据分类正确度较高, 预测效果良好
相关文章:

深度学习本科课程 实验1 Pytorch基本操作
一、Pytorch基本操作考察 1.1 任务内容 使用 𝐓𝐞𝐧𝐬𝐨𝐫 初始化一个 𝟏𝟑 的矩阵 𝑴 和一个 𝟐𝟏 的矩阵 𝑵,对两矩阵…...
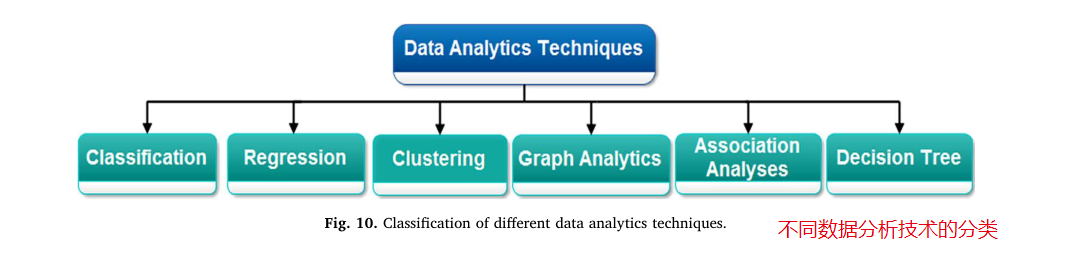
大数据分析|设计大数据分析的三个阶段
文献来源:Saggi M K, Jain S. A survey towards an integration of big data analytics to big insights for value-creation[J]. Information Processing & Management, 2018, 54(5): 758-790. 下载链接:链接:https://pan.baidu.com/s/1…...
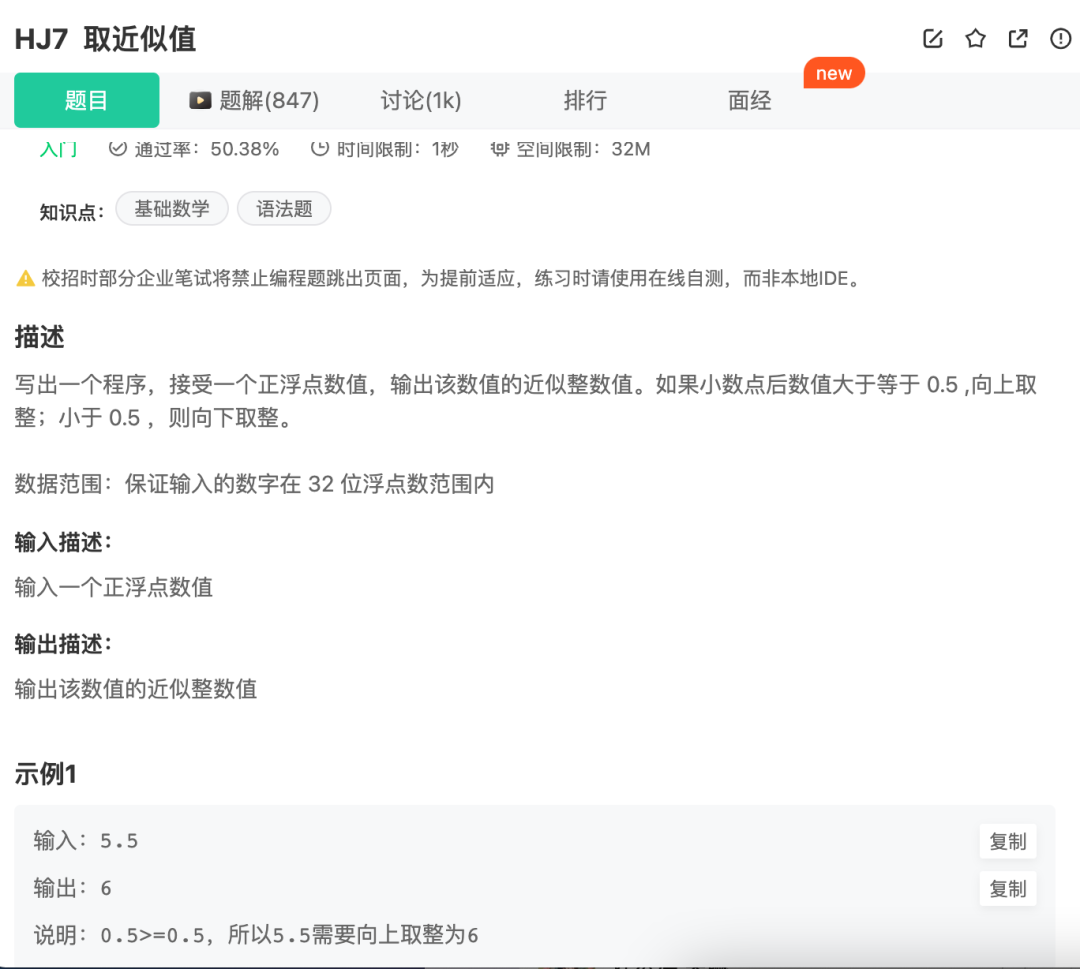
华为机考入门python3--(7)牛客7-取近似值
分类:数字 知识点: str转float float(str) 向上取整 math.ceil(float_num) 向下取整 math.floor(float_num) 题目来自【牛客】 import math def round_to_int(float_num): # 如果小数点后的数值大于等于0.5,则向上取整…...

C# Avalonia 11.0.6 绘图
在 Avalonia 11.0.6 中,Render 方法是被标记为 sealed 的,意味着不能直接在子类中重写这个方法。这样的设计可能是为了确保一致性和避免误用。 如果你需要在 Avalonia 中进行自定义的绘图操作,可以使用 DrawingContext,但是需要通…...
使用java -jar命令运行jar包提示“错误:找不到或无法加载主类“的问题分析
用maven把普通java项目打包成可运行的jar后,打开cmd用java -jar运行此jar包时报错: 用idea运行该项目则没有问题 。 其实原因很简单,我们忽略了2个细节。 java指令默认在寻找class文件的地址是通过CLASSPATH环境变量中指定的目录中寻找的。我…...
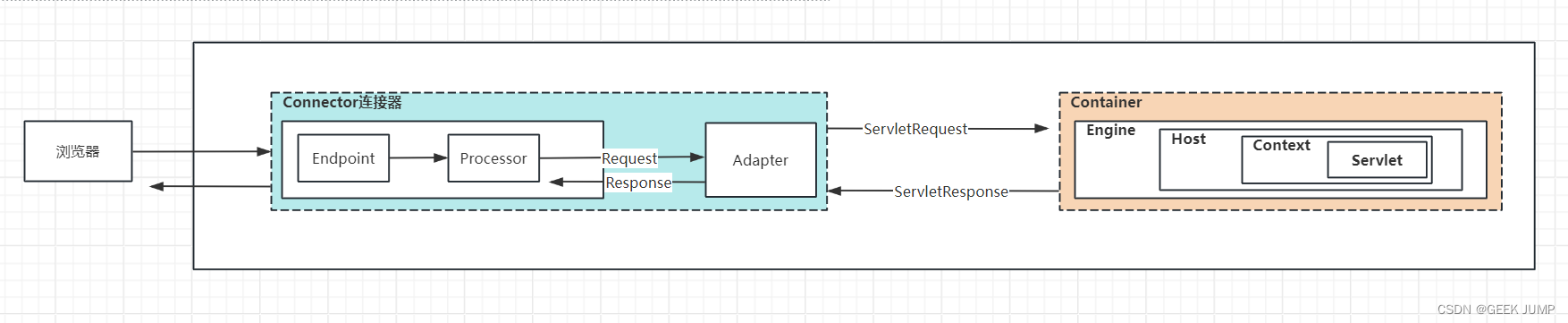
Tomcat组件架构与数据流
一、背景与简介 Tomcat我们都知道是一个开源的、实现了大部分Java EE、Servlet、JSP规范的Servlet容器, 允许我们将实现了Serlvet接口的Web程序war包进行部署运行。 但是你有对Tomcat做过细致的学习么? 我相信大部分同学和我一样,之前也是只会进行简单使用&#x…...

AES算法:数据传输的安全保障
在当今数字化时代,数据安全成为了一个非常重要的问题。随着互联网的普及和信息技术的发展,我们需要一种可靠的加密算法来保护我们的敏感数据。Advanced Encryption Standard(AES)算法应运而生。本文将介绍AES算法的优缺点、解决了…...

前端小案例——动态导航栏文字(HTML + CSS, 附源码)
一、前言 实现功能: 这案例是一个具有动态效果的导航栏。导航栏的样式设置了一个灰色的背景,并使用flex布局在水平方向上平均分配了四个选项。每个选项都是一个li元素,包含一个文本和一个横向的下划线。 当鼠标悬停在选项上时,选项的文本颜色…...
【2024-02-04】)
前置机、堡垒机(跳板机)【2024-02-04】
文章目录 0、前言1、前置机1.1、概念1.2、功能1.3、使用场景1.4、总结 2、堡垒机2.1、概念2.2、功能2.3、使用场景2.4、总结 3、前置机和堡垒机3.1、设计理念与目的3.2、功能3.3、使用场景 0、前言 文章借鉴: https://blog.csdn.net/weixin_45565886/article/detai…...

从编程中理解:大脑的短期记忆和长期记忆
在编程中,我们可以将大脑的短期记忆和长期记忆类比为程序中的变量作用域和持久化存储。在Unity C#编程环境下,可以这样解释: 假设金庸武侠世界中的人物张无忌正在修炼九阳真经。我们用C#代码来模拟他学习武功的过程,其中涉及的“…...
Rust 本地文档的使用:rustup doc
Rust 是一种系统级编程语言,以其安全性、速度和内存控制能力而闻名。为了方便开发者更好地了解并利用 Rust 标准库和工具链中的功能,Rust 提供了一种内置的文档浏览方式——通过 rustup doc 命令。 安装 rustup 在查阅 Rust 文档之前,确保你…...
)
uni-app切换页面刷新,返回上一页刷新(onShow钩子函数的使用)
切换页面刷新:通过onShow()便可实现 返回上一页通过uni.navigateBack({delta: 1});实现 以返回上一页刷新为例 从B页面返回上一页到A页面,在A页面写入方法refreshHandler() //a.vue methods: { // 执行刷新逻辑refreshHandler() {uni.request({ur…...
adb 无线连接 操作Android设备
最近集五福活动比较热门 可以用这个工具 用自己擅长的语言写一个循环程序 运行起来就可以 自动帮我们 看视频得福卡了 很方便 while (true) {sleep(mt_rand(15, 25));system(adb shell input swipe 500 2000 500 1000 100); } 1. 首先下载 安卓开发工具 adb adb网盘链接 链接…...

春节运维不打烊:一体化运维高效保障企业IT与机房环境
随着技术的不断发展和企业数字化转型的深入,IT运维已经成为企业运营不可或缺的一部分。尤其在春节期间,一体化运维管理系统以其独特的技术特性和卓越的功能,为企业的稳定运行提供了坚实保障,确保了节日的祥和与工作的连续高效。 一…...

类银河恶魔城学习记录1-5 CollisionCheck源代码 P32
Alex教程每一P的教程原代码加上我自己的理解初步理解写的注释,可供学习Alex教程的人参考 【Unity教程】从0编程制作类银河恶魔城游戏_哔哩哔哩_bilibili Player.cs using System.Collections; using System.Collections.Generic; using Unity.VisualScripting; u…...

spring boot 使用 Kafka
一、Kafka作为消息队列的好处 高吞吐量:Kafka能够处理大规模的数据流,并支持高吞吐量的消息传输。 持久性:Kafka将消息持久化到磁盘上,保证了消息不会因为系统故障而丢失。 分布式:Kafka是一个分布式系统,…...
LFU缓存(Leetcode460)
例题: 分析: 这道题可以用两个哈希表来实现,一个hash表(kvMap)用来存储节点,另一个hash表(freqMap)用来存储双向链表,链表的头节点代表最近使用的元素,离头节…...

Vue学习笔记:计算属性
计算属性 入门进阶二次进阶三次进阶四次进阶结界五次进阶六次进阶七次进阶八次进阶九次进阶终章彩蛋 入门 Vue.js中,计算属性示例: export default {data() {return {firstName: John,lastName: Doe};},computed: {// 计算属性:全名fullNam…...

深度学习本科课程 实验2 前馈神经网络
任务 3.3 课程实验要求 (1)手动实现前馈神经网络解决上述回归、二分类、多分类任务 l 从训练时间、预测精度、Loss变化等角度分析实验结果(最好使用图表展示) (2)利用torch.nn实现前馈神经网络解决上述回归…...
【python】python爱心代码【附源码】
一、实现效果: 欢迎来到英杰社区https://bbs.csdn.net/topics/617804998 二、完整代码: import math import random import threading import time from math import sin, cos, pi, log from tkinter import * import re# 烟花相关设置 Fireworks [] m…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...
