PAT-Apat甲级题1007(python和c++实现)
PTA | 1007 Maximum Subsequence Sum
1007 Maximum Subsequence Sum
作者 CHEN, Yue
单位 浙江大学
Given a sequence of K integers { N1, N2, ..., NK }. A continuous subsequence is defined to be { Ni, Ni+1, ..., Nj } where 1≤i≤j≤K. The Maximum Subsequence is the continuous subsequence which has the largest sum of its elements. For example, given sequence { -2, 11, -4, 13, -5, -2 }, its maximum subsequence is { 11, -4, 13 } with the largest sum being 20.
Now you are supposed to find the largest sum, together with the first and the last numbers of the maximum subsequence.
Input Specification:
Each input file contains one test case. Each case occupies two lines. The first line contains a positive integer K (≤10000). The second line contains K numbers, separated by a space.
Output Specification:
For each test case, output in one line the largest sum, together with the first and the last numbers of the maximum subsequence. The numbers must be separated by one space, but there must be no extra space at the end of a line. In case that the maximum subsequence is not unique, output the one with the smallest indices i and j (as shown by the sample case). If all the K numbers are negative, then its maximum sum is defined to be 0, and you are supposed to output the first and the last numbers of the whole sequence.
Sample Input:
10
-10 1 2 3 4 -5 -23 3 7 -21
Sample Output:
10 1 4万事开头难,先读题!
给定K个整数{ N1,N2,...,NK }。连续子序列被定义为{ Ni,Ni+1,...,其中1≤i≤j≤K。最大子序列(Maximum Subsequence)是一个连续的子序列,它具有最大的元素和。例如,给定序列{-2,11,-4,13,-5,-2 },其最大子序列为{ 11,-4,13 },最大和为20。
现在你应该找到最大的总和,以及最大子序列的第一个和最后一个数字。
输入规范:
每个输入文件包含一个测试用例。每种情况占两行。第一行包含正整数K(≤10000)。第二行包含K个数字,由空格分隔。
输出规格:
对于每个测试用例,在一行中输出最大和,以及最大子序列的第一个和最后一个数字。数字之间必须用一个空格隔开,但行尾不能有多余的空格。如果最大子序列不是唯一的,则输出具有最小索引i和j的子序列(如示例所示)。如果所有的K数都是负数,那么它的最大和被定义为0,你应该输出整个序列的第一个和最后一个数字。
由题目可以提取到以下关键信息:
1, 给出指定长度的数组,一行输入长度,一行输入数组,最大长度是10000
2, 要求的结果是:最大连续子数组的和以及这段子数组的起始位置和末尾位置,考虑是差分和前缀和的应用
3, 如果是全负数数组,需要按照规定的输出规范进行输出
题目分析完之后,现在是手搓代码时间!!!
本题要求很简洁明了,即求最大的连续子数组和,在这里考虑使用差分与前缀和的思想对本题进行求解,同时又需要输出这段子数组的起始位置和末尾位置,因此首先定义两个变量用于记录这两个位置:head和tail,对输入数据进行处理,定义k用于接收数组的长度,对于C++,可以考虑定义长度为10001的数组用于存储,python的列表没有长度限制,因此只需要定于列表生成式对输入进行处理即可。
由于考虑使用差分和前缀和的思想解决本题,因此这里为了方便后续操作,分别对输入数组的下标0位置和前缀和数组的下标为零位置赋初值:0,使得前缀和数组中自下标位置起为“前 [i] 个子数组的和”,至于输入数组赋初值的原因,则是为了配合前缀和数组方便操作。
初始化代码和对于输入的处理部分如下:
python部分:
k = int(input()) # 接收输入
lst = [int(i) for i in input().split()] # 接收输入数组
lst.insert(0,0) # 输入数组下标为0位置赋初值0
sum_ = [0] * (len(lst)+1) # 生成前缀和数组,为了防止索引越界,一般考虑稍微初始化大一点点
for i in range(1, len(lst)):sum_[i] = sum_[i-1] + lst[i] # 计算前缀和数组C++部分:
cin >> k;// 接收输入sum_[0] = 0; // 前缀和数组初始值赋0for(int i=1;i<=k; i++){cin>> arr[i]; // 接收输入数组}for(int i=1; i<= k; i++){sum_[i] = sum_[i-1] + arr[i]; // 计算前缀和数组}接下来是本题解题的核心部分,根据前缀和数组计算连续数组的最大和部分。
由于初始化前缀和数组第一个元素为0,这里则直接从下标为1的位置开始操作,首先定义用于记录最大和的变量result,初始化为-1,这里因为全负数数组有规定的输出格式,且不需要其他额外的操作,因此为了遍历完前缀和数组后可以分辨出该数组是否为全负数数组,此处初始化为-1而不是0,因为全负数数组其子序列的和不可能为正数,但非全负数数组可能存在全零的情况,故此处不初始化为0,避免对后续造成干扰,细节处应该给予充分考虑,避免造成不必要的代码调试时间的浪费。
此后,我们使用循环,遍历前缀和数组,初始化一个标记变量lowest,用于记录每次最长子数组发生变化后的起始部分,这里初始化为0,因为0下标对应的元素初始化为0,不纳入考虑,循环遍历时,应当使用前缀和数组的元素对下标为lowest的前缀和数组元素进行相减,比如:对于下标为i的前缀和数组sum[i],与标记位置元素sum[lowest] ,其差值为自下标lowest+1到下标为i这段子数组的和,得到这部分子数组的和,我们可以将其与result进行比较,只要发现结果大于result,则更新result,同时head更新为lowest+1,tail更新为i,即【head , tail】部分即为当前所遍历得到的最大连续子数组和,通过循环不断更新i的位置,最终将得到最大的连续子数组和result,以及其初始位置和结束位置下标,同时需要注意的是:标记lowest并不是一成不变的,需要在每次遍历的时候比较sum[i]以及sum[lowest]的大小,只要sum[i]比sum[lowest]小,则更新lowest的位置为i,这里也不难理解,当被减数sum[i]一定时,只有减数sum[lowest]最小,得到的差才能最大,也就是下标为lowest+1到i这部分子数组的和才能最大,这也是解决连续子数组问题的关键点之一。以下是这部分的代码实现:
python:
res = -1 # 最大连续子数组和
lowest = 0 # 标记位置
head = 0
tail = 0
for end in range(len(lst)):if sum_[end] - sum_[lowest] > res: # 当前计算结果大于之前计算得到的最大连续子数组和,更新res = sum_[end] - sum_[lowest]head = lowest + 1tail = endif sum_[lowest] > sum_[end]: # 保证减数最小lowest = endC++:
// 初始化对应变量
int lowest=0,result=-1;
int head,tail;for(int end=1; end<=k; end ++){if(sum_[end] - sum_[lowest] > result){ // 当前计算得到的最大连续子数组和大于以前计算的result = sum_[end] - sum_[lowest];head = arr[lowest + 1];tail = arr[end];}if(sum_[lowest] > sum_[end]){ // 保证减数最小lowest = end;}
}最后是完整的的代码部分:
C++:
#include<bits/stdc++.h>
using namespace std;int k;
int lowest=0,result=-1;
int head,tail;
int arr[1001],sum_[1001];int main(){cin >> k;// 接收输入sum_[0] = 0; // 前缀和数组初始值赋0for(int i=1;i<=k; i++){cin>> arr[i]; // 接收输入数组}for(int i=1; i<= k; i++){sum_[i] = sum_[i-1] + arr[i]; // 计算前缀和数组}for(int end=1; end<=k; end ++){if(sum_[end] - sum_[lowest] > result){result = sum_[end] - sum_[lowest];head = arr[lowest + 1];tail = arr[end];}if(sum_[lowest] > sum_[end]){lowest = end;}}if(result < 0){cout << 0 << " " << arr[1] << " " << arr[k];}else{cout << result << " " << head <<" " << tail;}
}python:
k = int(input()) # 接收输入
lst = [int(i) for i in input().split()] # 接收输入数组
lst.insert(0,0) # 输入数组下标为0位置赋初值0
sum_ = [0] * (len(lst)+1) # 生成前缀和数组,为了防止索引越界,一般考虑稍微初始化大一点点
for i in range(1, len(lst)):sum_[i] = sum_[i-1] + lst[i] # 计算前缀和数组
res = -1
lowest = 0
head = 0
tail = 0
for end in range(len(lst)):if sum_[end] - sum_[lowest] > res:res = sum_[end] - sum_[lowest]head = lowest + 1tail = endif sum_[lowest] > sum_[end]:lowest = endif res < 0:print("0" + " " + str(lst[1]) + " " + str(lst[k]))
else:print(str(res) + " " + str(head) + " " + str(tail))最后附上AK截图:
python

C++:

写在后面:
本题题眼在于“最大连续子数组和”,一般此类题目的解题思路都在于“差分与前缀和”这块,构建前缀和数组,通过“被减数一定,减数最小,差值(最大连续子数组和)最大”思路来进行解题,本题难度适中,核心部分可以当作模板记忆。
以上就是本题的全部内容,主要在于差分与前缀和思想的应用,对此还不清楚的童鞋可以去详细学习,当然如果您有需要,我可以出一期对于差分与前缀和讲解的文章或视频,您可以评论区留言,如果对于以上内容您有什么意见或建议,欢迎评论区交流!
相关文章:

PAT-Apat甲级题1007(python和c++实现)
PTA | 1007 Maximum Subsequence Sum 1007 Maximum Subsequence Sum 作者 CHEN, Yue 单位 浙江大学 Given a sequence of K integers { N1, N2, ..., NK }. A continuous subsequence is defined to be { Ni, Ni1, ..., Nj } where 1≤i≤j≤K. The Maximum Su…...

洛谷:P2957 [USACO09OCT] Barn Echoes G
题目描述 The cows enjoy mooing at the barn because their moos echo back, although sometimes not completely. Bessie, ever the excellent secretary, has been recording the exact wording of the moo as it goes out and returns. She is curious as to just how mu…...

flinksqlbug : AggregateFunction udf Could not extract a data type from
org.apache.flink.table.api.ValidationException: SQL validation failed. An error occurred in the type inference logic of function ‘default_catalog.default_database.CollectSetSort’. org.apache.flink.table.api.ValidationException: An error occurred in the t…...

Aigtek高压放大器用途是什么呢
高压放大器在电子领域中扮演着至关重要的角色,其主要作用是将低电压信号放大到更高的电压水平。这种类型的放大器广泛用于各种应用中,以下是高压放大器的用途以及其关键作用的详细介绍。 1、科学研究和实验室应用: 高压放大器在科学研究和实验…...
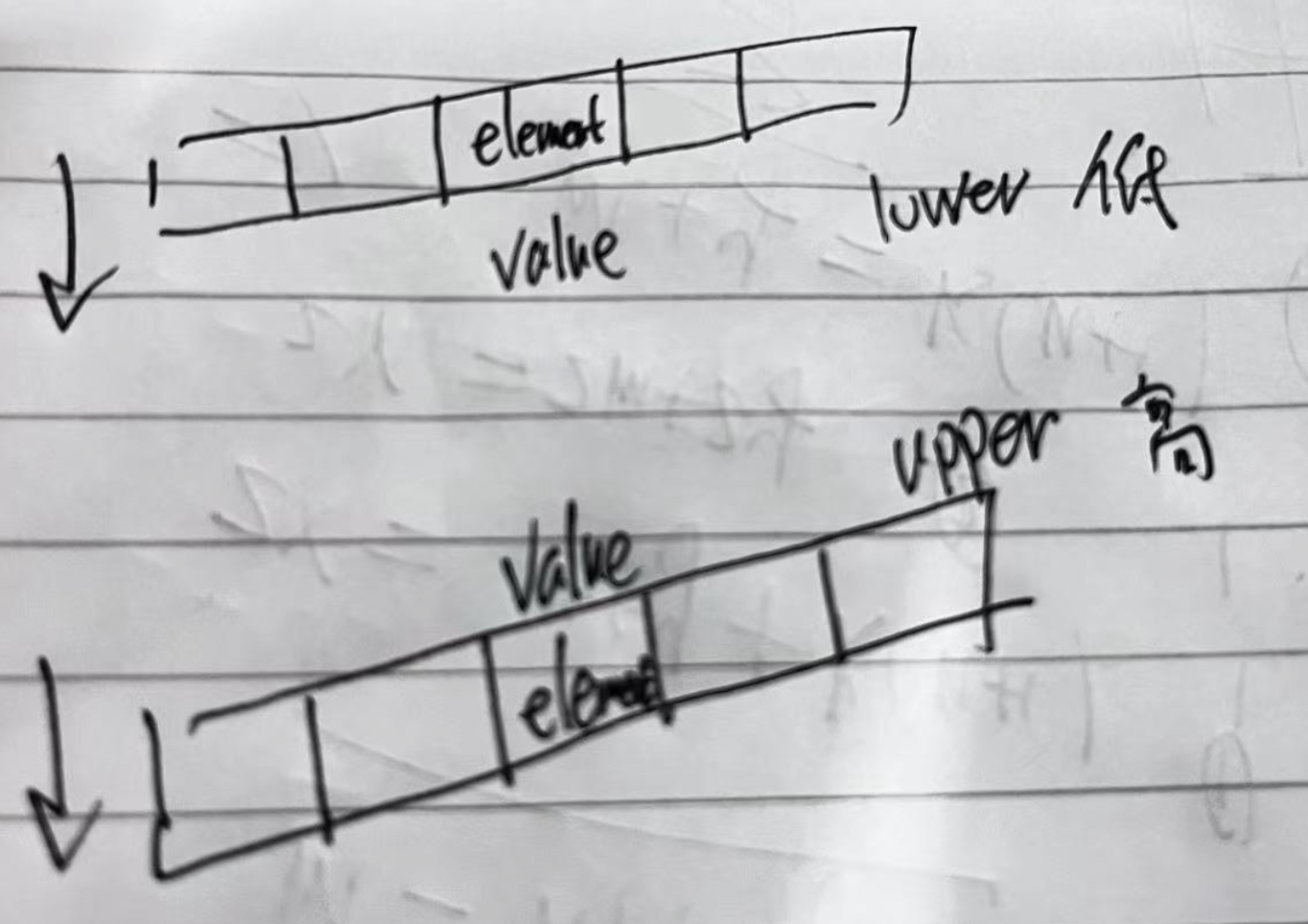
c++ STL less 的视角
c less 函数在不同的地方感觉所起的作用是不一样的, 这中间原因是 less 的视角不一样, 下面尝试给出解释下, 方便记忆 1、 左右视角 符合 排序sort less(value, element) less 表示一种 “符合关系“, 表示sort 后…...
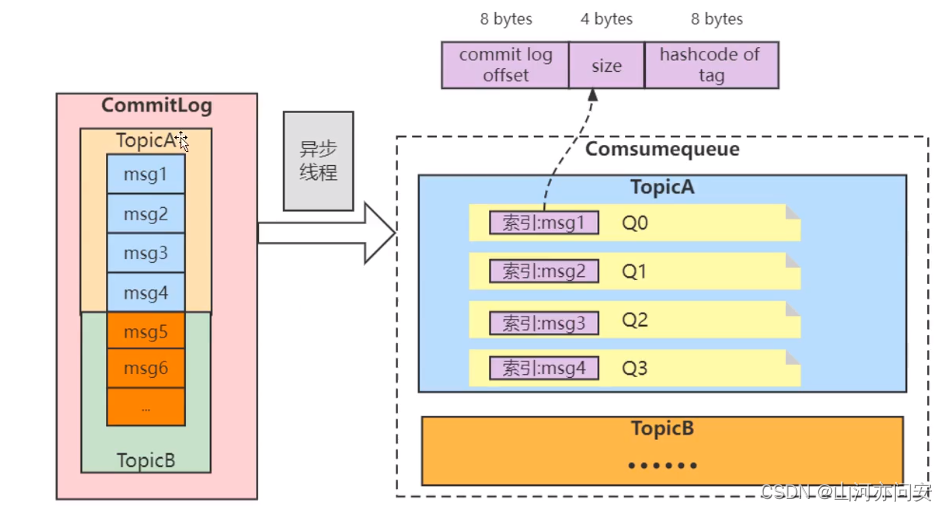
MQ面试题整理(持续更新)
1. MQ的优缺点 优点:解耦,异步,削峰 缺点: 系统可用性降低 系统引入的外部依赖越多,越容易挂掉。万一 MQ 挂了,MQ 一挂,整套系统崩 溃,你不就完了?系统复杂度提高 硬生…...

2401cmake,学习cmake2
步4:安装与测试 现在开始给项目添加安装规则和支持测试. 安装规则 安装规则非常简单:对MathFunctions,想安装库和头文件,对应用,想安装可执行文件和配置头. 所以在MathFunctions/CMakeLists.txt尾添加: install(TARGETS MathFunctions DESTINATION lib) install(FILES Mat…...

理解Jetpack Compose中的`remember`和`mutableStateOf`
理解Jetpack Compose中的remember和mutableStateOf 在现代Android开发中,Jetpack Compose已经成为构建原生UI的首选工具。它引入了一种声明式的编程模式,极大地简化了UI开发。在Compose的世界里,remember和mutableStateOf是两个非常关键的函…...

3D力导向树插件-3d-force-graph学习002
一、实现效果:节点文字同时展示 节点显示不同颜色节点盒label文字并存节点上添加点击事件 二、利用插件:CSS2DRenderer 提示:以下引入文件均可在安装完3d-force-graph的安装包里找到 三、关键代码 提示:模拟数据可按如下格式填…...
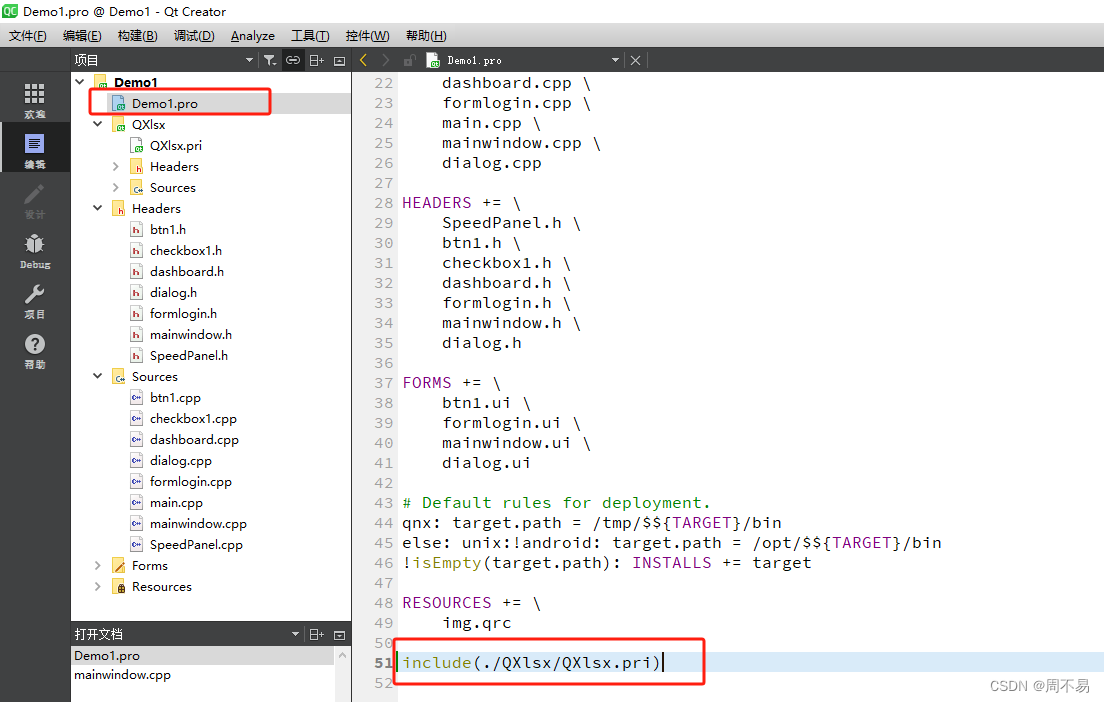
QXlsx Qt操作excel
QXlsx 是一个用于处理Excel文件的开源C库。它允许你在你的C应用程序中读取和写入Microsoft Excel文件(.xlsx格式)。该库支持多种操作,包括创建新的工作簿、读取和写入单元格数据、格式化单元格、以及其他与Excel文件相关的功能。 支持跨平台…...

Node.js 包管理工具
一、概念介绍 1.1 包是什么 『包』英文单词是 package ,代表了一组特定功能的源码集合 1.2 包管理工具 管理『包』的应用软件,可以对「包」进行 下载安装 , 更新 , 删除 , 上传 等操作。 借助包管理工具࿰…...
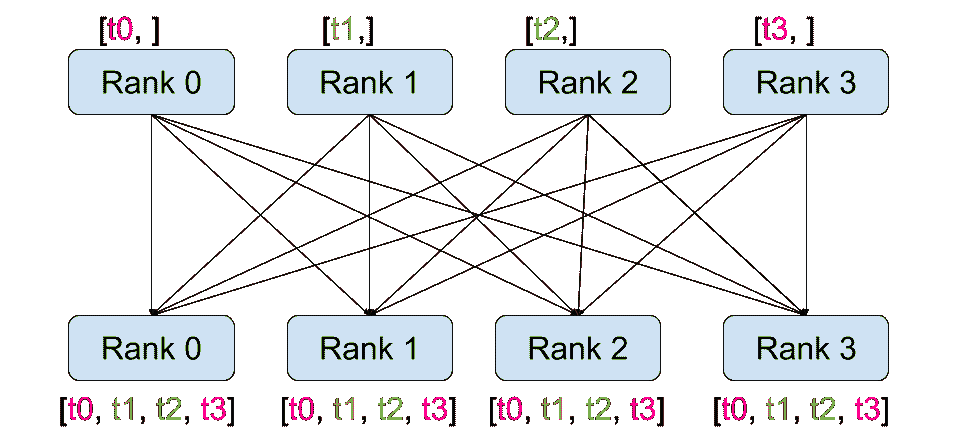
PyTorch 2.2 中文官方教程(十七)
(Beta)使用缩放点积注意力(SDPA)实现高性能 Transformer 原文:pytorch.org/tutorials/intermediate/scaled_dot_product_attention_tutorial.html 译者:飞龙 协议:CC BY-NC-SA 4.0 注意 点击这…...

Failed at the chromedriver@2.27.2 install script.
目录 【错误描述】Failed at the chromedriver2.27.2 install script. npm install报的错误 【解决方法】 删除node_modules文件夹npm install chromedriver --chromedriver_cdnurlhttp://cdn.npm.taobao.org/dist/chromedrivernpm install 【未解决】 下载该zip包运行这个&…...
OpenResty 安装
安装OpenResty 1.安装 首先你的Linux虚拟机必须联网 1)安装开发库 首先要安装OpenResty的依赖开发库,执行命令: yum install -y pcre-devel openssl-devel gcc --skip-broken2)安装OpenResty仓库 你可以在你的 CentOS 系统中…...
套路化编程 C# winform 自适应缩放布局
本例程实现基本的自适应缩放布局。 在本例程中你将会学习到如何通过鼠标改变界面比例(SplitContainer)、如何使用流布局(FlowLayoutPanel)排列控件,当然首先需要了解如何设置控件随窗口缩放。 目录 创建项目 编辑…...
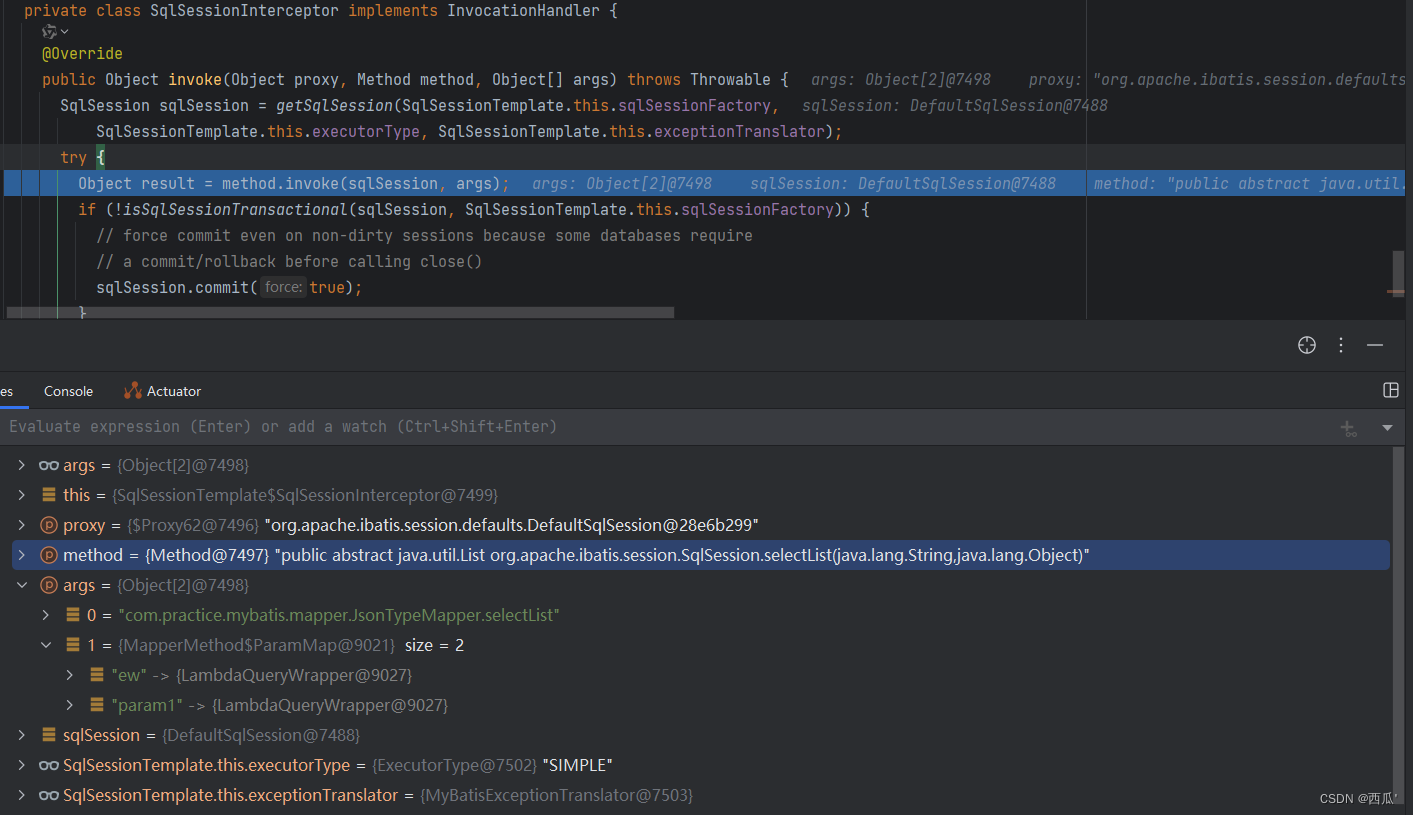
源码梳理(3)MybatisPlus启动流程
文章目录 1,MybatisPlus的使用示例2,BaseMapper方法的执行2,1 MybatisMapperProxy代理对象2.2 InvocationHandler接口(JDK动态代理)2.3 MapperMethodInvoker接口2.4 MybatisMapperMethod 3,SqlSession的执行流程3.1 Sq…...
《学成在线》微服务实战项目实操笔记系列(P1~P49)【上】
《学成在线》项目实操笔记系列【上】,跟视频的每一P对应,全系列12万字,涵盖详细步骤与问题的解决方案。如果你操作到某一步卡壳,参考这篇,相信会带给你极大启发。同时也欢迎大家提问与讨论,我会尽力帮大家解…...
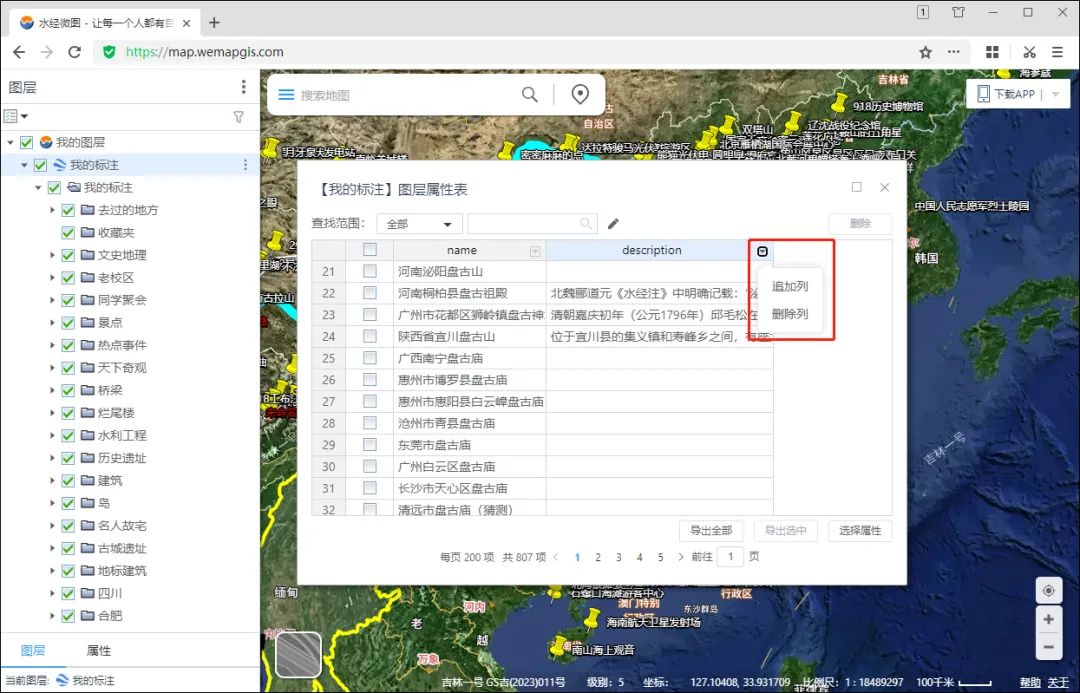
两种添加删除属性字段的方法
水经微图(简称“微图”)中的图层均有属性字段,无论是复合图层,还是点线面图层的字段都可以根据实际情况进行添加或删除。 这里,就为你分享两种添加删除字段的方法。 添加删除字段方法一 当需要添加删除图层的属性字…...

ObjectMapper之处理JSON序列化和反序列化
目录 基本示例Java 对象转 JSON 字符串(序列化)JSON 字符串转 Java 对象(反序列化) 高级特性忽略未知属性使用注解自定义序列化 当然可以。让我们通过更详细的例子来探索 ObjectMapper 的使用,包括基本的序列化和反序…...
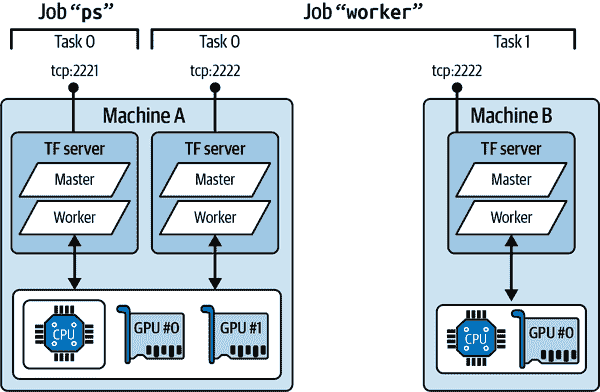
Sklearn、TensorFlow 与 Keras 机器学习实用指南第三版(八)
原文:Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow 译者:飞龙 协议:CC BY-NC-SA 4.0 第十八章:强化学习 强化学习(RL)是当今最激动人心的机器学习领域之一,也是最古老…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
