让IIS支持SSE (Server Sent Events)
本文只探讨IIS+Python网站的情况,对于asp.net也应该不用这么麻烦。
先上结论:用反向代理: IIS + URL Rewrite + waitress
Waitress是一个纯python编写独立的WSGI服务器,功能比Gunicorn弱一些,但可以运行在windows平台上(Gunicorn 和 uwsgi 不支持windows)。
背景:用django做了个实时监控脚本执行状态的页面。里面用到了SSE技术,在开发环境一切正常,任务脚本执行过程中每个状态输出,web服务器端都会产生一个response推送给客户端,在浏览器中跨域实时看到任务执行状态。但部署到IIS中,web服务器会等全部任务执行完毕,才一次性把中间过程所有状态输出合并成一个response推送给客户端,界面卡住不动,无法实时看到当前状态。
折腾过程:
1、先是尝试了IIS禁用缓存、禁用动态内容压缩,问题依旧。
2、推断可能是wfastcgi导致的,问遍百度谷歌gpt都找不到禁用wfastcgi的buffer的方法
3、巨硬说部署django可以用HTTPPlatformHandler替代wfastcgi,于是折腾HTTPPlatformHandler,发现对于部署django网站HTTPPlatformHandler似乎真的比wfastcgi要简单呢!但无奈HTTPPlatformHandler还是解决不了禁用buffer的问题,并且github上HTTPPlatformHandler的开发者说v1.2确实有这个问题,但v1.2已经是最终版本,HTTPPlatformHandler会迁移到ASP.NET Core去。然后stackoverflow上有人说确实用ASP.NET Core解决了这个问题。
4、接着折腾ASP.NET Core,发现ASP.NET Core+python的部署指引在网上根本找不到。本来尝试肯一下ASP.NET Core的文档的,啃了一轮最后还是放弃了。
5、最终完全放弃IIS了,直接重新买个轻量云装linux,去折腾Nginx+uwsgi+django了,比较顺利地解决了SSE问题了。
6、但对IIS上部署还是有点不死心,于是又继续追着谷歌和gpt折腾这个问题,最后gpt建议试一下IIS反向代理,一试,居然成功了!而且配置并不复杂。嘛的此前折腾死我了!
下面是一个简单的步骤指南来配置IIS作为反向代理:
步骤 1: 安装 IIS 和必要的模块
- 确保安装了IIS。
- 安装URL Rewrite模块,这是一个IIS扩展,提供了URL重写功能。
- 安装Application Request Routing (ARR),ARR是一个IIS扩展,提供了代理功能。
步骤 2: 配置 Application Request Routing
- 打开IIS管理器。
- 选择服务器名称,在“应用程序请求路由缓存”下,打开“服务器代理设置”。
- 勾选“启用代理”,然后应用更改。
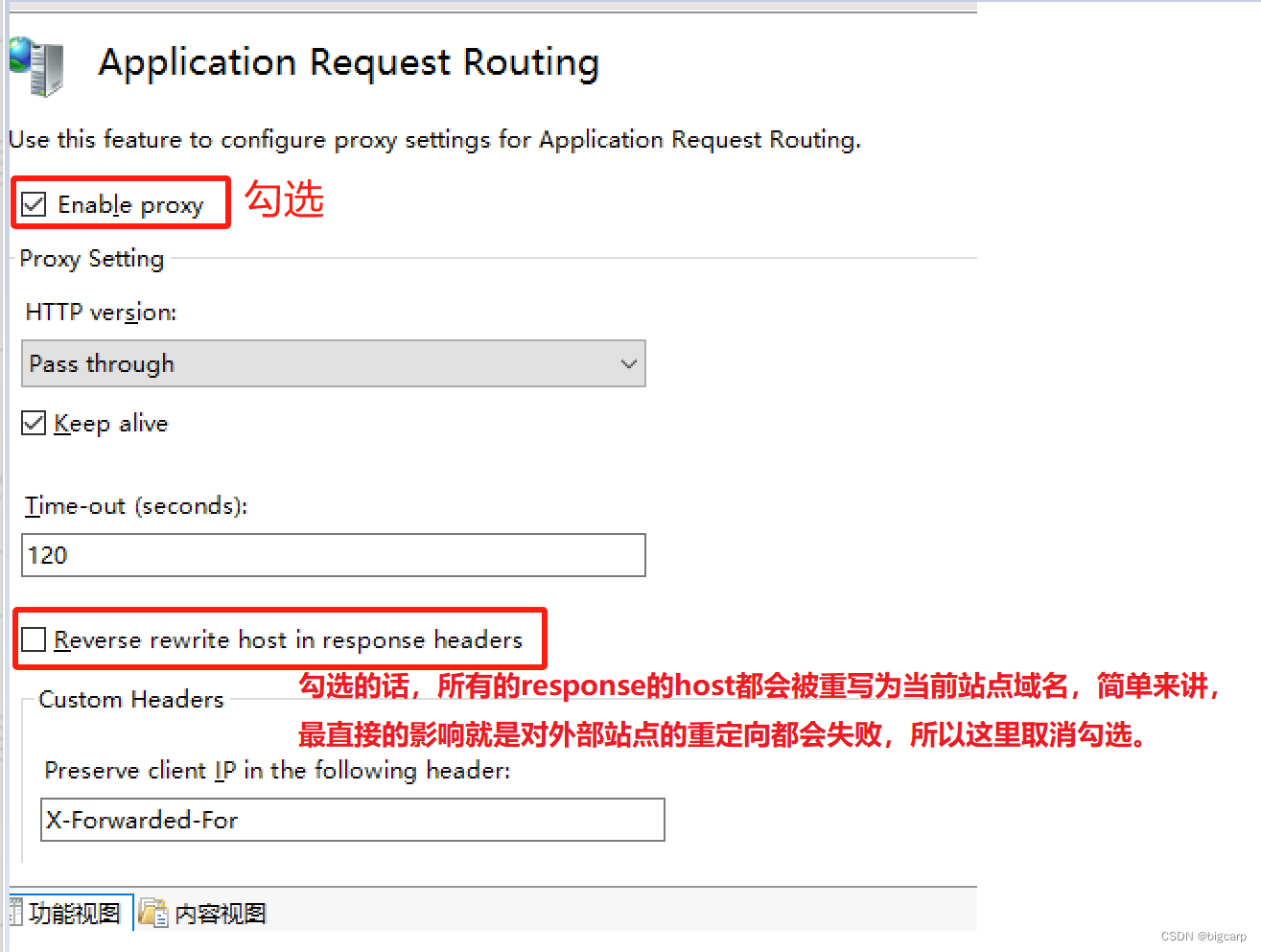
步骤 3: 配置web.config
<configuration><system.webServer><rewrite><rules><rule name="ReverseProxyInboundRule1" stopProcessing="true"><match url="(.*)" /><action type="Rewrite" url="http://127.0.0.1:8001/{R:1}" /></rule></rules></rewrite></system.webServer>
</configuration>
这个配置假设你的Django应用程序正在监听127.0.0.1的8001端口。所有到达IIS的请求将被重写(转发)到这个地址。
在windows系统上怎么启动waitress 我就不写了,网上有很多。备注一下,通过python runserver.py 方式启动waitress的代码如下:
# runserver.pyfrom waitress import serve
from xxxxxx.wsgi import application #xxxxxx.wsgi 中的xxx是自己项目目录名serve(app=application,host='127.0.0.1', # 如果不用反向代理,直接让waitress对外提供服务,这里就填0.0.0.0,端口填80port=8001
)
如果通过exe文件启动waitress的命令是:
# 须在虚拟环境下执行,
# ip:port 写0.0.0.0:80 还是写127.0.0.1:8000 请根据实际情况改
# xxxxx.wsgi 中的xxxx是wsgi.py 所在目录,这个文件夹名一般与项目名同名path\to\waitress-serve.exe --listen=127.0.0.1:8001 xxxxx.wsgi:application# 这条命令跟runserver.py中每一句的对应关系可以大致着样理解:
# waitress-serve.exe 中的 waitress 对应 from waitress
# waitress-serve.exe 中的 serve 对应 import serve
# listen=127.0.0.1:8001 对应host='127.0.0.1',port=8091
# xxxxx.wsgi 对应 from xxxxx.wsgi
# application 对应 import application如果折腾ASP.NET Core来部署的话,这条命令可能用得上。
相关文章:

让IIS支持SSE (Server Sent Events)
本文只探讨IISPython网站的情况,对于asp.net也应该不用这么麻烦。 先上结论:用反向代理: IIS URL Rewrite waitress Waitress是一个纯python编写独立的WSGI服务器,功能比Gunicorn弱一些,但可以运行在windows平台上&…...

新手从零开始学习数学建模论文写作(美赛论文临时抱佛脚篇)
本文记录于数学建模老哥视频的学习过程中。b站视频:http://【【零基础教程】老哥:数学建模算法、编程、写作和获奖指南全流程培训!】https://www.bilibili.com/video/BV1kC4y1a7Ee?p50&vd_sourceff53a726c62f94eda5f615bd4a62c458 目录…...

k8s存储之PV、PVC
在k8s集群中,资源存储会散落到各个工作节点上,这样对用资源调用很不方便,那么k8s是如何实现存储资源共享的呢,本文浅尝辄止的探讨一下,k8s是通过pv、pvc实现的。 一、PV、PVC的概念 1、持久卷(PV) pv是Pe…...

go-基于逃逸分析来提升性能程序
go-基于逃逸分析来提升性能程序 为什么要学习逃逸分析: 为了提高程序的性能,通过逃逸分析我们能知道指标是分配到堆上还是栈上,如何是 分配到栈上,内存的分配和释放都是由编译器进行管理的,分配和释放的速度都非常的…...
[软件工具]文档页数统计工具软件pdf统计页数word统计页数ppt统计页数图文打印店快速报价工具
文档页数统计工具软件——打印方面好帮手 在信息化时代,文档已成为我们工作、学习、生活中不可或缺的一部分。无论是学术论文、商业报告,还是个人日记,都需要我们对其进行有效的管理。而在这个过程中,文档页数统计工具软件就显得…...

linux编译ffmpeg动态库
1,获取源码:git clone https://git.ffmpeg.org/ffmpeg.git 2,创建编译目录,并编译、安装, cd ffmpeg mkdir build cd build ../configure --prefix~/ffmpeg --enable-shared --enable-debug1 //configure后需要使…...

Unity3d Cinemachine篇(完)— TargetGroup
文章目录 前言使用TargetGroup追随多个模型1. 创建二个游戏物体2. 创建TargetGroup相机3. 设置相机4. 完成 前言 上一期我们简单的使用了ClearShot相机,这次我们来使用一下TargetGroup 使用TargetGroup追随多个模型 1. 创建二个游戏物体 2. 创建TargetGroup相机 3…...

事件驱动架构:使用Flask实现MinIO事件通知Webhooks
MinIO的事件通知可能一开始看起来并不激动人心,但一旦掌握了它们的力量,它们就能照亮您存储桶内的动态。事件通知是一个全面、高效的对象存储系统中的关键组件。Webhooks是我个人最喜欢的工具,用于与MinIO集成。它们在事件的世界中就像一把瑞…...

力扣面试150 只出现一次的数字Ⅱ 哈希 统计数位 DFA有穷自动机
Problem: 137. 只出现一次的数字 II 文章目录 思路💖 哈希💖 位数统计💖 DFA 状态机 思路 👨🏫 参考 💖 哈希 ⏰ 时间复杂度: O ( n ) O(n) O(n) 🌎 空间复杂度: O ( n ) O(n) O(n) cl…...
R语言学习case10:ggplot基础画图Parallel Coordinate Plot 平行坐标图
step1: 导入ggplot2库文件 library(ggplot2)step2:带入自带的iris数据集 iris <- datasets::irisstep3:查看数据信息 dim(iris)维度为 [150,5] head(iris)查看数据前6行的信息 step4:利用ggplot工具包绘图 plot5 <- ggparcoord(…...

Easy Excel动态表头的实现
步骤: 1.查找官方API文档理解实现 2.实现融入到代码里面 一:Easy Excel动态头实时生成头写入 动态头实时生成头写入 二:实现 目的:实现表头为,第一列是固定列,第二列为动态生成的时间段的每一天的日期…...
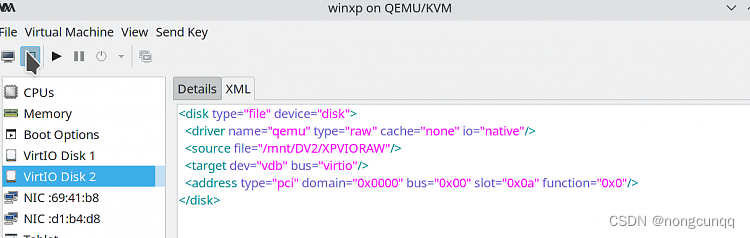
kvm qemu 优化 windows 虚拟机速度
主要优化磁盘 io 和网络 io 都选为 virtio windows 驱动下载 https://fedorapeople.org/groups/virt/virtio-win/direct-downloads/archive-virtio/virtio-win-0.1.185-2/virtio-win-0.1.185.iso I also had incredibly slow performance with my virtual HDD. The followin…...
银行数据仓库体系实践(18)--数据应用之信用风险建模
信用风险 银行的经营风险的机构,那在第15节也提到了巴塞尔新资本协议对于银行风险的计量和监管要求,其中信用风险是银行经营的主要风险之一,它的管理好坏直接影响到银行的经营利润和稳定经营。信用风险是指交易对手未能履行约定契约中的义务而…...

每日一练 | 华为认证真题练习Day179
1、关于配置STUB区域需要注意的事项中描述正确的是 A. 骨干区域可以配置成为STUB区域 B. 如果将一个区域配置成为STUB区域,则该区域中的所有路由器都要配置STUB区域属性 C. STUB区域可以存在ASBR D. 虚连接可以穿越STUB 2、关于PIM-SM中的HellO报文的描述&#…...

[ubuntu]add-apt-repository 添加以及移除
add-apt-repository是一个用于添加PPA(Personal Package Archive)存储库的命令。它是Ubuntu和基于Ubuntu的Linux发行版中的apt软件包管理系统的一部分。 PPA存储库允许用户安装和更新软件包,这些软件包不包含在官方软件源中。通过添加PPA存储…...
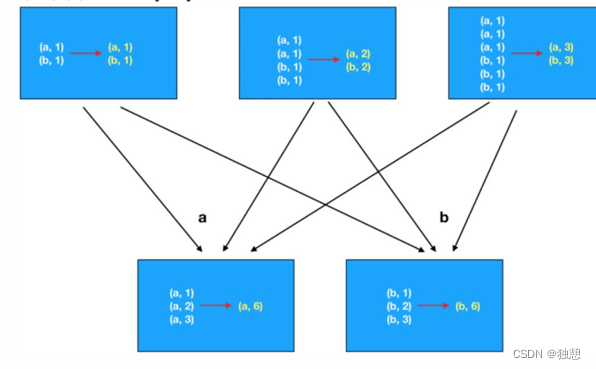
PySpark(二)RDD基础、RDD常见算子
目录 RDD RDD五大特性 RDD创建 RDD算子 常见的Transformation算子 map flatMap mapValues reduceByKey groupBy filter distinct union join intersection glom groupByKey groupByKey和reduceByKey的区别 ? sortBy sortByKey 常见的action算子 countByKey…...
修改MFC图标
摘要:本文主要讲解了MFC程序窗口图标的添加、任务栏、底部托盘的图标添加,以及所生成的exe文件图标的添加。 1、在资源视图添加Icon资源 透明图标怎么制作? 1)点击图片》右键:使用画图3D进行编辑 2&a…...
springboot158基于springboot的医院资源管理系统
简介 【毕设源码推荐 javaweb 项目】基于springbootvue 的 适用于计算机类毕业设计,课程设计参考与学习用途。仅供学习参考, 不得用于商业或者非法用途,否则,一切后果请用户自负。 看运行截图看 第五章 第四章 获取资料方式 **项…...

【算法】枚举——蓝桥杯、日期统计、特殊日期(位数之和)、2023、特殊日期(倍数)、跑步锻炼
文章目录 蓝桥杯日期统计特殊日期(位数之和)2023特殊日期(倍数)跑步锻炼 蓝桥杯 日期统计 日期统计 如果暴力枚举100个数的八次循环那就是1016次运算,时间复杂度太高了,好在前四次的2023是确定的…...
基于flask的个人博客项目从0到1
项目展示(持续完善中…) 首页 文章时间线页面 笔记页面 留言页面 关于页面 后台页面-文章管理 后台页面-笔记页面 后台页面-分类 后台管理-新增标签 后台管理-标签页面 后台管理-新增标签 后台管理-关于页面 2.项目详述 该博客开源地址点击跳转,该项目已部署上…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
