二叉树的详解

【本节目标】
- 掌握树的基本概念
- 掌握二叉树概念及特性
- 掌握二叉树的基本操作
- 完成二叉树相关的面试题练习
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看 起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:

有一个特殊的结点,称为根结点,根结点没有前驱结点

除根结点外,其余结点被分成M(M > 0)个互不相交的集合T1、T2、......、Tm,其中每一个集合 Ti (1 <= i

<= m) 又是一棵与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继树是递归定义的。



注意:树形结构中,子树之间不能有交集,否则就不是树形结构
 |
 |
结点的度:一个结点含有子树的个数称为该结点的度; 如上图:A的度为6 树的度:一棵树中,所有结点度的最大值称为树的度; 如上图:树的度为6
叶子结点或终端结点:度为0的结点称为叶结点; 如上图:B、C、H、I...等节点为叶结点
双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点; 如上图:A是B的父结点
孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点; 如上图:B是A的孩子结点根结点:一棵树中,没有双亲结点的结点;如上图:A
结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推树的高度或深度:树中结点的最大层次; 如上图:树的高度为4
树的以下概念只需了解,在看书时只要知道是什么意思即可:
非终端结点或分支结点:度不为0的结点; 如上图:D、E、F、G...等节点为分支结点兄弟结点:具有相同父结点的结点互称为兄弟结点; 如上图:B、C是兄弟结点
堂兄弟结点:双亲在同一层的结点互为堂兄弟;如上图:H、I互为兄弟结点
结点的祖先:从根到该结点所经分支上的所有结点;如上图:A是所有结点的祖先
子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图:所有结点都是A的子孙 森林:由m(m>=0)棵互不相交的树组成的集合称为森林
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,实际中树有很多种表示方式,如:双亲表示法, 孩子表示法、孩子双亲表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
 |
 |
文件系统管理(目录和文件)


一棵二叉树是结点的一个有限集合,该集合:
-
-
- 或者为空
- 或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
-
 |
从上图可以看出:
- 二叉树不存在度大于2的结点
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
注意:对于任意的二叉树都是由以下几种情况复合而成的:

大自然的奇观:

 |


若i>0,双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点 若2i+1<n,左孩子序号:2i+1,否则无左孩子

若2i+2<n,右孩子序号:2i+2,否则无右孩子
 |

二叉树的存储结构分为:顺序存储和类似于链表的链式存储。顺序存储在下节介绍。
二叉树的链式存储是通过一个一个的节点引用起来的,常见的表示方式有二叉和三叉表示方式,具体如下:
 |
孩子双亲表示法后序在平衡树位置介绍,本文采用孩子表示法来构建二叉树。
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结 构掌握还不够深入,为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习,等 二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
 |

注意:上述代码并不是创建二叉树的方式,真正创建二叉树方式后序详解重点讲解。 再看二叉树基本操作前,再回顾下二叉树的概念,二叉树是:
-
-
-
- 空树
- 非空:根节点,根节点的左子树、根节点的右子树组成的。
-
-
 |
从概念中可以看出,二叉树定义是递归式的,因此后序基本操作中基本都是按照该概念实现的。
 |
在遍历二叉树时,如果没有进行某种约定,每个人都按照自己的方式遍历,得出的结果就比较混乱,如果按 照某种规则进行约定,则每个人对于同一棵树的遍历结果肯定是相同的。如果N代表根节点,L代表根节点的 左子树,R代表根节点的右子树,则根据遍历根节点的先后次序有以下遍历方式:



NLR:前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点--->根的左子树--->根的右子树。LNR:中序遍历(Inorder Traversal)——根的左子树--->根节点--->根的右子树。LRN:后序遍历(Postorder Traversal)——根的左子树--->根的右子树--->根节点。
 |
下面主要分析前序递归遍历,中序与后序图解类似,同学们可自己动手绘制。

前序遍历结果:1 2 3 4 5 6
中序遍历结果:3 2 1 5 4 6
后序遍历结果:3 1 5 6 4 1
-
-
-
- 层序遍历
-
-
 |
【练习】请同学们根据以上二叉树的三种遍历方式,给出以下二叉树的:

相关文章:

二叉树的详解
二叉树 【本节目标】 掌握树的基本概念掌握二叉树概念及特性掌握二叉树的基本操作完成二叉树相关的面试题练习 树型结构(了解) 概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。…...

【第三十五节】idea项目的创建以及setting和Project Structure的设置
项目创建 Project Structure的设置 点击file ~ Project Structure 进入...

【c++】跟webrtc学引用计数
rtc::RefCountInterface 接口类 G:\CDN\rtcCli\m98\src\rtc_base\ref_count.h引用计数想形成一种树状结构 // Interfaces where refcounting is part of the public api should // inherit this abstract interface. The implementation of these // methods is usually provid…...
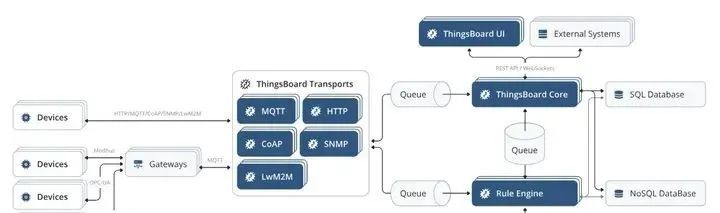
开源免费的物联网网关 IoT Gateway
1. 概述 物联网网关,也被称为IOT网关,是一种至关重要的网络设备。在物联网系统中,它承担着连接和控制各种设备的重要任务,将这些设备有效地连接到云端、本地服务器或其他设备上。它既能够在广域范围内实现互联,也能在…...

华为OD机试真题C卷-篇3
文章目录 查找一个有向网络的头节点和尾节点幼儿园篮球游戏 查找一个有向网络的头节点和尾节点 在一个有向图中,有向边用两个整数表示,第一个整数表示起始节点,第二个整数表示终止节点;图中只有一个头节点,一个或者多…...

[SWPUCTF 2021 新生赛]include
他让我们传入一个flag值 我们传入即可看到代码部分 传入一个php的伪类即可 得到经过Base64加密的flag,解密即可...
LeetCode、17. 电话号码的字母组合【中等,dfs回溯】
文章目录 前言LeetCode、17. 电话号码的字母组合【中等,dfs回溯】题目与类型思路递归回溯优化:StringBuilder来回溯补充代码:2024.1.31(简化) 资料获取 前言 博主介绍:✌目前全网粉丝2W,csdn博…...
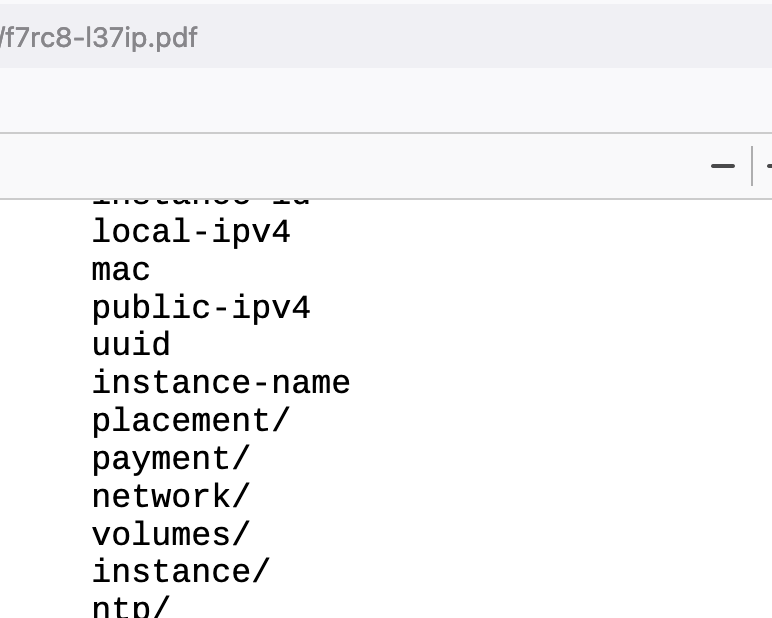
SSRF漏洞给云服务元数据带来的安全威胁
文章目录 前言元数据服务威胁1.1 Metadata元数据1.2 RAM资源管理角色1.3 STS 临时凭据利用1.4 CF云环境利用框架1.5 元数据安全性增强 TerraformGoat2.1 永久性AccessKey2.2 SSRF靶场环境搭建2.3 腾讯云CVM配角色2.4 接管腾讯云控制台 SSRF组合拳案例3.1 上传图片功能SSRF3.2 文…...

【C++】强制类型转换
强制类型转换分为显式和隐式 显式直接用小括号强制转换,float b (int)a; 隐式直接 float b 0.5; int a b; C中更推荐用四个强制类型转换的关键字: 1、static_cast, 2、const_cast, 3、reinterpret_cast, 4、dynami…...
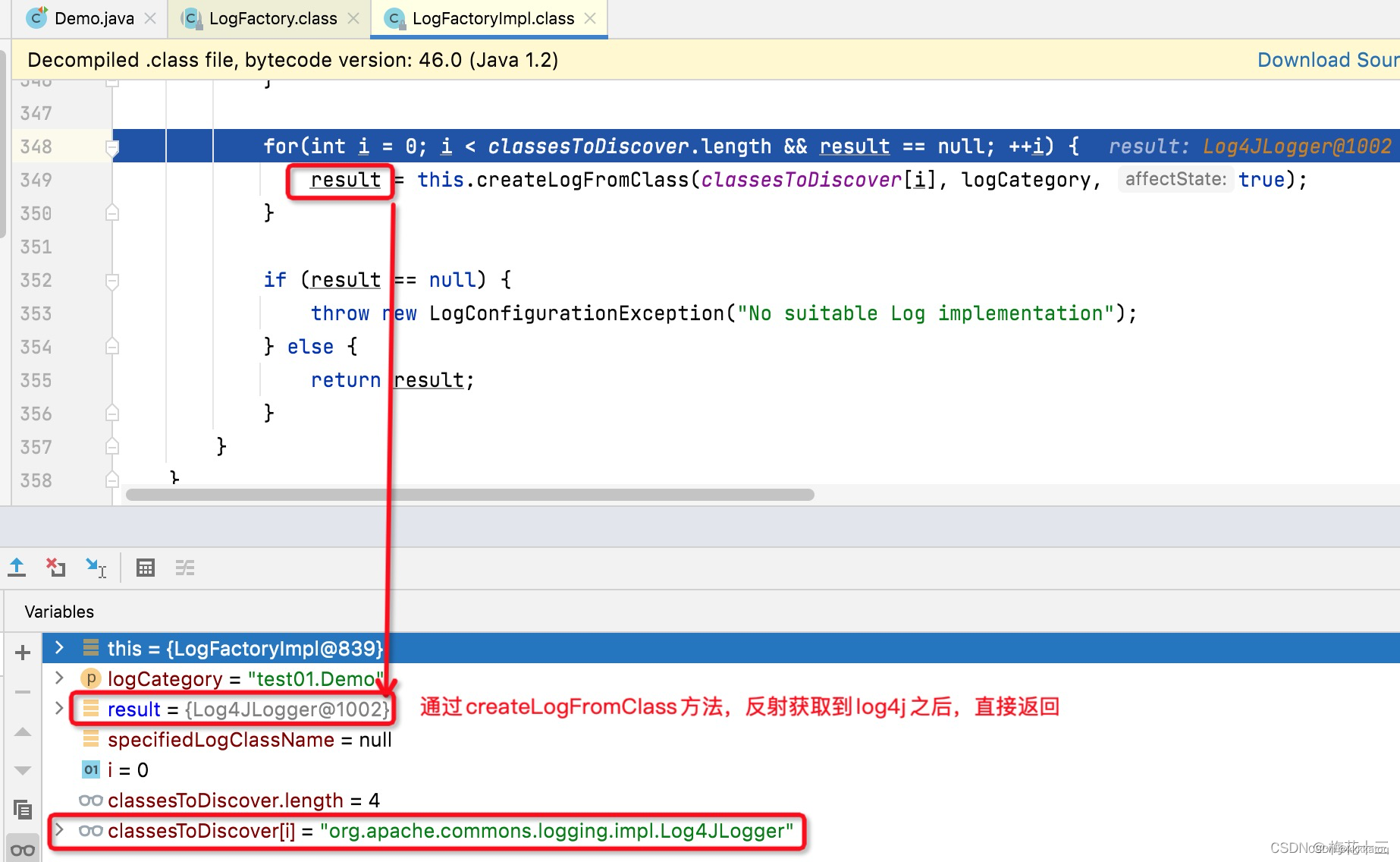
java日志框架总结(四 、JCL日志门面技术)
日志框架出现的历史顺序:Log4j → JUL → JCL → slf4j → logback → log4j2 一、背景 在前面博文中,我们分别讲述了常用的2个日志框架:JUL(Java Util Logging)、Log4J。那么如何选择使用哪一个呢? 根据项…...
mfc140.dll丢失的几种修复方式,有效的解决文件丢失问题
mfc140.dll是Microsoft Foundation Class (MFC)库中的一个非常重要的DLL文件。它承载了许多被执行程序使用的函数和资源。这个库主要被广泛应用于开发Windows操作系统上的应用程序。然而,有时候我们可能会遭遇到mfc140.dll缺失或损坏的情况,这会导致依赖…...
从一个小故事讲解观察者模式~
定义对象间的一种一对多的依赖关系,当一个对象的状态发生改变时,所有依赖于它的对象都得到通知并被自动更新。 什么是观察者模式? 观察者模式在我们的日常生活中极其常见。 先来看看观察者模式的定义: 观察者模式定义了对象之间…...
LeetCode、1137. 第 N 个泰波那契数【简单,动态规划】
文章目录 前言LeetCode、1137. 第 N 个泰波那契数【简单,动态规划】题目与分类思路一维动态规划 资料获取 前言 博主介绍:✌目前全网粉丝2W,csdn博客专家、Java领域优质创作者,博客之星、阿里云平台优质作者、专注于Java后端技术…...
Python爬虫urllib详解
前言 学习爬虫,最初的操作便是模拟浏览器向服务器发出请求,那么我们需要从哪个地方做起呢?请求需要我们自己来构造吗?需要关心请求这个数据结构的实现吗?需要了解 HTTP、TCP、IP 层的网络传输通信吗?需要知…...
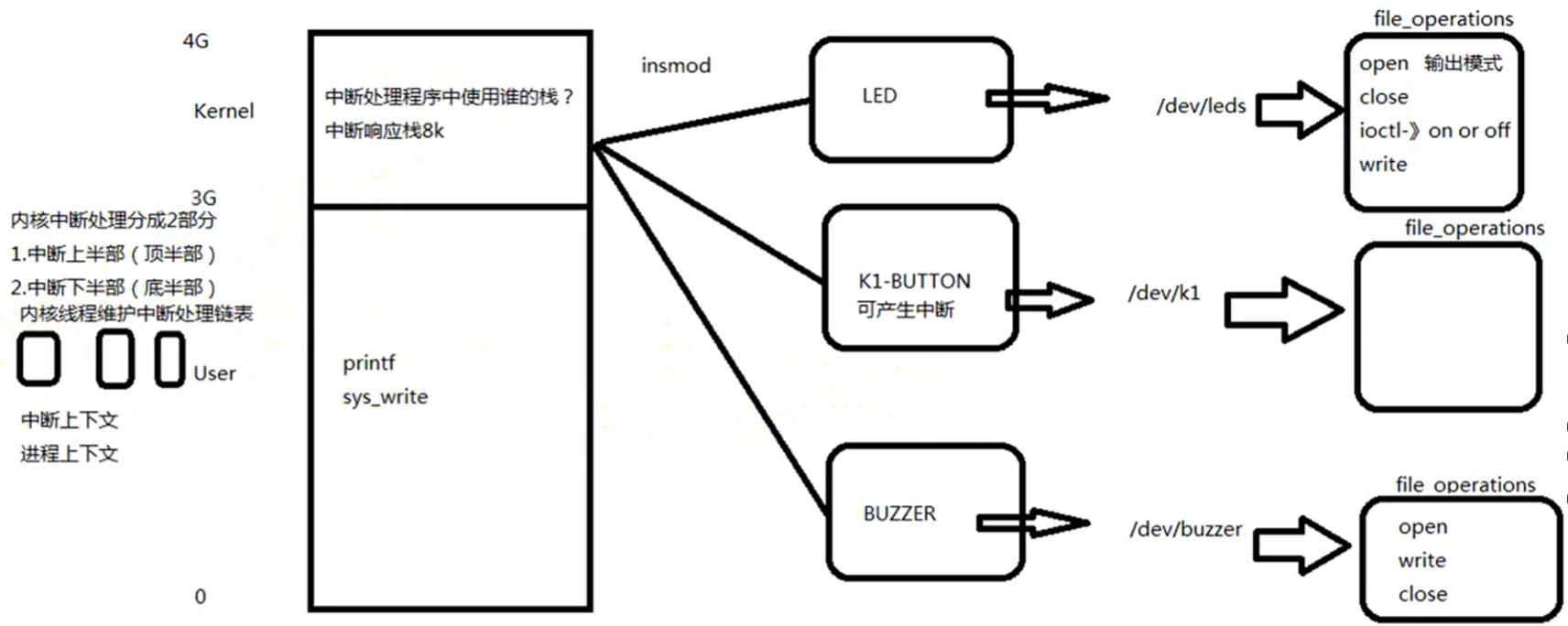
Linux嵌入式开发+驱动开发-中断
swi汇编指令可以产生软中断,以下是硬件中断的产生到执行完毕的全过程: 在自己设计的芯片“CPU响应中断”程序的第四个步骤可以转向“中断向量控制器”,中断向量控制器中存储中断元服务地址即处理中断处理程序的地址,而不用使用0X1…...

android tv开发-1,leanback
目录 1.leanback库的一些事 2.leanback在使用时遇到的一些麻烦 视频卡片 页面空白 关于左侧菜单的一些设置 数据加载异常与加载中的一些操作 如果页面无数据,如何显示错误的页面....
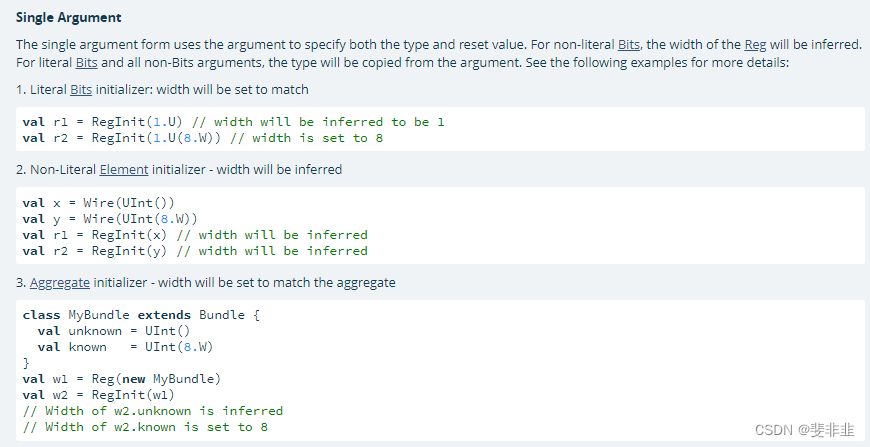
chisel RegInit/UInt/U
val reg RegInit(0.U(8.W)) //ok val reg RegInit(0.UInt(8.W)) //errU 使用在数字 . 后边50.U UInt 使用在IO(new Bundle val a Input(UInt(8.W)) 或者 def counter(max:UInt, a1:UInt) package emptyimport chisel3._ import chisel3.util._class MyCounter extends …...
)
华为OD机试真题-田忌赛马-2024年OD统一考试(C卷)
题目: 给定两个只包含数字的数组a,b,调整数组 a 里面数字的顺序,使得尽可能多的 a[i] >b[i]。数组 a和 b 中的数字各不相同。 输出所有可以达到最优结果的 a 数组的数量 输入描述: 输入的第一行是数组 a 中的数字,其中只包含数字,每两个数字之间相隔一个空格,a 数组…...

QMUI_Android:提升Android开发效率与质量的利器
QMUI_Android:提升Android开发效率与质量的利器 在Android应用开发过程中,开发者常常面临着重复编写基础组件和处理兼容性问题的挑战,这不仅耗费时间,也降低了开发效率。为了解决这一问题,Tencent推出了QMUI_Android框…...
如何部署Linux AMH服务器管理面板并结合内网穿透远程访问
文章目录 1. Linux 安装AMH 面板2. 本地访问AMH 面板3. Linux安装Cpolar4. 配置AMH面板公网地址5. 远程访问AMH面板6. 固定AMH面板公网地址 AMH 是一款基于 Linux 系统的服务器管理面板,它提供了一系列的功能,包括网站管理、FTP 管理、数据库管理、DNS 管…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...











