编译原理与技术(三)——语法分析(二)自顶向下-递归下降
一、语法分析的两种方法
自顶向下(Top-down):
针对输入串,从文法的开始符号出发,尝试根据产生式规则推导(derive)出该输入串。
从根部开始构造语法树。
自底向上(Bottom-up):
针对输入串,尝试根据产生式规则归约(reduce)到文法的开始符号。
从叶子开始构造语法树。
二、递归下降法

举个例子。

开始递归下降语法分析。




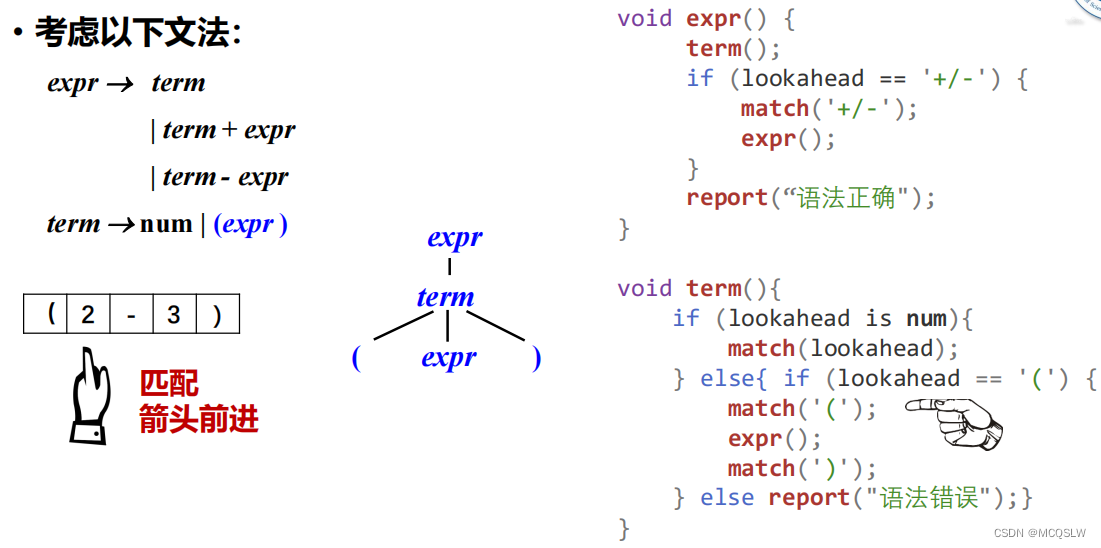

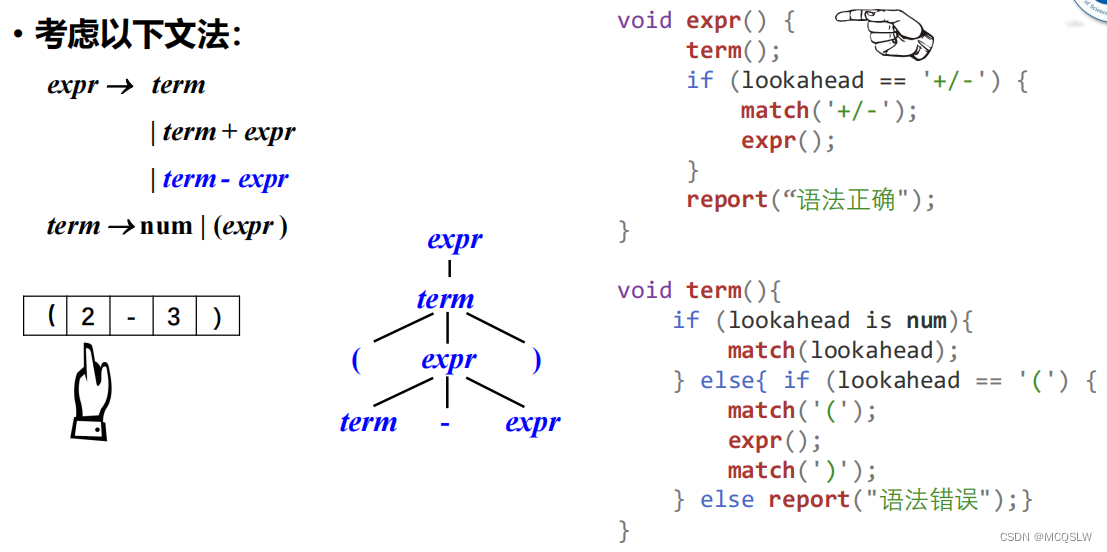
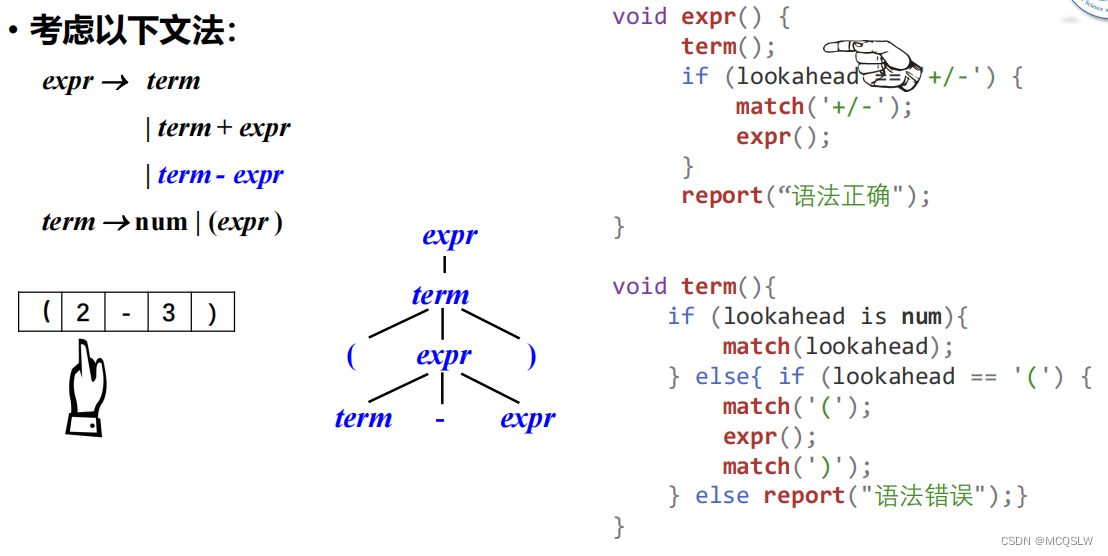

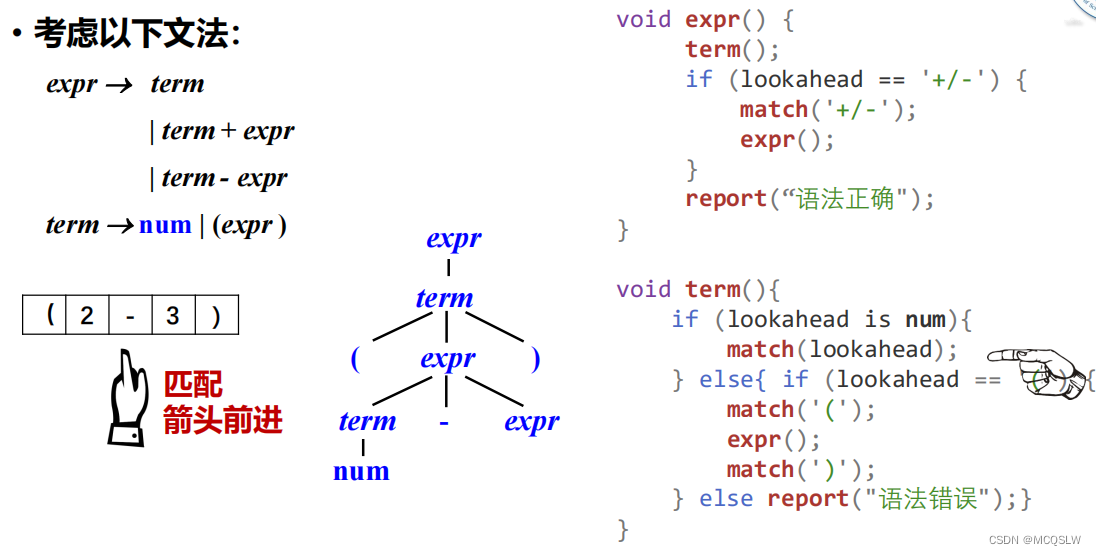
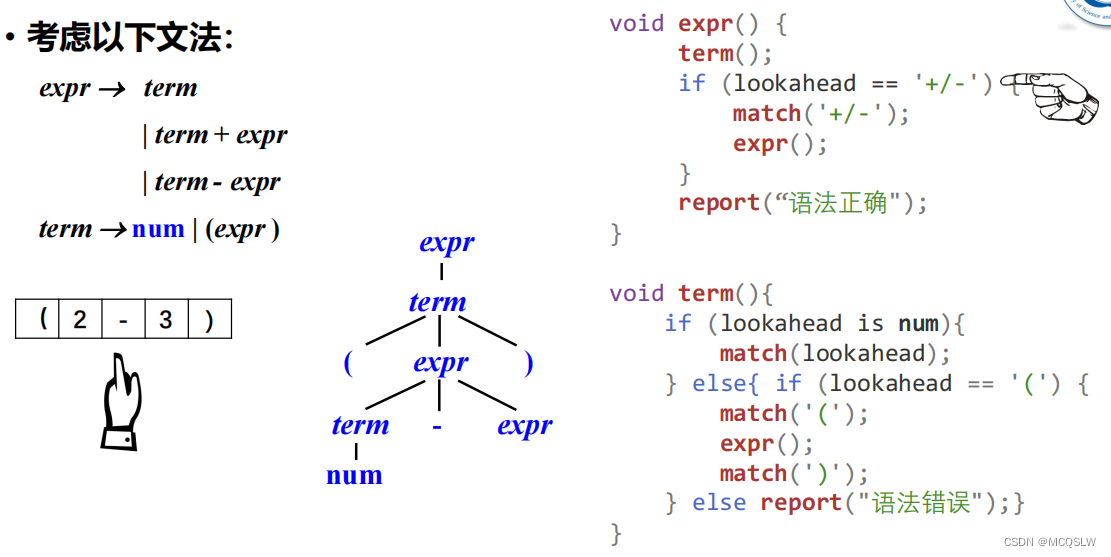

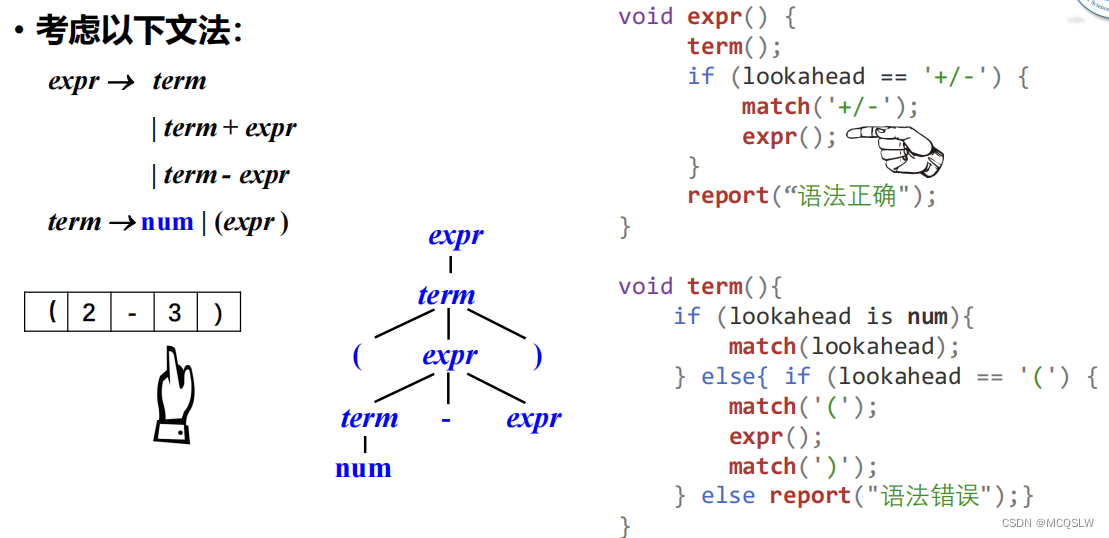
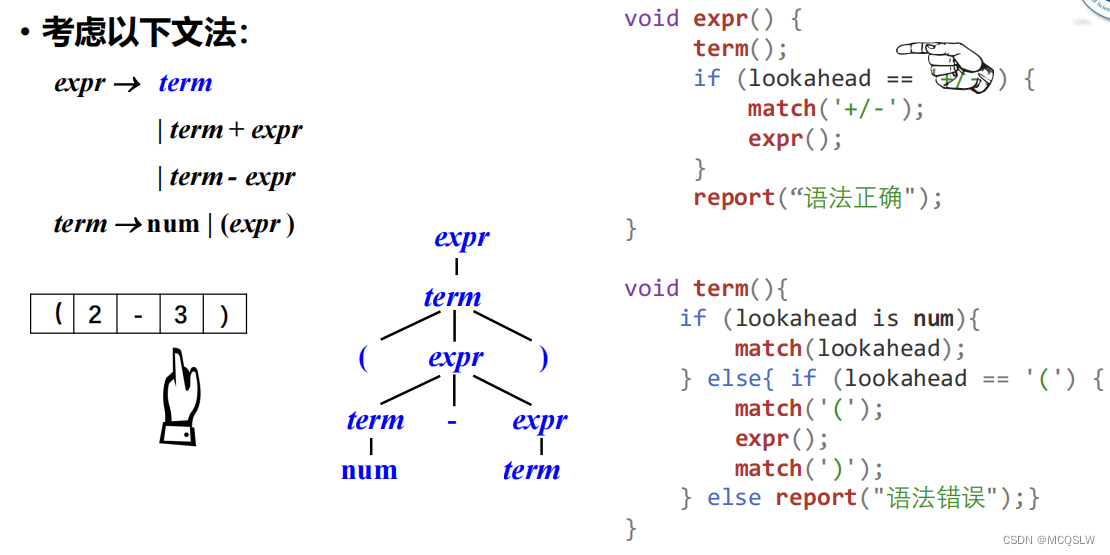

匹配到数字”3”后,程序从expr返回。


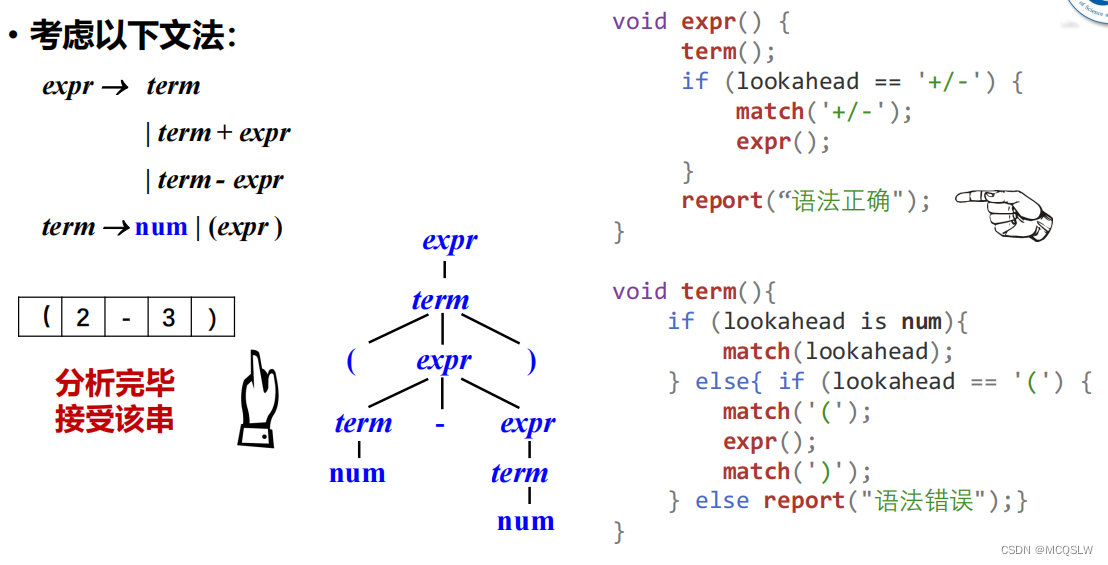
至此,递归下降分析结束。
三、递归下降法存在的问题及解决方法
(一)陷入无限左递归中
首先介绍什么是文法的递归。
若文法G存在推导:A ---> aAb,那么就称文法G是一个递归文法。
当文法G的唯一一个递归推导A ---> aAb中的a是空串时,就称文法G是一个左递归文法。同样可以定义右递归文法。
左递归又可分为直接左递归和间接左递归。



解决方法:消除直接左递归。

消除左递归的通用方法

上面的方法是消除直接左递归。
遇见了间接左递归时,要将文法先变换为直接左递归,再消除直接左递归。

(二)如何选择推导式
当遇见有左公因子的文法时。
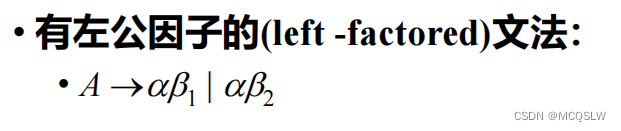
语法分析要选择一个进行推导,为了获取足够多的信息来做出正确的选择,我们尽可能延迟对该产生式的决策。而我们实现延迟决策的方法就是提取左公因子。

典型的例子是if-else语句的文法。

(三)复杂的回溯

参考资料:
[1]USTC 编译原理和技术 2023 (ustc-compiler-principles.github.io)
相关文章:

编译原理与技术(三)——语法分析(二)自顶向下-递归下降
一、语法分析的两种方法 自顶向下(Top-down): 针对输入串,从文法的开始符号出发,尝试根据产生式规则推导(derive)出该输入串。 从根部开始构造语法树。 自底向上(Bottom-up&#…...
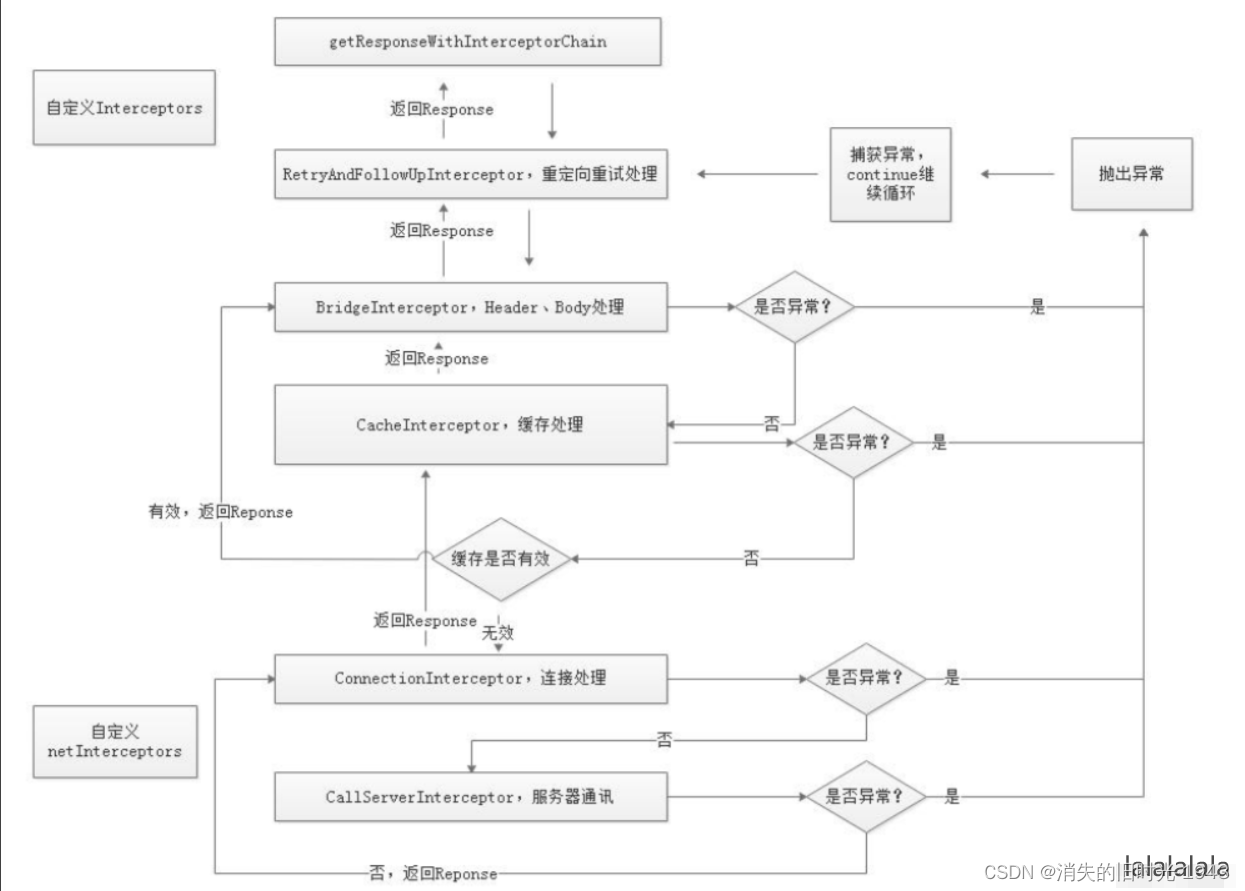
okhttp 的 拦截器
拦截器有很多作用,实现就是责任链模式,细节,等我有时间补上。 后面有时间更新一下。 OkHttp最核心的工作是在 getResponseWithInterceptorChain() 中进行,在进入这个方法分析之前,我们先来了 解什么是责任链模式&…...

Android:多线程下载网络图片
3.12 网络图片操作 1、通过URL请求获取网络图片 示例: 创建t_picture.xml,页面layout布局文件,一个Button按钮和一个ImageView容器显示图片。 <?xml version="1.0" encoding="utf-8"?><LinearLayout xmlns:android="http://schemas.a…...

跟着GPT学设计模式之原型模式
如果对象的创建成本比较大,而同一个类的不同对象之间差别不大(大部分字段都相同),在这种情况下,我们可以利用对已有对象(原型)进行复制(或者叫拷贝)的方式来创建新对象&a…...

博客|基于Springboot的个人博客系统设计与实现(源码+数据库+文档)
个人博客系统目录 目录 基于Springboot的个人博客系统设计与实现 一、前言 二、系统功能设计 三、系统实现 1、管理员功能实现 (1)用户管理 (2)文章分类管理 (3)公告信息管理 (4&#…...

【gcc】webrtc发送侧计算 丢包率
大神的分析 : 提到: 每当收到cc-feedback或者收到RR-report的时候就能统计出丢包率,在cc-controller中就会调用SendSideBandwidthEstimation::UpdatePacketsLost()去更新丢包率,同时进行码率预估 G:\CDN\rtcCli\m98\src\modules\congestion_controller\goog_cc\send_side_b…...

elementui上传文件不允许重名
需求: 用户可以多文件上传 ,在上传到服务器之前需要检查服务器中有无重名的文件,如果有会返回重名文件的名称数组,这些文件需要一个一个的向用户确认是否要覆盖重传。确认完毕后再上传到服务器。 检查文件重名: //上传…...

鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之Video媒体组件
鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之Video媒体组件 一、操作环境 操作系统: Windows 10 专业版、IDE:DevEco Studio 3.1、SDK:HarmonyOS 3.1 二、Video媒体组件 用于播放视频文件并控制其播放状态的组件。 子组件 无 接口…...
Linux操作系统运维-Docker的基础知识梳理总结
Linux操作系统运维-Docker的基础知识梳理总结 docker用来解决不同开发人员软件调试时环境不统一的问题,保证了程序调试时运行环境的一致性。docker的设计理念便是一处镜像,处处运行,即通过产生用户软件,运行环境及其运行配置的统一…...

PMP考试成绩如何查询?
PMP考试成绩已经陆续出来了,出成绩时间大概一周左右,没收到的别着急,先把如何查询成绩路径弄清楚。 【如何查询成绩】 1、输入网址(PMI官网,不知道网址的私戳),点击 Log In 如果忘记 PMI 的账…...

【Scala】 2. 函数
2. 函数 scala运算符、if … else …两部分和C语言类型,这里不再赘述,这里从for循环开始讲讲scala和c/c的不同之处。 2.1 for循环 scala中主要包含to和until两个关键字,下面分别看看两者的用法,看例子就行了。 (1) to的用法 …...
14.0 Zookeeper环球锁实现原理
全局锁是控制全局系统之间同步访问共享资源的一种方式。 下面介绍zookeeper如何实现全民锁,讲解他锁和共享锁两类全民锁。 排他锁 排他锁(Exclusive Locks),又被称为写锁或独占锁,如果事务T1对数据对象O1加上排他锁…...

课时16:本地变量_普通变量
2.2.2 普通变量 学习目标 这一节,我们从 基础知识、简单实践、小结 三个方面来学习。 基础知识 变量分类 所谓的本地变量就是:在当前系统的某个环境下才能生效的变量,作用范围小。本地变量按照变量值的生成方式包含两种:普通…...
阿里云服务器centos_7_9_x64位,3台,搭建k8s集群
目录 1.环境信息 2.搭建过程 2.1 安装Docker源 2.2 安装Docker 2.3 安装kubeadm,kubelet和kubectl 2.4 部署Kubernetes Master(node1) 2.5 安装Pod网络插件(CNI) 2.6 加入Kubernetes Node 2.7 测试kubernetes集群 3.部署 Dashboard…...

代码随想录第二十八天
第七章 回溯算法part04 ● 93.复原IP地址 ● 78.子集 ● 90.子集II 详细布置 93.复原IP地址 本期本来是很有难度的,不过 大家做完 分割回文串 之后,本题就容易很多了 题目链接/文章讲解:https://programmercarl.com/0093.%E5…...

【python】绘制爱心图案
以下是一个简单的Python代码示例,它使用turtle模块绘制一个代表爱和情人节的心形图案。 首先,请确保计算机上安装了Python和turtle模块。然后,将以下代码保存到一个.py文件中,运行它就可以看到爱心图案的绘制过程。 import turt…...
在 Elastic Agent 中为 Logstash 输出配置 SSL/TLS
要将数据从 Elastic Agent 安全地发送到 Logstash,你需要配置传输层安全性 (TLS)。 使用 TLS 可确保你的 Elastic Agent 将加密数据发送到受信任的 Logstash 服务器,并且你的 Logstash 服务器从受信任的 Elastic Agent 客户端接收数据。 先决条件 确保你…...

Vue中对虚拟DOM的理解
作为现代前端开发中的主流框架之一,Vue.js是一个非常流行的JavaScript框架,其核心概念之一就是虚拟DOM(Virtual DOM)。在本篇文章中,我们将深入探讨Vue中虚拟DOM的概念,并讨论为什么它在前端开发中如此重要…...

golang通用后台管理项目——Go+Vue通用后台管理项目实战
GoVue通用后台管理项目实战 1、掌握组件中业务逻辑抽离的方法 2、掌握jwt,日志,跨域,鉴权中间件的使用 3、掌握基于gorm的sql多表查询 4、掌握gin-swag的应用 5、掌握go语言开发前后端分离项目的能力 6、从0到1开发完整前后端分离项目的能力 技术栈: go后端 ging…...

推动海外云手机发展的几个因素
随着科技的不断发展,海外云手机作为一种新兴技术,在未来呈现出令人瞩目的发展趋势。本文将在用户需求、技术创新和全球市场前景等方面,探讨海外云手机在未来的发展。 1. 用户需求的引领: 随着人们对移动性和便捷性的需求不断增长&…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...
