【Algorithms 4】算法(第4版)学习笔记 05 - 2.2 归并排序
文章目录
- 前言
- 参考目录
- 学习笔记
- 1:归并排序的简单演示
- 1.1:基本思路
- 1.2:归并排序的 demo 演示
- 1.3:代码实现
- 2:自顶向下的归并排序
- 2.1:比较次数与访问次数的证明
- 2.2:代码优化
- 2.3:优化后代码实现
- 3:自底向上的归并排序
- 3.1:代码实现
- 4:排序算法的复杂度
- 5:稳定性
- 5.1:插入排序:稳定
- 5.2:选择排序:不稳定
- 5.3:希尔排序:不稳定
- 5.4:归并排序:稳定
前言
本章节主要内容是 归并排序,除此之外还有 排序算法的复杂度 以及 稳定性 的相关内容。
本章节中间有穿插说明 比较器(Compartor),不过本文暂且略过这一内容,感兴趣的朋友建议移步视频自行学习总结。
参考目录
- B站 普林斯顿大学《Algorithms》视频课
(请自行搜索。主要以该视频课顺序来进行笔记整理,课程讲述的教授本人是该书原版作者之一 Robert Sedgewick。) - 微信读书《算法(第4版)》
(本文主要内容来自《2.2 归并排序》) - 官方网站
(有书本配套的内容以及代码)
学习笔记
注1:下面引用内容如无注明出处,均是书中摘录。
注2:所有 demo 演示均为视频 PPT demo 截图。
1:归并排序的简单演示
1.1:基本思路
归并排序基本思路:
- 数组一分为二
- 每一半 递归 排序
- 合并两半
1.2:归并排序的 demo 演示
对于归并排序,Sedgewick 教授的视频进行了分步演示,下面截图进行简单说明。
排好序的两个子数组:
在原数组的基础上复制一个辅助数组:
需要三个下标来进行操作:
i、j分别是两个比较的子数组的下标,k是原数组的下标。
比较两个子数组的数据,将较小的值放回原数组:
如果两个值相同,则将左侧子数组的值放回原数组:
如果其中一个子数组已经没有元素,则另一个子数组的元素直接放回原数组:
1.3:代码实现
edu.princeton.cs.algs4.Merge#merge

edu.princeton.cs.algs4.Merge#sort

2:自顶向下的归并排序
上面分步实现的归并排序是属于自顶向下的归并排序。官网给出了归并的分步结果图:
(截图自官网)
2.1:比较次数与访问次数的证明
比较次数和访问次数是衡量一个算法优劣与否的重要参考标准,因此这里给出了相关的证明。
(截图自视频 PPT)
每次归并最多需要访问数组6N次:
- 2N次用来复制
- 2N次用来将排好序的元素移动回去
- 另外最多比较2N次
视频中,教授使用长度 N 为 2n 的数组来证明:
D ( N ) = 2 D ( N / 2 ) + N , N > 1 ,且 D ( 1 ) = 0 D(N) = 2D(N/2) + N,N>1,且 D(1) = 0 D(N)=2D(N/2)+N,N>1,且D(1)=0
一共有三种证明方式,但说实话我看了几遍还是没太懂怎么算的(哭),先把证明方式贴出来:
方式一:图形法证明
方式二:数学方式证明
方式三:数学归纳法证明
这里再贴一下书里面的相关证明帮助理解:
命题F。对于长度为N的任意数组,自顶向下的归并排序需要½NlgN至NlgN次比较。
书中关于命题 F 的证明,相对来说容易理解一些,可以自行参考学习。
2.2:代码优化
归并排序虽然速度比较快,但是也有一些缺点,因此也提出了一些优化方案:(这里列出对应的章节)
- 2.2.2.1 对小规模子数组使用插入排序
- 2.2.2.2 测试数组是否已经有序
- 2.2.2.3 不将元素复制到辅助数组
2.3:优化后代码实现
edu.princeton.cs.algs4.MergeX#sort

3:自底向上的归并排序
自顶向下的归并排序使用了递归的方式,为了减少递归的操作,又提出了自底向上的归并排序。
(截图自官网)
3.1:代码实现
edu.princeton.cs.algs4.MergeBU#sort

4:排序算法的复杂度
这里使用了决策树来进行说明,不过我觉得这一部分书本的说明不是很好,有些地方说得云里雾里的……
例如:
一眼看过去不知道是啥。然后看教授的PPT:
还有对于命题 I 的描述,每一个字我都认识,愣是读了好几遍才读通顺:
命题I。没有任何基于比较的算法能够保证使用少于lg(N!)~NlgN次比较将长度为N的数组排序。
再来看看视频里是怎么说的:
Any compare-based sorting algorithm must use at least lg(N!)~NlgN compares in the worst-case.
任何基于比较的排序算法,在最坏的情况下需要使用 lg(N!)~NlgN 次比较。
贴一下完整的 PPT 截图,一目了然:
证明:
- 假设数组由N个不同的值 a1 到 aN 组成。
- 最坏的情况由决策树的 高度 h 决定。
- 高度为 h 的二叉树最多有 2h 叶子节点。
- N! 不同的排序 => 至少 N! 叶子节点。
根据书里面的说明再完善一下:
从比较树观察得到的第一个重要结论是这棵树应该至少有 N! 个叶子结点,因为 N 个不同的主键会有 N! 种不同的排列。
二叉树的一个基本的组合学性质就是高度为 h 的树最多只可能有 2h 个叶子结点,拥有 2h 个结点的树是完美平衡的,或称为完全树。
5:稳定性
这一部分回顾了目前所讲到的四种算法:插入排序、选择排序、希尔排序以及归并排序。
Q:哪些算法是稳定的?
A:插入排序和归并排序。(选择排序和希尔排序不稳定。)
5.1:插入排序:稳定
插入排序中,相同的值不会越过彼此。
通常而言,看一个排序是否稳定,一般是看它是否有长距离的交换可能使得一条记录越过某一条相同值的记录。
5.2:选择排序:不稳定
5.3:希尔排序:不稳定
5.4:归并排序:稳定
只要归并操作是稳定的,那么归并排序算法就是稳定的;操作是否稳定,取决于代码怎么写。
(完)
相关文章:

【Algorithms 4】算法(第4版)学习笔记 05 - 2.2 归并排序
文章目录 前言参考目录学习笔记1:归并排序的简单演示1.1:基本思路1.2:归并排序的 demo 演示1.3:代码实现2:自顶向下的归并排序2.1:比较次数与访问次数的证明2.2:代码优化2.3:优化后代…...

mybatis mapper sql include用法实现sql块复用
一、总SQL <select id"getxxxMonitorData"resultType"com.xxx.module.system.dal.dataobject.xxx.xxxDO"><include refid"getxxxMonitorDataBaseSql"></include><include refid"whereContent"></include&…...
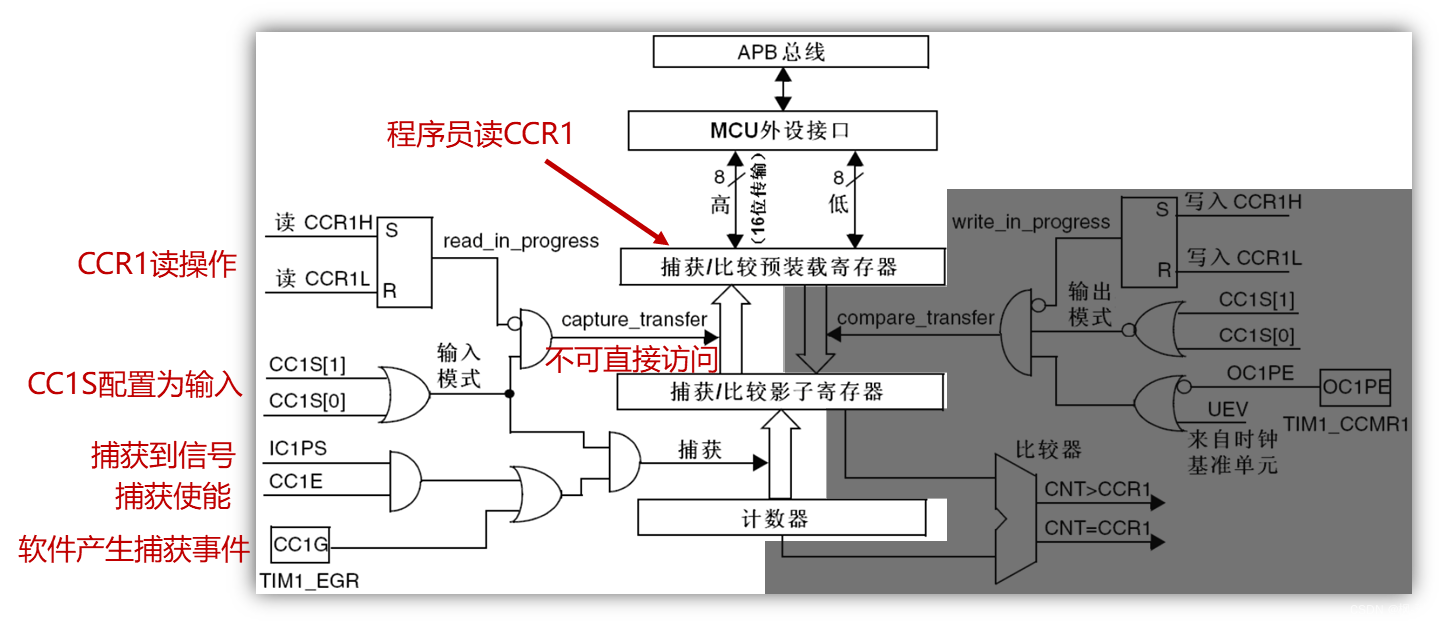
正点原子--STM32通用定时器学习笔记(2)
1. 通用定时器输入捕获部分框图介绍 捕获/比较通道的输入部分(通道1) 采样频率:控制寄存器 1(TIMx_CR1)的CKD[1:0] ⬇⬇⬇滤波方式选择: 捕获/ 比较模式寄存器 1(TIMx_CCMR1)的输入捕获部分⬇⬇…...

Flask实现异步调用sqlalchemy的模型类
事情是这样的,我这边需要在一次请求里面,搞一个异步不阻碍的任务,来执行耗时的操作。 一开始,我准备写的代码是这样的: from flask import Flask import time from concurrent.futures import ThreadPoolExecutorexec…...

Pocket2Mol + Generation of Atom Positions生成原子位置的方法有什么?联合概率是什么?
联合概率: 联合概率是统计学中的一个概念,用于描述两个或多个随机事件同时发生的概率。当我们谈论多个变量的联合概率时,我们是在探讨这些变量同时取特定值的概率。 让我们简化一下概念: 假设你有一个骰子(六面&…...

区分手机小程序以及电脑小程序;左滑、导航键返回拦截
1、区分电脑小程序和手机小程序 //区分电脑小程序、手机小程序(目标:手机小程序) // #ifdef MP-WEIXIN uni.getSystemInfo({success: (res) > {// windows | mac为pc端// android | ios为手机端// console.log(getSystemInfo,, res.plat…...

Web APIs 2 事件
Web APIs 2 事件 事件监听案例:广告关闭案例:随机问答 事件监听版本事件类型案例:轮播图完整焦点事件键盘事件输入事件案例:评论字数统计 事件对象获取事件对象事件对象常用属性案例:评论回车发布 环境对象this回调函数…...

网易腾讯面试题精选----90道设计模式面试题及答案
介绍 设计模式是软件开发的重要组成部分,为常见设计问题提供经过验证的解决方案。就设计模式面试候选人可以帮助衡量他们对软件架构的理解、解决问题的能力以及编写可维护和可扩展代码的能力。以下是一些常见的设计模式面试问题和答案,可帮助评估候选人在该领域的知识和专业知…...

程序员的数字化工作台:理解不关机背后的逻辑与需求
目录 程序员为什么不喜欢关电脑? 电脑对程序员的重要性: 工作流程与需求: 数据安全与备份: 即时性与响应: 个人习惯等方面: 程序员为什么不喜欢关电脑? 电脑对程序员的重要性:…...

Java Socket Server TCP服务端向指定客户端发送消息
实现思路 首先需要知道java里如何创建一个Socket服务器端。 //创建一个服务器端对象ServerSocket server new ServerSocket(); //绑定启动的ip和端口号server.bind(new InetSocketAddress("127.0.0.1",8082));//启动成功后,调用accept()方法阻塞…...
java日志框架总结(五、logback日志框架)
一、logback概述 Logback是由log4j创始人设计的又一个开源日志组件。 Logback当前分成三个模块: 1、logback-core, 2、logback- classic 3、logback-access。 1)logback-core是其它两个模块的基础模块。 2)logback-…...

android下library打包aar并上传到maven,嵌入版的app
android嵌入版 准备工作简化代码到三方app上传maven自动打包上面已经完成了library到三方app的流程 这几天在研究android下怎么把自己的项目当作一个library给到另一个app做嵌入使用,把这些记录下来,方便以后参考 准备工作 1.需要了解一些gradle 命令打…...

Xampp中Xdebug的安装使用
工欲善其事,必先利其器 XDebug简介 XDebug 是一个用于 PHP 的调试和性能分析工具。它提供了一系列功能,帮助开发者在开发和调试 PHP 应用程序时更加高效。 以下是 XDebug 的一些主要特性和功能: 调试功能: 断点调试:…...

金融行业的软件测试分析
随着金融行业的业务不断增加,金融交易模式的不断变化,金融机构对信息化的要求也越来越高,高质量的金融软件对于金融机构来说显得尤为重要。如何保证金融行业软件的质量,对金融行业软件的测试人员来说,也提出了更高的要…...
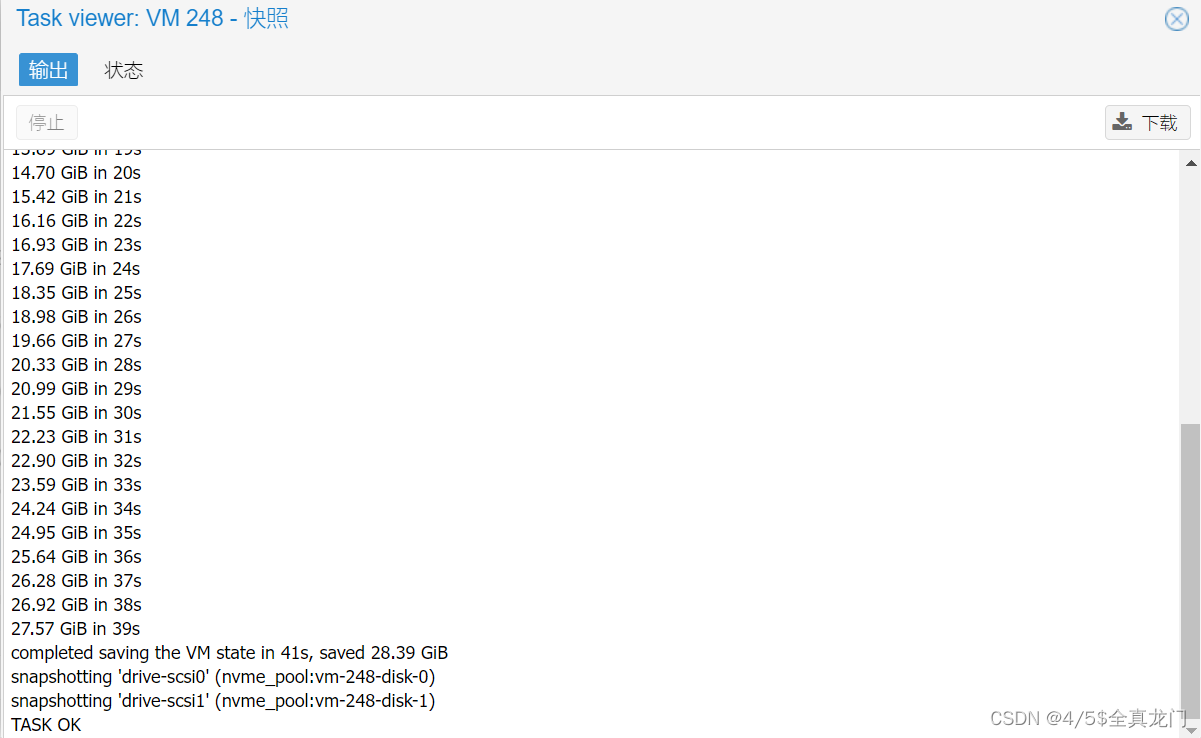
踩坑了,MySQL数据库生成大量奇怪的大文件
作者:田逸(formyz) 一大早就收到某个数据库服务器磁盘满的报警信息,其中数据盘使用率超过90%,如下图所示。 这是一台刚上线不久的MySQL从库服务器,数据盘的总容量是300G。先登录系统,查看主从同…...

ctfshow-web11~20-WP
web11 根据提示,查询对ctfshow域名进行dns查询,查看TXT记录 阿里云查询链接:阿里云网站运维检测平台 获取flag成功 web12 根据题目提示,我们访问robots.txt,获取到后台地址 然后我们访问一下后台...

2.5学习总结9
并查集 知识点 并查集是一种数据结构,用于处理一些不相交集合的合并及查询问题。它支持两种操作: Find(x):查找元素 x 所属的集合。Union(x, y):将元素 x 所属的集合和元素 y 所属的集合合并。 初始化:将每个元素单…...
删除.git的影响、git分支切换时注意事项
一、删除.git的影响 master分支文件 dev分支文件 删除.git后 文件为删除.git前分支的文件状态。 二、git分支切换时注意事项 情景:如果我在分支A,想要跳转到分支B。 git的规矩是,在那个分支上进行的提交,就算哪个分支上的工作…...

Linux系统调试课:硬件断点
沉淀、分享、成长,让自己和他人都能有所收获!😄 📢在linux内核编程中,经常会遇到由于内存被篡改,例如 buffer overflow,野指针,write after free等。查找分析此类问题非常的麻烦。 一、什么是硬件断点 硬件断点,是Linux内核中是一种被ptrace和内核内调试器使用调试…...
百卓Smart管理平台 uploadfile.php 文件上传漏洞复现(CVE-2024-0939)
0x01 产品简介 百卓Smart管理平台是北京百卓网络技术有限公司(以下简称百卓网络)的一款安全网关产品,是一家致力于构建下一代安全互联网的高科技企业。 0x02 漏洞概述 百卓Smart管理平台 uploadfile.php 接口存在任意文件上传漏洞。未经身份验证的攻击者可以利用此漏洞上传…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...

学习 Hooks【Plan - June - Week 2】
一、React API React 提供了丰富的核心 API,用于创建组件、管理状态、处理副作用、优化性能等。本文档总结 React 常用的 API 方法和组件。 1. React 核心 API React.createElement(type, props, …children) 用于创建 React 元素,JSX 会被编译成该函数…...

今日行情明日机会——20250609
上证指数放量上涨,接近3400点,个股涨多跌少。 深证放量上涨,但有个小上影线,相对上证走势更弱。 2025年6月9日涨停股主要行业方向分析(基于最新图片数据) 1. 医药(11家涨停) 代表标…...























