2.5学习总结9
并查集
知识点
并查集是一种数据结构,用于处理一些不相交集合的合并及查询问题。它支持两种操作:
- Find(x):查找元素 x 所属的集合。
- Union(x, y):将元素 x 所属的集合和元素 y 所属的集合合并。
初始化:将每个元素单独作为一个集合。
int father[10010];
void init(int n)
{for(int i=1;i<=n;i++)father[i]=i;
}查找:确定某个元素所属的集合。
int find(int i)
{if(i==father[i])return i;else father[i]=find(father[i]);return father[i];
}合并:将两个集合合并成一个集合。
void unionn(int i,int j)
{int x=find(i);int y=find(j);father[x]=y;
}并查集的时间复杂度为O(log*n),其中n是元素的个数。
P3367 【模板】并查集
题目描述
如题,现在有一个并查集,你需要完成合并和查询操作。
输入格式
第一行包含两个整数 N,M ,表示共有 N 个元素和 M 个操作。
接下来 M 行,每行包含三个整数 Zi,Xi,Yi 。
当 Zi=1 时,将 Xi 与 Yi 所在的集合合并。
当 Zi=2 时,输出 Xi 与 Yi 是否在同一集合内,是的输出 Y ;否则输出 N 。
输出格式
对于每一个 Zi=2 的操作,都有一行输出,每行包含一个大写字母,为 Y 或者 N 。
输入输出样例
输入 #1复制
4 7
2 1 2
1 1 2
2 1 2
1 3 4
2 1 4
1 2 3
2 1 4
输出 #1复制
N
Y
N
Y
说明/提示
对于 30%30% 的数据,N≤10,M≤20。
对于 70%70% 的数据,N≤100,M≤10^3。
对于 100%100% 的数据,1≤N≤10^4,1≤M≤2×10^5,1≤Xi,Yi≤N,Zi∈{1,2}。
#include<stdio.h>
int father[10010];
void init(int n)
{for(int i=1;i<=n;i++)father[i]=i;
}//初始化
int find(int i)
{if(i==father[i])return i;else father[i]=find(father[i]);return father[i];
}//查找
void unionn(int i,int j)
{int x=find(i);int y=find(j);father[x]=y;
}//合并
int main()
{int i,n,m,z,x,y;scanf("%d %d",&n,&m);init(n);for(i=1;i<=m;i++){scanf("%d %d %d",&z,&x,&y);if(z==1) unionn(x,y);else {if(find(x)==find(y))printf("Y\n");//祖先相同,位于同一集合else printf("N\n");}}
}P1111 修复公路
题目背景
A 地区在地震过后,连接所有村庄的公路都造成了损坏而无法通车。政府派人修复这些公路。
题目描述
给出 A 地区的村庄数 N,和公路数 M,公路是双向的。并告诉你每条公路的连着哪两个村庄,并告诉你什么时候能修完这条公路。问最早什么时候任意两个村庄能够通车,即最早什么时候任意两条村庄都存在至少一条修复完成的道路(可以由多条公路连成一条道路)。
输入格式
第 1 行两个正整数 N,M。
下面 M 行,每行 3 个正整数 x,y,t,告诉你这条公路连着 x,y 两个村庄,在时间t时能修复完成这条公路。
输出格式
如果全部公路修复完毕仍然存在两个村庄无法通车,则输出 −1,否则输出最早什么时候任意两个村庄能够通车。
输入输出样例
输入 #1复制
4 4
1 2 6
1 3 4
1 4 5
4 2 3
输出 #1复制
5
说明/提示
1≤x,y≤N≤10^3,1≤M,t≤10^5。
#include<bits/stdc++.h>
using namespace std;
struct road
{int x,y,t;
}a[100010],b;
bool operator < (road a,road b){return a.t<b.t;}
int father[1010];
void init(int n)
{for(int i=1;i<=n;i++)father[i]=i;
}//初始化
int find(int i)
{if(i==father[i])return i;return father[i]=find(father[i]);
}//查找
int main()
{int i,j,n,m,x,y,cnt=0,max=0;scanf("%d %d",&n,&m);init(n);for(i=1;i<=m;i++)scanf("%d %d %d",&a[i].x,&a[i].y,&a[i].t);sort(a+1,a+1+m);//对a[i].t排序for(i=1;i<=m;i++) {int x=find(a[i].x);int y=find(a[i].y);if(x==y)continue;father[x]=y;//合并cnt++;max=a[i].t<max?max:a[i].t;}if(cnt!=n-1)printf("-1");else printf("%d",max);
}P1455 搭配购买
题目描述
明天就是母亲节了,电脑组的小朋友们在忙碌的课业之余挖空心思想着该送什么礼物来表达自己的心意呢?听说在某个网站上有卖云朵的,小朋友们决定一同前往去看看这种神奇的商品,这个店里有 n 朵云,云朵已经被老板编号为 1,2,3,...,n,并且每朵云都有一个价值,但是商店的老板是个很奇怪的人,他会告诉你一些云朵要搭配起来买才卖,也就是说买一朵云则与这朵云有搭配的云都要买,电脑组的你觉得这礼物实在是太新奇了,但是你的钱是有限的,所以你肯定是想用现有的钱买到尽量多价值的云。
输入格式
第一行输入三个整数,n,m,w,表示有 n 朵云,m 个搭配和你现有的钱的数目。
第二行至 n+1 行,每行有两个整数,ci,di,表示第 i 朵云的价钱和价值。
第 n+2 至 n+1+m 行 ,每行有两个整数 ui,vi。表示买第 ui 朵云就必须买第 vi 朵云,同理,如果买第 vi 朵就必须买第 ui 朵。
输出格式
一行,表示可以获得的最大价值。
输入输出样例
输入 #1复制
5 3 10
3 10
3 10
3 10
5 100
10 1
1 3
3 2
4 2
输出 #1复制
1
说明/提示
-
对于 30%30% 的数据,满足 1≤n≤100;
-
对于 50%50% 的数据,满足 1≤n,w≤10^3,1≤m≤100;
-
对于 100%100% 的数据,满足 1≤n,w≤10^4,0≤m≤5×10^3。
一道并查集+01背包题,01背包的限制条件为买A必须买B,故可以用并查集将几个物品合成一个大物品,然后再用01背包问题做即可。
#include<bits/stdc++.h>
using namespace std;
int father[10010],c[10010],d[10010],dp[10010];
int find(int i)
{if(i==father[i])return i;return father[i]=find(father[i]);
}//查找
void unionn(int i,int j)
{int x=find(i);int y=find(j);if(x!=y){father[x]=y;c[y]=c[y]+c[x];d[y]=d[y]+d[x];}
}//合并物品,将价值,价钱分别相加
int main()
{int n,m,w,i,j;cin>>n>>m>>w;for(i=1;i<=n;i++){cin>>c[i]>>d[i];father[i]=i;}for(i=1;i<=m;i++){int x,y;cin>>x>>y;unionn(x,y);}for(i=1;i<=n;i++){if(father[i]==i){for(j=w;j>=c[i];j--)dp[j]=max(dp[j],dp[j-c[i]]+d[i]);}}//0-1背包问题解法printf("%d",dp[w]);
}
二分查找
知识点
二分查找是一种在有序数组中查找某一元素的算法。它的基本思想是将数组分为两部分,然后判断目标元素在左边还是右边,再在相应的部分中进行查找,重复这个过程,直到找到目标元素或者确定目标元素不存在。
具体步骤如下:
1. 声明两个指针,一个指向数组的开头,一个指向数组的末尾。
2. 计算数组中间元素的下标,可以使用 mid = ( low+high ) / 2。
3. 比较中间元素与目标元素的大小:
- 如果中间元素等于目标元素,说明找到了目标元素,返回其下标。
- 如果中间元素大于目标元素,说明目标元素在数组的左边,移动右指针到中间元素的前一个位置。
- 如果中间元素小于目标元素,说明目标元素在数组的右边,移动左指针到中间元素的后一个位置。
4. 重复步骤2和步骤3,直到找到目标元素或者确定目标元素不存在。
二分查找的时间复杂度是 O(log n),其中 n 是数组的长度。这是由于每次查找都将查找范围缩小一半。
int binarySearch(int arr[],int low,int high,int target)
{while(low<=high) {int mid=(low+high)/2;// 如果目标值等于中间值,则返回中间索引if (arr[mid]==target) return mid;// 如果目标值小于中间值,则在左半部分查找if (arr[mid]>target) high=mid-1;// 如果目标值大于中间值,则在右半部分查找if (arr[mid]<target) low=mid+1;}// 如果没有找到目标值,则返回-1return -1;
}P2759 奇怪的函数
题目描述
使得 x^x 达到或超过 n 位数字的最小正整数 x 是多少?
输入格式
一个正整数 n。
输出格式
使得 x^x 达到 n 位数字的最小正整数 x。
输入输出样例
输入 #1复制
11
输出 #1复制
10
说明/提示
对于全部数据,1≤n≤2×10^9。
#include<stdio.h>
#include<math.h>
int main()
{long long n,num,mid,low=1,high=2000000000;scanf("%lld",&n);while(low<high){mid=(low+high)/2;num=mid*log10(mid)+1;if(num<n) low=mid+1;else high=mid;}printf("%lld",low);
}P8800 [蓝桥杯 2022 国 B] 卡牌
题目描述
这天,小明在整理他的卡牌。
他一共有 n 种卡牌,第 i 种卡牌上印有正整数数 i(i∈[1,n]), 且第 i 种卡牌现有 ai 张。
而如果有 n 张卡牌,其中每种卡牌各一张,那么这 n 张卡牌可以被称为一套牌。小明为了凑出尽可能多套牌,拿出了 m 张空白牌, 他可以在上面写上数 i,将其当做第 i 种牌来凑出套牌。然而小明觉得手写的牌不太美观,决定第 i 种牌最多手写 bi 张。
请问小明最多能凑出多少套牌?
输入格式
输入共 3 行,第一行为两个正整数 n,m 。
第二行为 n 个正整数 a1,a2,…,an 。
第三行为 n 个正整数 b1,b2,…,bn 。
输出格式
一行,一个整数表示答案。
输入输出样例
输入 #1复制
4 5
1 2 3 4
5 5 5 5
输出 #1复制
3
说明/提示
【样例说明】
这 5 张空白牌中,拿 2 张写 1,拿 1 张写 2,这样每种牌的牌数就变为了 3,3,3,4,可以凑出 3 套牌,剩下 2 张空白牌不能再帮助小明凑出一套。
【评测用例规模与约定】
对于 30%30% 的数据,保证 n≤2000;
对于 100%100% 的数据,保证 n≤2×10^5;n≤2×105;ai,bi≤n;m≤n2 。
#include<bits/stdc++.h>
using namespace std;
long long a[200010],b[200010];
long long n,m;
long long low=0,high=1e7;
int check(int num)
{long long sum=0;for(int i=1;i<=n;i++){if(num-a[i]>b[i])return 0;sum=sum+max(num-a[i],(long long)0);}if(sum<=m) return 1;else return 0;
}
int cut()
{while(low+1<high){int mid=(low+high)/2;if(check(mid)==1)low=mid;else high=mid;}if(check(high)==1) return high;return low;
}
int main()
{cin>>n>>m;for(int i=1;i<=n;i++)scanf("%lld",&a[i]);for(int i=1;i<=n;i++)scanf("%lld",&b[i]);cout<<cut();
}相关文章:

2.5学习总结9
并查集 知识点 并查集是一种数据结构,用于处理一些不相交集合的合并及查询问题。它支持两种操作: Find(x):查找元素 x 所属的集合。Union(x, y):将元素 x 所属的集合和元素 y 所属的集合合并。 初始化:将每个元素单…...
删除.git的影响、git分支切换时注意事项
一、删除.git的影响 master分支文件 dev分支文件 删除.git后 文件为删除.git前分支的文件状态。 二、git分支切换时注意事项 情景:如果我在分支A,想要跳转到分支B。 git的规矩是,在那个分支上进行的提交,就算哪个分支上的工作…...

Linux系统调试课:硬件断点
沉淀、分享、成长,让自己和他人都能有所收获!😄 📢在linux内核编程中,经常会遇到由于内存被篡改,例如 buffer overflow,野指针,write after free等。查找分析此类问题非常的麻烦。 一、什么是硬件断点 硬件断点,是Linux内核中是一种被ptrace和内核内调试器使用调试…...
百卓Smart管理平台 uploadfile.php 文件上传漏洞复现(CVE-2024-0939)
0x01 产品简介 百卓Smart管理平台是北京百卓网络技术有限公司(以下简称百卓网络)的一款安全网关产品,是一家致力于构建下一代安全互联网的高科技企业。 0x02 漏洞概述 百卓Smart管理平台 uploadfile.php 接口存在任意文件上传漏洞。未经身份验证的攻击者可以利用此漏洞上传…...

关于RabbitMQ常见的十道面试题
RabbitMQ是如何组成的?它有哪些重要的组件? RabbitMQ主要由以下几个重要组件组成: Broker:这是消息代理,主要负责接收、存储和转发消息Exchanges:交换器,它的主要作用是根据一定的规则匹配消息…...

spring cloud stream
背景 主要解决不同消息中间件切换问题。实现不同中间件的代码解耦。 链接: 支持的中间件 后文使用kafka测试。 引入依赖 <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-stream</artifactId></depende…...
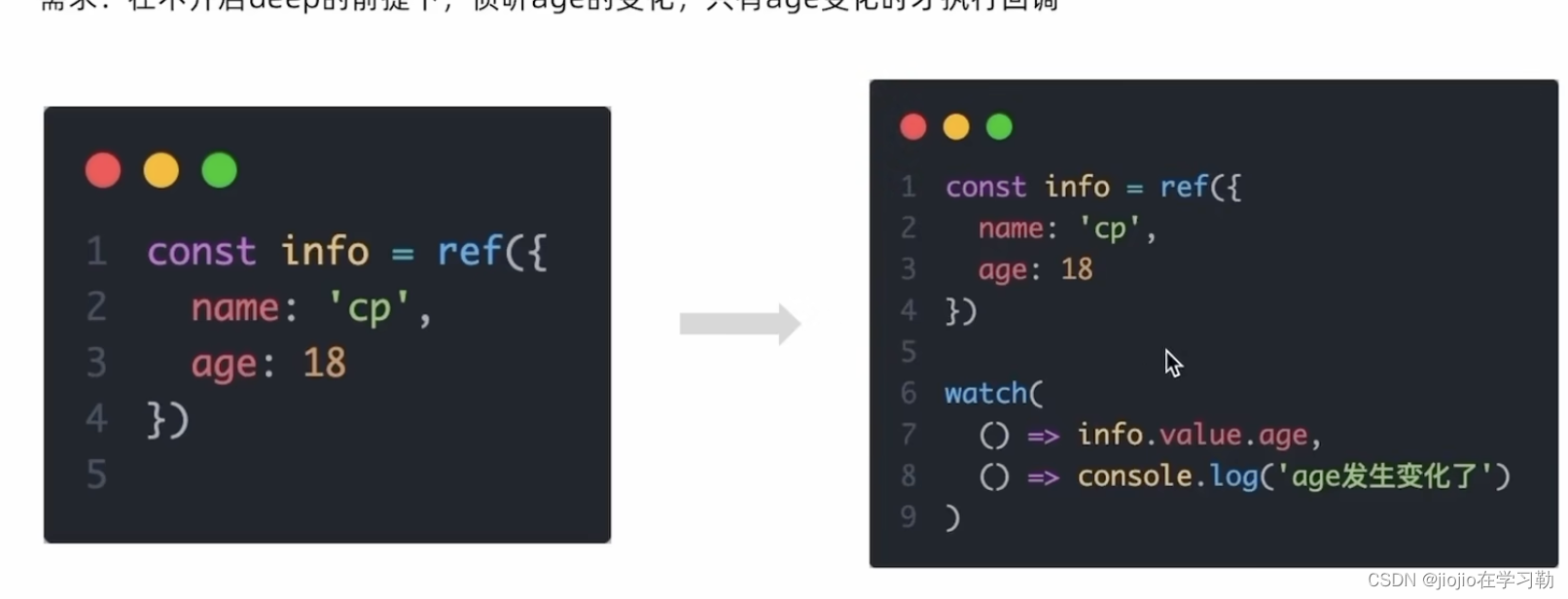
vue3 之 组合式API—watch函数
watch函数 作用:侦听一个或者多个数据的变化,数据变化时执行回调函数 两个额外参数: 1.immediate(立即执行)2.deep(深度侦听) 场景:比如选择不同的内容请求后端不同数据时 如下图 …...

并发容器【ConcurentHashMap、CopyOnWriteArrayList、阻塞队列、ArrayBlockingQueue】
并发容器 什么是并发容器?同步容器:并发容器: ConcurrentHashMap结构图JDK1.7结构图JDK1.8结构图 CopyOnWriteArrayList实现原理 并发队列阻塞队列ArrayBlockingQueue 转自极客时间 什么是并发容器? 在JUC包中,有一大部分是关于并发容器的,如Concurr…...

EmoLLM-心理健康大模型
宣传一下自己最近参与的开源 https://github.com/aJupyter/EmoLLM EmoLLM-心理健康大模型 EmoLLM 探索本项目的文档 查看Demo 报告Bug 提出新特性 EmoLLM 是一个能够支持 理解用户-支持用户-帮助用户 心理健康辅导链路的心理健康大模型,由 InternLM2 指令微…...

学成在线:采用XXL-JOB任务调度方案使用FFmpeg处理视频转码业务
分片技术方案 概述 XXL-JOB并不直接提供数据处理的功能,它只会给所有注册的执行器分配好分片序号,在向执行器下发任务调度的同时携带分片总数和当前分片序号等参数 设计作业分片方案保证多个执行器之间不会查询到重复的任务,保证任务不会重复执行 任…...
计算机毕业设计 | SpringBoot大型旅游网站 旅行后台管理系统(附源码)
1, 概述 1.1 项目背景 随着互联网技术的快速发展和普及,旅游行业逐渐转向线上,越来越多的游客选择在线预订旅游产品。传统的线下旅行社模式已不能满足市场需求,因此,开发一个高效、便捷的旅游网站成为行业的迫切需求…...

蓝桥杯----凑算式
这个算式中A~I代表1~9的数字,不同的字母代表不同的数字。 比如: 68/3952/714 就是一种解法, 53/1972/486 是另一种解法. 这个算式一共有多少种解法? 注意:你提交应该是个整数,不要填写任何多余的内容或说明性文字。 代码 public class _03凑算式 {static int a[] {1,2,3…...
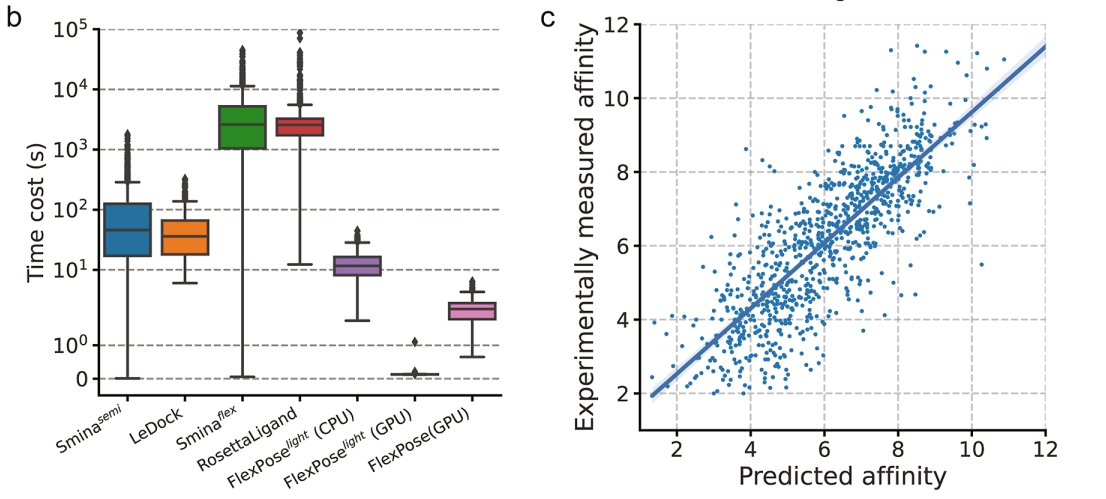
JCTC | 利用几何深度学习对蛋白质-配体结合pose进行等变灵活建模
Overview 该论文解决了药物开发中蛋白质-配体复合结构灵活建模的挑战。作者提出了一种名为FlexPose的新型深度学习框架,它可以直接对复杂结构进行建模,而不需要传统的采样和评分策略。 该模型结合了标量-向量双特征表示和 SE(3)等变网络设计来处理动态结…...

执行 terraform init 命令时 timeout 的解决方法
terrafrom 是一款常用来实现 IaC(基础设施即代码)的工具。通常的第一个命令往往是 terrafrom init。在执行此命令时,terrafrom 会根据已经配置好的 provdier 信息去下载安装对应云厂商的 provider。比如下面是一个腾讯云的 providerÿ…...

Docker Arthas 实战指南
Arthas 是一款强大的 Java 诊断和调试工具,它能够在生产环境中实时诊断 Java 应用,提供强大的调试功能,帮助开发者和运维人员解决各种 Java 应用的性能问题和调试挑战。本指南将介绍如何在 Docker 环境中使用 Arthas 进行实战。 官方文档 GitHub地址 …...

freertos 源码分析四 任务创建的简单分析
任务创建xTaskCreate 为TCB和TCB栈分配空间, 初始化,加入就绪任务链表 #if ( configSUPPORT_DYNAMIC_ALLOCATION 1 )BaseType_t xTaskCreate( TaskFunction_t pxTaskCode,const char * const pcName,const configSTACK_DEPTH_TYPE usStackDepth,void *…...

二叉树的锯齿形遍历,力扣
目录 题目: 我们直接看题解吧: 快速理解解题思路小建议: 解题方法: 相似题目对比分析: 解题分析: 解题思路: 补充说明: 思路优化: 代码实现(层序遍历倒序): 题…...

避免Arrays.asList陷阱:优雅处理结构性修改的方法
临近年终,项目交付排期比较紧张,导致很多时候,Code Review 往往是走马观花,没有严格执行。最近,一个实习生就产生了一个十分低级的代码BUG。笔者感觉这个问题,对于实习生,尤其是刚入职的 应届 J…...

微信小程序(三十六)事件传参
注释很详细,直接上代码 上一篇 新增内容: 1.传参步骤 2.传参接收解构步骤 源码: index.wxml <button type"primary" bind:tap"onclick" mark:index"{{0}}" mark:remb"{{1}}" class"But&quo…...

编译原理与技术(三)——语法分析(二)自顶向下-递归下降
一、语法分析的两种方法 自顶向下(Top-down): 针对输入串,从文法的开始符号出发,尝试根据产生式规则推导(derive)出该输入串。 从根部开始构造语法树。 自底向上(Bottom-up&#…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...

关于疲劳分析的各种方法
疲劳寿命预测方法很多。按疲劳裂纹形成寿命预测的基本假定和控制参数,可分为名义应力法、局部应力一应变法、能量法、场强法等。 1名义应力法 名义应力法是以结构的名义应力为试验和寿命估算的基础,采用雨流法取出一个个相互独立、互不相关的应力循环&…...

c++算法学习3——深度优先搜索
一、深度优先搜索的核心概念 DFS算法是一种通过递归或栈实现的"一条路走到底"的搜索策略,其核心思想是: 深度优先:从起点出发,选择一个方向探索到底,直到无路可走 回溯机制:遇到死路时返回最近…...

AGV|无人叉车工业语音播报器|预警提示器LBE-LEX系列性能与接线说明
LBE-LEX系列AGV|无人叉车工业语音播报器|预警提示器,涵盖LBE-LEI-M-00、LBE-LESM-00、LBE-LES-M-01、LBE-LEC-M-00、LBE-KEI-M-00、LBE-KES-M-00、LBE-KES-M-01、LBE-KEC-M-00等型号,适用于各种需要语音提示的场景,主要有AGV、AMR机器人、无人…...

基于 Transformer robert的情感分类任务实践总结之二——R-Drop
基于 Transformer robert的情感分类任务实践总结之一 核心改进点 1. R-Drop正则化 原理:通过在同一个输入上两次前向传播(利用Dropout的随机性),强制模型对相同输入生成相似的输出分布,避免过拟合。实现:…...
