【高质量精品】2024美赛B题22页word版高质量半成品论文+多版保奖思路+数据+前四问思路代码等(后续会更新)
一定要点击文末的卡片,进入后,获取完整论文!!

B 题整体模型构建
1. 潜水器动力系统失效:模型需要考虑潜水器在无推进力情况下的行为。
2. 失去与主船通信:考虑无法从主船接收指令或发送位置信息的情况。
3. 中性浮力和海底定位:潜水器可能位于海底或达到水下某个中性浮力点。 4. 水流和海水密度变化:影响潜水器位置的环境因素。
5. 海底地理:海底的地形可能会影响潜水器的最终位置或移动路径。
数学模型和公式
为预测潜水器的位置,我们可以建立基于物理学原理的动态模型,考虑力学和流体动力 学的因素。以下是潜水器运动的基本方程:
动力学方程
设潜水器的质量为 mm ,受到的浮力为 FbF_b ,重力为 FgF_g ,水流对潜水器施加 的力为 FcF_c ,潜水器在水中的阻力为 F_d ,则潜水器的运动方程可表示为:
md2r→dt2=Fb→+Fg→+Fc→− Fd→ m\frac{d^2\vec{r}}{dt^2} = \vec{F_b} + \vec{F_g} + \vec{F_c} - \vec{F_d}
其中, r →\vec{r} 是潜水器的位置向量, tt 是时间。
mm :潜水器的质量
Fb→\vec{F_b} :浮力,方向向上
Fg→=m ⋅ g\vec{F_g} = m \cdot g :重力,方向向下, gg 是重力加速度
Fc→\vec{F_c} :水流对潜水器的作用力,方向依赖于水流方向
Fd→\vec{F_d} :阻力,方向与潜水器运动方向相反,大小可以用 Fd=12ρv2CdAF_d =
\frac{1}{2} \rho v^2 C_d A 来估计,其中 ρ\rho 是水的密度, vv 是潜水器相对于水的速 度, CdC_d 是阻力系数,$A$ 是潜水器迎水面积
潜水器浮力和阻力的计算
浮力 FbF_b 可以通过潜水器排水量和水的密度来计算,阻力 FdF_d 可以根据潜水器的 形状、表面粗糙度和运动速度来估算。
数值解法
潜水器的运动方程是一个二阶微分方程,我们可以采 用数值方法(如欧拉方法或龙格-库塔方法)对其进行求解,得到潜水器随时间变化的 位置和速度。
模型假设
. 潜水器被视为质点,忽略其尺寸和形状的影响。
. 假设水流速度和方向是已知的,可以从海洋流动模型获得。
. 海底地形对潜水器运动的影响通过调整浮力和阻力参数来模拟。
通过上述模型和方法,我们可以预测在不同情况下潜水器的位置,为 MCMS 制定安全程 序提供科学依据。
为了解决上述复杂的数学建模问题,我们将问题分解为四个主要部分:定位、准备、搜 索和外推。下面是针对每个部分的详细分析和数学模型。
定位
模型构建
. 基于多传感器融合的动态预测模型:利用卡尔曼滤波(Kalman Filter)或扩展卡尔曼滤波 (Extended Kalman Filter, EKF)来整合来自潜水器内部(如 IMU 传感器)和外部(如声纳、 GPS 浮标)的多源信息,预测潜水器随时间变化的位置。
数学公式
假设潜水器的状态为 x →t= [xt,yt,zt,x˙t,y˙t,z˙t]T\vec{x}_t = [x_t, y_t, z_t, \dot{x}_t, \dot{y}_t, \dot{z}_t]^T ,
其中 xt,yt,ztx_t, y_t, z_t 表示潜水器在三维空间中的位置,
x˙t,y˙t,z˙t\dot{x}_t, \dot{y}_t, \dot{z}_t 表示对应的速度。
卡尔曼滤波的预测和更新步骤如下:
. 预测步骤: x →t |t− 1=F →tx→t− 1 |t− 1+B→tu→t \vec{x}_{t |t- 1} = \vec{F}_t \vec{x}_{t- 1 |t- 1} + \vec{B}_t \vec{u}_t P →t |t− 1=F →tP→t− 1 |t− 1F→tT+Q→t \vec{P}_{t |t- 1} = \vec{F}_t \vec{P}_{t- 1 |t- 1} \vec{F}_t^T + \vec{Q}_t
. 更新步骤: K →t=P →t |t− 1H→tT(H→tP→t |t− 1H→tT+R→t)−1 \vec{K}_t = \vec{P}_{t|t- 1} \vec{H}_t^T (\vec{H}_t \vec{P}_{t |t- 1} \vec{H}_t^T + \vec{R}_t)^{- 1} x →t |t=x →t |t− 1+K→t(z →t− H →tx→t |t− 1) \vec{x}_{t |t} = \vec{x}_{t |t- 1} + \vec{K}_t (\vec{z}_t - \vec{H}_t \vec{x}_{t |t- 1}) P→t |t=(I− K →tH→t)P→t |t− 1 \vec{P}_{t |t} = (I - \vec{K}_t \vec{H}_t) \vec{P}_{t |t- 1}
其中, F →t\vec{F}_t 是状态转移矩阵, B →t\vec{B}_t 是控制输入矩阵, u →t\vec{u}_t 是外部控制输入,P →t\vec{P}_t 是估计误差协方差,Q→t\vec{Q}_t 是过程噪声协方差, H →t\vec{H}_t 是观测模型矩阵, R →t\vec{R}_t 是观测噪声协方差, K →t\vec{K}_t 是卡 尔曼增益, z →t\vec{z}_t 是实际观测值。
不确定性分析
. 主要的不确定性来源包括传感器噪声、模型误差、外部环境(如水流变化和海底地形)的未 知性。蒙特卡洛模拟(Monte Carlo Simulation)可用于评估这些不确定性对预测准确性的影 响。
一定要点击文末的卡片,进入后,获取完整论文!!
相关文章:

【高质量精品】2024美赛B题22页word版高质量半成品论文+多版保奖思路+数据+前四问思路代码等(后续会更新)
一定要点击文末的卡片,进入后,获取完整论文!! B 题整体模型构建 1. 潜水器动力系统失效:模型需要考虑潜水器在无推进力情况下的行为。 2. 失去与主船通信:考虑无法从主船接收指令或发送位置信息的情况。…...

apache_exporter安装说明
Apache Exporter 问题描述 需要监控apache服务,部署了apache_exporter,对过程进行一下记录。 源码参见apache_exporter ①下载 https://github.com/Lusitaniae/apache_exporter/releases②解压缩 tar -xzvf apache_exporter-0.7.0.linux-amd64.tar…...

代码随想录算法训练营29期Day42|卡码网46,LeetCode 416
文档讲解:背包问题二维 背包问题一维 分割等和子集 46.整数拆分 题目链接:https://kamacoder.com/problempage.php?pid1046 思路: 在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为d…...
java的excel列行合并模版
1.效果 2.模版 <tableborder"1"cellpadding"0"cellspacing"0"class"tablebor"id"TABLE"><tr align"center" class"bg217"><td style"background-color: #008000; color: #ffffff;p…...
【ES数据可视化】kibana实现数据大屏
目录 1.概述 2.绘制数据大屏 2.1.准备数据 2.2.绘制大屏 3.嵌入项目中 1.概述 再来重新认识一下kibana: Kibana 是一个用于数据可视化和分析的开源工具,是 Elastic Stack(以前称为 ELK Stack)中的一部分,由 Ela…...

2024 年十大 Vue.js UI 库
Vue.js 是一个流行的 JavaScript 框架,它在前端开发者中越来越受欢迎,以其简单、灵活和易用性而闻名。 Vue.js 如此受欢迎的原因之一是它拥有庞大的 UI 库生态系统。 这些库为开发人员提供了预构建的组件和工具,帮助他们快速高效地构建漂亮…...
使用esp32 cam + SR602人体感应模块制作一个小型的监控
需求: 做一个小型的监控,类似电子猫眼,监测到人之后,取一张图 然后发送到自己的邮箱。 架构: 1.sr602 传感器监测到人 2. esp32 cam 取图 并通过mqtt协议传到远端服务器 3, 服务器利用python 搭建一个mqtt客户端&…...

vim最简单命令学习
安装vim sudo apt install vim在终端随便打开一个文本文件,或者源文件, vim filepath输入该命令后,从终端进入vim编辑器,此时为普通模式(Normal)。 按i键进入编辑模式(Insert),按Esc键返回普通模式(Normal)。 在编辑…...

论文阅读-通过云特征增强的深度学习预测云工作负载转折点
论文名称:Cloud Workload Turning Points Prediction via Cloud Feature-Enhanced Deep Learning 摘要 云工作负载转折点要么是代表工作负载压力的局部峰值点,要么是代表资源浪费的局部谷值点。预测这些关键点对于向系统管理者发出警告、采取预防措施以…...

Android Studio从零基础到APP上线(3)
第3章 简单控件 本章介绍App开发常见的几类简单控件的用法,主要包括:显示文字的文本视图,容纳视图的常用布局,响应点击的按钮控件,显示图片的图像视图等。然后结合本章所学的知识,演示一个实战项目“简单计算器”的设计与实现。 3.1 文本显示 本节介绍如何在文本视图Tex…...

springboot Feign方式注入注解详解
一、FeignClient注解详解 FeignClient是Spring Cloud中用于声明Feign客户端的注解,它使得编写HTTP客户端变得更简单。通过Feign的自动化配置机制,可以很容易地编写HTTP API客户端。以下是FeignClient的详解: 作用:FeignClient注解…...
自然语言处理(NLP)—— Dialogflow ES聊天机器人
1. 背景介绍 这个实验室的目标是让你了解并使用Google的Dialogflow服务。Dialogflow是一个可以让你创建聊天机器人的服务,这个过程不需要或者只需要很少的编程技能。 1.1 账号的创建 为了完成这个实验室,你需要在以下网站上创建账号:…...

C++俄罗斯方块 -- 菜单展示和选择 -- 方法
short Menu() //选中开始游戏返回1,离开则返回2 {short choice 1;//跟踪用户选中的选项char c; //记录用户按键信息system("cls");SetPos(9, 12); //设置输出坐标,12行9列cout << "┌────────┐";SetPos(9, 13);cou…...
面试150 颠倒二进制位 位运算分治 逻辑右移
Problem: 190. 颠倒二进制位 文章目录 思路复杂度位运算分治法 思路 👨🏫 参考题解 >>>:逻辑右移(符号位一起移动,高位补零) 复杂度 时间复杂度: O ( log n ) O(\log{n}) O(logn) 空间…...

php 函数三
一 对称加密 1.1 openssl 1.1.1 openssl_get_cipher_methods(bool $aliases false) 获取可用的加密算法。包含可用加密算法的array。 请注意:在 OpenSSL 1.1.1 版本之前,返回加密算法的拼法大小写都有; 从 OpenSSL 1.1.1 开始,…...

Windows下配置多个账号的git ssh
生成密钥 已经有一个密钥的情况下,用下面的命令生成一个新密钥,注意为了防止原始密钥文件被覆盖,需要给一个新名字: ssh-keygen -t rsa -f C:\\Users\\xxx\\.ssh\\id_rsa_xxx -C "xxxemail.com"给GitHub配置SSH Key …...
【漏洞复现】电信网关配置管理系统SQL注入漏洞
Nx01 产品简介 电信网关配置管理系统是一个用于管理和配置电信网络中网关设备的软件系统。它可以帮助网络管理员实现对网关设备的远程监控、配置、升级和故障排除等功能,从而确保网络的正常运行和高效性能。 Nx02 漏洞描述 电信网关配置管理系统存在SQL注入漏洞,攻…...
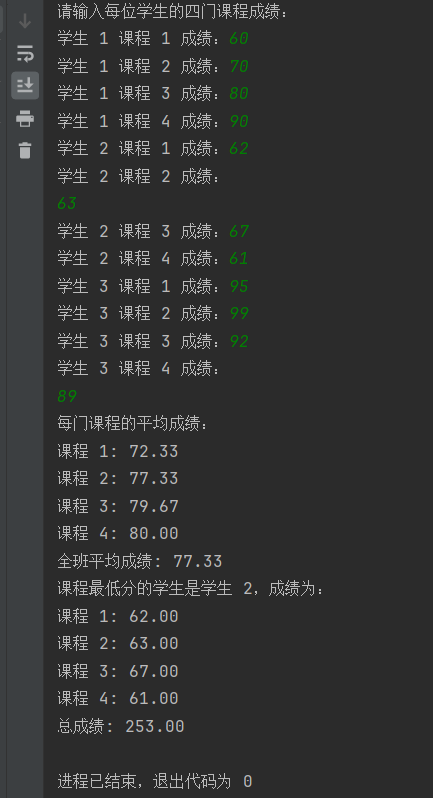
2018年苏州大学837复试机试C/C++
2018年苏州大学复试机试 要求 要求用C/C编程;对程序中必要的地方进行注释。上机规则 请在电脑桌面上新建一个文件夹文件夹名为考试姓名(中文);考试完毕后,将所编写的文件放在上述文件中。 第一题(20分&…...
【Jenkins】pipeline基本使用
目录 一、pipeline 二、创建pipeline项目 1、安装pipeline插件 2、创建pipeline项目 三、pipeline语法 1、pipeline组成 2、agent:指定流水线的执行位置,流水线中每个阶段都必须在某个地方执行 3、stage:阶段,代表流水线的…...

Bytebase 签约 Vianova,助力欧洲城市交通智能平台中 Snowflake 和 PG 的变更自动化及版本控制
在数字化发展的浪潮中,自动化数据库变更管理成为提升产品上线效率、降低人为失误风险的关键工具,同时促进流程的一致性与标准化,确保合规性和变更的可追溯性。近日,数据库 DevOps 团队协同管理工具 Bytebase 签约欧洲交通数据管理…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...
