搜索与图论(一)(深搜,广搜,树与图的存储遍历,拓扑排序)
一、DFS
往深里搜,搜到叶子结点那里,回溯,到可以继续到叶子结点深搜的位置。
1、回溯一定要恢复现场
2、定义一个与当前递归层数有关的终止条件(题目要求的东西)
3、每层都用循环判断是否存在可以dfs的路
输出数字组合
#include<bits/stdc++.h>
//842排列数字 按照字典序将n个数
using namespace std;
const int N=1e5+10;
int path[N];//记录走过的路径
int st[N];//用来记录某个元素是否被用过
int n;
void dfs(int u)
{//先判断是否已经得到一个答案if(u==n){for(int i=0;i<n;i++)cout<<path[i]<<" ";puts("");return;}for(int i=1;i<=n;i++){if(!st[i])//剪枝的过程找到可以构成dfs路径的方向{st[i]=true;path[u]=i;dfs(u+1);path[i]=0;//恢复现场st[i]=false;}}
}
int main()
{cin>>n;dfs(0);return 0;
}
全排列的思想解决n皇后问题,用三个bool数组描述限制条件,用二维char数组保存结果,在恢复现场的时候也要恢复g数组,因为后面的其他结果可能不会将其覆盖掉。
#include<bits/stdc++.h>
//843 n皇后问题(全排列问题)
using namespace std;
const int N=20;
int path[N];//记录走过的路径
char g[N][N];
bool col[N],row[N],dg[N],udg[N];
int n;
void dfs(int u)
{//先判断是否已经得到一个答案if(u==n){for(int i=0;i<n;i++)puts(g[i]);puts("");return;}for(int i=0;i<n;i++){if(!col[i]&&!dg[u+i]&&!udg[n-u+i]){g[u][i]='Q';col[i]=dg[u+i]=udg[n-u+i]=true;dfs(u+1);col[i]=dg[u+i]=udg[n-u+i]=false;g[u][i]='.';}}
}
int main()
{cin>>n;for(int i=0;i<n;i++)for(int j=0;j<n;j++)g[i][j]='.';dfs(0);return 0;
}
按照元素枚举的方式解决n皇后问题
#include<bits/stdc++.h>
//843 n皇后问题(全排列问题)
using namespace std;
const int N=20;
int path[N];//记录走过的路径
char g[N][N];
bool col[N],row[N],dg[N],udg[N];
int n;
void dfs(int x,int y,int u)//x为行,y为列
{if(y==n)y=0,x++;if(x==n){if(u==n)//有可能到头了也没有找到全部的皇后{for(int i=0; i<n; i++)puts(g[i]);puts("");}return;}//为什么要添加xy两个参数//因为这个思路不是循环式地剪枝,是利用递归进行搜索//处理坐标//不放当前位置dfs(x,y+1,u);//放当前位置if(!row[x]&&!col[y]&&!dg[x+y]&&!udg[n-y+x]){g[x][y]='Q';row[x]=col[y]=dg[x+y]=udg[n-y+x]=true;dfs(x,y+1,u+1);g[x][y]='.';row[x]=col[y]=dg[x+y]=udg[n-y+x]=false;}}
int main()
{cin>>n;for(int i=0; i<n; i++)for(int j=0; j<n; j++)g[i][j]='.';dfs(0,0,0);return 0;
}
二、BFS
一层一层地搜索,如果边都是1,bfs第一次搜到的点具有最短路性质

1、具有最短路性质的原因:因为bfs每次都向外扩展一层,依次找到距离起点为1,2,3的所有点。
#include<bits/stdc++.h>
//844走迷宫//添加路径
using namespace std;
const int N=110;
typedef pair<int,int>PII;
int g[N][N];//存图
int d[N][N];//存距离
PII q[N*N];//模拟队列
PII pre[N][N];//路径的前驱
//由于最短路性质,可以直接将当前节点前的一个结点作为前驱
int n,m;void bfs()
{memset(d,-1,sizeof d);//用于判断是否是第一次访问到//一个点可以有多个路径到达,但是第一个到达的一定是最短路d[0][0]=0;int hh=0,tt=0;q[0]={0,0};int dx[4]={-1,0,1,0},dy[4]={0,-1,0,1};while(hh<=tt)//只要非空{auto t=q[hh++];for(int i=0;i<4;i++){int x=t.first+dx[i],y=t.second+dy[i];if(x>=0&&x<n&&y>=0&&y<m&&g[x][y]==0&&d[x][y]==-1){d[x][y]=d[t.first][t.second]+1;q[++tt]={x,y};pre[x][y]=t;}}}int x=n-1,y=m-1;while(x||y){cout<<x<<" "<<y<<endl;x=pre[x][y].first;y=pre[x][y].second;}
}int main()
{cin>>n>>m;for(int i=0; i<n; i++)for(int j=0; j<m; j++)cin>>g[i][j];bfs();cout<<d[n-1][m-1];return 0;
}
三、邻接表邻接矩阵存图
1、邻接表的存法
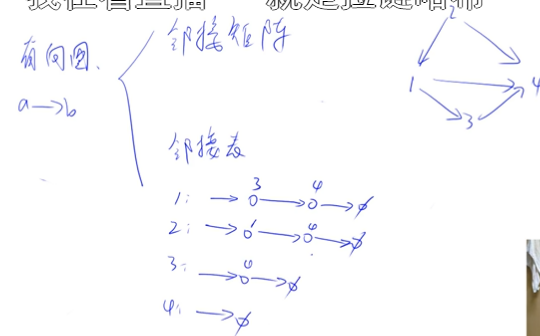
2、使用h数组作为槽,利用e和ne数组和idx构造单链表存槽中相应结点有边相连的节点、
根据题意利用从1深搜,每一层用res存最大的子图的点数,每次计算出一个子连通图添加到sum中。
#include<bits/stdc++.h>
//846 树重心
using namespace std;
const int N=1e5+10,M=N*2;
typedef pair<int,int>PII;
int h[N],e[M],ne[M],idx;
bool st[N];
//h保存n个头结点
//在用数组模拟链表时,e保存链表结点值,ne保存边
//idx让这一切有序
int ans=N,n;//存结果
int dfs(int u)//u是结点的名字不是idx性质的
{st[u]=true;//标记这个结点已经被搜索过了//在遍历当前节点的所有子树之前int sum=1;//存所有子树的节点个数int res=0;//记录各个连通子图的节点个数for(int i=h[u];i!=-1;i=ne[i]){int j =e[i];if(st[j]==false)//只要这个结点的子树还没计算{int t=dfs(j);res=max(res,t);//存最大连通子图sum+=t;//所有子树}}res=max(res,n-sum);ans=min(ans,res);//保存最小的最大连通子图return sum;}void add(int a,int b)//头插法
{e[idx]=b;//每个idx都代表一个链表上的节点ne[idx]=h[a];h[a]=idx++;
}int main()
{memset(h,-1,sizeof h);//memset(st,false,sizeof st);//所有结点的单链表指向的位置都为空cin>>n;for(int i=0;i<n-1;i++){int a,b;cin>>a>>b;add(a,b),add(b,a);}dfs(1);cout<<ans<<endl;}3、邻接表利用bfs计算最短路
#include<bits/stdc++.h>
//847图中点的层次
using namespace std;
const int N=1e5+10,M=2*N;
int n,m;
int h[N],e[N],ne[N],idx;
int d[N],q[N];
void add(int a,int b)
{e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int bfs()
{int hh=0,tt=0;memset(d,-1,sizeof d);q[0]=1;//1是结点的名字,入队d[1]=0;//到第一个结点的距离为0//数组模拟队列的时候hh永远指向队列的第一个元素,tt永远指向队尾,所以判断队列不为空的判断条件是hh<=tt。while(hh<=tt){int t=q[hh++];//拿出队头元素for(int i=h[t];i!=-1;i=ne[i])//遍历与其相连的所有边{int j=e[i];//if(d[j]==-1){d[j]=d[t]+1;q[++tt]=j;}}}return d[n];
}
int main()
{cin>>n>>m;memset(h,-1,sizeof h);for(int i=0;i<m;i++){int a,b;cin>>a>>b;add(a,b);}cout<<bfs()<<endl;return 0;
}
4、有向无环图一定有拓扑序列,拓扑排序的实现
#include<bits/stdc++.h>
//848拓扑排序
using namespace std;
const int N=1e5+10,M=2*N;
int n,m;
int h[N],e[N],ne[N],idx;
int d[N],q[N];void add(int a,int b)
{e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}bool topsort()
{int hh=0,tt=-1;for(int i=1;i<=n;i++){if(!d[i])q[++tt]=i;}while(hh<=tt){int t=q[hh++];for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];d[j]--;if(!d[j])q[++tt]=j;}}return tt==n-1;
}int main()
{cin>>n>>m;memset(h,-1,sizeof h);for(int i=0;i<m;i++){int a,b;cin>>a>>b;add(a,b);d[b]++;}if(!topsort())puts("-1");else{for(int i=0;i<n;i++)cout<<q[i]<<" ";puts("");}
}
相关文章:

搜索与图论(一)(深搜,广搜,树与图的存储遍历,拓扑排序)
一、DFS 往深里搜,搜到叶子结点那里,回溯,到可以继续到叶子结点深搜的位置。 1、回溯一定要恢复现场 2、定义一个与当前递归层数有关的终止条件(题目要求的东西) 3、每层都用循环判断是否存在可以dfs的路 输出数字…...

【开源】基于JAVA+Vue+SpringBoot的停车场收费系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 停车位模块2.2 车辆模块2.3 停车收费模块2.4 IC卡模块2.5 IC卡挂失模块 三、系统设计3.1 用例设计3.2 数据库设计3.2.1 停车场表3.2.2 车辆表3.2.3 停车收费表3.2.4 IC 卡表3.2.5 IC 卡挂失表 四、系统实现五、核心代码…...
DDoS攻击激增,分享高效可靠的DDoS防御方案
当下DDoS攻击规模不断突破上限,形成了 "网络威胁格局中令人不安的趋势"。专业数据显示,对比2022年上半年与2023年上半年,所有行业的DDoS攻击频率增加了314%。其中零售、电信和媒体公司遭受的攻击规模最大,三个垂直行业的…...

打卡今天学习的命令 (linux
1.1 cp - 复制文件或目录 cp source destination cp -r source_directory destination # 递归复制目录及其内容1.2 rm - 删除文件或目录 rm file rm -r directory # 递归删除目录及其内容1.3 mv - 移动/重命名文件或目录 mv source destination mv old_name new_name # 重…...

[C#]无法获取源 https://api.nuge t.org/v3-index存储签名信息解决方法
参考网上大部分方法错误,根本不起作用。正确方法是 C:\Users\你的用户名\AppData\Roaming\NuGet找到NuGet.Config打开,看到类似下面信息(可能不一样) <?xml version"1.0" encoding"utf-8"?> <co…...

FRP内网穿透如何避免SSH暴力破解(二)——指定地区允许访问
背景 上篇文章说到,出现了试图反复通过FRP的隧道,建立外网端口到内网服务器TCP链路的机器人,同时试图暴力破解ssh。这些连接造成了流量的浪费和不必要的通信开销。考虑到服务器使用者主要分布在A、B、C地区和国家,我打算对上一篇…...

Unity类银河恶魔城学习记录4-1,4-2 Attack Logic,Collider‘s collision excepetion源代码 P54 p55
Alex教程每一P的教程原代码加上我自己的理解初步理解写的注释,可供学习Alex教程的人参考 此代码仅为较上一P有所改变的代码【Unity教程】从0编程制作类银河恶魔城游戏_哔哩哔哩_bilibili Entity.cs using System.Collections; using System.Collections.Generic; u…...

各种编程语言送祝福:2024龙年大吉
我是码农一枚,在这里用不同编程语言中祝福大家"2024,龙年大吉"~ Python print("2024,龙年大吉")Java public class Main {public static void main(String[] args) {System.out.println("2024,龙年大…...

C++中用Boost::Python调用Python模块
这个过程有挺多坑,记录一下。我这里的环境: Windows 11 Qt 6.2 Boost 1.8.4 CMake 3.25.2 Visual Stutio 2019(主要用于C编译) 1、下载并将Boost编译为静态库 b2.exe toolsetmsvc-14.2 install --prefixboost安装路径 links…...
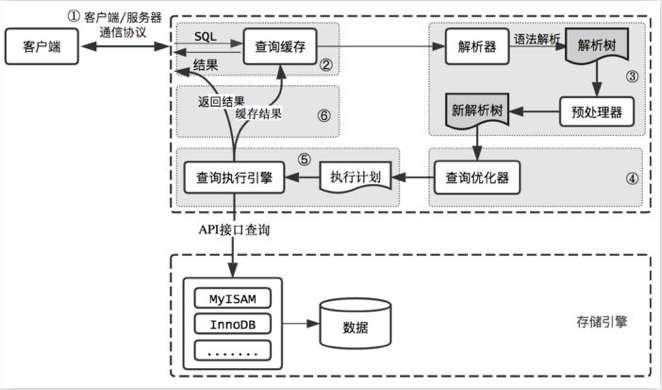
MySQL查询缓存
MySQL查询缓存 MySQL在查询的时候首先会查询缓存,如果缓存命中的话就直接返回结果,不需要解析sql语句,也不会生成执行计划,更不会执行;如果没有命中缓存,则再进行SQL解析以及进行查询,并将结果返…...

Filter 实现过滤符合条件的请求并落库
其他系列文章导航 Java基础合集数据结构与算法合集 设计模式合集 多线程合集 分布式合集 ES合集 文章目录 其他系列文章导航 文章目录 前言 一、配置过滤器类 二、定义数据表、实体类、Mapper 2.1 DDL 2.2 实体类 2.3 Mapper 三、创建一个过滤器 四、实现 Nacos 配置…...

使用ChatGpt和文心一言辅助文章创作
近期在写数字水浒系列文章,使用了ChatGpt和文心一言进行辅助创作,整体感受不错,提高了工作效率。 在使用过程中,感觉文心的中文能力更强一些,主要体现在: 1 语料库更大,比如对水浒传了解的更多…...

OpenCV识别视频中物体运动并截取保存
功能很简单:输入原始视频,输出视频中有画面变化的部分 适合理解基本框架,可以在这个基础上增加各种酷炫时髦的功能 [doge] ※注释非常保姆级※ import cv2 import numpy as np import os from datetime import datetime# 检测两帧之间变化…...

6.Swift字面量
Swift 字面量 在 Swift 中,字面量是指直接指定数值、字符串、布尔值等常量的值的表示方式。使用字面量可以直接在代码中指定常量的值,而不需要通过变量或常量来存储。Swift 支持多种类型的字面量,包括整数、浮点数、布尔值、字符串、数组、字…...

拿捏循环链表
目录: 一:单链表(不带头单向不循环)与循环链表(带头双向循环)区别 二:循环链表初始化 三:循环链表头插 四:循环链表尾插 五:循环链表头删 六࿱…...
)
UMLChina公众号精选(20240207更新)
UMLChina服务 如何选择UMLChina服务 《软件方法》分步改进指南 做对《软件方法》强化自测题获得“软件方法建模师”称号 建模示范视频 [EA-029/石油钻井管理平台]35套UML/SysMLEA/StarUML的建模示范视频-全程字幕 UMLChina连EA经销商都不是,EA水平靠谱嘛?…...

东南亚手游市场攻略:出海前的关键准备与注意事项
随着全球游戏市场的日益繁荣,越来越多的手游企业开始将目光投向海外市场,其中东南亚地区因其庞大的用户基数和逐渐成熟的游戏市场环境,成为了不少企业的首选目标。然而,想要在东南亚市场取得成功,并非易事。本文Nox聚星…...
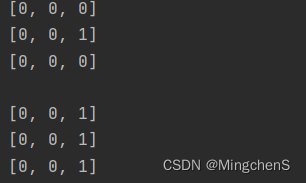
python二维数组初始化的一个极其隐蔽的bug(浅拷贝)
初始化一个三行三列的矩阵 m n 3初始化方式1 a [[0 for i in range(m)] for j in range(n)]初始化方式2 b [] row [0 for i in range(0,m)] for i in range(0,n):b.append(row)分别输出两个初始化的结果 for row in a:print(row) for row in b:print(row)当前的输出为…...
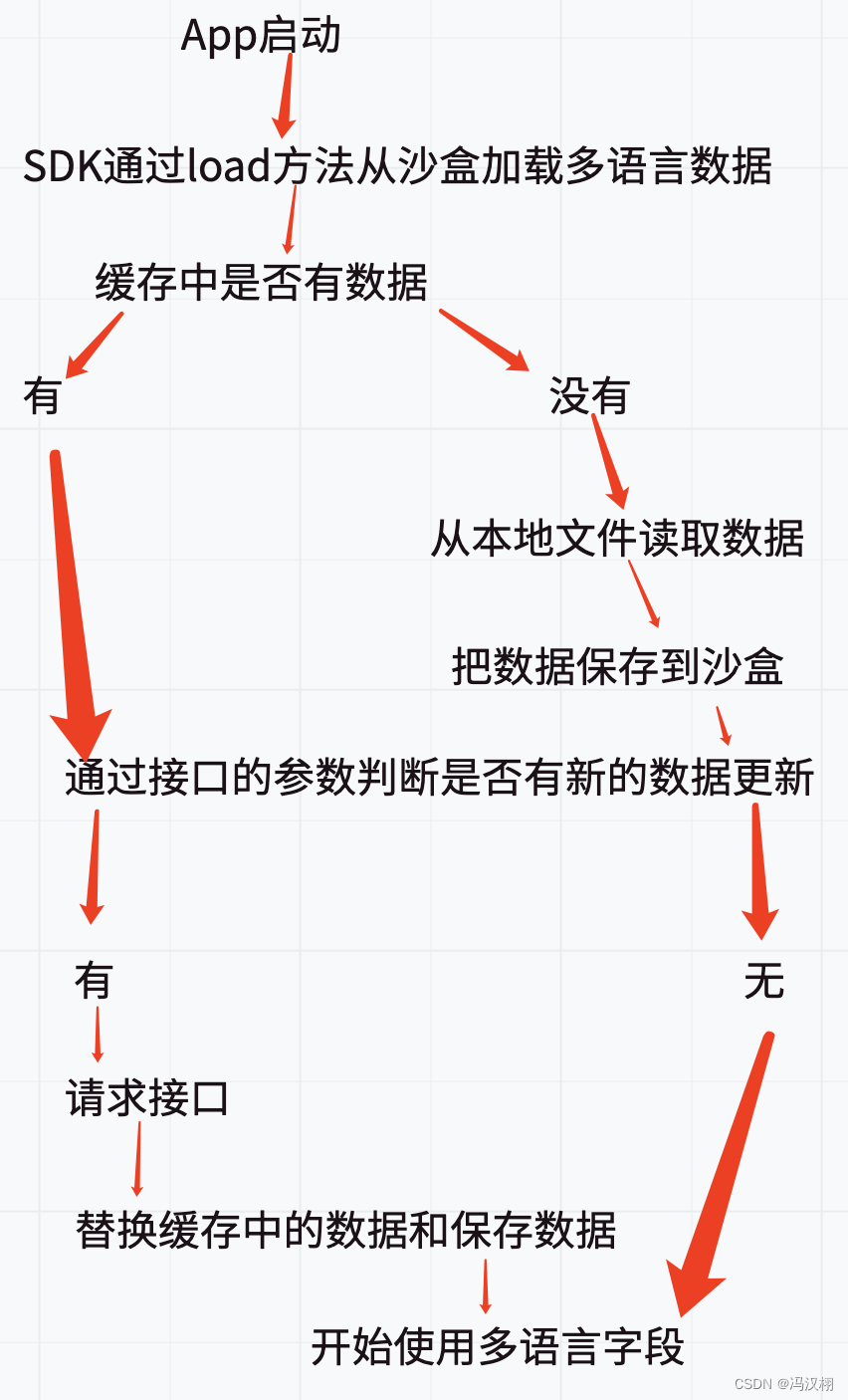
iOS 需求 多语言(国际化)App开发 源码
一直觉得自己写的不是技术,而是情怀,一个个的教程是自己这一路走来的痕迹。靠专业技能的成功是最具可复制性的,希望我的这条路能让你们少走弯路,希望我能帮你们抹去知识的蒙尘,希望我能帮你们理清知识的脉络࿰…...
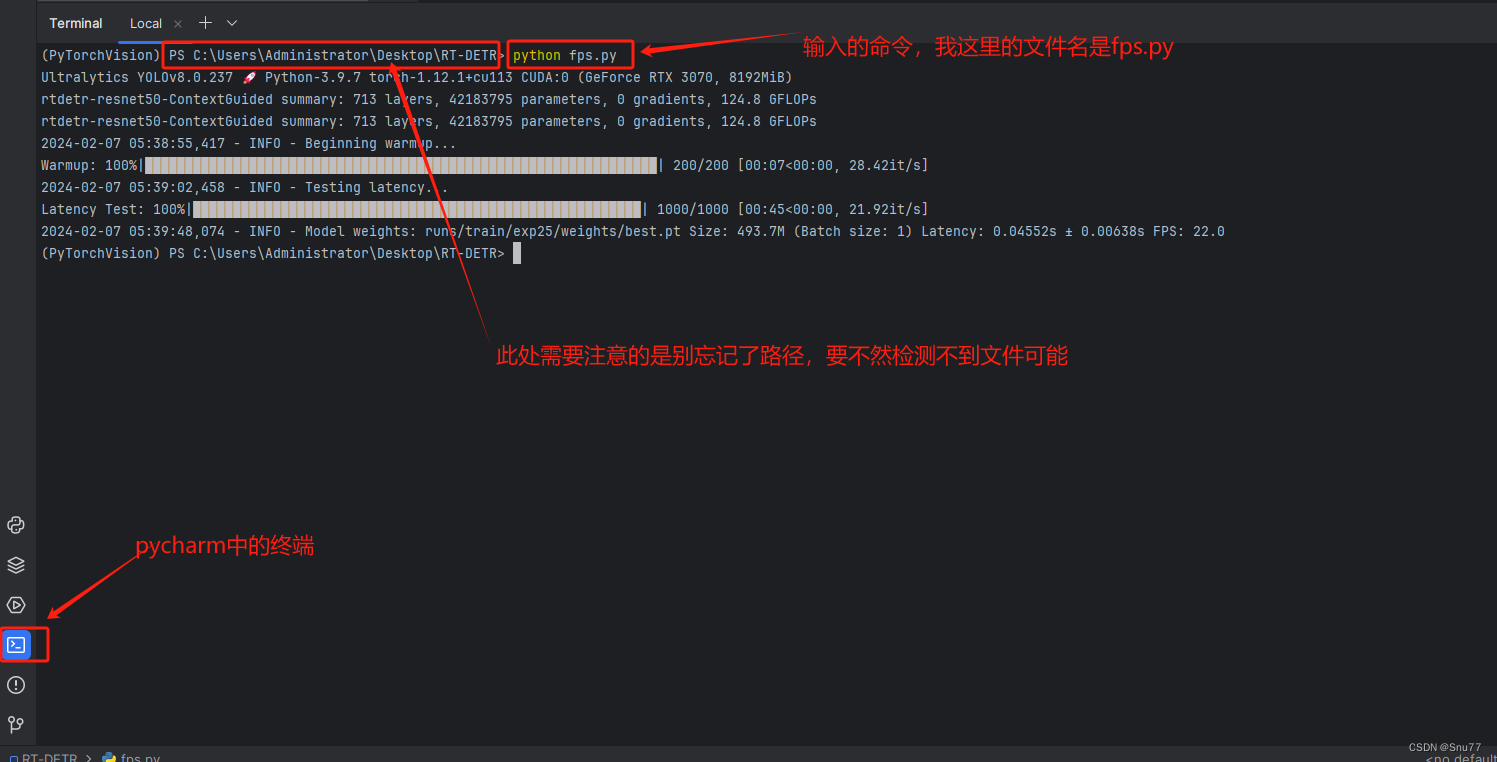
YOLOv8改进 | 利用训练好权重文件计算YOLOv8的FPS、推理每张图片的平均时间(科研必备)
一、本文介绍 本文给大家带来的改进机制是利用我们训练好的权重文件计算FPS,同时打印每张图片所利用的平均时间,模型大小(以MB为单位),同时支持batch_size功能的选择,对于轻量化模型的读者来说,本文的内容对你一定有帮助,可以清晰帮你展示出模型速度性能的提升以及轻量…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
