特征工程:特征提取和降维-上
目录
一、前言
二、正文
Ⅰ.主成分分析
Ⅱ.核主成分分析
三、结语
一、前言
前面介绍的特征选择方法获得的特征,是从原始数据中抽取出来的,并没有对数据进行变换。而特征提取和降维,则是对原始数据的特征进行相应的数据变换,并且通常会选择比原始特征数量少的特征,同时达到数据降维的目的。常用的数据特征提取和降维的方法有主成分分析,核成分分析,流行学习,t-SNE,多维尺度分析等方法。
二、正文
from sklearn.decomposition import PCA,KernelPCA
from sklearn.manifold import Isomap,MDS,TSNE
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_wine
wine_x,wine_y=load_wine(return_X_y=True)
wine_x=StandardScaler().fit_transform(wine_x)
在介绍特征提取和降维的方法之前,我们先导包读取相应的数据。 通过标准化进行数据特征变换的处理。
Ⅰ.主成分分析
pca=PCA(n_components=13,random_state=123)
pca.fit(wine_x)
exvar=pca.explained_variance_
plt.figure(figsize=(10,6))
plt.plot(exvar,'r-o')
plt.hlines(y=1,xmin=0,xmax=12)
plt.xlabel('number')
plt.ylabel('PCA')
plt.show()
主成分分析法(Principal Component Analysis,PCA)是采用一种数学降维的方法,在损失很少信息的前提下,找出几个综合变量为主成分,来代替原来众多的变量,使这些主成分尽可能地代表原始数据的信息,其中每个主成分都是原始变量的线性组合,而且各个主成分之间不相关(即线性无关)。通过主成分分析,我们可以从事物错综复杂的关系中找到一些主要成分(通常选择累积 贡献率≥85%的前m个主成分),从而能够有效利用大量统计信息进行定性分析,揭示变量之间的内在关系,得要一些事物特征及其发展规律的深层次信息和启发,推动研究进一步深入。通常使用主成分个数远小于原始特征个数,使用起到特征提取和降维的目的。
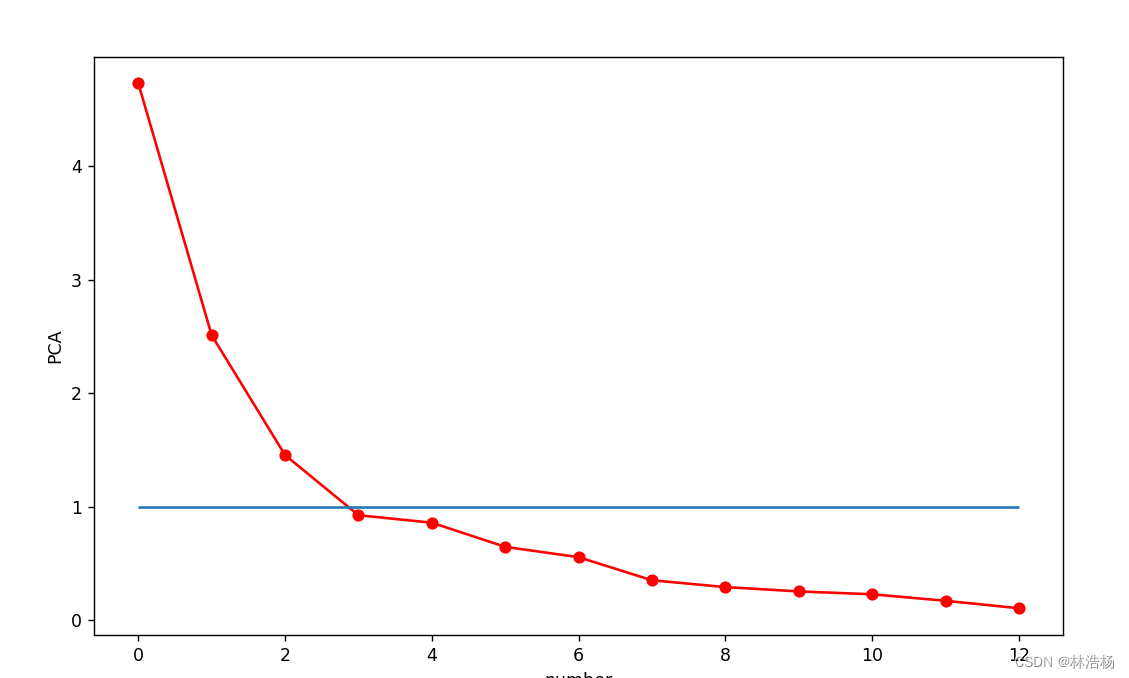
从结果分析,使用数据的前三个主成分即可对其进行良好的数据建模。
pca_wine_x=pca.transform(wine_x)[:,0:3]
print(pca_wine_x.shape)
#输出结果
(178,3)
如上我们可以知道,前三个主成分可对其数据建模,于是我们pca进行数据变换之后对其进行切片,前三列的数据。
colors=['red','blue','green']
shape=['o','s','*']
fig=plt.figure(figsize=(10,6))
ax1=fig.add_subplot(111,projection='3d')
for ii,y in enumerate(wine_y):ax1.scatter(pca_wine_x[ii,0],pca_wine_x[ii,1],pca_wine_x[ii,2],s=40,c=colors[y],marker=shape[y])ax1.set_xlabel('pca1',rotation=20)
ax1.set_ylabel('pca2',rotation=20)
ax1.set_zlabel('pca3',rotation=20)
ax1.azim=225
ax1.set_title('pca')
plt.show()
先将三种成分分别的颜色和标记封装在列表当中,然后设置窗口, 111是设置位置即第一行第一列的第一个格子,则会也就意味着这里只有一个图,projection(映射)参数设置为3d,然后将前三个主成分通过循环在三维空间画出其数据分布。
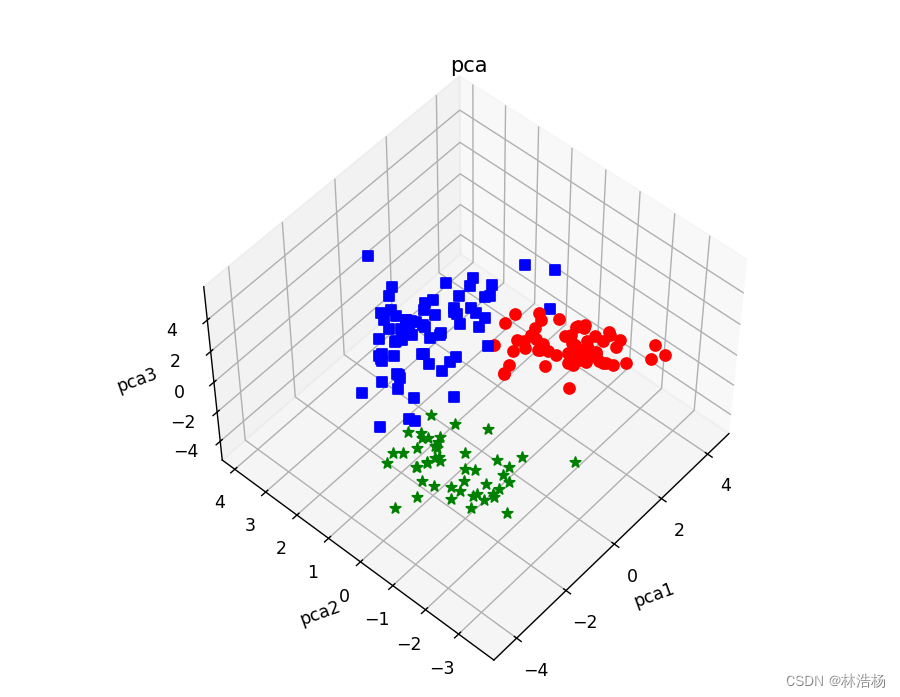
这样我们就能区分出三个主成分的数据分布情况,即不同类别的分布情况。
Ⅱ.核主成分分析
PCA是线性的数据降维技术,而核主成分分析则是针对非线性的数据表示,对其进行特征提取并数据降维。
kpca=KernelPCA(n_components=13,kernel='rbf',gamma=0.2,random_state=123)
kpca.fit(wine_x)
eigenvalues=kpca.eigenvalues_
plt.figure(figsize=(10,6))
plt.plot(eigenvalues,'r-o')
plt.hlines(y=4,xmin=0,xmax=12)
plt.xlabel('number')
plt.ylabel('KernelPCA')
plt.show()
方法与主成分分析大差不大,但是这里注意一个KernelPCA类中的一个属性:
eigenvalues_:Eigenvalues of the centered kernel matrix in decreasing order. If
n_componentsandremove_zero_eigare not set, then all values are stored.
翻译过来就是:中心核向量的特征值按照降序排序,如果未设置n_components和remove_zero_eig,则存储所有值。
原本这个属性叫做lambdas_,但是被更改为eigenvalues_(特征值)。

同样针对前三个核主成分,可以在三维空间将数据分布进行可视化。
kpca_wine_x=kpca.transform(wine_x)[:,0:3]
print(kpca_wine_x.shape)
colors=['red','blue','green']
shape=['o','s','*']
fig=plt.figure(figsize=(10,6))
ax1=fig.add_subplot(111,projection='3d')
for ii,y in enumerate(wine_y):ax1.scatter(kpca_wine_x[ii,0],kpca_wine_x[ii,1],kpca_wine_x[ii,2],s=40,c=colors[y],marker=shape[y])ax1.set_xlabel('kpca1',rotation=20)
ax1.set_ylabel('kpca2',rotation=20)
ax1.set_zlabel('kpca3',rotation=20)
ax1.azim=225
ax1.set_title('kpca')
plt.show()
做法跟主成分大差不差,利用散点在空间中的分布来发现其中的数据分布情况。
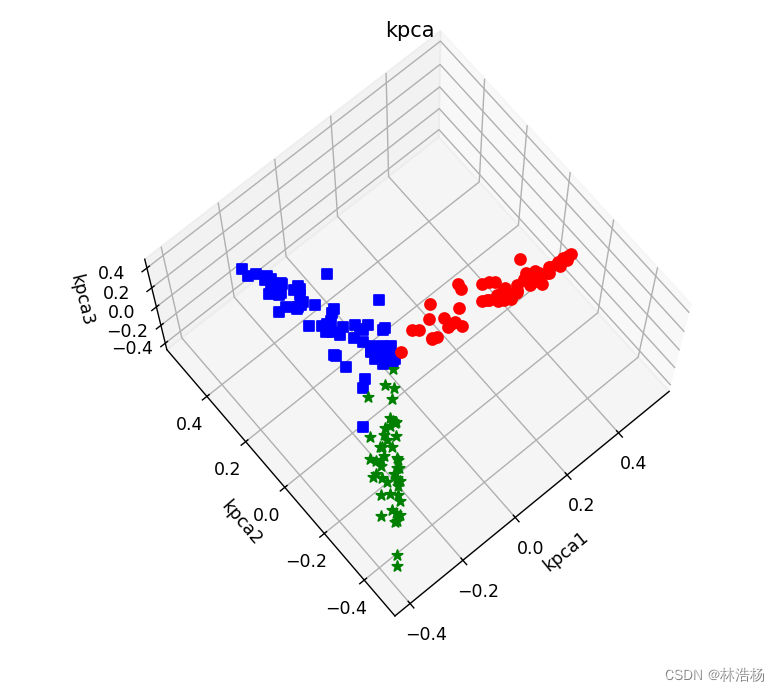
可以看出核主成分分析与主成分分析之间的主成分核成分之间的数据分布情况大有不同。
三、结语
上篇我们先从线性与非线性入手,希望能对你提供帮助,点赞收藏以备不时之需,关注我,有关新的数据分析的文章第一时间告知于你
相关文章:

特征工程:特征提取和降维-上
目录 一、前言 二、正文 Ⅰ.主成分分析 Ⅱ.核主成分分析 三、结语 一、前言 前面介绍的特征选择方法获得的特征,是从原始数据中抽取出来的,并没有对数据进行变换。而特征提取和降维,则是对原始数据的特征进行相应的数据变换,并…...

前端JavaScript篇之强类型语言和弱类型语言的区别和对比
目录 强类型语言和弱类型语言的区别和对比总结 强类型语言和弱类型语言的区别和对比 强类型语言和弱类型语言是编程语言的两种不同类型系统,它们处理变量类型的方式有所不同。 强类型语言: 强类型语言要求在使用变量之前必须明确声明其类型,…...
[红日靶机渗透] ATKCK红队评估实战靶场三
🍬 博主介绍👨🎓 博主介绍:大家好,我是 hacker-routing ,很高兴认识大家~ ✨主攻领域:【渗透领域】【应急响应】 【ATK&CK红队评估实战靶场】 【VulnHub靶场复现】【面试分析】 …...
)
网课:N皇后问题——牛客(题解和疑问)
题目描述 给出一个nnn\times nnn的国际象棋棋盘,你需要在棋盘中摆放nnn个皇后,使得任意两个皇后之间不能互相攻击。具体来说,不能存在两个皇后位于同一行、同一列,或者同一对角线。请问共有多少种摆放方式满足条件。 输入描述: …...
[大厂实践] Netflix容器平台内核panic可观察性实践
在某些情况下,K8S节点和Pod会因为出错自动消失,很难追溯原因,其中一种情况就是发生了内核panic。本文介绍了Netflix容器平台针对内核panic所做的可观测性增强,使得发生内核panic的时候,能够导出信息,帮助排…...

2024/2/8
数据类型与作用域练习 1、选择题 1.1、以下选项中,不能作为合法常量的是 ___b_______ A)1.234e04 B)1.234e0.4 C)1.234e4 D)1.234e0 1.2、以下定义变量并初始化错误的是______d_______。 A) char c1 ‘H’ &am…...
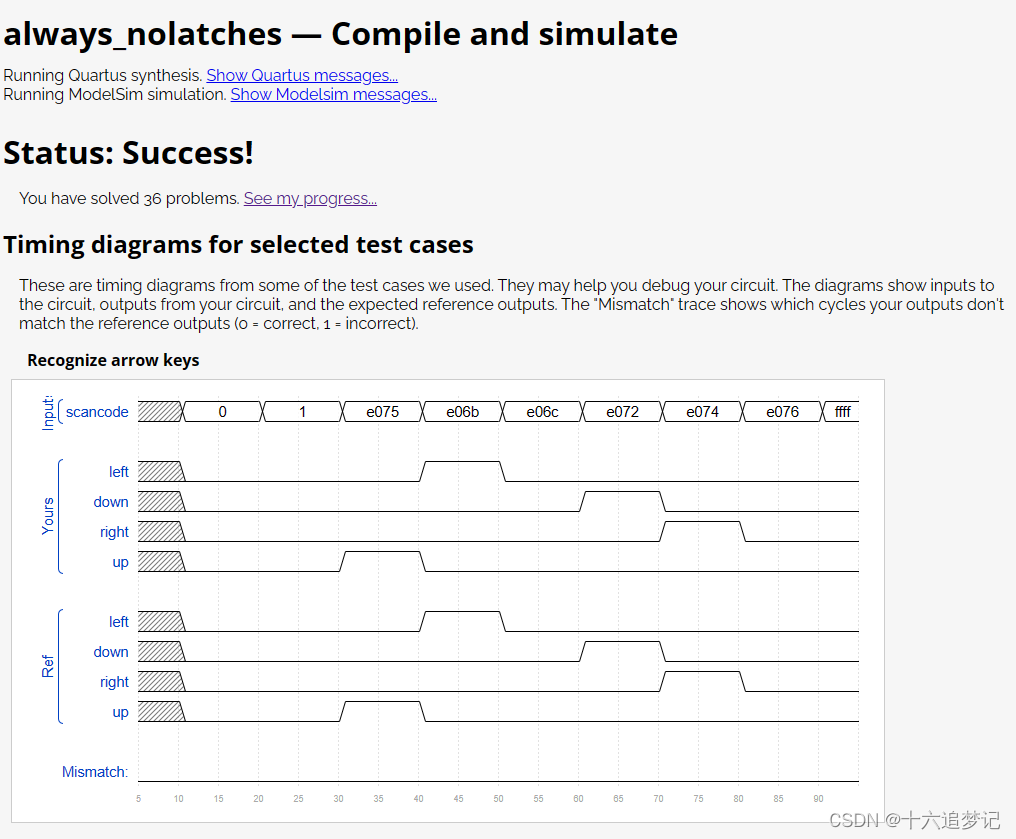
Verilog刷题笔记23
题目: Suppose you’re building a circuit to process scancodes from a PS/2 keyboard for a game. Given the last two bytes of scancodes received, you need to indicate whether one of the arrow keys on the keyboard have been pressed. This involves a fairly simp…...
C#验证字符串的长度,用正则表达式 vs 字符数组长度或字符串的长度
目录 一、使用的方法 1.使用正则表达式 2.通过计算字符串的长度验证 二、实例 1.源码 2.生成效果 一、使用的方法 1.使用正则表达式 使用正则表达式可以判断和限制用户输入的字符串长度。 比如验证用户密码不得少于8为,匹配的正则表达式"^.{8,}$"…...

opencv C++ dnn模块调用yolov5以及Intel RealSense D435深度相机联合使用进行目标检测
一、代码 #include <opencv2/opencv.hpp> #include <opencv2/dnn/dnn.hpp> #include <librealsense2/rs.hpp> // Include RealSense Cross Platform APIusing namespace cv; using namespace dnn; using namespace std; using namespace rs2;// 类名数组&am…...
2024牛客寒假算法基础集训营1(视频讲解全部题目)
2024牛客寒假算法基础集训营1(题目全解) ABCDEFGHIJKLM 2024牛客寒假算法基础集训营1(视频讲解全部题目) A #include<bits/stdc.h> #define endl \n #define deb(x) cout << #x << " " << …...

第三百一十三回
文章目录 1. 概念介绍2. 实现方法2.1 obscureText属性2.2 decoration属性 3. 示例代码4. 内容总结 我们在上一章回中介绍了"如何实现倒计时功能"相关的内容,本章回中将介绍如何实现密码输入框.闲话休提,让我们一起Talk Flutter吧。 1. 概念介绍…...
倒计时61天
M-智乃的36倍数(normal version)_2024牛客寒假算法基础集训营3 (nowcoder.com) //非ac代码,超时了,54.17/100#include<bits/stdc.h> using namespace std; const int N1e55; const int inf0x3f3f3f3f; #define int long long int n; string s1[N]; void solve() {cin>…...
)
npm后Truffle找不到命令(ubantu20系统)
Truffle找不到命令 方法1方法2 方法1 # 编辑.profile vim ~/.profile # 在.profile末尾把nodejs的解压路径添加到$PATH环境变量中 PATH"$HOME/bin:$HOME/.local/bin:路径:$PATH" source 文件方法2 #ls -l 在nodejs的bin目录下查看truffle链接的脚本文件 truffle -&…...
嵌入式学习第三篇——51单片机
目录 1,嵌入式系统 1,嵌入式系统的定义 2,单片机的定义 2,51单片机 1,开发环境 2,开发板使用的基本思路 1,查看原理图,查看芯片手册 2,获得调用硬件的管…...
RabbitMQ详解
RabbitMQ 1.初识MQ 1.1.同步和异步通讯 微服务间通讯有同步和异步两种方式: 同步通讯:就像打电话,需要实时响应。 异步通讯:就像发邮件,不需要马上回复。 两种方式各有优劣,打电话可以立即得到响应&a…...

CGAL::2D Arrangements-4
4. Free函数 Arrangement_on_surface_2类模板是用曲线切分二维的面。因为它的接口设计是最简化的,这意味着它的成员函数很少执行几何操作。本章将解释怎么利用这些Free function来达到Arrangement操作。执行这些操作通常需要优秀的几何算法,而且有时会对…...
终端命令提示符:如何查看我们电脑端口是否被占用和处理方式
文章目录 端口信息查看1、Windows:2、Linux/macOS: 使用 netstat使用 lsof 端口信息查看 在不同的操作系统中,查看端口是否被占用的指令有所不同。以下是一些常见的指令: 1、Windows: 使用命令行工具 netstat 来查看端口占用情况。 电脑键盘按住 win…...
elasticsearch重置密码操作
安装es的时候需要测试这个url:http://127.0.0.1:9200/ 出现弹窗让我输入账号和密码。我第一次登录,没有设置过账号和密码, 解决方法是:在es的bin目录下打开cmd窗口,敲命令:.\elasticsearch-reset-password…...
—— 导航)
从零开始手写mmo游戏从框架到爆炸(零)—— 导航
从今天开始我们尝试从零开始写一个mmo的游戏。主要技术还是netty。参考了网上很多的大神的框架,本来希望基于ioGame或者vert.x等来直接写功能的,觉得从零开始更有意义,而且咱们也不需要太NB的底层功能,够用就行。 下面是导航&…...
)
机器学习7-K-近邻算法(K-NN)
K-Nearest Neighbors(K-近邻算法,简称KNN)是一种基本的监督学习算法,用于解决分类和回归问题。KNN的核心思想是基于距离度量,在特征空间中找到最近的K个样本,然后使用它们的标签进行决策。以下是KNN的基本概…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...
