彻底学会系列:一、机器学习之线性回归(一)
1.基本概念(basic concept)
线性回归: 有监督学习的一种算法。主要关注多个因变量和一个目标变量之间的关系。
因变量: 影响目标变量的因素: X 1 , X 2 . . . X_1, X_2... X1,X2... ,连续值或离散值。
目标变量: 需要预测的值: t a r g e t target target, y y y
因变量和目标变量之间的关系: 即模型,model
1.1连续值(continuous value)
连续值是可以在一个区间范围内取任意值的变量。例如,身高、体重、温度、时间等都是连续值

1.2离散值(discrete value)
离散值是只能取有限个数值或者可数值的变量。例如,学生人数、家庭成员数、考试分数等都是离散值

1.3简单线性回归(simple linear regression)
简单线性回归对应的公式: y = w x + b y = wx + b y=wx+b
y y y 是目标变量即未来要预测的值
x x x 是影响 y y y 的因素
w , b w,b w,b 是公式上的参数即要求的模型, w w w就是斜率, b b b就是截距
一元一次方程:
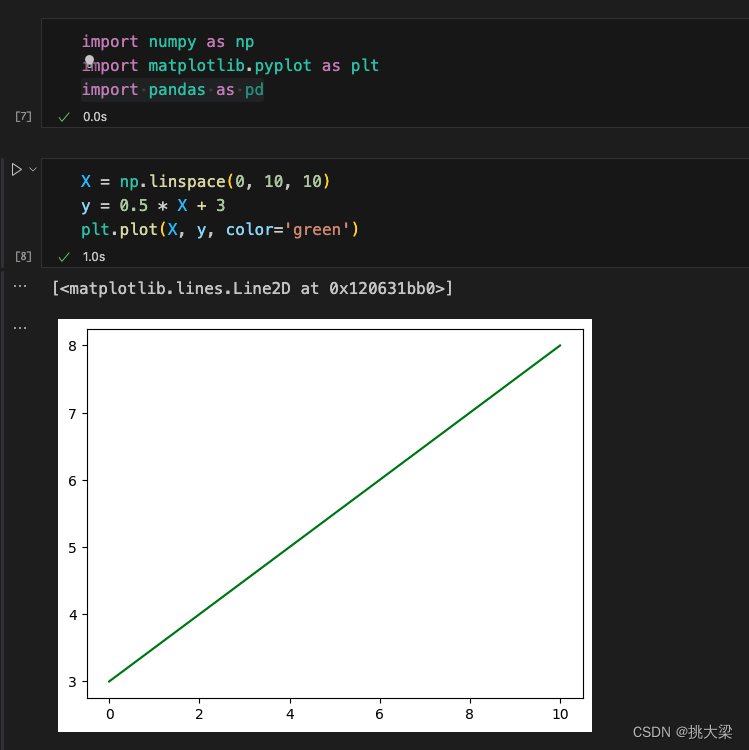
一元二次方程:
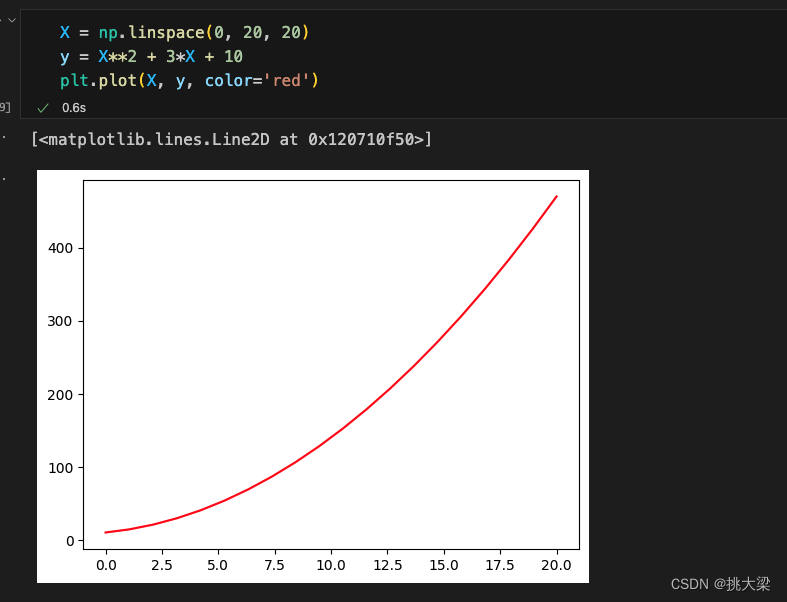
1.4多元线性回归(multiple linear regression)
现实生活中,往往影响结果 y 的因素不止一个,有可能是 n 个, X 1 , X 2 , X n . . . X_1,X_2,X_n... X1,X2,Xn...
多元线性回归公式:
y ^ = w 1 X 1 + w 2 X 2 . . . w n X n + b \hat y = w_1X_1 + w_2X_2 ... w_nX_n + b y^=w1X1+w2X2...wnXn+b
b是截距,也可以表示成:
y ^ = w 1 X 1 + w 2 X 2 . . . w n X n + w 0 \hat y = w_1X_1 + w_2X_2 ... w_nX_n + w_0 y^=w1X1+w2X2...wnXn+w0
使用向量来表示:
y ^ = W T X \hat y = W^TX y^=WTX
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression# 转化矩阵
x1 = np.random.randint(-150, 150, size=(300, 1))
x2 = np.random.randint(0, 300, size=(300, 1))# 斜率和截距,随机生成
w = np.random.randint(1, 5, size=2)
b = np.random.randint(1, 10, size=1)# 根据二元一次方程计算目标值y,并加上"噪声"
y = x1 * w[0] + x2 * w[1] + b + np.random.randn(300, 1)
fig = plt.figure(figsize=(9, 6))
ax = plt.subplot(111, projection='3d')
ax.scatter(x1, x2, y) # 三维散点图
ax.view_init(elev=10, azim=-20) # 调整视角
#
X = np.concatenate([x1, x2], axis=1)
model = LinearRegression()
model.fit(X, y)
w_ = model.coef_.reshape(-1)
b_ = model.intercept_print('一元一次方程真实的斜率和截距是:\n', w, b)
print('通过scikit-learn求解的斜率和截距是:\n', w_, b_)x = np.linspace(-150, 150, 100)
y = np.linspace(0, 300, 100)
z = x * w_[0] + y * w_[1] + b_
ax.plot(x, y, z, color='green')plt.show()
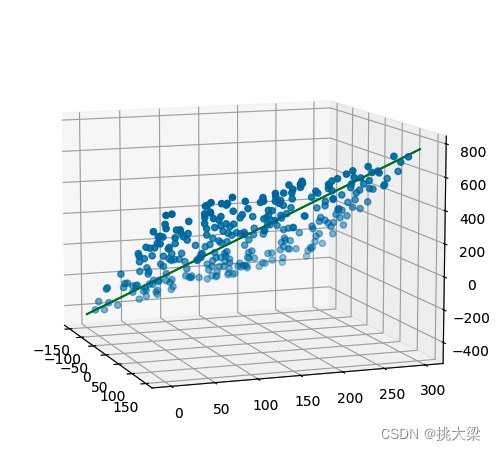
1.5 最优解(optimal solution)
y y y: 真实值(actual value)
y ^ \hat y y^: 预测值(predicted value), 根据因变量 X 1 , X 2 . . . X_1,X_2... X1,X2...和计算出来的参数w,b得到
e r r o r error error: 误差,预测值和真实值的差距( ε \varepsilon ε)
最优解: 尽可能的找到一个模型使得整体的误差最小,通常叫做损失 Loss,通过损失函数Loss Function计算得到。
from sklearn.linear_model import LinearRegressionX = np.linspace(0, 10, num=30).reshape(-1, 1)
w = np.random.randint(1, 5, size=1)
b = np.random.randint(1, 10, size=1)y = X * w + b + np.random.randn(30, 1)
plt.scatter(X, y)model = LinearRegression()
model.fit(X, y)
w_ = model.coef_
b_ = model.intercept_print('一元一次方程真实的斜率和截距是:\n', w, b)
print('通过scikit-learn求解的斜率和截距是:\n', w_, b_)plt.plot(X, X.dot(w_) + b_, color='green')
plt.show()
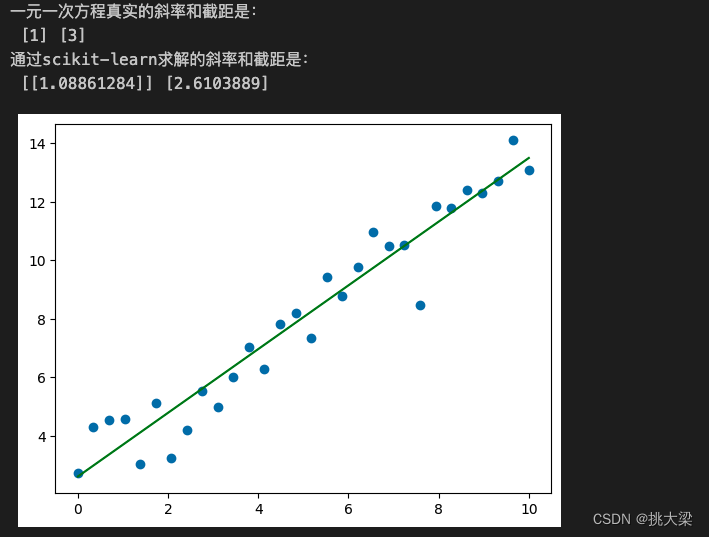
1.6 高斯密度函数 (Gaussian Density Function):
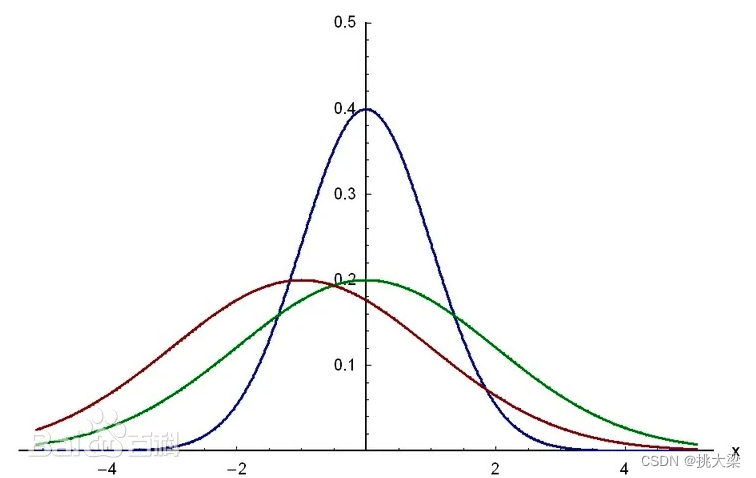
高斯密度函数(Gaussian Density Function)也被称为正态分布或钟形曲线,是统计学中最常用的概率分布之一。其概率密度函数(Probability Density Function, PDF)的表达式如下:
f ( x ; μ , σ 2 ) = 1 2 π σ exp ( − ( x − μ ) 2 2 σ 2 ) \ f(x; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi}\sigma} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) f(x;μ,σ2)=2πσ1exp(−2σ2(x−μ)2)
其中,(x) 是变量, μ \mu μ 是均值, σ 2 \sigma^2 σ2是方差。
- μ \mu μ 表示分布的均值,决定了曲线的中心位置。
- σ 2 \sigma^2 σ2 是方差,决定了曲线的宽度或分布的离散程度。标准差 σ \sigma σ是方差的平方根。
高斯密度函数的特征包括:
-
钟形曲线形状: 高斯分布呈现出典型的钟形曲线,对称分布在均值周围。
-
68-95-99.7 规则: 大约68% 的数据在均值的一个标准差范围内,95% 在两个标准差范围内,99.7% 在三个标准差范围内。
-
均值和方差唯一决定分布: 高斯分布的均值和方差是唯一确定整个分布的两个参数。
1.8 最大似然估计(Maximum Likelihood Estimation)
是一种用于估计模型参数的统计方法。它基于概率论的观点,寻找使观测数据出现的概率最大的参数值。通常记为 L ( θ ∣ d a t a ) L(θ∣data) L(θ∣data),其中 θ 是待估计的参数,为了方便计算,通常取似然函数的对数,得到对数似然函数(Log-Likelihood),记为 ℓ ( θ ∣ data ) \ell(\theta | \text{data}) ℓ(θ∣data)
公式:
Likelihood Function: L ( θ ∣ data ) = ∏ i = 1 n P ( X i ; θ ) \text{Likelihood Function: } L(\theta | \text{data}) = \prod_{i=1}^{n} P(X_i; \theta) Likelihood Function: L(θ∣data)=∏i=1nP(Xi;θ)
Log-Likelihood Function: ℓ ( θ ∣ data ) = ∑ i = 1 n log P ( X i ; θ ) \text{Log-Likelihood Function: } \ell(\theta | \text{data}) = \sum_{i=1}^{n} \log P(X_i; \theta) Log-Likelihood Function: ℓ(θ∣data)=∑i=1nlogP(Xi;θ)
其中, X i X_i Xi 表示每个观测数据点。
1.7 最小二乘法(Least Squares Method)
是一种用于拟合数据和估计模型参数的优化方法。其核心思想是通过最小化观测数据的残差平方和来找到最优的模型参数。这种方法常用于线性回归和其他模型拟合问题
J ( θ ) = 1 2 ∑ i = 1 n ( h θ ( x i ) − y i ) 2 J(\theta) = \frac{1}{2} \sum_{i=1}^{n} (h_\theta(x_i) - y_i)^2 J(θ)=21∑i=1n(hθ(xi)−yi)2
其中, h θ ( x i ) h_\theta(x_i) hθ(xi) 是模型对样本 x i x_i xi 的预测 y ^ \hat y y^, y i y_i yi 是实际观测值。
1.8正规方程 (Normal Equations)
正规方程是用于求解线性回归模型参数的一种解析方法(解方程的一种方法)
θ = ( X T X ) − 1 X T y \theta = (X^T X)^{-1} X^T y θ=(XTX)−1XTy
其中, ( X T X ) − 1 (X^T X)^{-1} (XTX)−1 是矩阵 X T X X^T X XTX 的逆矩阵, X T X^T XT是 X X X的转置矩阵, y y y 是实际观测值。
1.9均方误差(Mean Squared Error, MSE)
MSE是一个用于衡量模型预测与实际观测值之间的差异的指标。对于线性回归模型,MSE定义如下:
MSE = 1 n ∑ i = 1 n ( h θ ( x i ) − y i ) 2 \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (h_\theta(x_i) - y_i)^2 MSE=n1∑i=1n(hθ(xi)−yi)2
其中, h θ ( x i ) h_\theta(x_i) hθ(xi) 是模型对第 i 个样本的预测值, y i y_i yi是实际观测值,n 是样本数量。MSE计算的是平方误差的平均值,其值越小,表示模型对数据的拟合程度越好。
总结:
均方误差 (MSE):
- 用于度量模型预测值与实际观测值之间的平方差的平均值。
- 是一种评估模型性能的指标,越小越好。
最小二乘法 (Least Squares Method):
- 是一种用于估计线性回归模型参数的方法。
- 通过最小化均方误差或其他损失函数来找到最优参数。
- 目标是找到参数,使得模型对观测值的预测误差最小。
通俗理解:
MSE是评估模型好不好,预测准不准用的。最小二乘法是求解方程参数 w 1 , w 2 . . . w_1,w_2... w1,w2...用的
彻底学会系列:一、机器学习之线性回归(二)
相关文章:

彻底学会系列:一、机器学习之线性回归(一)
1.基本概念(basic concept) 线性回归: 有监督学习的一种算法。主要关注多个因变量和一个目标变量之间的关系。 因变量: 影响目标变量的因素: X 1 , X 2 . . . X_1, X_2... X1,X2... ,连续值或离散值。 目标变量: …...

FPGA:我的零基础学习路线(2022秋招已上岸)持续更新中~
可内推简历,丝我即可 前言 初次接触FPGA是在2022年3月左右,正处在研二下学期,面临着暑假找工作,周围的同学大多选择了互联网,出于对互联网的裁员形势下,我选择了FPGA,对于硬件基础知识我几乎是…...

阿里云游戏服务器多少钱一个月?
阿里云游戏服务器租用价格表:4核16G服务器26元1个月、146元半年,游戏专业服务器8核32G配置90元一个月、271元3个月,阿里云服务器网aliyunfuwuqi.com分享阿里云游戏专用服务器详细配置和精准报价: 阿里云游戏服务器租用价格表 阿…...
Win32 SDK Gui编程系列之--ListView自绘OwnerDraw(续)
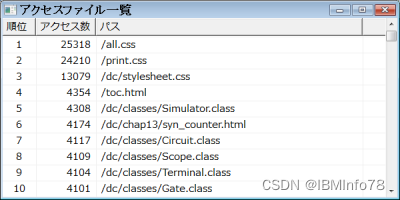
通过所有者绘制的列表视图(2) 所有者绘制列表视图的基础已在前一页中说明。本页将展示如何在所有者绘制列表视图中显示数据库表数据。 1、访问日志 正如在另一个页面中所述,本网站的访问日志目前是通过SQLite3数据库管理的。 以下是上述程序执行的结果。为…...

Android 应用添加系统签名权限的几种方式实现介绍
Android 应用添加系统签名权限的几种方式实现介绍 文章目录 Android 应用添加系统签名权限的几种方式实现介绍一、前言二、Android 应用添加系统签名权限的几种方式介绍1、在Android Studio添加系统签名文件2、源码编译apk添加系统签名Android.mkAndroid.bp 3、源码编译app代码…...

麒麟V10+飞腾处理器源码编译qt
1.下载qt源码 2.百度解压命令,进行解压 3.cd进文件目录 4.使用./configure命令进行配置(重点:记得看说明) Usage: configure [-h] [-prefix <dir>] [-prefix-install] [-bindir <dir>] [-libdir <dir>][-docdir <dir>] [-headerdir <dir&g…...
MacOS 查AirPods 电量技巧:可实现低电量提醒、自动弹窗
要怎么透过macOS 来查询AirPods 电量呢?当AirPods 和Mac 配对后,有的朋友想通过Mac来查询AirPods有多少电量,这个里有几个技巧,下面我们来介绍一下。 透过Mac 查AirPods 电量技巧 技巧1. 利用状态列上音量功能查询 如要使用此功能…...
python介绍,安装Cpython解释器,IDE工具pycharm的使用
python介绍 官方的Python解释器本质是基于C语言开发的一个软件,该软件的功能就是读取以py.结尾的文件内容,然后按照Guido定义好的语法和规则去翻译并执行相应的代码。这种C实现的解释器被称为Cpython。 python解释器的种类:Jython IPyth…...
服务器安装Docker (centOS)
1. 卸载旧版本的Docker(如果有) 首先,如果您的系统上安装了旧版本的Docker,需要将其卸载。Docker的旧版本称为docker或docker-engine。使用以下命令来卸载旧版本: sudo yum remove docker \ docker-client \ docker-…...

解析spritf和sscanf与模拟常用字符串函数strchr,strtok(二)
今天又来继续我们的字符串函数的文章,这也是最后一篇了。希望这两篇文章能让各位理解透字符串函数。 目录 strchr strtok sprintf和sscanf strchr strchr 是一个用于在字符串中查找特定字符首次出现位置的函数。以下是解析和模拟实现 strchr 函数的示例&…...
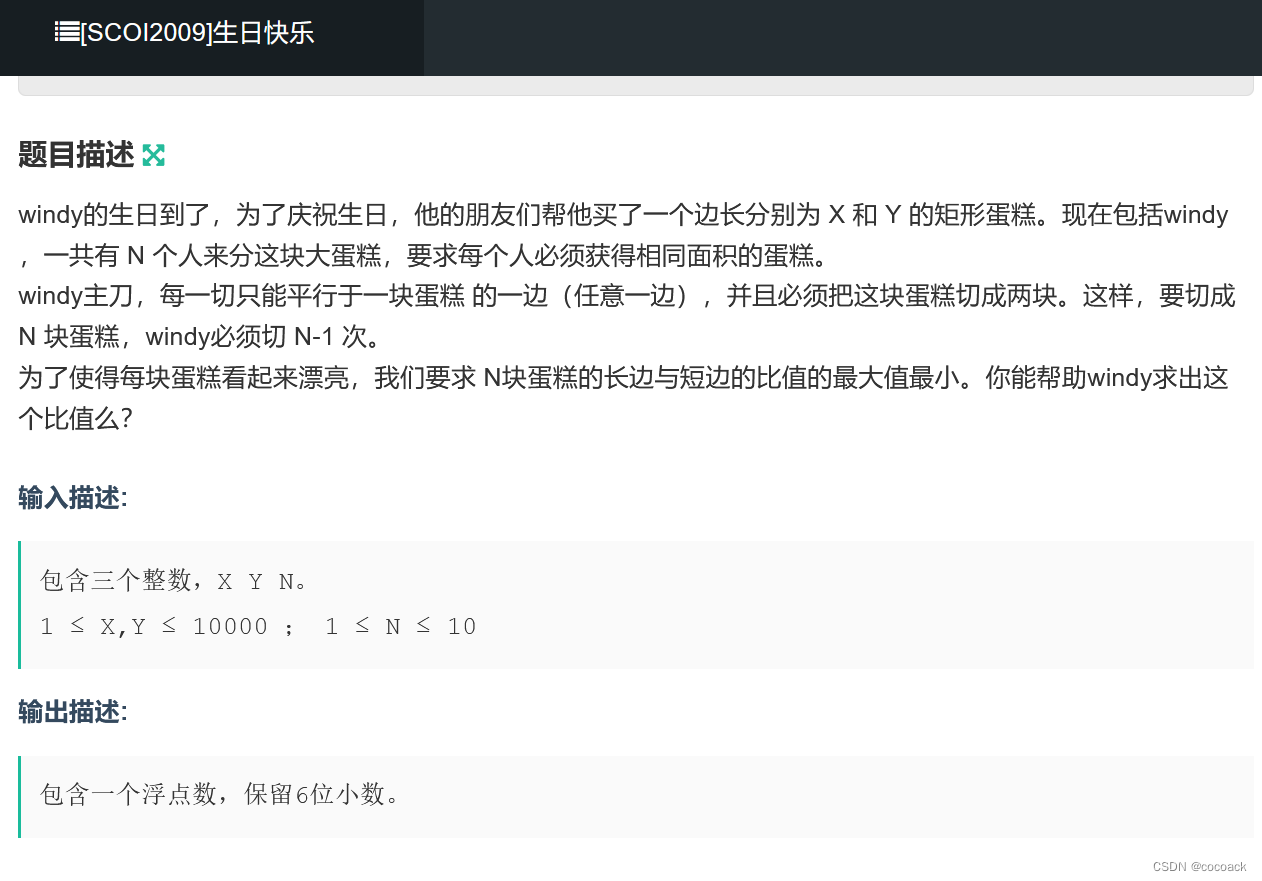
备战蓝桥杯---搜索(进阶4)
话不多说,直接看题: 下面是分析: (ab)%c(a%cb%c)%c; (a*b)%c(a%c*b%c)%c; 因此,如果两个长度不一样的值%m为相同值,那就舍弃长的(因为再加1位只不过是原来值*10那位值,因此他们得出的%m还是同…...
:定时器时钟)
51单片机基础(C语言):定时器时钟
1.使用定时器 1 和LCD1602设计一个简易数字时钟。 main.c #include <REGX52.H> #include "Delay.h" #include "LCD1602.h" #include "Timer0.h"unsigned char Sec55,Min59,Hour23;void main() {LCD_Init();Timer0Init();LCD_ShowString(…...

单片机无线发射的原理剖析
目录 一、EV1527编码格式 二、OOK&ASK的简单了解 三、433MHZ 四、单片机的地址ID 五、基于STC15W104单片机实现无线通信 无线发射主要运用到了三个知识点:EV1527格式;OOk;433MHZ。下面我们来分别阐述: EV1527是数据的编…...

Redis的过期键的删除策略
我们都知道,Redis是key-value数据库,我们可以设置Redis中缓存的key的过期时间。Redis的过期策略就是指当Redis中缓存的key过期了,Redis如何处理。 过期策略通常有以下三种: 定时过期:每个设置过期时间的key都需要创建…...

放假--寒假自学版 day1(补2.5)
fread 函数: 今日练习 C语言面试题5道~ 1. static 有什么用途?(请至少说明两种) 1) 限制变量的作用域 2) 设置变量的存储域 2. 引用与指针有什么区别? 1) 引用必须被初始化,指针不必。 2) 引用初始…...
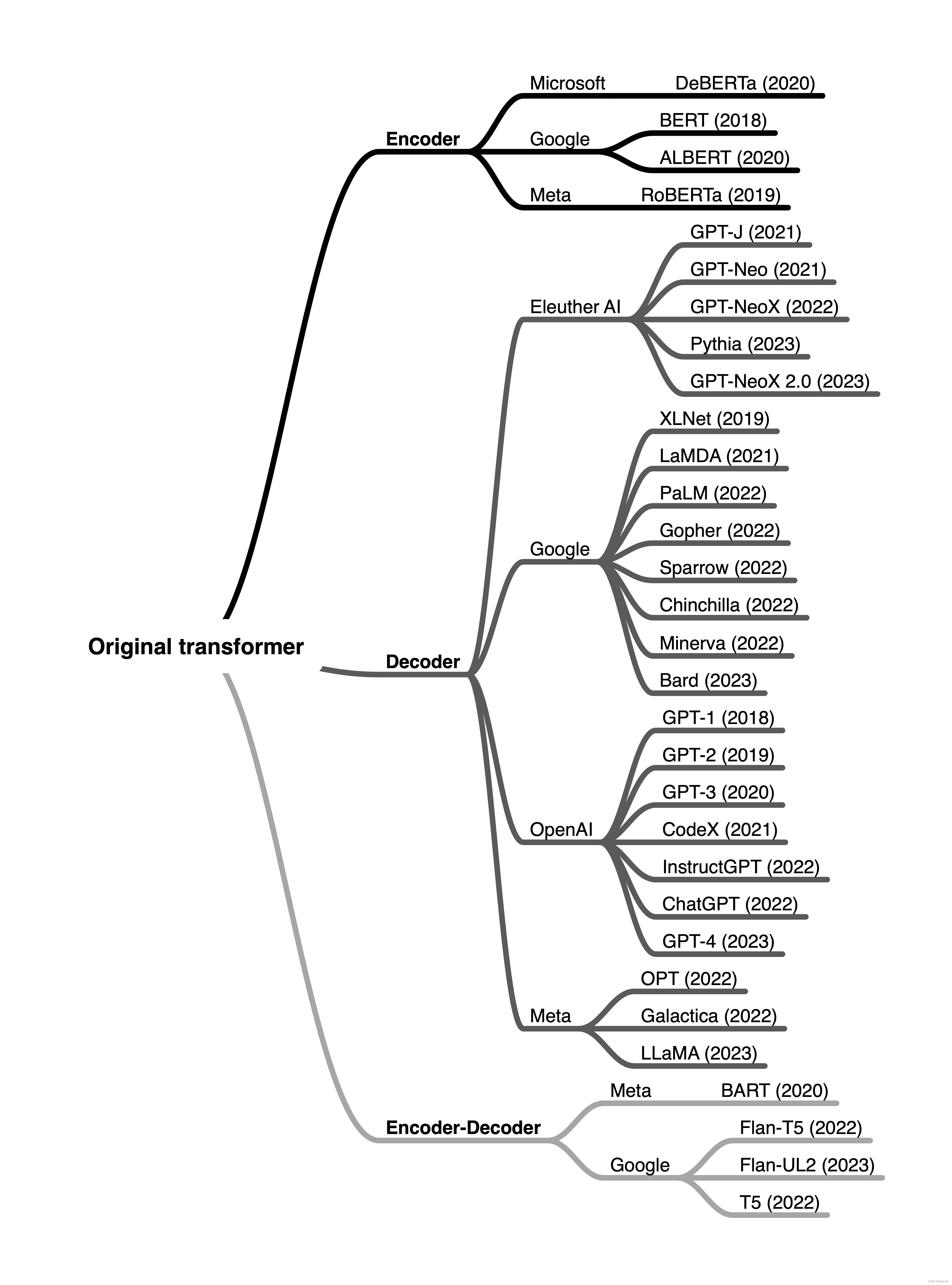
LLM(5) | Encoder 和 Decoder 架构
LLM(5) | Encoder 和 Decoder 架构 文章目录 LLM(5) | Encoder 和 Decoder 架构0. 目的1. 概要2. encoder 和 decoder 风格的 transformer (Encoder- And Decoder-Style Transformers)原始的 transformer (The original transformer)编码器 (Encoders)解码器 (Decoders)编码器和…...
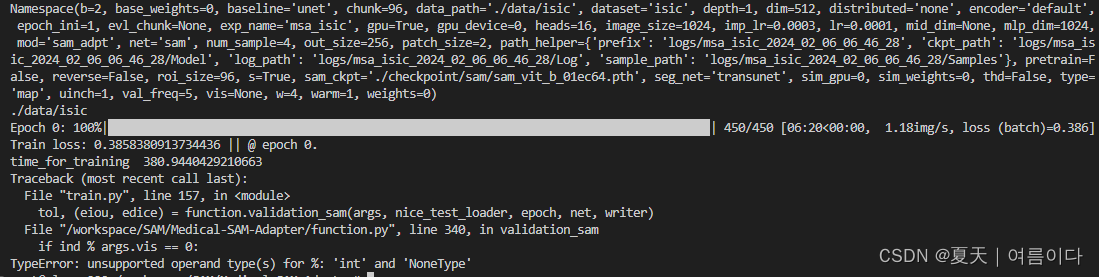
CV | Medical-SAM-Adapter论文详解及项目实现
******************************* 👩⚕️ 医学影像相关直达👨⚕️******************************* CV | SAM在医学影像上的模型调研【20240207更新版】-CSDN博客 CV | Segment Anything论文详解及代码实现 本文主要讲解Medical-SAM-Adapter论文及项…...
C++初阶:容器(Containers)vector常用接口详解
介绍完了string类的相关内容后:C初阶:适合新手的手撕string类(模拟实现string类) 接下来进入新的篇章,容器vector介绍: 文章目录 1.vector的初步介绍2.vector的定义(constructor)3.v…...

flink写入es的参数解析
ElasticsearchSink内部使用BulkProcessor一次将一批动作(ActionRequest)发送到ES集群。在发送批量动作前,BulkProcessor先缓存,再刷新。缓存刷新的间隔,支持基于Action数量、基于Action大小、基于时间间隔3种策略。BulkProcessor支持在同一次…...

逆向工程:揭开科技神秘面纱的艺术
在当今这个科技飞速发展的时代,我们每天都在与各种电子产品、软件应用打交道。然而,你是否想过,这些看似复杂的高科技产品是如何被创造出来的?今天,我们就来探讨一下逆向工程这一神秘而又令人着迷的领域。 一、什么是…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
