爪哇部落算法组2024新生赛热身赛题解
第一题(签到):
1、题意:
2、题解:
我们观察到happynewyear的长度是12个字符,我们直接从前往后遍历0到n - 12的位置(这里索引从0开始),使用C++的substr()函数找到以i开头的长度为12的字符串是不是我们要的,如果是的话直接输出,注意输出时索引是从0开始。
3、代码:
#include <bits/stdc++.h> using namespace std; const int N = 1e5 + 10; int n; int main() {string s; cin >> n >> s; for(int i = 0; i < n - 12; i ++ ) {string tmp = s.substr(i, 12); if(tmp == "happynewyear") {cout << i << endl; return 0; }}return 0; }
第二题(思维构造):
1、题意:
2、题解:对于任意数字%7的解集是
, ,操作2我们可以构造方案为
使得得到了7的倍数,当任意要构造0-6时,我们发现会多出几个空位出来,当余数为x时我们构造7-x, 显然 0 <= 7 - x <= 7,当我们先给7-x分配好了二进制位置,可以发现0-6都只占二进制位1个,2个,会剩下5个或者4个,我们只需要多次执行操作二凑出7的二进制的占位的个数的倍数(只需要按构造方案那样的思想造不同的二进制位),就一定能构造出任意情况。
3、代码#include <bits/stdc++.h> using namespace std; using ll = long long; ll n, m; ll a[N], s[N]; int main() {int T; cin >> T; while(T -- ) {string s; cin >> s; cout << "YES" << endl; }return 0; }
第三题(前缀和):
1、题意:
2、题解:
维护好长度为n的前缀和,每次到达<= n - m + 1的位置我们直接对取Max即可
3、代码:#include <bits/stdc++.h> using namespace std; using ll = long long; const int N = 2e5 + 10; ll n, m; ll a[N], s[N]; int main() {cin >> n >> m; ll ans = -1; for(int i = 1; i <= n; i ++ ) {cin >> a[i];s[i] = a[i] + s[i - 1]; }for(int i = 1; i <= n - m + 1; i ++ )ans = max(ans, s[i + m - 1] - s[i - 1]); cout<<ans<<endl; return 0; }
第四题 (贪心 + 维护):
1、题意:
2、题解:
我们先维护好"AB"的每个位置和"BA"的每个位置,都是第一个字符出现的位置,遍历"AB"位置,二分出左边离它最远的"BA"位置,判断一下这个位置是否是和它差>=3的长度,如果是就是合法的,再二分出右边离它最远的"BA"位置,判断一下这个位置是否和它差>=3长度, 如果是就说合法的。
3、代码:
#include <bits/stdc++.h> using namespace std; const int N = 2e5 + 10; int n, m; void solve() {string s;cin >> s; n = s.size();vector<int> ab, ba; for(int i = 0; i < n - 1; i ++ ) {string tmp; tmp += s[i]; tmp += s[i + 1]; if(tmp == "AB") ab.push_back(i);if(tmp == "BA") ba.push_back(i);}bool flag = 0; for(int i = 0; i < ab.size(); i ++ ) {int x = ab[i], i1 = -1, i2 = -1; int l = 0, r = ba.size() - 1; while(l < r) {int mid = l + r >> 1; if(ba[mid] < x - 1) r = mid; else l = mid + 1; }i1 = l;l = 0, r = ba.size() - 1; while(l < r) {int mid = l + r + 1 >> 1; if(ba[mid] > x + 1) l = mid; else r = mid - 1; }i2 = l;if(ba.size() && ba[i1] < x - 1) {flag = 1; break; }if(ba.size() && ba[i2] > x + 1) {flag = 1;break; }}if(flag) puts("YES");else puts("NO"); } int main() {int ts = 1;cin >> ts;while(ts --) solve();return 0; }
相关文章:

爪哇部落算法组2024新生赛热身赛题解
第一题(签到): 1、题意: 2、题解: 我们观察到happynewyear的长度是12个字符,我们直接从前往后遍历0到n - 12的位置(这里索引从0开始),使用C的substr()函数找到以i开头的长度为12的字…...
)
1123. 铲雪车(欧拉回路)
活动 - AcWing 随着白天越来越短夜晚越来越长,我们不得不考虑铲雪问题了。 整个城市所有的道路都是双向车道,道路的两个方向均需要铲雪。因为城市预算的削减,整个城市只有 1 辆铲雪车。 铲雪车只能把它开过的地方(车道)的雪铲干…...
网络协议与攻击模拟_15FTP协议
了解FTP协议 在Windows操作系统上使用serv-U软件搭建FTP服务 分析FTP流量 一、FTP协议 1、FTP概念 FTP(文件传输协议)由两部分组成:客户端/服务端(C/S架构) 应用场景:企业内部存放公司文件、开发网站时利…...

「效果图渲染」效果图与3D影视动画渲染平台
效果图渲染和3D影视动画渲染都是视觉图像渲染的领域应用。效果图渲染主要服务于建筑、室内设计和产品设计等行业,这些领域通常对视觉呈现的精度和细节有较高要求。与之相比,3D影视动画渲染则普遍应用于电影、电视、视频游戏和广告等媒体领域,…...

Blender_查看版本
Blender_查看版本 烦人的烦恼,没找见哪儿可以查看版本? 算是个隐蔽的角落!...

node.js 读目录.txt文件,用 xml2js 转换为json数据,生成jstree所需的文件
请参阅:java : pdfbox 读取 PDF文件内书签 请注意:书的目录.txt 编码:UTF-8,推荐用 Notepad 转换编码。 npm install elementtree ; npm install xml2js ; node.js 用 elementtree读目录.txt文件,用 xml2js 转换为…...

【Docker】02 镜像管理
文章目录 一、Images镜像二、管理操作2.1 搜索镜像2.1.1 命令行搜索2.1.2 页面搜索2.1.3 搜索条件 2.2 下载镜像2.3 查看本地镜像2.3.1 docker images2.3.2 --help2.3.3 repository name2.3.4 --filter2.3.5 -q2.3.6 --format 2.4 给镜像打标签2.5 推送镜像2.6 删除镜像2.7 导出…...

了解海外云手机的多种功能
随着社会的高度发展,海外云手机成为商家不可或缺的工具,为企业出海提供了便利的解决方案。然而,谈及海外云手机,很多人仍不了解其强大功能。究竟海外云手机有哪些功能,可以为我们做些什么呢? 由于国内电商竞…...

白酒:自动化生产线的优势与实践
随着科技的进步,自动化生产线在各行各业的应用越来越广泛。云仓酒庄的豪迈白酒在生产过程中,也积极引入自动化生产线,以提升生产效率、品质和安全性。 首先,自动化生产线能够显著提高生产效率。传统的手工生产线在生产过程中容易受…...
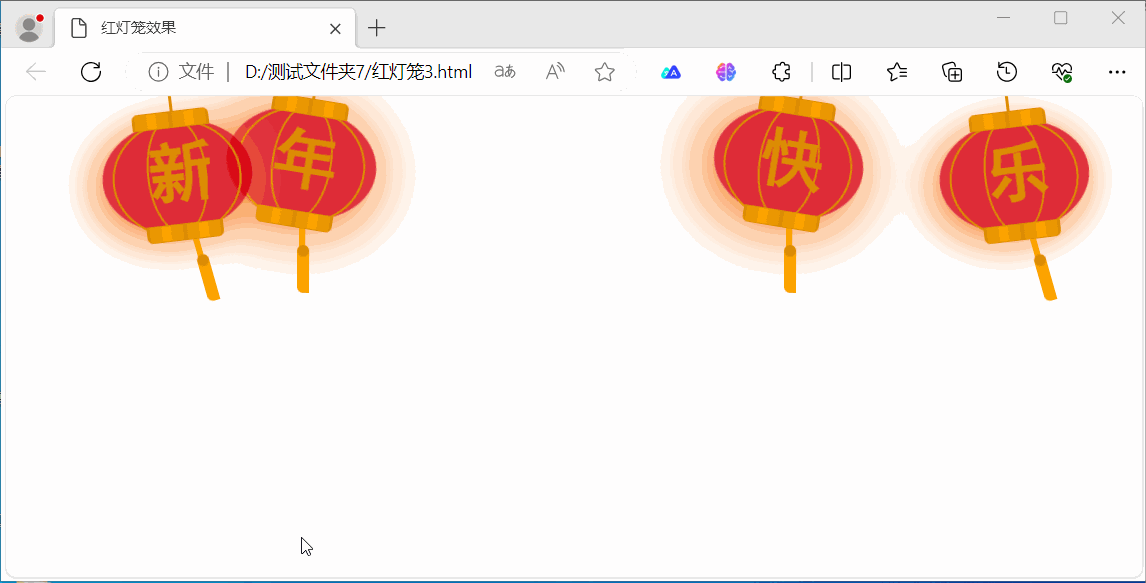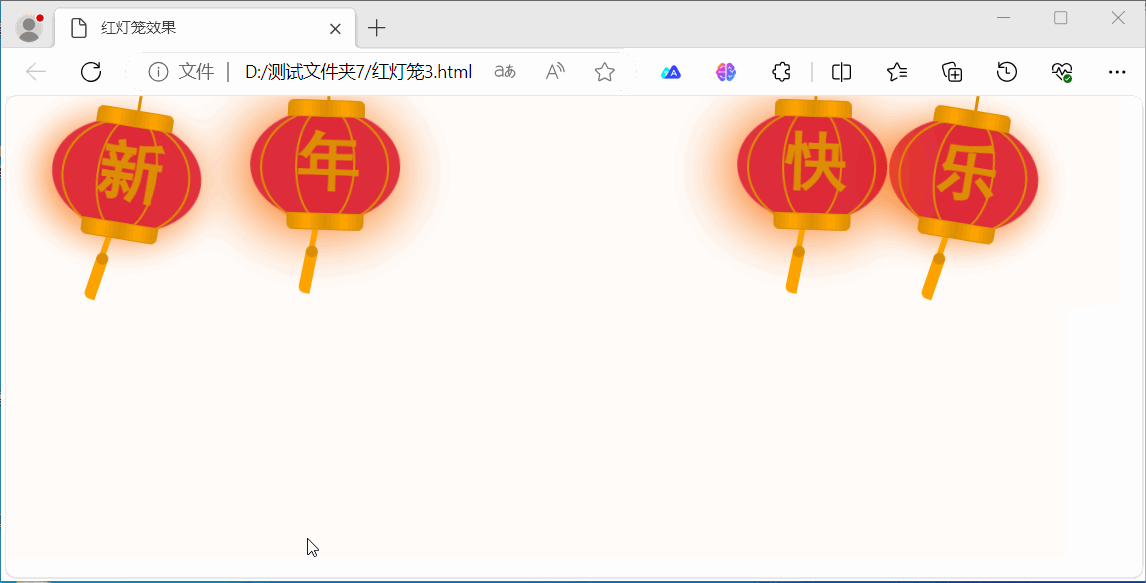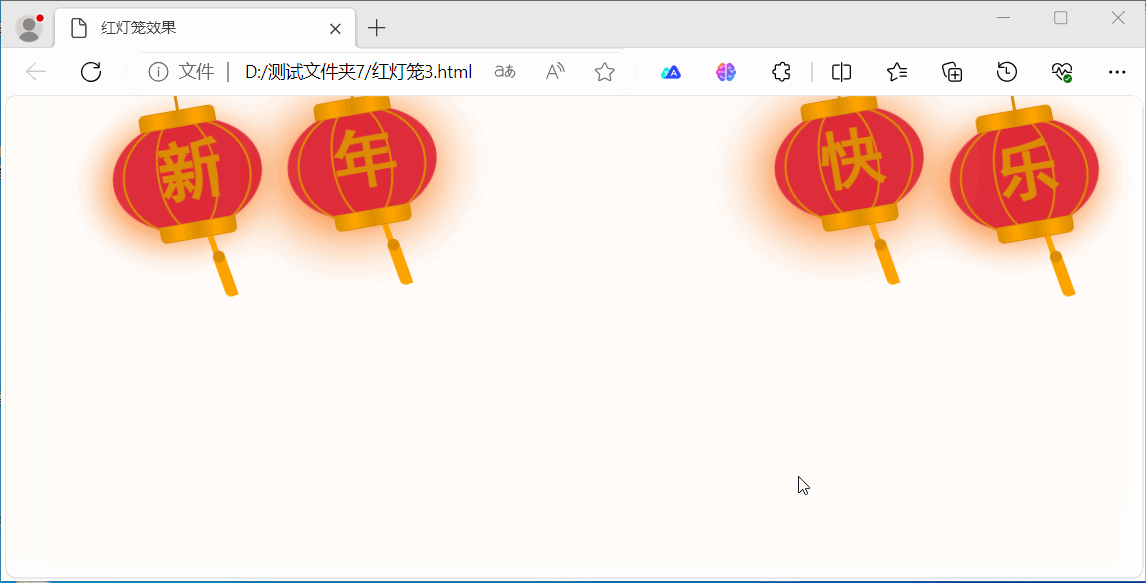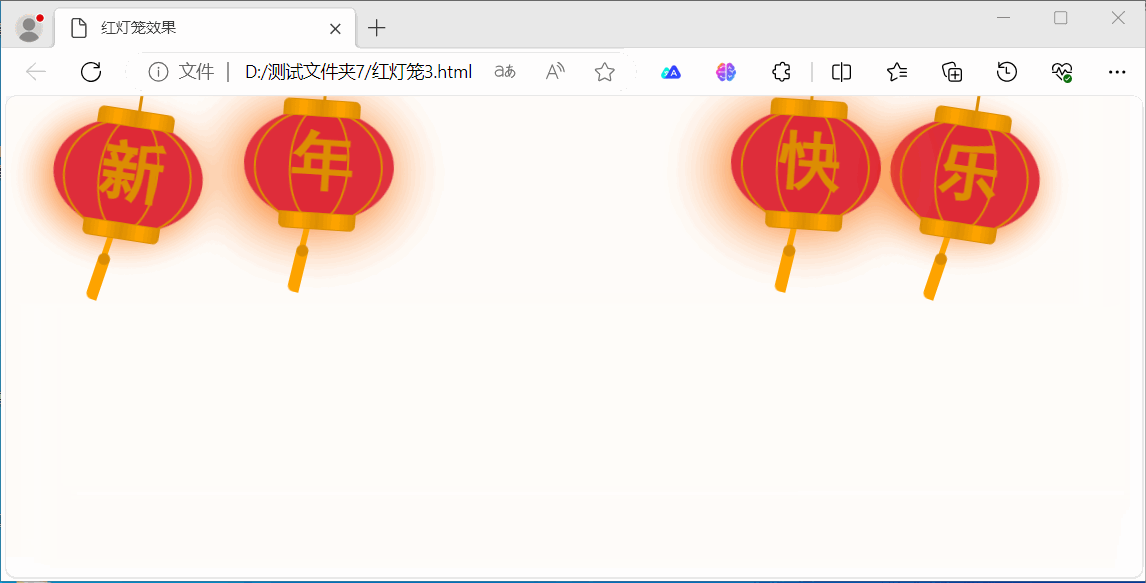
用HTML5实现灯笼效果
本文介绍了两种实现效果:一种使用画布(canvas)标签/元素,另一种不用画布(canvas)标签/元素主要使用CSS实现。 使用画布(canvas)标签/元素实现,下面,在画布上…...
事务XID分配与主备XID同步)
Postgresql源码(120)事务XID分配与主备XID同步
参考 《Postgresql源码(25)子事务可见性判断和性能问题》 XID获取顶层入口 函数:AssignTransactionId static void AssignTransactionId(TransactionState s) {...优先给没有事务ID的父事务分配 确保父事务有 XID,以便子事务总是…...
)
B2077 角谷猜想(洛谷)
题目描述 所谓角谷猜想,是指对于任意一个正整数,如果是奇数,则乘 33 加 11,如果是偶数,则除以 22,得到的结果再按照上述规则重复处理,最终总能够得到 11。如,假定初始整数为 55&…...

排序算法---归并排序
原创不易,转载请注明出处。欢迎点赞收藏~ 归并排序是一种常见的排序算法,它采用了分治的思想。它将一个待排序的数组递归地分成两个子数组,分别对两个子数组进行排序,然后将排好序的子数组合并成一个有序数组。 具体的归并排序过…...

[WUSTCTF2020]朴实无华(特详解)
一开始说header出问题了 就先dirsaerch扫一遍 发现robot.txt 访问一下 去看看,好好好,肯定不是得 他一开始说header有问题,不妨抓包看看,果然有东西 访问看看,乱码修复一下,在之前的博客到过 <img src…...
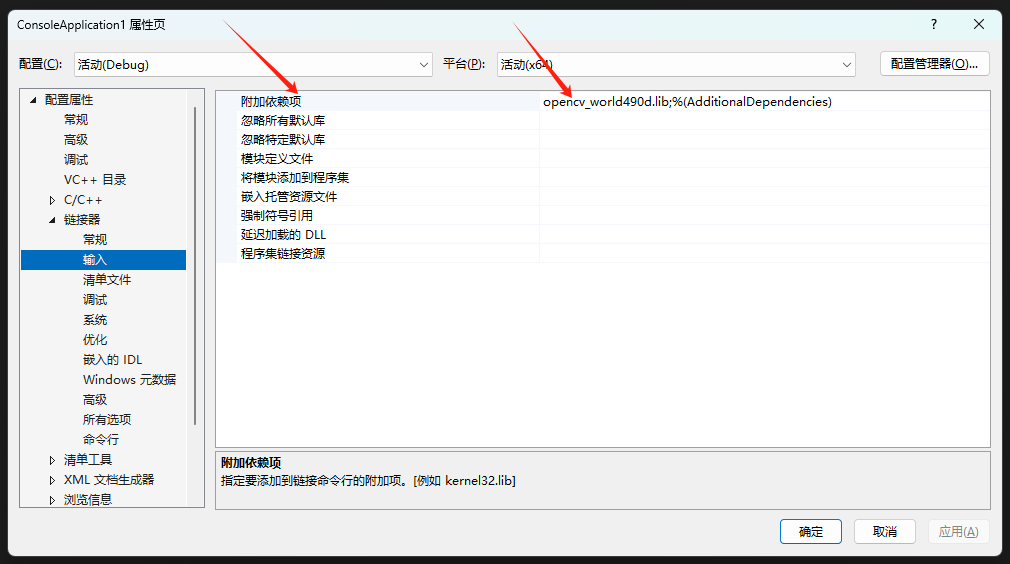
下载已编译的 OpenCV 包在 Visual Studio 下实现快速配置
自己编译 OpenCV 挺麻烦的,配置需要耗费很长时间,编译也需要很长时间,而且无法保证能全部编译通过。利用 OpenCV 官网提供的已编译的 OpenCV 库可以节省很多时间。下面介绍安装配置方法。 1. OpenCV 官网 地址是:https://opencv…...

【Linux系统学习】3.Linux用户和权限
Linux用户和权限 1.认知root用户 1.1 root用户(超级管理员) 无论是Windows、MacOS、Linux均采用多用户的管理模式进行权限管理。 在Linux系统中,拥有最大权限的账户名为:root(超级管理员) 而在前期&#…...

视频美颜SDK开发指南:从入门到精通的技术实践
美颜SDK是一种强大的工具,它不仅仅可以让用户在实时视频中获得光滑的肌肤和自然的妆容,从简单的滤镜到复杂的人脸识别,美颜SDK涵盖了广泛的技术领域。 一、美颜SDK的基本原理 美颜SDK包括图像处理、人脸检测和识别、滤镜应用等方面。掌握这些…...

Electron基本介绍
Electron基本介绍 Electron 官方网站:https://www.electronjs.org/zh/ Electron安装方法:npm install electron -g 全局安装 Electron简介:Electron提供了丰富的本地(操作系统)API,使你能够使用纯JavaScr…...

使用网关过滤器,根据业务规则实现微服务动态路由
文章目录 业务场景拦截器实现Spring Cloud Gateway介绍 业务场景 我们服务使用Spring Cloud微服务架构,使用Spring Cloud Gateway 作为网关,使用 Spring Cloud OpenFeign 作为服务间通信方式作为网关,主要作用是鉴权与路由转发。大多数应用场…...

PKI - 03 密钥管理(如何进行安全的公钥交换)
文章目录 Pre密钥管理面临的挑战安全密钥管理的几种方式手动密钥交换与确认受信任的介绍 Pre PKI - 02 对称与非对称密钥算法 密钥管理面临的挑战 密钥管理面临的挑战主要包括以下几点: 安全的公钥交换:在使用基于非对称密钥算法的服务之前,…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...



