关于一笔画问题的一些思考(欧拉路Fleury算法、逐步插入回路法、以及另一种可能的解法)
前言
这是一个经典的图论问题了
最近复习离散的时候又恰好看到了,发现自己以前的解法似乎有点bug
然后开始出反例卡自己,结果发现卡不掉?
然后再好好想了想,发现这个看起来有问题的做法可能确实没问题。
注意:欧拉路、欧拉回路、欧拉图、半欧拉图四个概念的区别
Fleury算法
这是离散数学书上的经典求解欧拉路的算法之一

非常好理解,只不过如何快速判断正在删边的图的桥实现起来比较麻烦,如果没有好的数据结构的支持,时间复杂度将会多乘一个(n+m),所以正常情况下我们不用Fleury算法来求解欧拉路
逐步插入回路法
这个方法离散数学书上并没有细讲,而仅仅只用一句话带过了

我们可以先来看看定理15.1(欧拉回路的判定定理)的充分性证明
充分性:G是无向连通图且没有奇度顶点=>G中存在欧拉回路(G是欧拉图)


大致意思就是
(1)G中必定存在圈
书中用可以证明四个字带过了
这个可以用极大路径法证明
因为δ(G)≥2,那么找一条图中的极大路径,路径的端点一定存在一条边连向路径中的点(否则路径就可以继续延长,与极大路径矛盾),这样就会构成一个圈。
(2)删掉这个圈后,剩下的连通分支都是欧拉图(由归纳法假设可得)
(3)以这个大圈上的一点为出发点,走到与删掉后的连通分支上的点后,先把子欧拉回路走完,然后再继续向前走。
证明过程如此,那么如何将其转换为算法呢?
可以利用归纳法的思想,对图G进行分治,先任意找圈,然后删圈,判连通性,在各个连通分支递归,答案返回后再一起整合……反正写起来巨麻烦,而且没必要
另一种可能的解法
为什么说是可能呢,因为我也感觉自己不能很严谨的证明这个做法的正确性
先上代码:

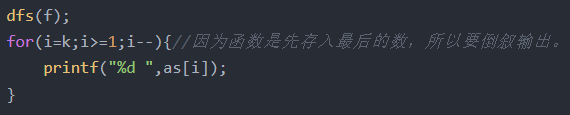
这里省略了对图进行(半)欧拉图判定的过程以及选起始点的过程
只保留了计算的主体部分
可以说是非常诡异,初看时觉得有点道理,细想之后发现完全不对劲,但是它却AC了
于是我开始举反例
8
0 1 1 1 1 0 1 1
1 0 1 0 0 0 0 0
1 1 0 0 0 0 0 0
1 0 0 0 1 1 0 0
1 0 0 1 0 1 0 0
0 0 0 1 1 0 0 0
1 0 0 0 0 0 0 1
1 0 0 0 0 0 1 0
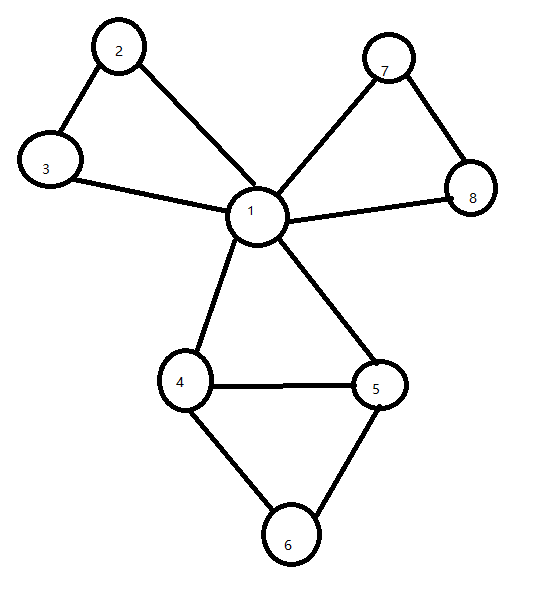

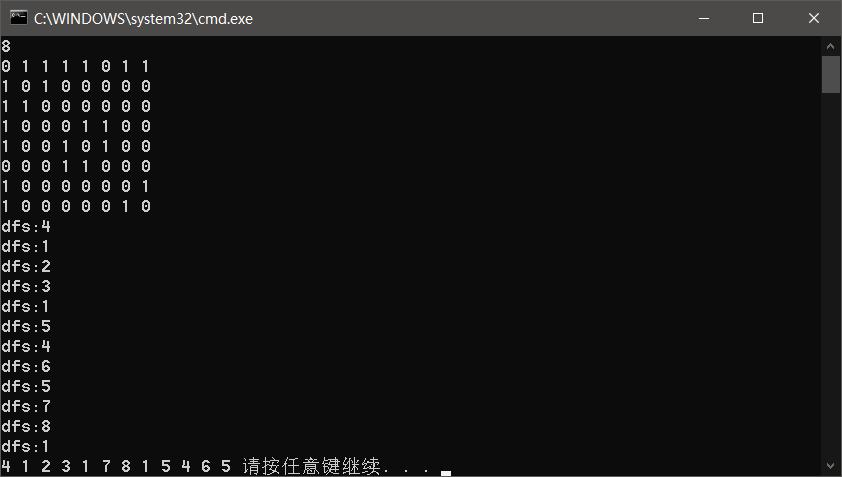
可以发现程序的dfs过程确实时错误的,但是最后输出的结果确实对的
关键就是在于保存答案的位置和输出答案的顺序。
dfs输出的位置是入栈的位置,而保存答案的位置是出栈的位置
Fluery算法告诉我们,我们在做一笔画时出错的原因是,在不必要的时候先走了桥,导致没办法走回来
也就是说,我们应该最后走桥
虽然这个做法中我们并不能保证我们最后走的是桥
但是我们知道
先走桥的肯定会先出栈(因为会走不通,导致退栈回溯)
所以过桥的答案一定会被先统计到
而且最后又是倒序输出,这样就间接地保证了过桥之后的答案最后输出
也就间接地保证了这个做法的正确性。
这个做法是OI中比较普遍的欧拉路求解算法,然而我的这个证明是很不严谨的,希望有识之士可以补充更加严谨的证明。
完结撒花~~~~( •̀ ω •́ )y
相关文章:

关于一笔画问题的一些思考(欧拉路Fleury算法、逐步插入回路法、以及另一种可能的解法)
前言这是一个经典的图论问题了最近复习离散的时候又恰好看到了,发现自己以前的解法似乎有点bug然后开始出反例卡自己,结果发现卡不掉?然后再好好想了想,发现这个看起来有问题的做法可能确实没问题。注意:欧拉路、欧拉回…...
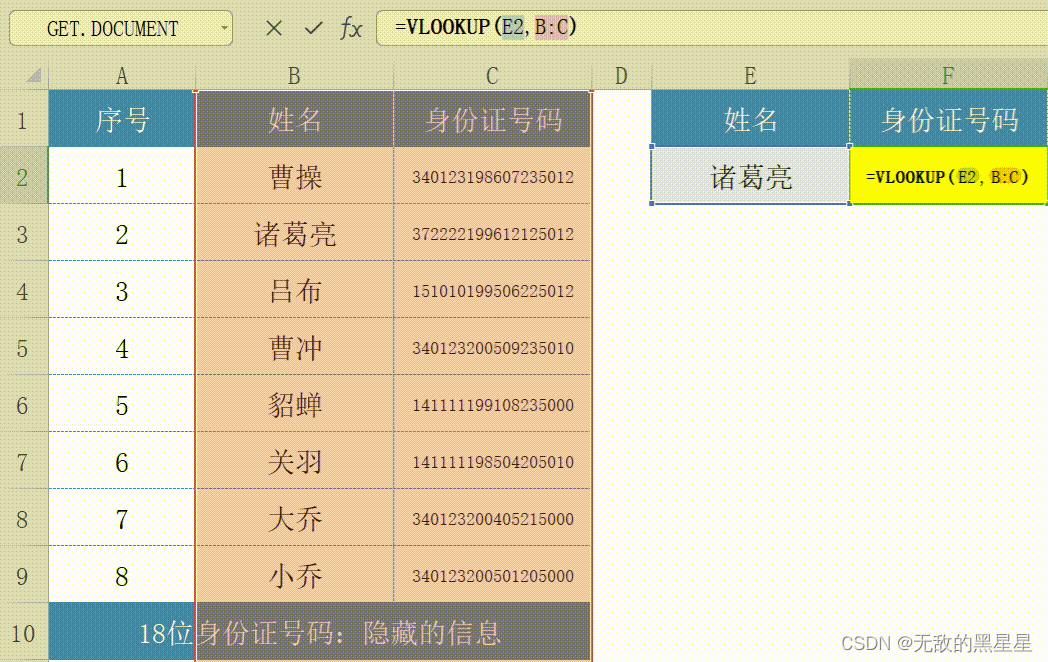
vlookup怎么用详细步骤,看这一篇就够了
1、vlookup函数:使用方法 以下便是vlookup函数,功能、语法和参数用法: excel函数vlookup 2、vlookup函数:查询参数 首先,选中F2单元格,然后在编辑栏输入函数公式:VLOOKUP(E2,B&…...

雅思经验(9)之小作文常用词汇总结
写作:关于趋势的上升和下降在小作文中,真的是非常常见的,所以还是要积累一下。下面给出了很多词,但是在雅思写作中并不是词越丰富,分数就越高的。雅思写作强调的是准确性:在合适的地方用合适的词和句法。不…...

【Python语言基础】——Python NumPy 数组创建
Python语言基础——Python NumPy 数组创建 文章目录 Python语言基础——Python NumPy 数组创建一、Python NumPy 数组创建一、Python NumPy 数组创建 创建 NumPy ndarray 对象 NumPy 用于处理数组。 NumPy 中的数组对象称为 ndarray。 我们可以使用 array() 函数创建一个 NumP…...

【大数据】Hadoop-Kms 安装及相关详细配置,看完你就会了
简介 Hadoop KMS是基于Hadoop的KeyProvider API的加密密钥管理服务器,它提供了使用REST API通过HTTP进行通信的客户端和服务器组件。 客户端是一个KeyProvider实现,使用KMS HTTP REST API与KMS交互。 KMS及其客户端具有内置的安全性,它们支…...

SpringCloud分布式框架
SpringCloud分布式框架 SpringCloud框架 Spring Cloud 是一个用于创建分布式系统的开源框架。它基于 Spring Boot 和 Spring Framework,提供了一整套关于分布式系统的工具和技术。 Spring Cloud 是微服务架构的一种实现方式,它提供了一整套完整的技术…...

Csss属性display,visibility区别,对渲染页面的影响
display: none; 与 visibility: hidden; 的区别 相同: 它们都能让元素不可见 区别:display:none;会让元素完全从渲染树中消失,渲染的时候不占据任何空间; visibility: hidden;不会让元素从渲染树消失,渲染时元素继续…...

怎么给笔记本电脑外接两台显示器?
我们在办公室会看见不少同事的电脑不止一台显示器,多屏确实可以提高工作效率。有的游戏党也会选择给电脑外接显示器,带来绝佳的体验。 不过要怎么把将外部显示器连接到笔记本电脑上?驱动人生在这里教给大家给笔记本外接显示器的做法。 一、…...
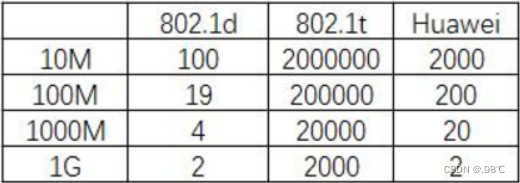
生成树协议 — STP
目录 一、环路的出现 1、广播风暴: 2、MAC地址表翻滚: 二、生成树 1、定义: 2、生成树使用的算法: 三、802.1D 1、BPDU: 2、TCN—拓扑变更消息(也是BPDU): 3、部分名词&am…...
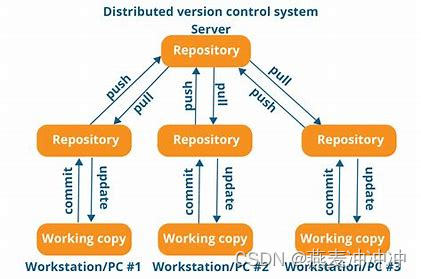
git必会的知识点
注:本文参考https://www.liaoxuefeng.com/wiki/896043488029600 原文非常值得一读,作者学识渊博,补充了很多有意思的知识。我仅仅是拾人牙慧。 git是最先进的分布式版本控制系统。 版本控制系统——自动记录系统中文件的改动情况࿰…...

【hello, world】计算机系统漫游
文章目录hello程序信息就是位 上下文程序被其他程序翻译成不同的格式预处理阶段编译阶段汇编阶段链接阶段了解编译系统如何工作是大有益处的优化程序性能理解链接时出现的错误避免安全漏洞处理器读并解释储存在内存中的指令系统的硬件组成总线I/O设备主存处理器运行hello程序高…...
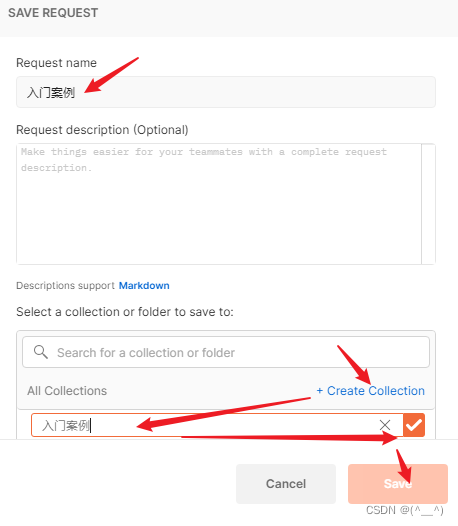
1. SpringMVC 简介
文章目录1. SpringMVC 概述2. SpringMVC 入门案例2.1 入门案例2.2 入门案例工作流程3. bean 加载控制4. PostMan 工具1. SpringMVC 概述 SpringMVC 与 Servlet 功能等同,均属于 Web 层开发技术。SpringMVC 是 Spring 框架的一部分。 对于 SpringMVC,主…...

《解谜三星堆:开启中华文明之门》-范勇 笔记
甲篇 应重视民间流传的疑似三星堆的文物,对其展开充分的研究,以发现更多关于三星堆的秘密,并且避免“敦煌窘境”,让我国的三星堆学术研究处于世界领先地位!(书中就讲到了在民间首次发现了圆形玉器…...
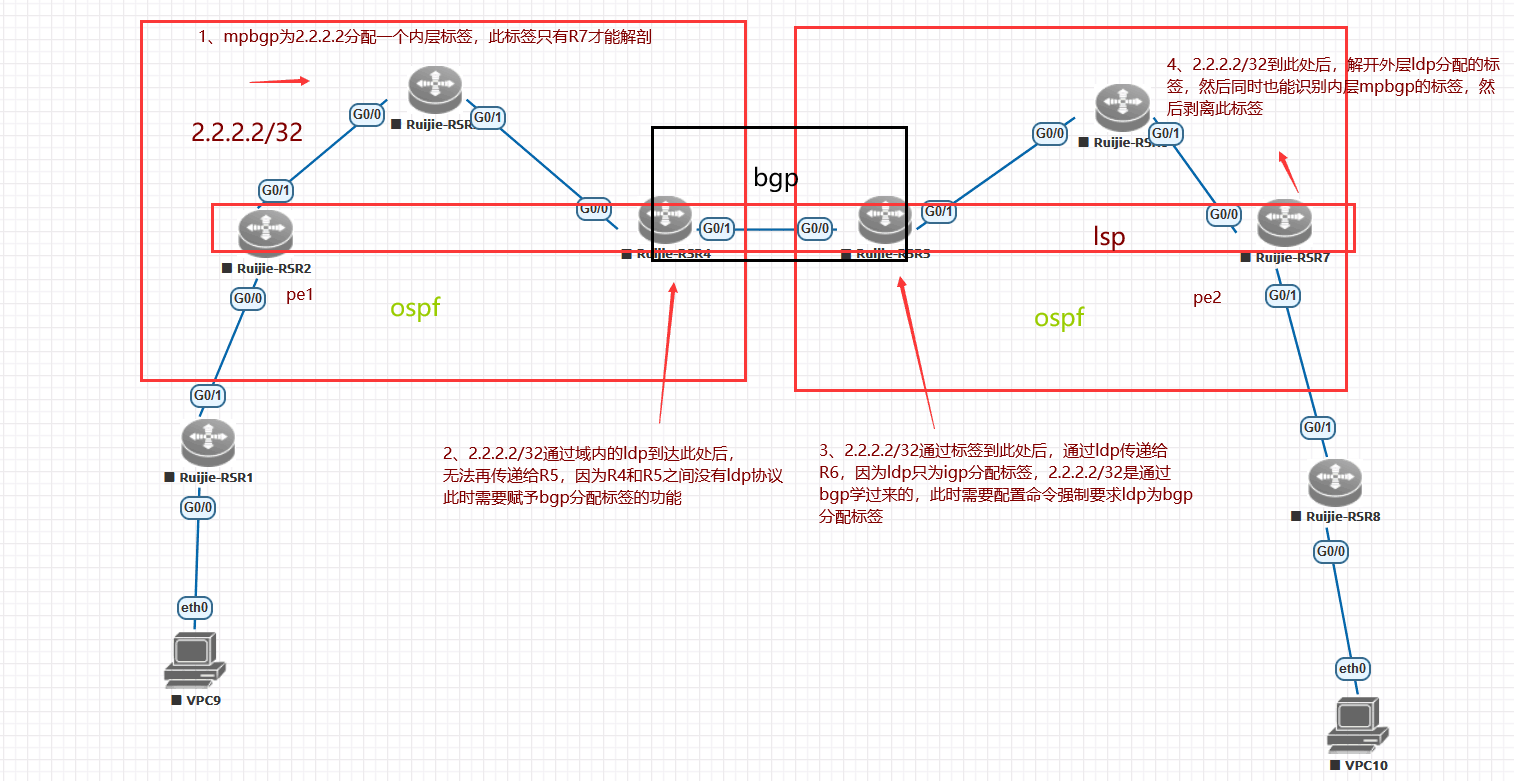
锐捷(十四)mpls vxn optionc的关键问题所在和具体问题分析
用锐捷的设备搭建mpls vxn optionc的基础版和带RR的版本,在控制平面和转发平免上分析mpls vxn optionc的关键问题所在和具体问题分析。一 基础mpls vxn optionc:核心:两pe之间之间建立MP EBGP邻居,从而直接传递路由解放了ASBR。关…...

Python语言零基础入门教程(十四)
Python 日期和时间 Python 程序能用很多方式处理日期和时间,转换日期格式是一个常见的功能。 Python 提供了一个 time 和 calendar 模块可以用于格式化日期和时间。 时间间隔是以秒为单位的浮点小数。 每个时间戳都以自从1970年1月1日午夜(历元&…...
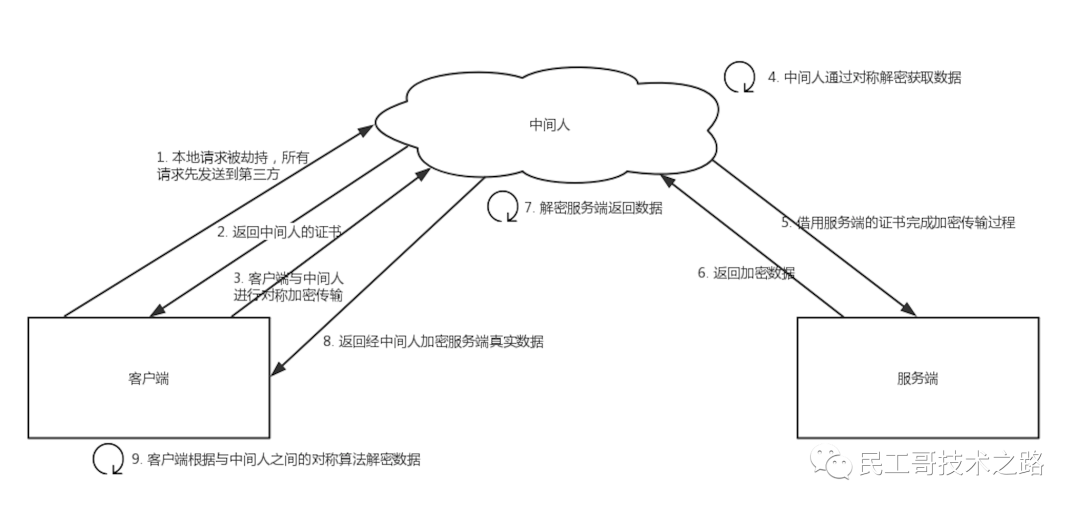
Https 协议超强讲解(一)
都说Https协议非常安全,那为什么还是会被抓包呢?抓包后会影响什么吗? HTTPS协议 随着 HTTPS 建站的成本下降,现在大部分的网站都已经开始用上 HTTPS 协议。大家都知道 HTTPS 比 HTTP 安全,也听说过与 HTTPS 协议相关…...

5.Redis 实现点赞 优化登陆(验证码 token..)
Redis(1)简介Redis 是一个高性能的 key-value 数据库原子 – Redis的所有操作都是原子性的。多个操作也支持事务,即原子性,通过MULTI和EXEC指令包起来。非关系形数据库数据全部存在内存中,性能高。(2&#…...

scscanner:一款功能强大的大规模状态码扫描工具
关于scscanner scscanner是一款功能强大的大规模状态码扫描工具,该工具可以帮助广大研究人员从一个URL列表文件中批量读取目标网站的状态码响应信息。除此之外,该工具还可以过滤出指定的状态码,并将结果存储到一个文件中以供后续深入分析使用…...

Word 和 LaTeX 文档相互转换
Word 和 LaTeX 文档相互转换 目前可以找到两种工具完成将 LaTeX\LaTeXLATEX 文档向 Word 文档的转换, 分别为 Tex2Word和LaTeX-to-Word。 Tex2Word 安装Tex2Word后, 启动 Word, 打开你要转换的 LaTeX\LaTeXLATEX 源文件 (注意,如果没有成功安装 Tex2Word,那么你无法读取…...
python自动发送邮件实现
目录1 前言2 准备工作2.1 电子邮件的基础知识。2.2 python邮件库2.3 邮箱设置3 python实现邮件自动发送3.1 SMTP()和send()方法介绍3.2 python实现实例参考信息1 前言 python功能强大,可以实现我们日常办公的很多任务。诸如批量处理word,excel,pdf等等文件…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...
