计算机网络基本知识（二）
相关文章：
计算机网络基本知识（二）
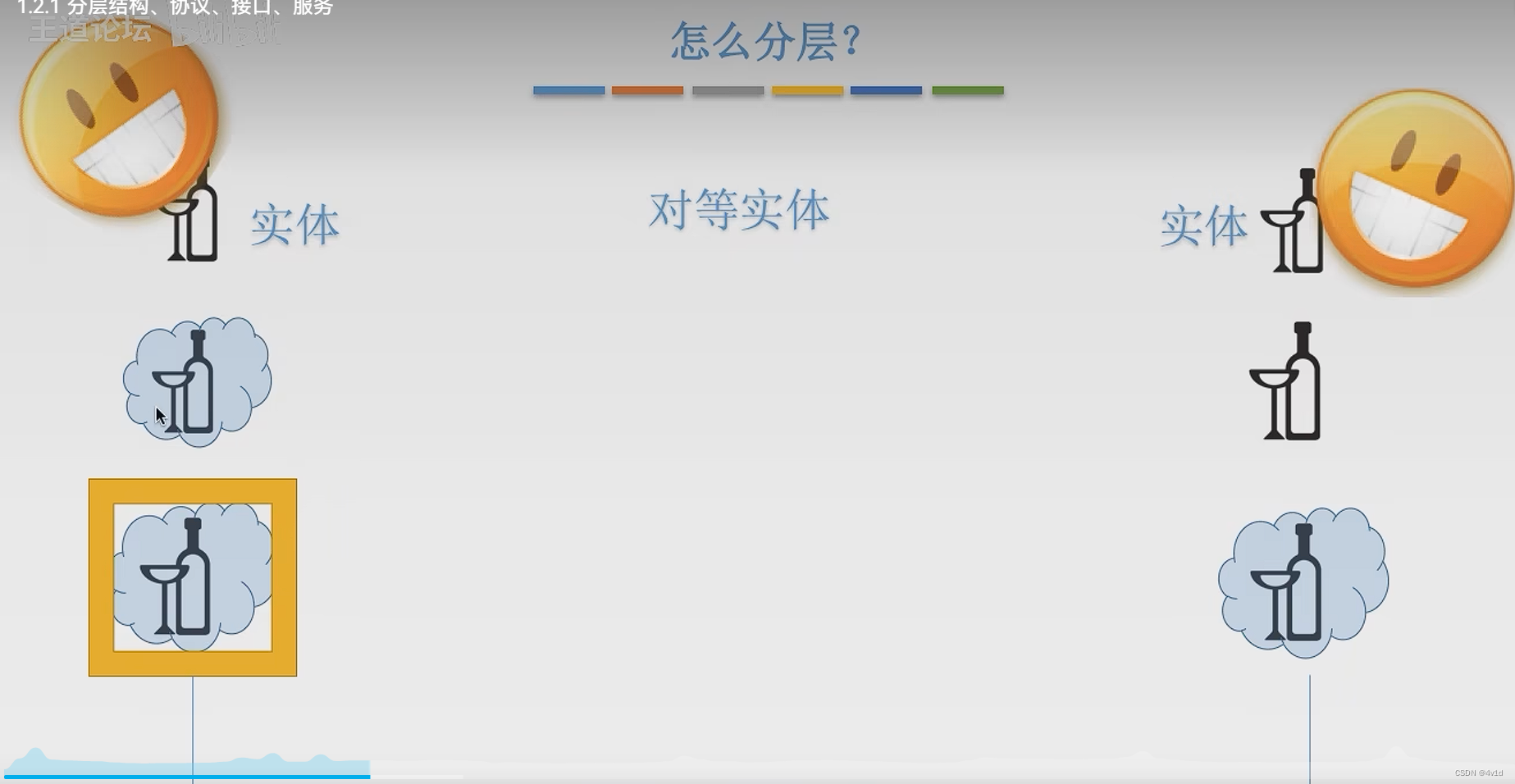
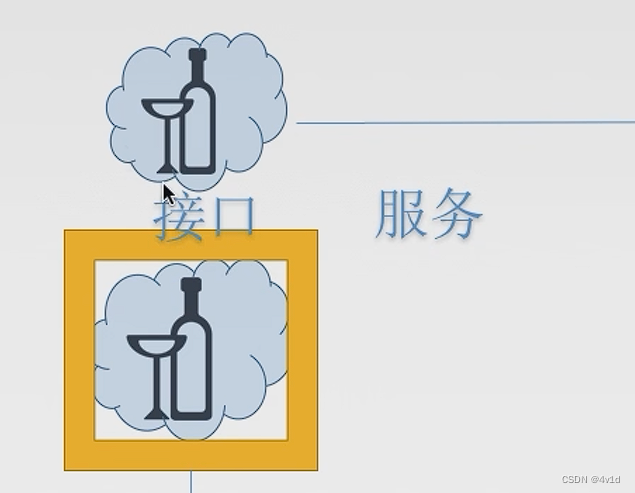
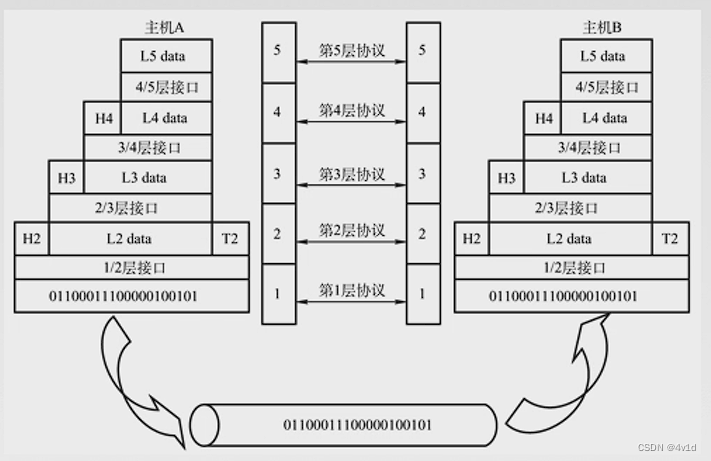
文章目录 概要分层为什么分层怎么分层？1.实体2.协议3.服务 分层基本原则正式认识分层详细例子解释 总结 概要 分层知识：概念理解 分层 为什么分层 大致以上五点 为了解决上面的问题（复杂） 大问题划分为小问题 怎么分层&#…...
158基于matlab的用于分析弧齿锥齿轮啮合轨迹的程序
基于matlab的用于分析弧齿锥齿轮啮合轨迹的程序，输出齿轮啮合轨迹及传递误差。程序已调通，可直接运行。 158 matlab 弧齿锥齿轮啮合轨迹 传递误差 (xiaohongshu.com)...
C#中的浅度和深度复制（C#如何复制一个对象）
文章目录 浅度和深度复制浅度复制深度复制如何选择 浅度和深度复制 在C#中，浅度复制（Shallow Copy）和深度复制（Deep Copy）是两种不同的对象复制方式，满足不同的应用场景需求，它们主要区别在于处…...
2.6日学习打卡----初学RabbitMQ（一）
2.6日学习打卡 初识RabbitMQ、 一. MQ 消息队列 MQ全称Message Queue（消息队列），是在消息的传输过程中保 存消息的容器。多用于系统之间的异步通信。 同步通信相当于两个人当面对话，你一言我一语。必须及时回复 异步通信相当于通…...
Rust语言之集合
文章目录 一、元组（tuple）1.元组定义2.元组使用解构索引 3.元组修改非可变元组可变元组类型不一致 二、数组1.数组不可变数组定义可变数组定义数组使用数组修改数组的遍历 2.动态数组-向量（Vector）向量定义向量遍历向量追加向量插…...
有道论文翻译接口，python版和lua版
论文翻译接口python版 import requests import hashlib from urllib.parse import quotedef get_md5(s,is_hexTrue):md5hashlib.md5()md5.update(s.encode())if is_hex:return md5.hexdigest()return md5.digest()def translate(source_url,from_en,tozh-CHS):params {from: f…...
java大数据hadoop2.9.2 Flume安装操作
1、flume安装 （1）解压缩 tar -xzvf apache-flume-1.9.0-bin.tar.gz rm -rf apache-flume-1.9.0-bin.tar.gz mv ./apache-flume-1.9.0-bin/ /usr/local/flume （2）配置 cd /usr/local/flume/conf cp ./flume-env.sh.template…...
环境配置：Ubuntu18.04 ROS Melodic安装
前言 不同版本的Ubuntu与ROS存在对应关系。 ROS作为目前最受欢迎的机器人操作系统，其核心代码采用C编写，并以BSD许可发布。ROS起源于2007年，是由斯坦福大学与机器人技术公司Willow Garage合作的Switchyard项目。2012年，ROS团队从…...
2024.2.7-8 寒假训练记录（21）
文章目录 洛谷P3193 [HNOI2008] GT考试ATC abc339E Smooth SubsequenceATC abc339F Product Equality 洛谷P3193 [HNOI2008] GT考试 题目链接 KMPdp矩阵快速幂 还没有理解得很清楚，主要是对KMP理解还不够深刻 #include <bits/stdc.h>using namespace std;…...
C++ pair 的使用
pair的作用 C 中的 std::pair 是标准模板库 (STL) 提供的一个容器，它能够存储两个不同类型的数据作为一个整体，其中first：访问 pair 的第一个元素。second：访问 pair 的第二个元素。 int main() {pair<string, int> p;//通…...
AAAI 2024 | Adobe提出全新上下文提示学习框架CoPL，高效提升下游性能
论文题目：CoPL: Contextual Prompt Learning for Vision-Language Understanding 论文链接：https://arxiv.org/abs/2307.00910 提示学习（Prompt Learning）在近几年的快速发展，激活了以Transformer为基础的大型语言模型…...
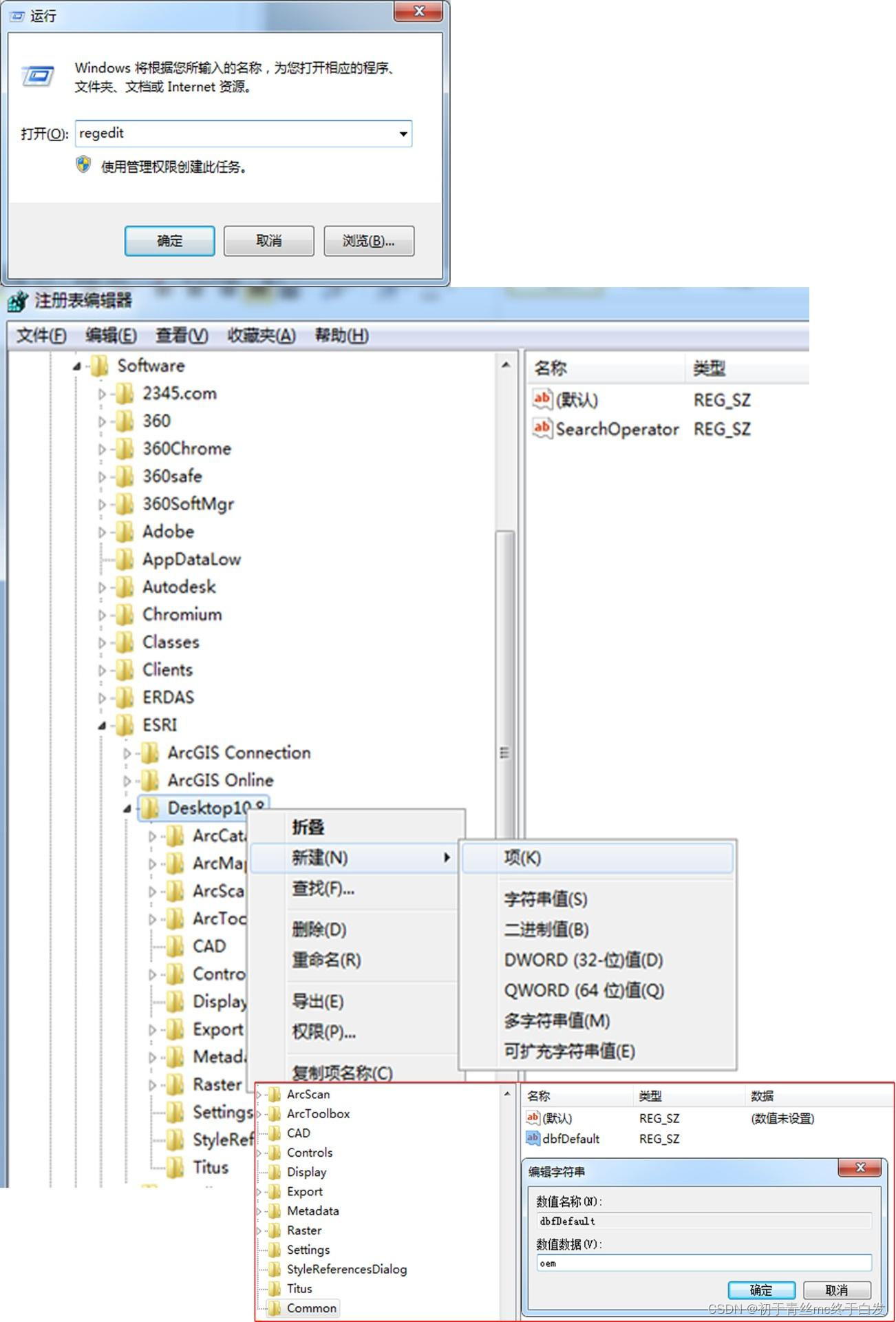
Arcgis使用过程中常见问题解决方法
Arcgis无法连接数据库/数据库连接或创建失败解决方法 最近在使用arcgis过程中出现无法连接数据库或者是无法创建数据库。连接到数据库失败；无法创建新的数据库，权限被拒绝（如下图）。 出现这个原因是你所用的电脑系统文件dao360.…...
office文件转pdf在线预览
一、工具类 package com.sby.utils;import java.io.File; import java.io.FileInputStream; import java.io.FileOutputStream; import java.io.InputStream; import java.math.RoundingMode; import java.text.DecimalFormat; import java.util.Locale;import com.aspose.cel…...
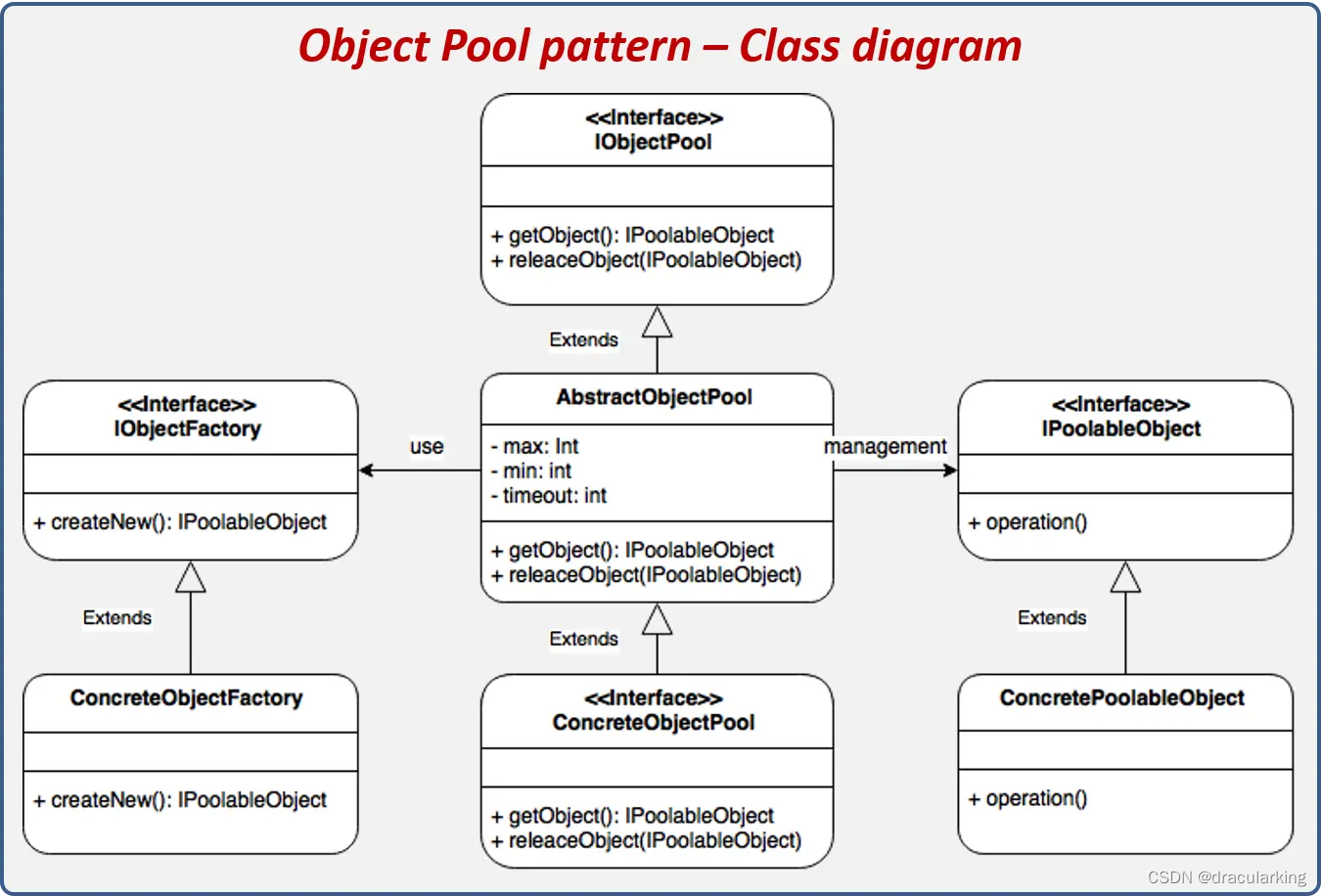
设计模式2-对象池模式
对象池模式，Object Pool Pattern，当你的应用程序需要频繁创建和销毁某种资源（比如数据库连接、线程、socket连接等）时，Object Pool 设计模式就变得很有用。它通过预先创建一组对象并将它们保存在池中，以便在…...
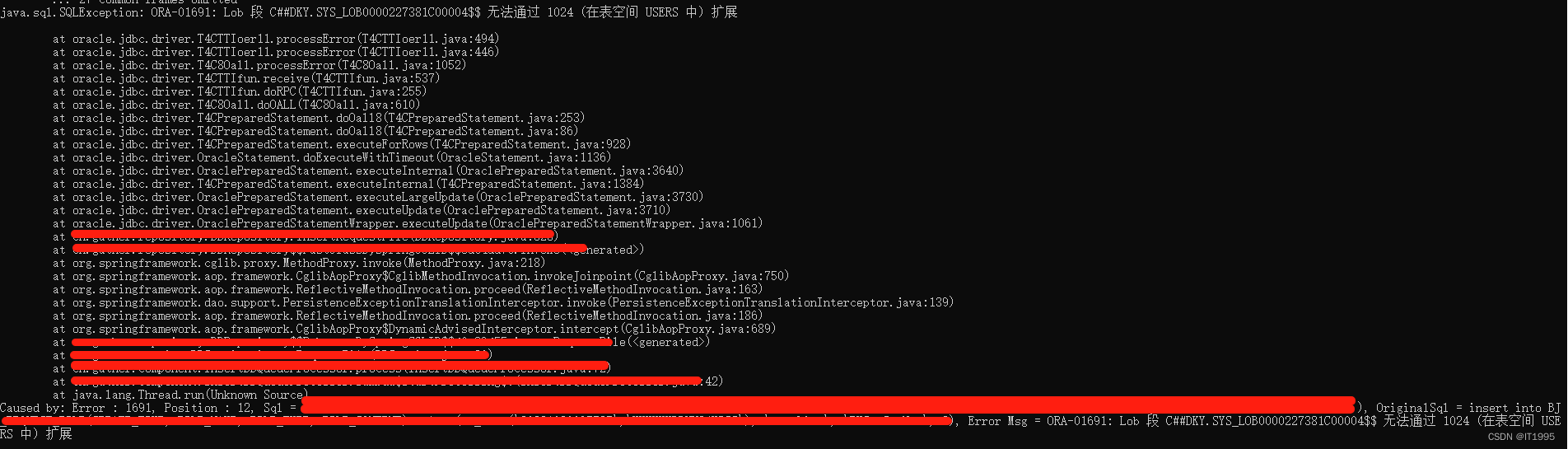
Oracle笔记-为表空间新增磁盘（ORA-01691）
如下报错： 原因是Oracle表空间满了，最好是新增一个存储盘。 #查XXX命名空间目前占用了多大的空间 select FILE_NAME,BYTES/1024/1024 from dba_data_files where tablespace_name XXXX #这里的FILE_NAME能查到DBF的存储位置#将对应的datafile设置为30g…...
【专业技术】高效并行分布式深度学习策略，助力模型训练与量化
尊敬的客户，您好！我们是一家专注于提供高效深度学习解决方案的专业团队，为您提供并行分布式策略、高效精调策略、大模型无损量化和高性能推理服务。 我们的服务包括： 并行分布式策略：我们的Trainer封装支持多种并行配…...
力扣-137. 只出现一次的数字 II
文章目录 力扣题目代码 力扣题目 给你一个整数数组 nums ，除某个元素仅出现 一次 外，其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。 你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。 示例 1：…...
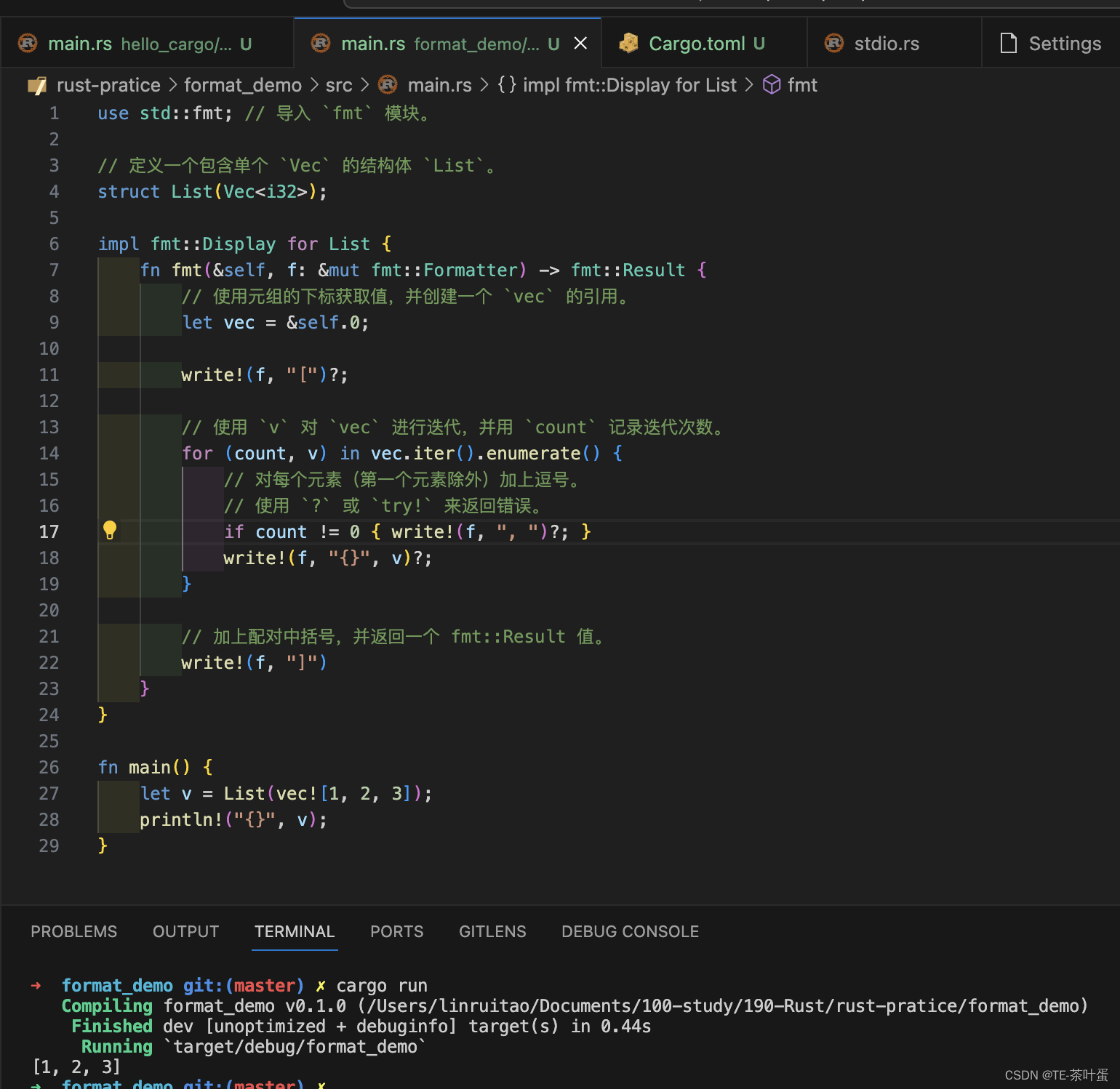
Rust 格式化输出
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 文章目录 前言一、format! 宏二、fmt::Debug三、fmt::Display四、? 操作符 循环打印 前言 Rust学习系列-本文根据教程学习Rust的格式化输出，包括fmt::Debug&…...
c#进程(Process)常用方法
在C#中，Process类提供了一系列用于操作进程的常用方法，以下是其中一些常用的方法： Start()：启动一个新的进程。 Process.Start("notepad.exe");Kill()：终止进程。 Process.GetProcessesByName("note…...
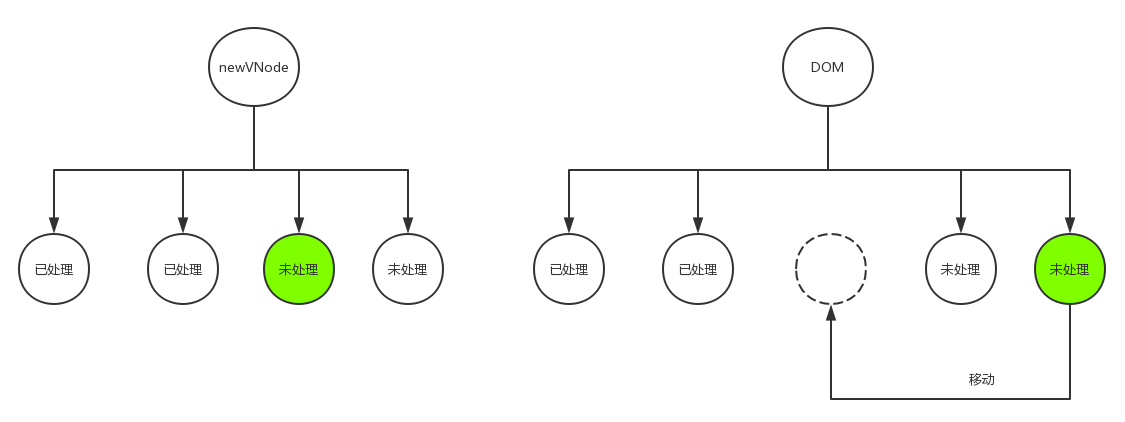
Vue源码系列讲解——虚拟DOM篇【三】(更新子节点)
1. 前言 在上一篇文章中，我们了解了Vue中的patch过程，即DOM-Diff算法。并且知道了在patch过程中基本会干三件事，分别是：创建节点，删除节点和更新节点。创建节点和删除节点都比较简单，而更新节点因为要处理…...
一个设备内存2M，一个1G大小的文件，这个文件有若干行，输出其中的带有hello的行以及行数
第一种 linux上的awk命令： awk {if($1 "113.111.211.224"){print $0}} temp.log 第二种：PHP程序yield ，和awk这个命令用的时间差不多一样，效率是很高的 $file __DIR__."/temp.log";foreach(readfilecong…...
json模块（高维数据的存储与读取）
json模块是 Python 标准库中的一个模块，用于处理 JSON（JavaScript Object Notation）格式的数据。JSON是一种轻量级的数据交换格式，易于人阅读和编写，同时也易于机器解析和生成。模块提供了在 Python 中进行 JSON 编码&…...
ONLYOFFICE文档8.0新功能浅探
ONLYOFFICE文档8.0新功能浅探 上个月末这个月初的几天，ONLYOFFICE版本更新了！更新到了一个比较整的大的版本号，8.0版本，看来这个生产力工具的升级速度基本上能保持每年两个版本号的速度，还是很快的，一般来…...
在vscode 中配置 pyside6 环境
在vscode中编写pyside环境配置 start 记录一下在 vscode 中编写 pyside6 程序，环境如何配置。 前提 请自行安装好 python。请自行安装好 vscode。安装 vscode 插件 Python，PYQT Integration。 配置环境 1.借助 pip 安装我们的pyside6 pip install…...
C语言：月份缩写
题目描述 从一月份到十二月的英文全称依次是：“January”,“February”,“March”,“April”,“May”,“June”,“July”,“August”,“September”,“October”,“November”,“December” 对应的缩写依次是：“Jan.”,“Feb.”,“Mar.”,“Apr.”,“Ma…...
线阵相机系列-- 1. 什么是线阵相机
线阵相机的概念 根据工业相机像素排列方式的不同，分为面阵相机和线阵相机。面阵相机的像素排列为一个完整的面，一次获取整幅二维图像，而线阵相机的像素以一条线排列，每次得到的图像呈现出一条线，通过设置扫描频率以及…...
CISCRISC? CPU架构有哪些? x86 ARM？
编者按：鉴于笔者水平有限，文中难免有不当之处，还请各位读者海涵。 是为序 我猜，常年混迹CSDN的同学应该不会没听说过CPU吧？ 但你真的了解CPU吗？那笔者问你CPU有哪些架构呢？ 如果你对你的答案…...
【C语言】（15）指针进阶
1. 指针与const 在C语言中，const关键字和指针一起使用时，可以创建对常量的引用，或者创建指向常量的指针。这对于保护重要数据不被意外修改以及提高程序的可读性和运行时的安全性非常有用。 1.1 const的基本用法 const关键字用于声明一个变…...
力扣精选算法100道—— 连续数组（前缀和专题）
连续数组（前缀和专题） 目录 🚩了解题意 🚩算法原理 ❗为什么hash设置成<0,-1>键值对 ❗与和为K的子数组比较hash的键值对 🚩代码实现 🚩了解题意 我们看到给定数组里面只有0和1，我们…...
flutter 国内源
Flutter 在中国由于网络原因，从官方默认的国外源下载Dart包和Flutter SDK可能会比较慢或者不稳定。为了加速依赖包的获取与Flutter SDK的安装，可以使用国内镜像源。以下是一些国内常用的Flutter和Dart包镜像源： 清华大学开源软件镜像站 Flu…...
第九个知识点：内部对象
Date对象: <script>var date new Date();date.getFullYear();//年date.getMonth();//月date.getDate();//日date.getDay();//星期几date.getHours();//时date.getMinutes();//分date.getSeconds();//秒date.getTime();//获取时间戳，时间戳时全球统一&#x…...
Android 车载应用开发之车载操作系统
一、前言 到 2030 年，全球电动汽车的销量将超过 7000 万辆，保有量将达到 3.8 亿辆，全球年度新车渗透率有望触及 60% 。这一数据来自国际能源署（IEA）发布的《全球电动汽车展望2023》。 市场趋势和政策努力的双加持下，新能源汽车来势凶猛，燃油车保有量逐年递减。此番景象…...
Qt PCL学习（文章链接汇总）
Qt PCL学习（一）：环境搭建 Qt PCL学习（二）：点云读取与保存 Qt PCL学习（三）：点云滤波 Qt PCL学习（四）：点云关键点 持续更新中…...
安卓动态链接库文件体积优化探索实践
背景介绍 应用安装包的体积影响着用户下载量、安装时长、用户磁盘占用量等多个方面，据Google Play统计，应用体积每增加6MB，安装的转化率将下降1%。 安装包的体积受诸多方面影响，针对dex、资源文件、so文件都有不同的优化策略&…...
[Java][算法 哈希]Day 01---LeetCode 热题 100---01~03
LeetCode 热题 100---01~03 ------->哈希 第一题 两数之和 思路 最直接的理解就是 找出两个数的和等于目标数 这两个数可以相同 但是不能是同一个数字（从数组上理解就是内存上不是同一位置） 解法一：暴力法 暴力解万物 按照需求 …...
【每日一题】LeetCode——链表的中间结点
📚博客主页：爱敲代码的小杨. ✨专栏：《Java SE语法》 | 《数据结构与算法》 | 《C生万物》 ❤️感谢大家点赞👍🏻收藏⭐评论✍🏻，您的三连就是我持续更新的动力❤️ 🙏小杨水平有…...
k8s 部署java应用 基于ingress+jar包
k8 集群ingress的访问模式 先部署一个namespace 命名空间 vim namespace.yaml kind: Namespace apiVersion: v1 metadata:name: ingress-testlabels:env: ingress-test 在部署deployment deployment是pod层一层封装。可以实现多节点部署 资源分配 回滚部署等方式。 部署的…...
深度学习技巧应用36-深度学习模型训练中的超参数调优指南大全,总结相关问题与答案
大家好，我是微学AI，今天给大家介绍一下深度学习技巧应用36-深度学习模型训练中的超参数调优指南大全,总结相关问题与答案。深度学习模型训练中的调优指南大全概括了数据预处理、模型架构设计、超参数优化、正则化策略和训练技巧等多个关键方面，以提升模型性能和泛化能力。 …...
“探索AJAX：前端与后端数据交互的利器“
前言 在现代Web开发中，前端与后端之间的数据交互是一个至关重要的环节。为了实现无需刷新页面的动态更新，AJAX（Asynchronous JavaScript and XML）作为一种强大的技术被广泛应用。 AJAX的原理 AJAX通过JavaScript和XMLHttpReque…...
【5G NR】移动通讯中使用的信道编解码技术
目录 一、引言 二、信道编解码技术概述 三、移动通讯中常用的信道编解码技术 四、优缺点分析与比较 五、未来发展趋势 六、结论 本文主要介绍了移动通讯中采用的信道编解码技术，由于在5G NR终端中，通常要兼容4G LTE通讯技术，所以4G LTE…...
用Python Tkinter打造的精彩连连看小游戏【附源码】
文章目录 连连看小游戏：用Python Tkinter打造的精彩游戏体验游戏简介技术背景MainWindow类:职责:方法:Point类: 主执行部分:完整代码：总结： 连连看小游戏：用Python Tkinter打造的精彩游戏体验 在丰富多彩的游戏世界中，…...
nvm安装node后，npm无效
类似报这种问题，是因为去github下载npm时下载失败， Please visit https://github.com/npm/cli/releases/tag/v6.14.17 to download npm. 第一种方法：需要复制这里面的地址爬梯子去下载（github有时不用梯子能直接下载，有…...
spring boot(2.4.x 开始)和spring cloud项目中配置文件application和bootstrap加载顺序
在前面的文章基础上 https://blog.csdn.net/zlpzlpzyd/article/details/136060312 spring boot 2.4.x 版本之前通过 ConfigFileApplicationListener 加载配置 https://github.com/spring-projects/spring-boot/blob/v2.3.12.RELEASE/spring-boot-project/spring-boot/src/mai…...
5-2、S曲线计算【51单片机+L298N步进电机系列教程】
↑↑↑点击上方【目录】，查看本系列全部文章 摘要：本节介绍S曲线的基本变换，将基本形式的S曲线变换成为任意过两点的S曲线，为后续步进电机S曲线运动提供理论支撑 一.计算目标 ①计算经过任意不同两点的S曲线方程 ②可调节曲线平…...
SQL 注入 - http头注入之UA头注入探测
环境准备：构建完善的安全渗透测试环境：推荐工具、资源和下载链接_渗透测试靶机下载-CSDN博客 一、http头注入介绍 HTTP头注入是一种网络安全攻击手段，它利用了Web应用程序对HTTP头的处理不当或缺乏充分的验证和过滤。在这种攻击中，攻击者通过修改HTTP请求头中的某些字段，…...
学习数据结构和算法的第5天
空间复杂度及其常见案例 空间复杂度 空间复杂度也是一个数学函数表达式，是对一个算法在运行过程中临时占用存储空间大小的量度。 空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。空间复杂度…...
Android 11 访问 Android/data/或者getExternalCacheDir() root方式
前言： 需求要求安装三方应用ExternalCacheDir()下载下来的apk文件。 getExternalCacheDir() : /storage/emulated/0/Android/data/com../cache/ 获取访问权限 如果手机安卓版本为Android10的时候,可以在AndroidManifest.xml中添加下列代码 android:requestLegacyExt…...
Linux探秘之旅：透彻理解路径、命令与系统概念
目录 如何远程连接 远程登录简明指南 linux区别 1.严格区分大小写 2.linux的命令返回结果判断 3.如何查看网络信息 4.关于后缀名（Linux不关心文件后缀） 4.1 需要记忆的后缀 5.echo命令 6.linux一切皆文件 6.1比如磁盘的文件 6.2可执行文件 …...
哈希算法 c语言
#include <stdio.h> #include <stdlib.h> #include <string.h> // 哈希函数 unsigned int hash_function(const char *str) { unsigned int hash 0; while (*str) { hash (hash * 31 *str) % 1000; str; } return hash;…...
新版MQL语言程序设计：组合模式的原理、应用及代码实现
文章目录 一、什么组合模式二、为什么需要组合模式三、组合模式的实现原理四、组合模式的应用场景五、组合模式的代码实现 一、什么组合模式 组合模式是一种结构型设计模式，它允许将对象组合成树形结构以表示“部分-整体”的层次结构。组合模式使得用户对单个对象和…...