wyh的迷宫
涉及知识点:求迷宫能否到达终点的,而不是求路径数的,用bfs时可以不用重置状态数组(回溯)。
题目描述
给你一个n*m的迷宫,这个迷宫中有以下几个标识:
s代表起点
t代表终点
x代表障碍物
.代表空地
现在你们涵哥想知道能不能从起点走到终点不碰到障碍物(只能上下左右进行移动,并且不能移动到已经移动过的点)。
输入描述:
输入第一行一个整数T(1<=T<=10) 接下来有T组测试数据,对于每一组测试数据,第一行输入2个数n和m(1<=n,m<=500) 接下来n行,每行m个字符代表这个迷宫,每个字符都是上面4个中的一种 数据保证只有一个起点和一个终点
输出描述:
对于每一组测试数据,如果可以的话输出YES,不可以的话输出NO
示例1
输入
复制1 3 5 s...x x...x ...tx
1 3 5 s...x x...x ...tx
输出
复制YES
YES
想法:
用dfs求,结果超时了。毕竟都500层了……
代码:
#include<bits/stdc++.h>
using namespace std;
int n,m;
int ans;
char mg[510][510];
int a,b;//终点
int dx[]={0,0,1,-1};
int dy[]={1,-1,0,0};
int st[510][510];
void dfs(int x,int y){
for(int i=0;i<4;i++){
int xx=dx[i]+x;
int yy=dy[i]+y;
if(xx<1||yy<1||xx>n||yy>m) continue;
if(mg[xx][yy]=='x') continue;
if(st[xx][yy]) continue;
if(xx==a&&yy==b) {ans++; return;}
st[xx][yy]=1;
dfs(xx,yy);
st[xx][yy]=0;
}
}
int main(){
int t;
cin>>t;
while(t--){
memset(st,0,sizeof(st));
ans=0;
cin>>n>>m;
int x,y;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>mg[i][j];
if(mg[i][j]=='s') { x=i,y=j;}
if(mg[i][j]=='t') { a=i,b=j;}
}
}
dfs(x,y);
if(ans) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
return 0 ;
}
想法:
今天看网课,讲到bfs的时间复杂度要比dfs小(其实是回溯了的dfs时间复杂度才比bfs大很多),所以就试试bfs的写法,过了。还学到了一个小技巧,队列中的坐标的存储可以不用数对pair,用一个数值表示。

代码:
#include<bits/stdc++.h>
using namespace std;
int n,m;
int ans;
char mg[510][510];
int dx[]={0,0,1,-1};
int dy[]={1,-1,0,0};
int st[510][510];
queue <int> q;
void bfs(int x,int y){
q.push(x*m+y);
while(!q.empty()){
int a=q.front()/m;
int b=q.front()%m;
q.pop();
for(int i=0;i<4;i++){
int xx=a+dx[i];
int yy=b+dy[i];
if(mg[xx][yy]=='x') continue;
if(mg[xx][yy]=='t') { ans=1;break;}//到终点
if(st[xx][yy]) continue;
if(xx>=n||xx<0||yy<0||yy>=m) continue;
st[xx][yy]=1;
q.push(xx*m+yy);
}
if(ans==1) return ;
}
}
int main(){
int t;
cin>>t;
while(t--){
memset(st,0,sizeof(st));
ans=0;
cin>>n>>m;
int x,y;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
cin>>mg[i][j];
if(mg[i][j]=='s') { x=i,y=j;}
}
}
st[x][y]=1;
bfs(x,y);
if(ans) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
return 0 ;
}
事情到这并没有结束,我写完就去翻了一下别人的题解,发现其实也可以用dfs写出来,我们不需要具体路径,只需要知道起点终点是否连通(我本来想用连通块写的,但感觉还是会超时,就否决了),因此,本题不用回溯也不可以回溯,回溯会超时。这么做时间复杂度和上一个bfs的时一样的,就是全部格子都搜了一遍,时间复杂度为O(n*m)。
代码:
#include<bits/stdc++.h>
using namespace std;
int n,m;
int ans;
char mg[510][510];
int a,b;//终点
int dx[]={0,0,1,-1};
int dy[]={1,-1,0,0};
int st[510][510];
void dfs(int x,int y){
for(int i=0;i<4;i++){
int xx=dx[i]+x;
int yy=dy[i]+y;
if(xx<1||yy<1||xx>n||yy>m) continue;
if(mg[xx][yy]=='x') continue;
if(st[xx][yy]) continue;
if(xx==a&&yy==b) {ans++; return;}
st[xx][yy]=1;
dfs(xx,yy);
//st[xx][yy]=0;
}
}
int main(){
int t;
cin>>t;
while(t--){
memset(st,0,sizeof(st));
ans=0;
cin>>n>>m;
int x,y;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>mg[i][j];
if(mg[i][j]=='s') { x=i,y=j;}
if(mg[i][j]=='t') { a=i,b=j;}
}
}
dfs(x,y);
if(ans) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
return 0 ;
}
嗐,其实还是感觉怪怪的,再想想吧。
相关文章:

wyh的迷宫
涉及知识点:求迷宫能否到达终点的,而不是求路径数的,用bfs时可以不用重置状态数组(回溯)。 题目描述 给你一个n*m的迷宫,这个迷宫中有以下几个标识: s代表起点 t代表终点 x代表障碍物 .代…...
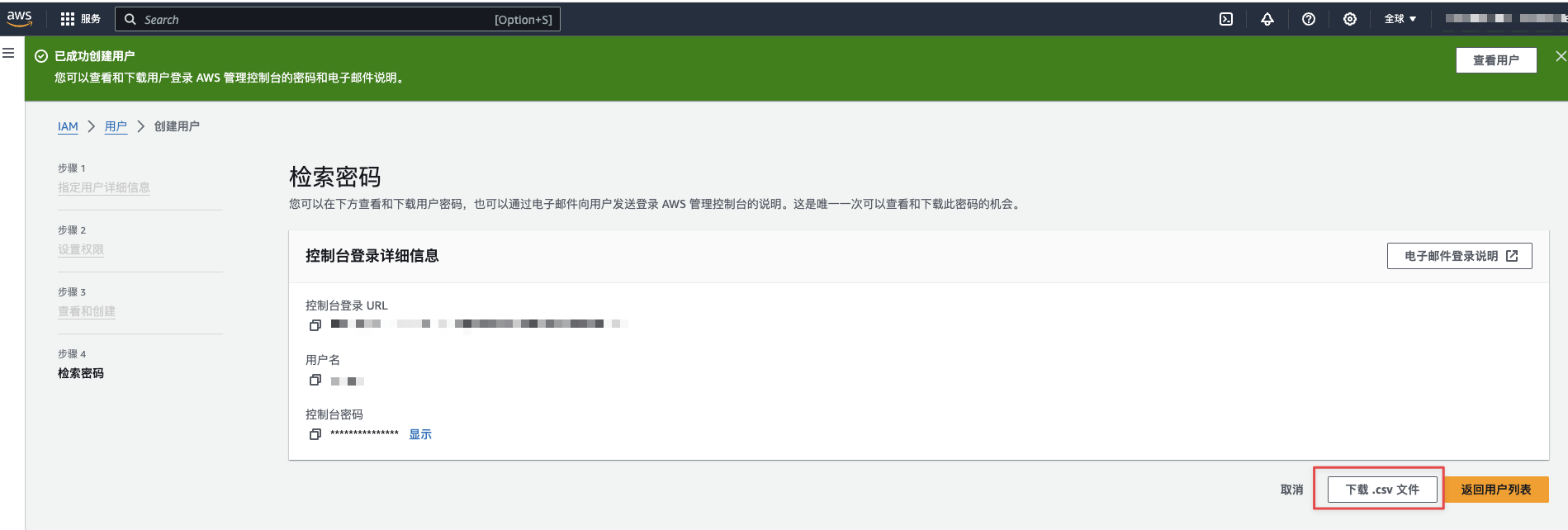
AWS云用户创建
问题 需要给工友创建AWS云的用户,这里假设使用分配给自己AWS开发者IAM账号,给别人创建aws IAM账号。 登录系统 打开页面:https://xxx.signin.aws.amazon.com/console,使用分配的开发者账号登录。如下图: 创建用户…...
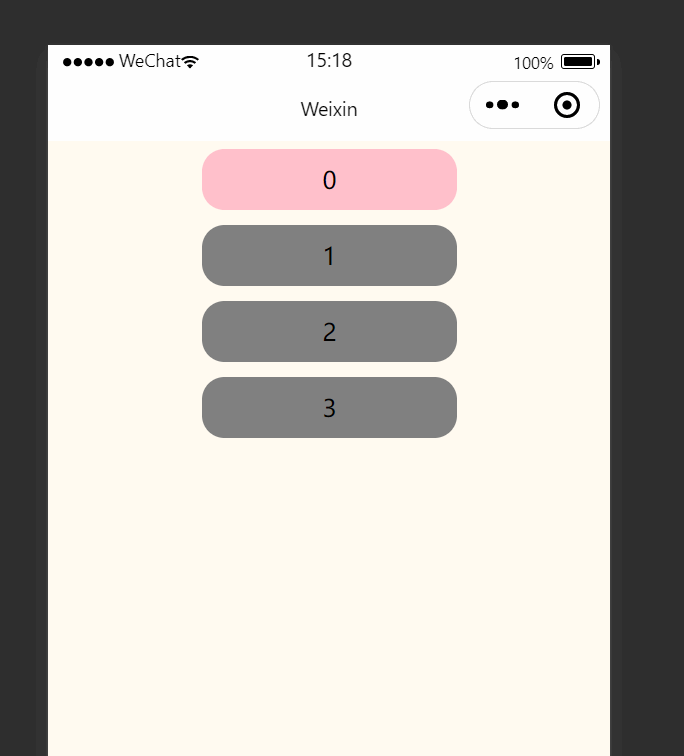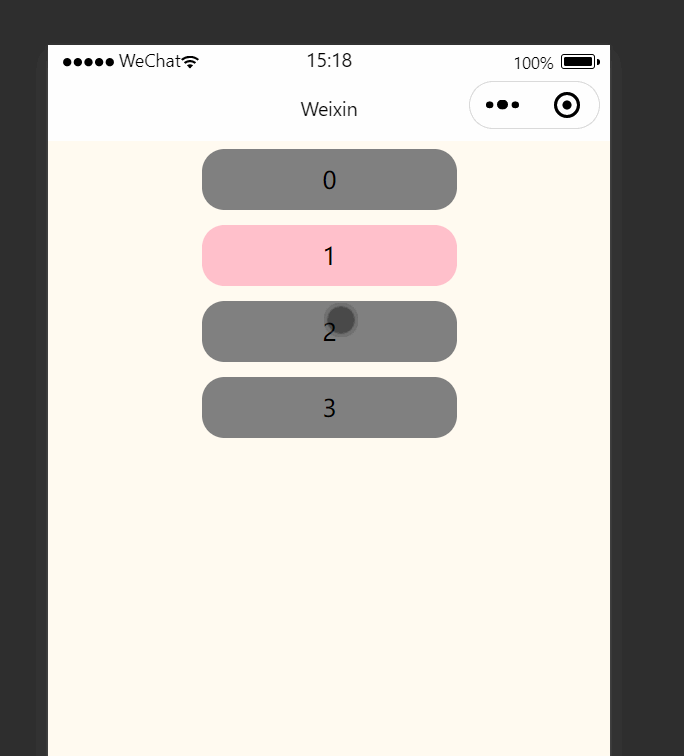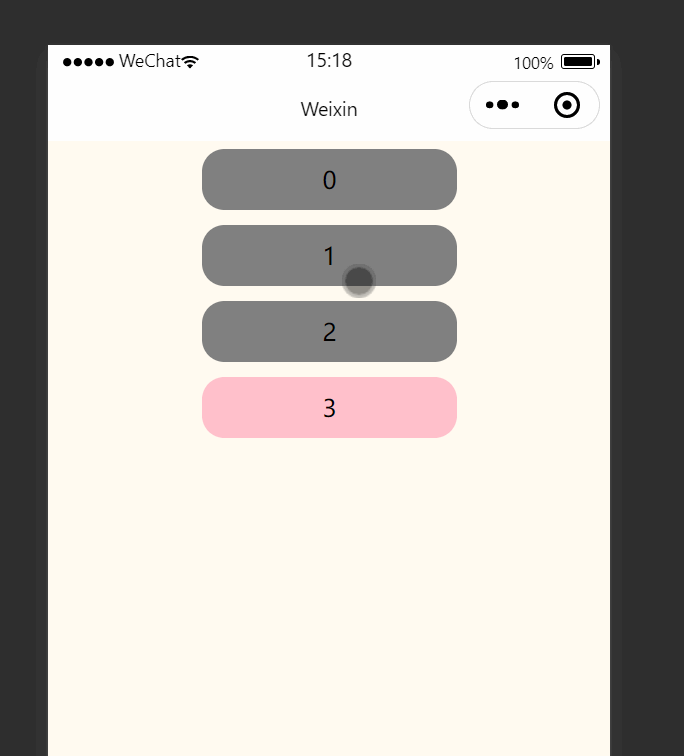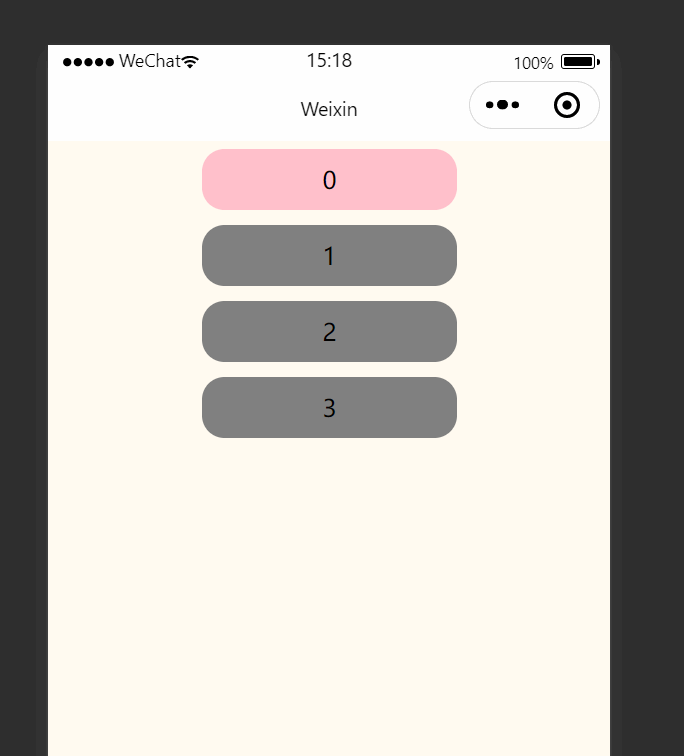
微信小程序(三十七)选项点击高亮效果
注释很详细,直接上代码 上一篇 新增内容: 1.选择性渲染类 2.以数字为需渲染内容(数量) 源码: index.wxml <view class"Area"><!-- {{activeNumindex?Active:}}是选择性添加类名进行渲染 -->&l…...
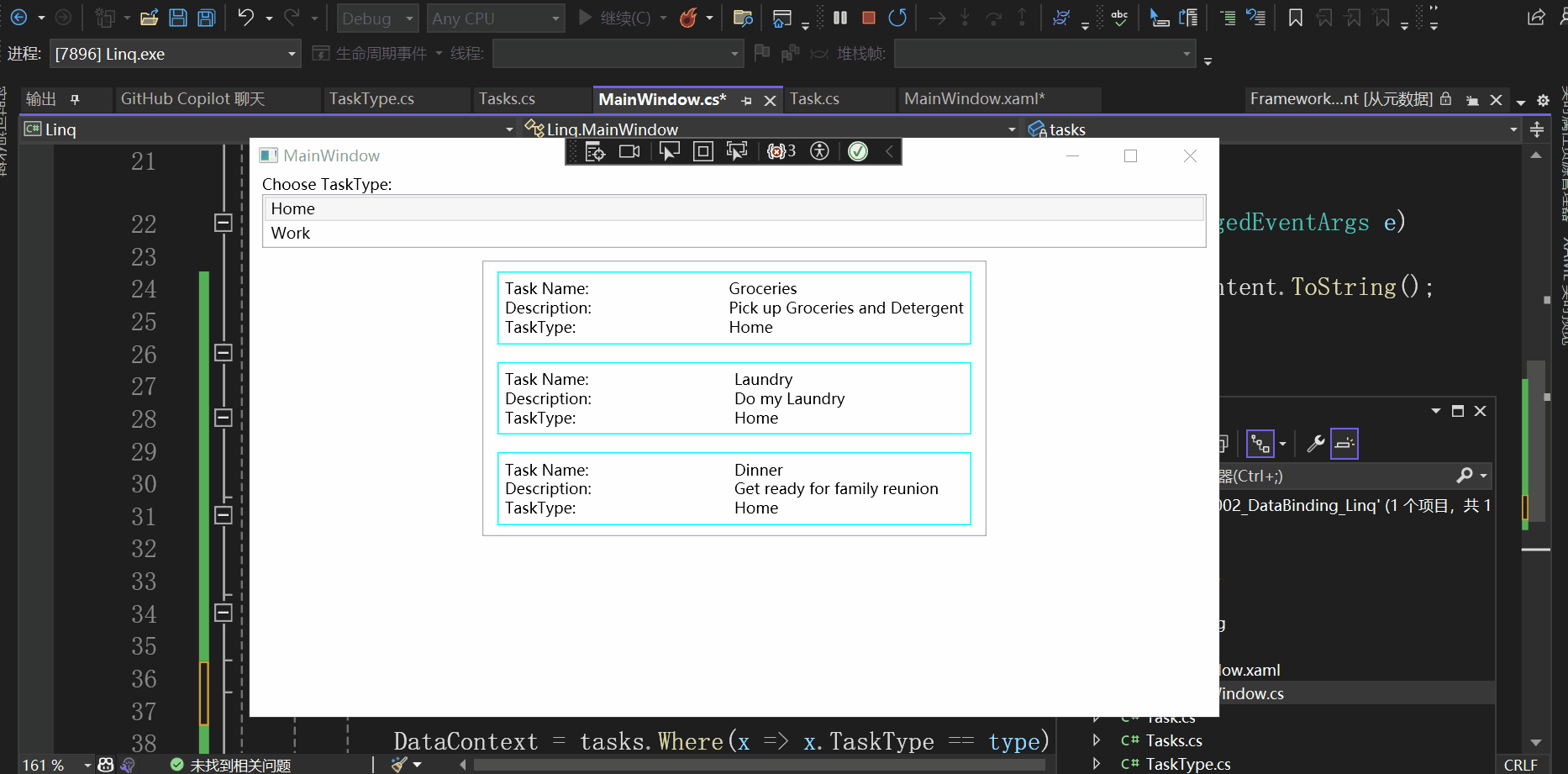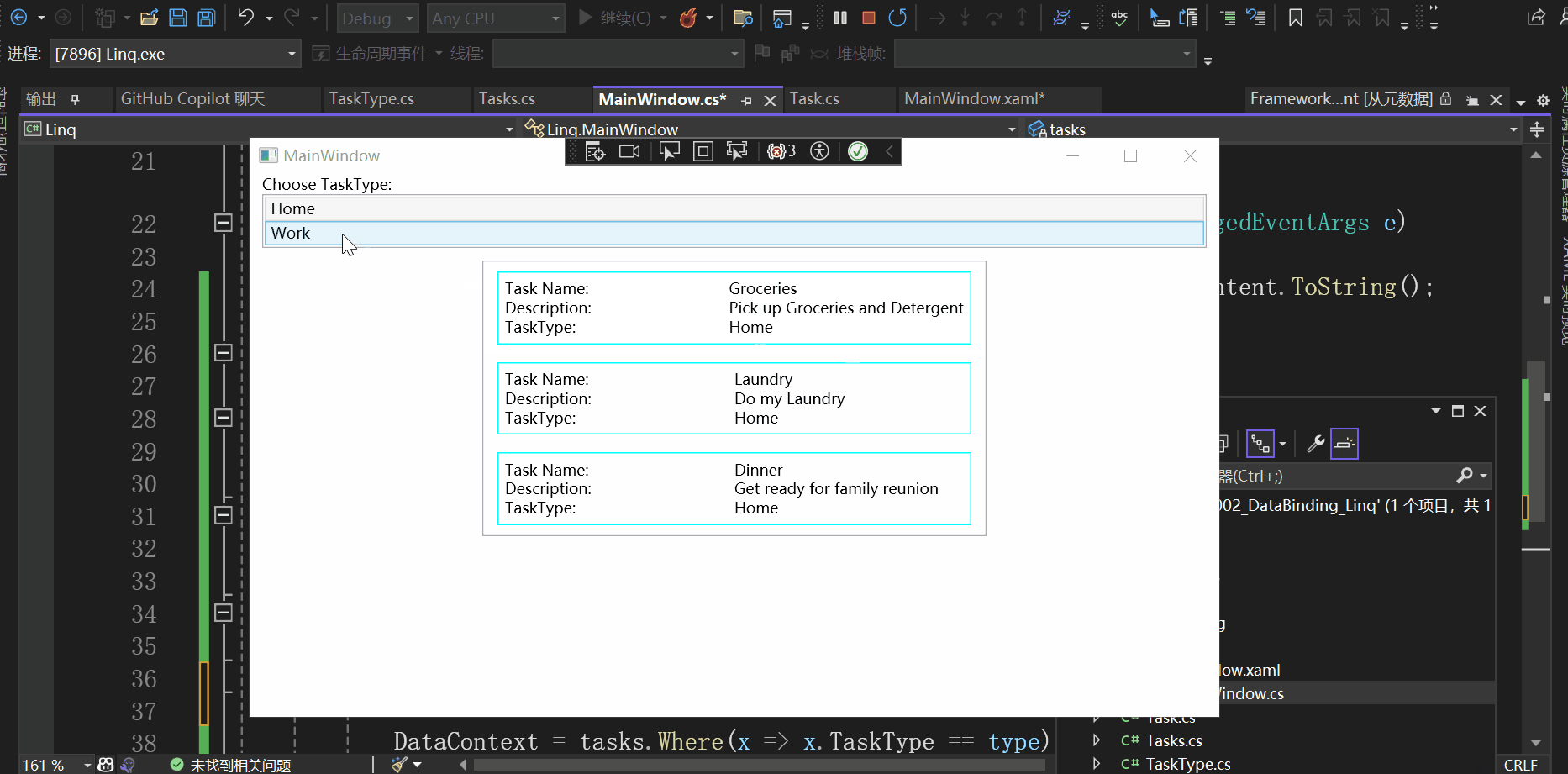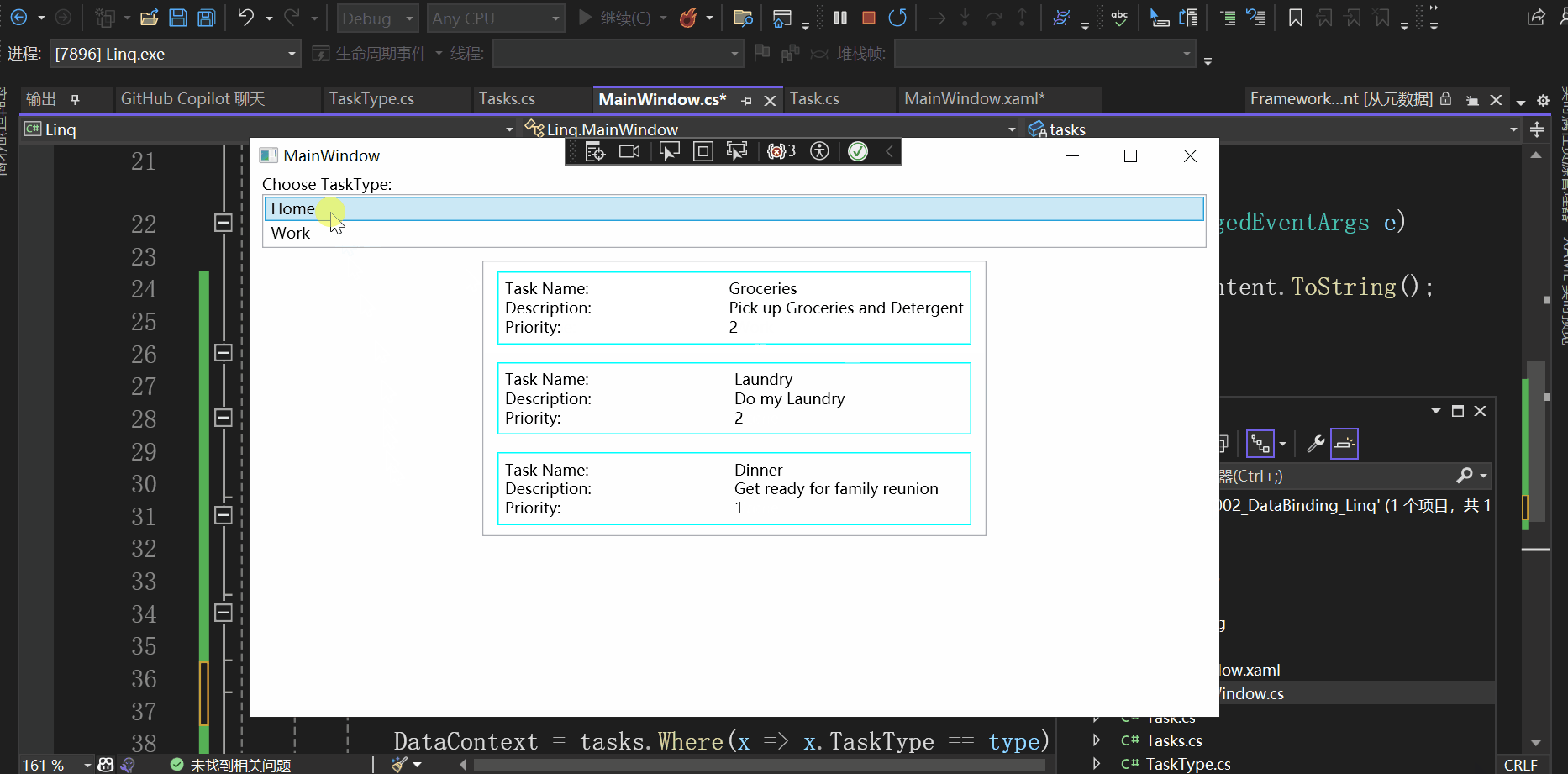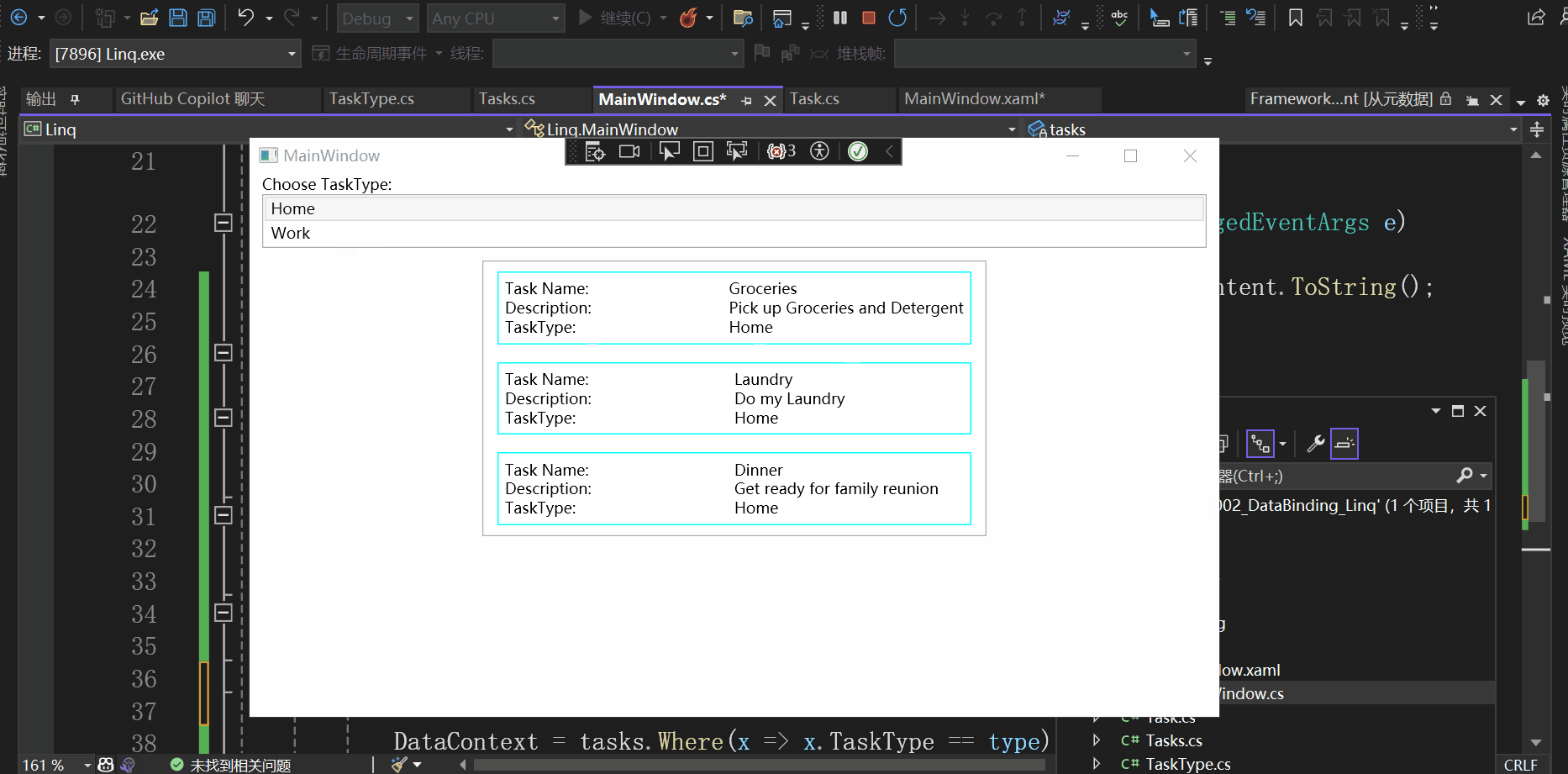
通过Demo学WPF—数据绑定(二)
准备 今天学习的Demo是Data Binding中的Linq: 创建一个空白解决方案,然后添加现有项目,选择Linq,解决方案如下所示: 查看这个Demo的效果: 开始学习这个Demo xaml部分 查看MainWindow.xaml: …...
数据湖的整体思路
湖本质上是一个集中化,中心化的,一体化的存储技术,并且在其之上追求技术架构的统一化,如流批一体,服务分析一体化。 当数据湖成为中心,那么就可以围湖而建“数据服务环”,环上的服务包括了数仓、…...

51单片机 跑马灯
#include <reg52.h>//毫秒级延时函数 void delay(int z) {int x,y;for(x z; x > 0; x--)for(y 114; y > 0 ; y--); }sbit LED1 P1^0x0; sbit LED2 P1^0x1; sbit LED3 P1^0x2; sbit LED4 P1^0x3; sbit LED5 P1^0x4; sbit LED6 P1^0x5; sbit LED7 P1^0x6; s…...

迎新年年终总结
迎新年年终总结 1、除夕迎新年登高有感 1、除夕迎新年登高有感 除旧岁,迎新年。凭栏立,意阑珊。 天空阔,世道艰。唯自强,可彼岸。 于2024年2月9日 10:51。...

一台服务器可以支持多少TCP连接
前言 在linux系统中一切皆文件,每当有一个tcp连接建立,那么就会打开一个文件描述符。在Linux系统中,文件描述符打开的个数是有限制的,当超过这个限制的时候内核就会跑出too many open files异常。 linux上能打开的最大文件…...
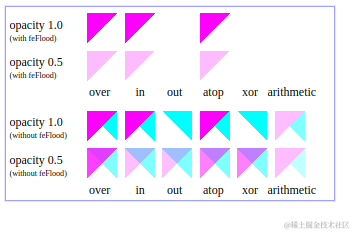
svg基础(六)滤镜-图像,光照效果(漫反射,镜面反射),组合
1 feImage:图像滤镜 feImage 滤镜从外部来源取得图像数据,并提供像素数据作为输出(意味着如果外部来源是一个 SVG 图像,这个图像将被栅格化。) 1.1 用法: <feImage x"" y"" width"&quo…...
电脑数据误删如何恢复?9 个Windows 数据恢复方案
无论您是由于软件或硬件故障、网络犯罪还是意外删除而丢失数据,数据丢失都会带来压力和令人不快。 如今的企业通常将其重要数据存储在云或硬盘上。但在执行其中任何一项操作之前,您很有可能会丢失数据。 数据丢失的主要原因是意外删除,任何…...
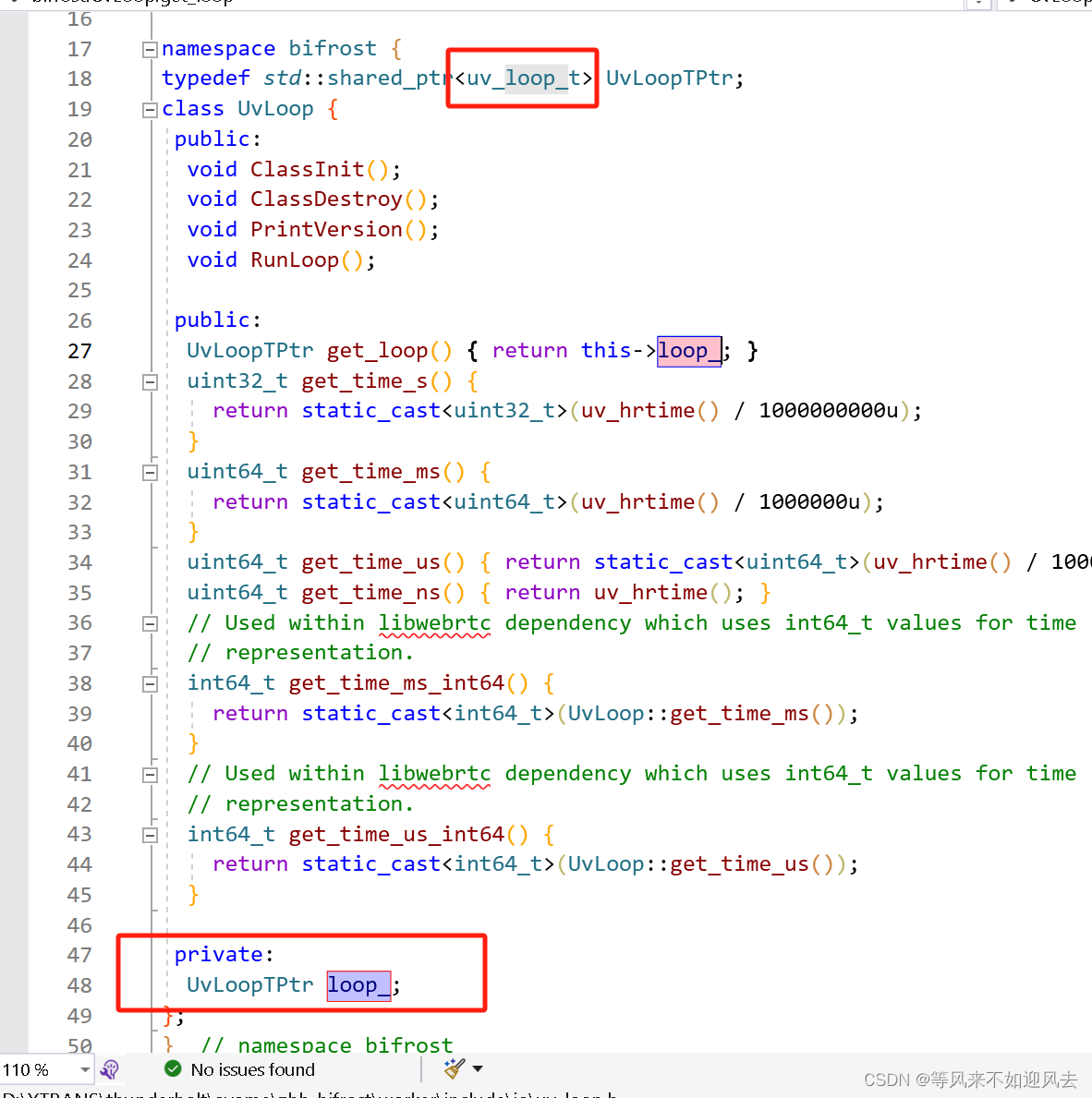
【doghead】uv_loop_t的创建及线程执行
worker测试程序,类似mediasoup对uv的使用,是one loop per thread 。创建一个UVLoop 就可以创建一个uv_loop_t Transport 创建一个: 试验配置创建一个: UvLoop 封装了libuv的uv_loop_t ,作为共享指针提供 对uv_loop_t 创建并初始化...
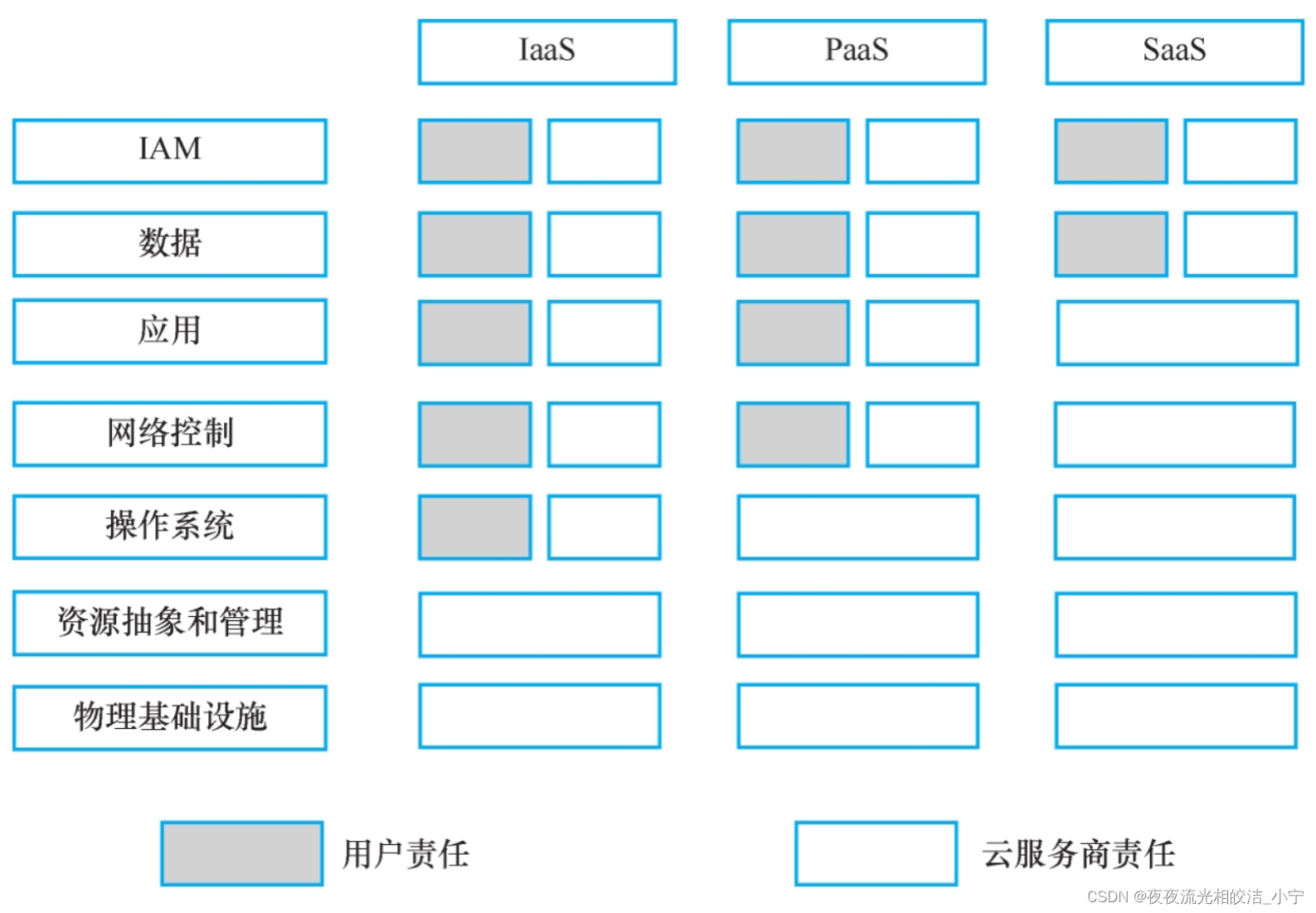
云计算运营模式介绍
目录 一、云计算运营模式概述 1.1 概述 二、云计算服务角色 2.1 角色划分 2.1.1 云服务提供商 2.1.2 云服务消费者 2.1.3 云服务代理商 2.1.4 云计算审计员 2.1.5 云服务承运商 三、云计算责任模型 3.1 云计算服务模式与责任关系图 3.2 云计算服务模式与责任关系解析…...
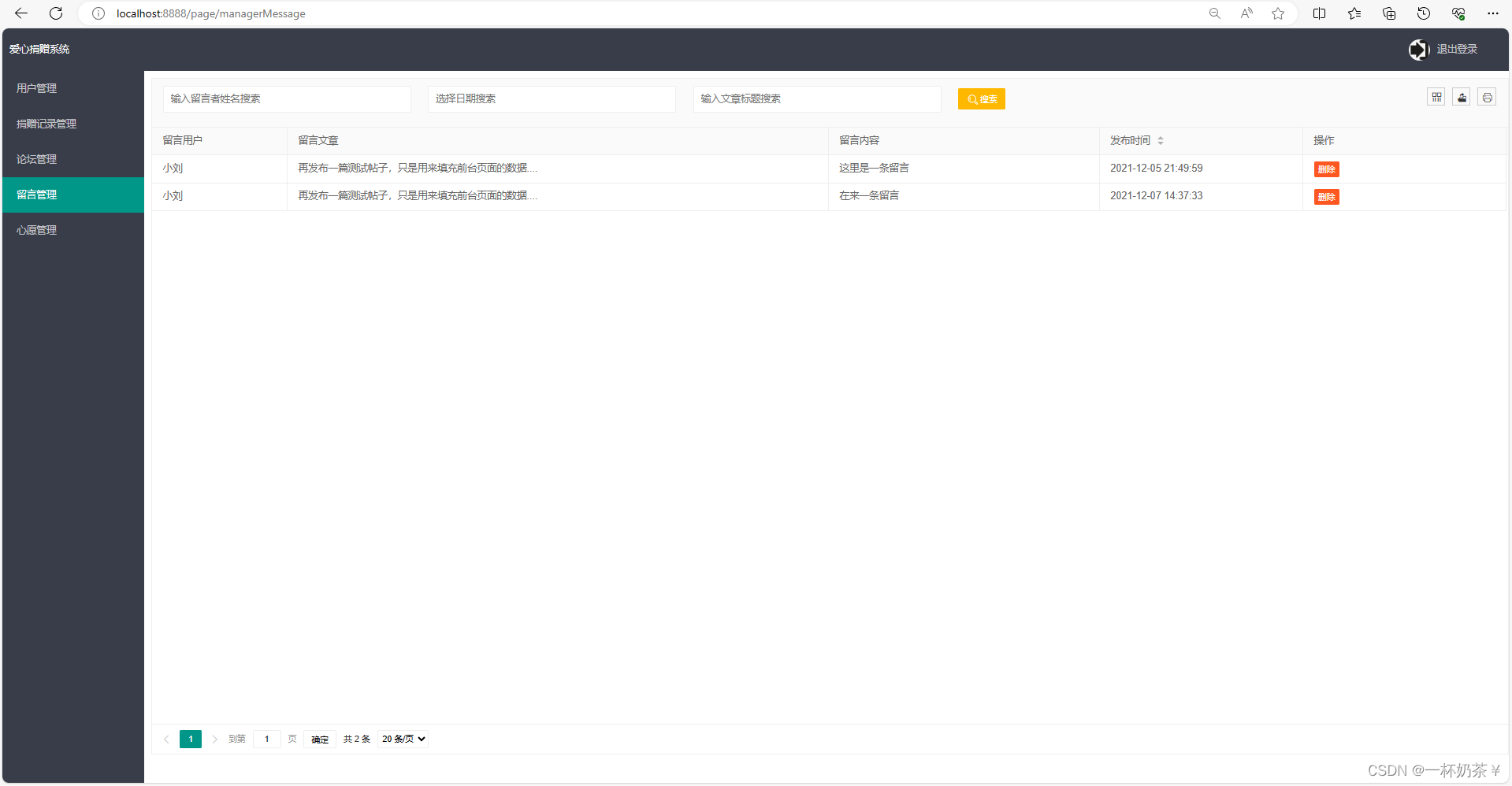
物资捐赠管理系统
文章目录 物资捐赠管理系统一、项目演示二、项目介绍三、系统部分功能截图四、部分代码展示五、底部获取项目(9.9¥带走) 物资捐赠管理系统 一、项目演示 爱心捐赠系统 二、项目介绍 基于springboot的爱心捐赠管理系统 开发语言:…...
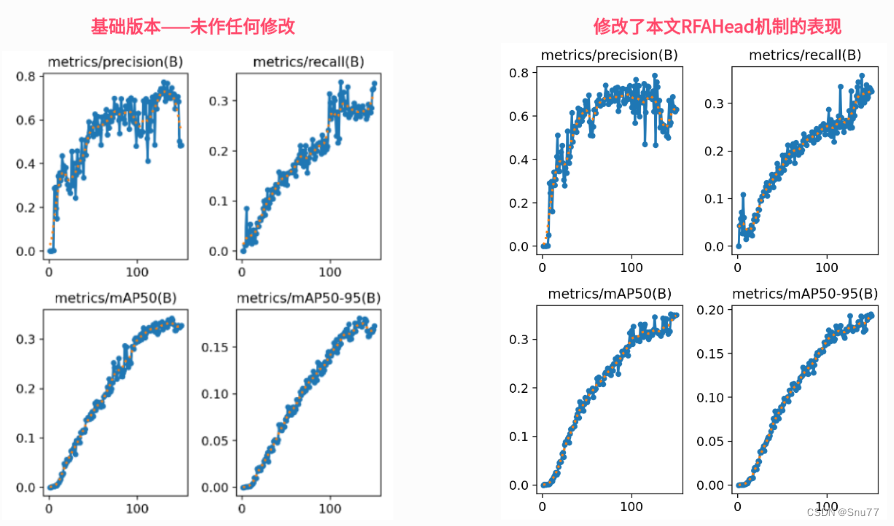
YOLOv8改进 | 检测头篇 | 独创RFAHead检测头超分辨率重构检测头(适用Pose、分割、目标检测)
一、本文介绍 本文给大家带来的改进机制是RFAHead,该检测头为我独家全网首发,本文主要利用将空间注意力机制与卷积操作相结合的卷积RFAConv来优化检测头,其核心在于优化卷积核的工作方式,特别是在处理感受野内的空间特征时。RFAConv主要的优点就是增加模型的特征提取能力,…...
私有化部署一个吃豆人小游戏
目录 效果 安装步骤 1.安装并启动httpd 2.下载代码 3.启动httpd 使用 效果 安装步骤 1.安装并启动httpd yum -y install httpd 2.下载代码 进入目录 cd /var/www/html/ 下载 git clone https://gitee.com/WangZhe168_admin/pacman-canvas.git 3.启动httpd syste…...

社区店经营管理新思路:提升业绩的秘诀
作为一名资深的鲜奶吧创业者,我深知在社区经营一家店铺所面临的挑战与机遇。经过5年的探索与实践,我总结出了一套提升社区店业绩的秘诀,今天就和大家分享一下。 一、明确目标客户群体,精准定位 在社区开店,首先要明确…...

统一数据格式返回,统一异常处理
目录 1.统一数据格式返回 2.统一异常处理 3.接口返回String类型问题 1.统一数据格式返回 添加ControllerAdvice注解实现ResponseBodyAdvice接口重写supports方法,beforeBodyWrite方法 /*** 统一数据格式返回的保底类 对于一些非对象的数据的再统一 即非对象的封…...

arm 平台安装snort3
本文来自原创,转载请说明来源。谢谢配合。 选择初衷 最近在学习渗透相关课程,回想起曾经拥有自己的域名和服务器的经历。不幸的是,服务器被注入了木马文件,起初并没有察觉。直到我加入了定时任务,才发现了这个问题。当时我下定决心要打造一个安全的网站,以保护自己的网…...

【Ubuntu 20.04/22.04 LTS】最新 esp-matter SDK 软件编译环境搭建步骤
仓库链接:esp-matter SDK官方软件说明:ESP Matter Programming Guide官方参考文档:使用 Matter-SDK 快速搭建 Matter 环境 (Linux) 环境要求 Ubuntu 20.04 或 Ubuntu22.04网络环境支持访问 Gihub 在安装 esp-matter SDK 软件编译环境之前&a…...

【C语言】案例:输出n位水仙花数
1.题目 输入一个整数n,输出所有n位的水仙花数 2.代码 #include <stdio.h> #include <math.h>// 计算数字的位数 int countDigits(int num) {int count 0;while (num ! 0) {num / 10;count;}return count; }// 计算水仙花数 void findNarcissisticNu…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...
