【八大排序】归并排序 | 计数排序 + 图文详解!!


文章目录
- 一、归并排序
- 1.1 基本思想 + 动图演示
- 2.2 递归版本代码实现 + 算法步骤
- 2.3 非递归版本代码实现 + 算法步骤
- 2.4 归并排序的特性总结
- 二、计数排序
- 2.1 基本思想
- 2.2 动图演示
- 2.3 算法步骤
- 2.4 代码实现
- 2.5 计数排序特性总结
- 三、排序算法复杂度及稳定性分析
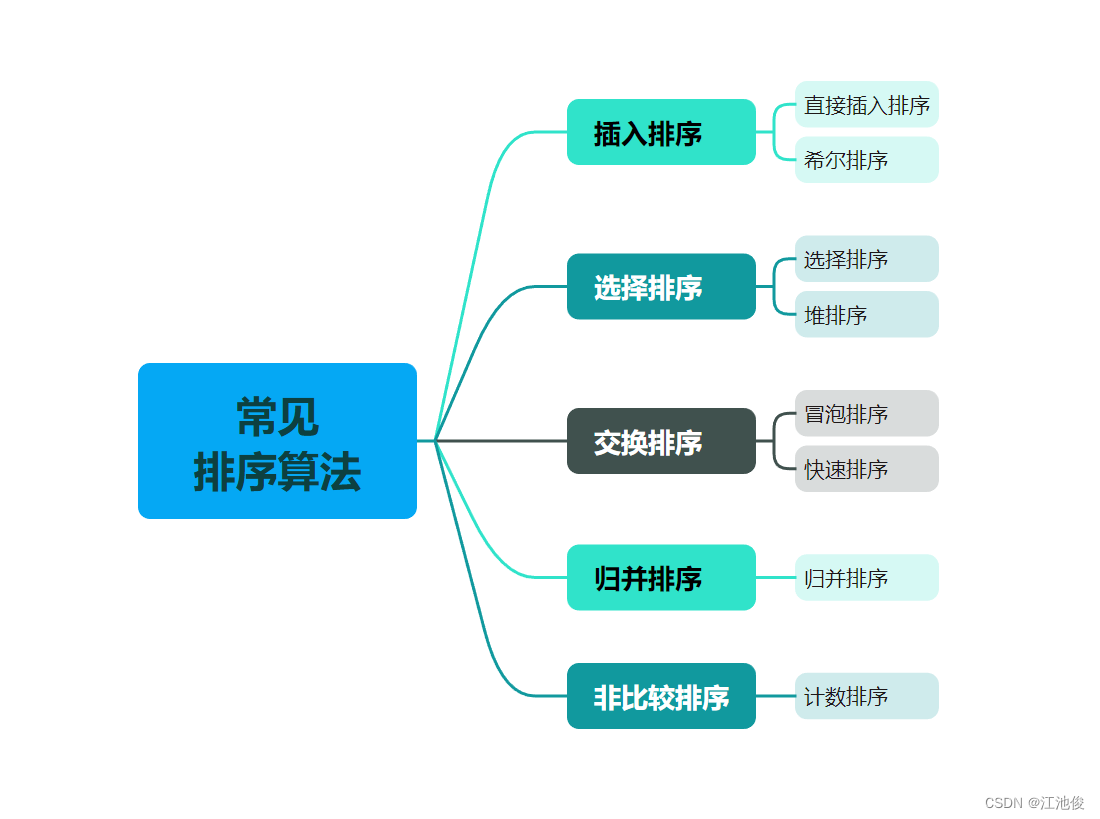
一、归并排序
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
作为一种典型的分而治之思想的算法应用,归并排序的实现由两种方法:
- 自上而下的递归(所有递归的方法都可以用迭代重写,所以就有了第 2 种方法);
- 自下而上的迭代;
1.1 基本思想 + 动图演示
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。它将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
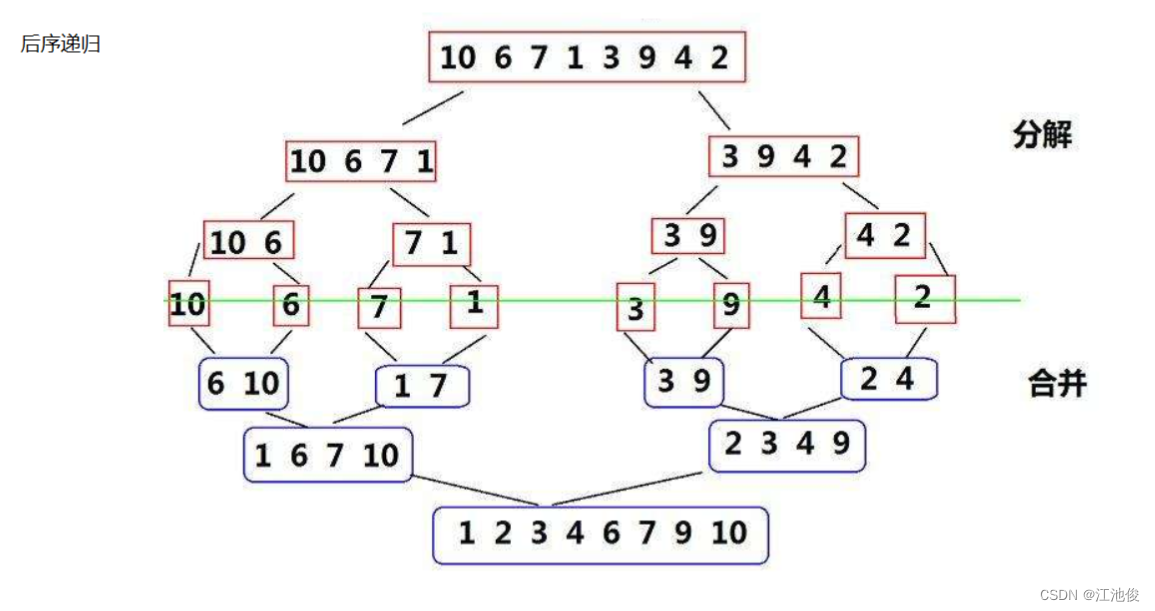
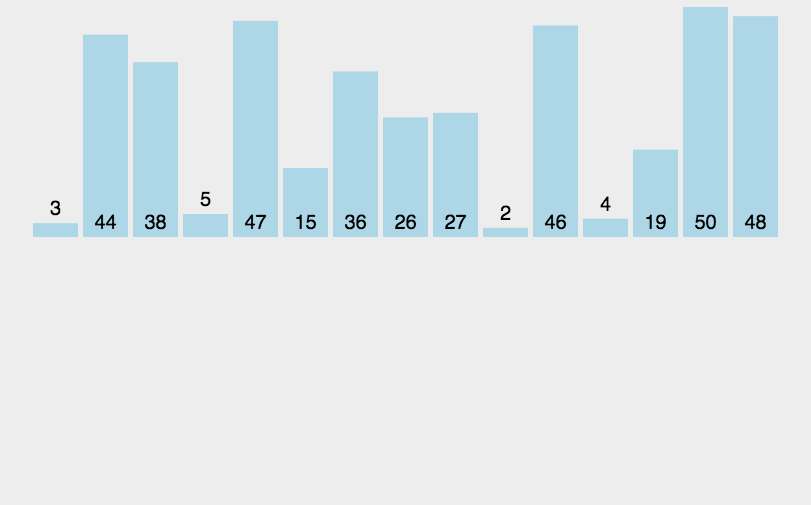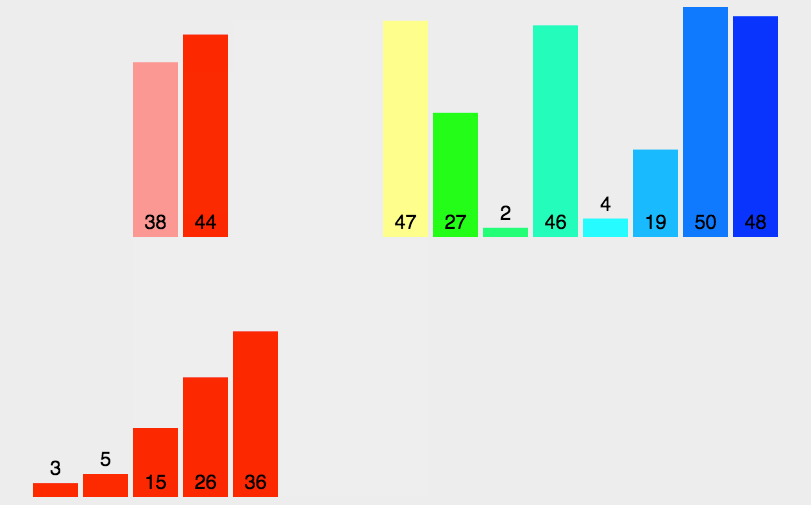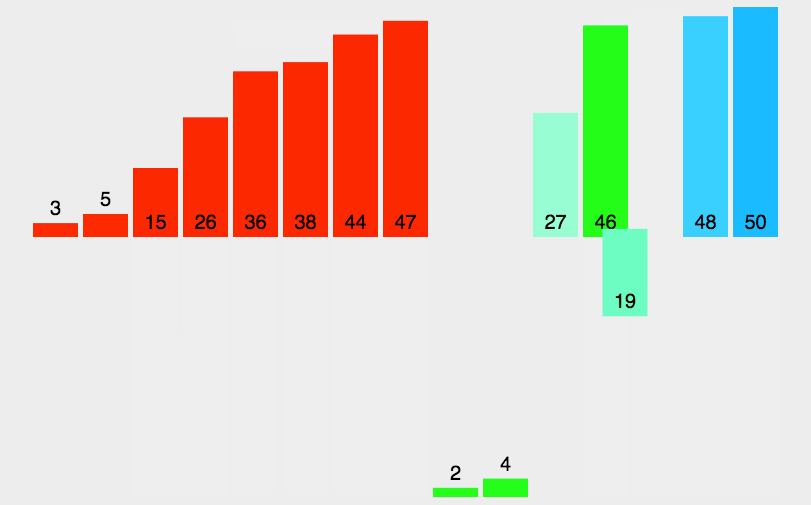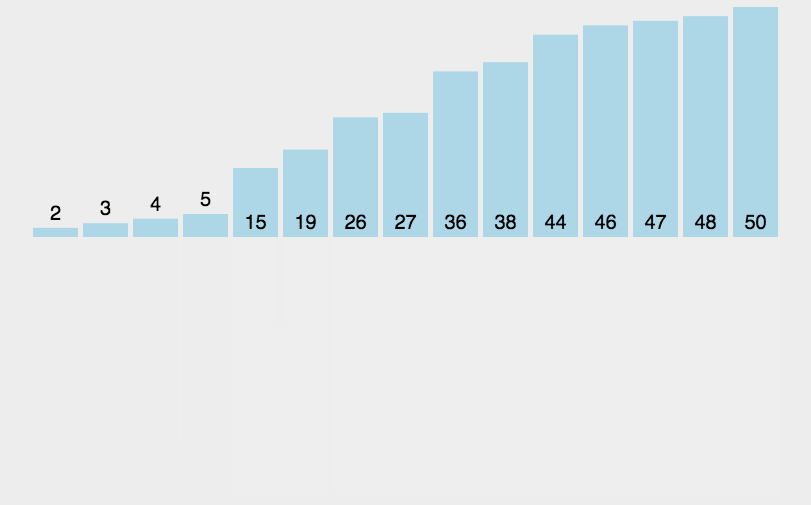
2.2 递归版本代码实现 + 算法步骤
归并排序的基本思想是分治思想,它包括以下三个步骤:
- 分解(Divide):将含有n个元素的序列分成两个各自包含大约n/2个元素的子序列。(当数组分解成一个时即可认为其有序)
- 解决(Conquer):递归地对这两个子序列进行归并排序。
- 合并(Combine):将两个排序好的子序列合并成一个最终的排序序列。
归并排序通过不断地将大问题分解成小问题来解决,即把大的数组拆分成若干个小的数组,然后逐一合并这些有序的小数组来得到最终排序好的整体数组。这种算法非常适用于链表等数据结构,在处理大规模数据时尤其高效。
// 归并排序递归函数
void _MergeSort(int* a, int begin, int end, int* temp)
{if (begin >= end)return;int mid = (begin + end) / 2;// [begin, mid] [mid+1, end]_MergeSort(a, begin, mid, temp);_MergeSort(a, mid+1, end, temp);// ... 归并 [begin,mid] [mid+1,end]int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){temp[i++] = a[begin1++];}else{temp[i++] = a[begin2++];}}while (begin1 <= end1){temp[i++] = a[begin1++];}while (begin2 <= end2){temp[i++] = a[begin2++];}// 拷贝回原数组memcpy(a + begin, temp + begin, sizeof(int) * (end - begin + 1));
}// 归并排序
void MergeSort(int* a, int n)
{// 申请一个与原数组同样大小的空间int* temp = (int*)malloc(sizeof(int) * n);if (temp == NULL){perror("malloc fail");return;}_MergeSort(a, 0, n - 1, temp);free(temp);
}
【递归展开图】:

现在我们来分析一下以上代码:
这段代码是归并排序(Merge Sort)的实现。归并排序是一种分治算法,它将一个数组分成两半,对每一半进行排序,然后将两个有序的部分合并成一个有序的数组。以下是这段代码的算法思想和步骤分析:
-
递归划分:
- 在
_MergeSort函数中,首先检查基准条件,即如果begin大于或等于end,则数组已经完全有序,所以直接返回。 - 然后,计算中间索引
mid,将数组分成两个子数组:[begin, mid]和[mid+1, end]。 - 对这两个子数组递归地进行归并排序。
- 在
-
合并:
- 在递归调用返回后,两个子数组都是有序的。然后,将这两个有序的子数组合并成一个有序的数组。
- 合并操作通过双指针技术完成。指针
begin1和begin2分别指向两个子数组的开始位置,而指针end1和end2分别指向两个子数组的结束位置。 - 开始时,从两个子数组中取最小的元素,放到临时数组
temp中,直到其中一个子数组被完全取完。 - 然后,将剩余的子数组的所有元素复制到临时数组中。
-
拷贝回原数组:
- 最后,使用
memcpy函数将临时数组中的元素复制回原数组。这一步是必要的,因为临时数组是在堆上分配的,而原数组是在栈上。
- 最后,使用
-
主函数:
MergeSort函数是归并排序的入口点。它首先在堆上为原数组分配一个同样大小的临时数组。如果分配失败(即malloc返回NULL),则输出错误信息并返回。- 然后,调用递归函数
_MergeSort对原数组进行排序。 - 最后,释放临时数组以防止内存泄漏。
-
稳定性:
- 归并排序是稳定的排序算法,这意味着相等的元素在排序后保持其原始顺序。这是因为归并排序在合并两个子数组时,总是选择较小的元素,而不改变其相对顺序。
-
时间复杂度:
- 归并排序的时间复杂度为
O(nlogn),其中n是数组的大小。这是因为每次递归调用都会将问题规模减半(logn),并且需要进行n次这样的递归调用(n)。
- 归并排序的时间复杂度为
-
空间复杂度:
- 归并排序的空间复杂度为
O(n),因为需要一个与原数组同样大小的临时数组来存储合并过程中的中间结果。
- 归并排序的空间复杂度为
2.3 非递归版本代码实现 + 算法步骤
// 归并排序(非递归)
void MergeSortNonR(int* a, int n)
{int* temp = (int*)malloc(sizeof(int) * n);if (temp == NULL){perror("malloc fail");return;}int gap = 1; // 通过gap来控制归并的两个区间的大小,表示的是这两个区间的大小while (gap < n){for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;// [begin1, end1] [begin2, end2] 归并// 边界处理if (end1 >= n || begin2 >= n){break;}if (end2 >= n){end2 = n - 1;}// 归并int j = begin1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){temp[j++] = a[begin1++];}else{temp[j++] = a[begin2++];}}while (begin1 <= end1){temp[j++] = a[begin1++];}while (begin2 <= end2){temp[j++] = a[begin2++];}// 拷贝回原数组(边归并边拷贝) --- 因为最后可能有一个区间不需要归并,所以这一个区间的元素是不需要改变的,即不需要拷贝回去,若一次性拷贝回原数组,会使这个区间的元素全部变为随机值memcpy(a + i, temp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;}free(temp);
}
对于上述代码我们接着来分析一下它的算法步骤:
【算法步骤】:
-
初始化:
- 定义一个临时数组
temp,其大小为输入数组a的大小。 - 初始化一个变量
gap为1,它表示每次归并时每组数据的个数。
- 定义一个临时数组
-
归并循环:
- 当
gap小于输入数组的长度n时,进入循环。 - 在每次循环中,将数组分为两个子数组(每个子数组的大小为
gap),并对这两个子数组进行归并。
- 当
-
子数组归并:
- 定义两个子数组的起始和结束索引:
begin1到end1和begin2到end2。 - 处理边界情况:如果其中一个子数组超出数组范围,则退出循环。
- 使用一个临时数组
temp来存储归并的结果。 - 使用一个双指针方法(类似于两个指针比较和交换)来将两个子数组合并为一个有序数组。
- 定义两个子数组的起始和结束索引:
-
拷贝回原数组:
- 使用
memcpy函数将临时数组中的数据拷贝回原数组。这一步是为了在归并过程中更新原数组。
- 使用
-
扩大gap:
- 在每次循环结束时,将
gap乘以2,以便在下一次循环中处理更大的子数组。
- 在每次循环结束时,将
-
释放内存:
- 归并完成后,释放临时数组
temp的内存。
- 归并完成后,释放临时数组
2.4 归并排序的特性总结
- 归并的缺点在于需要
O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。 - 时间复杂度:
O(N*logN) - 空间复杂度:
O(N) - 稳定性:稳定
二、计数排序
2.1 基本思想
思想:计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤:
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列中

2.2 动图演示

2.3 算法步骤
这段代码是实现计数排序算法的C语言代码。以下是该代码的算法步骤和思想分析:
算法步骤:
- 找出数组中的最小值和最大值:这是计数排序的一个重要步骤,因为算法需要对数组中的每个元素进行计数,所以需要知道元素的可能范围。
- 计算范围:根据最小值和最大值计算出元素的可能范围。
- 计数:遍历输入数组,对每个元素在其可能的范围内进行计数。
- 构建输出数组:根据计数结果,将每个元素放到它在输出数组中的正确位置。
2.4 代码实现
// 计数排序
// 时间复杂度:O(N+range) 空间复杂度:O(range)
void CountSort(int* a, int n)
{int min = a[0], max = a[0];for (int i = 1; i < n; i++){if (a[i] < min){min = a[i];}if (a[i] > max){max = a[i];}}int range = max - min + 1;int* count = (int*)calloc(range, sizeof(int));if (count == NULL){perror("calloc fail");return;}// 统计次数for (int i = 0; i < n; i++){count[a[i] - min]++;}// 排序int i = 0;for (int j = 0; j < range; j++){while (count[j]--){a[i++] = j + min;}}
}
2.5 计数排序特性总结
- 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。数排序适用于整数且范围较小的情况。对于范围较大的整数或小数,需要更复杂的排序算法。
- 时间复杂度:
O(MAX(N,范围)),由于算法只涉及到一次遍历输入数组和一次遍历计数数组,所以时间复杂度为O(MAX(N,范围))。 - 空间复杂度:
O(范围),由于需要创建一个与范围大小相等的计数数组,所以空间复杂度为O(范围)。 - 稳定性:稳定(相等的元素在排序后保持其原始顺序)
三、排序算法复杂度及稳定性分析
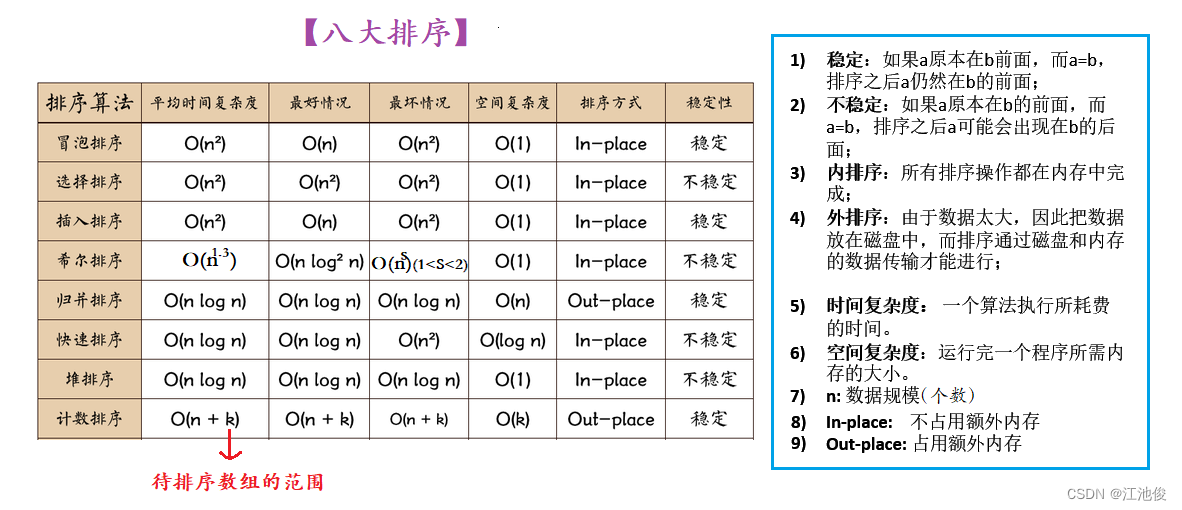
相关文章:

【八大排序】归并排序 | 计数排序 + 图文详解!!
📷 江池俊: 个人主页 🔥个人专栏: ✅数据结构冒险记 ✅C语言进阶之路 🌅 有航道的人,再渺小也不会迷途。 文章目录 一、归并排序1.1 基本思想 动图演示2.2 递归版本代码实现 算法步骤2.3 非递归版本代…...
Netty应用(三) 之 NIO开发使用 网络编程 多路复用
目录 重要:logback日志的引入以及整合步骤 5.NIO的开发使用 5.1 文件操作 5.1.1 读取文件内容 5.1.2 写入文件内容 5.1.3 文件的复制 5.2 网络编程 5.2.1 accept,read阻塞的NIO编程 5.2.2 把accept,read设置成非阻塞的NIO编程 5.2.3…...

融资项目——配置redis
一、 在maven中导入相关依赖。在springboot框架中,我们使用spring data redis <!-- spring boot redis缓存引入 --><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifa…...

npm修改镜像源
背景:切换npm镜像源是经常遇到的事,下面记录下具体操作命令 1. 打开终端运行"npm config get registry"命令来查看当前配置的镜像源 npm config get registry2. 修改成淘宝镜像源"https://registry.npmjs.org/" npm config set re…...

K8S系列文章之 [基于 Alpine 使用 kubeadm 搭建 k8s]
先部署基础环境,然后根据官方文档 K8s - Alpine Linux,进行操作。 将官方文档整理为脚本 整理脚本时,有部分调整 #!/bin/shset -x # 添加源,安装时已经配置 #cat >> /etc/apk/repositories <<"EOF" #htt…...
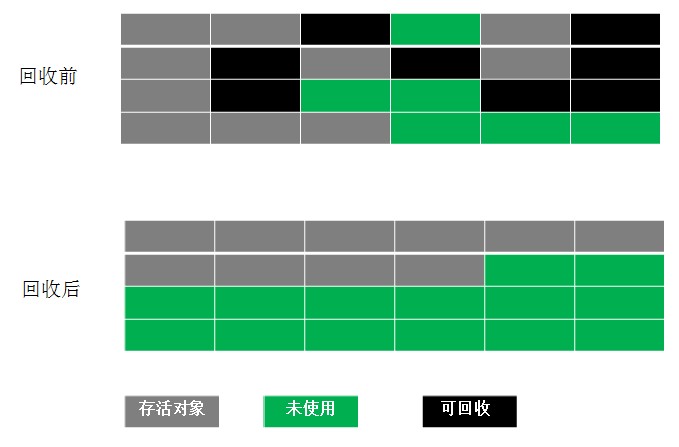
JVM相关-JVM模型、垃圾回收、JVM调优
一、JVM模型 JVM内部体型划分 JVM的内部体系结构分为三部分,分别是:类加载器(ClassLoader)子系统、运行时数据区(内存)和执行引擎 1、类加载器 概念 每个JVM都有一个类加载器子系统(class l…...

提升图像分割精度:学习UNet++算法
文章目录 一、UNet 算法简介1.1 什么是 UNet 算法1.2 UNet 的优缺点1.3 UNet 在图像分割领域的应用 二、准备工作2.1 Python 环境配置2.2 相关库的安装 三、数据处理3.1 数据的获取与预处理3.2 数据的可视化与分析 四、网络结构4.1 UNet 的网络结构4.2 UNet 各层的作用 五、训练…...
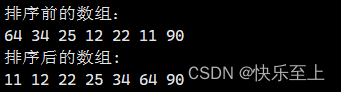
排序算法---冒泡排序
原创不易,转载请注明出处。欢迎点赞收藏~ 冒泡排序是一种简单的排序算法,其原理是重复地比较相邻的两个元素,并将顺序不正确的元素进行交换,使得每次遍历都能将一个最大(或最小)的元素放到末尾。通过多次遍…...

基于数据挖掘的微博事件分析与可视化大屏分析系统
设计原理,是指一个系统的设计由来,其将需求合理拆解成功能,抽象的描述系统的模块,以模块下的功能。功能模块化后,变成可组合、可拆解的单元,在设计时,会将所有信息分解存储在各个表中࿰…...
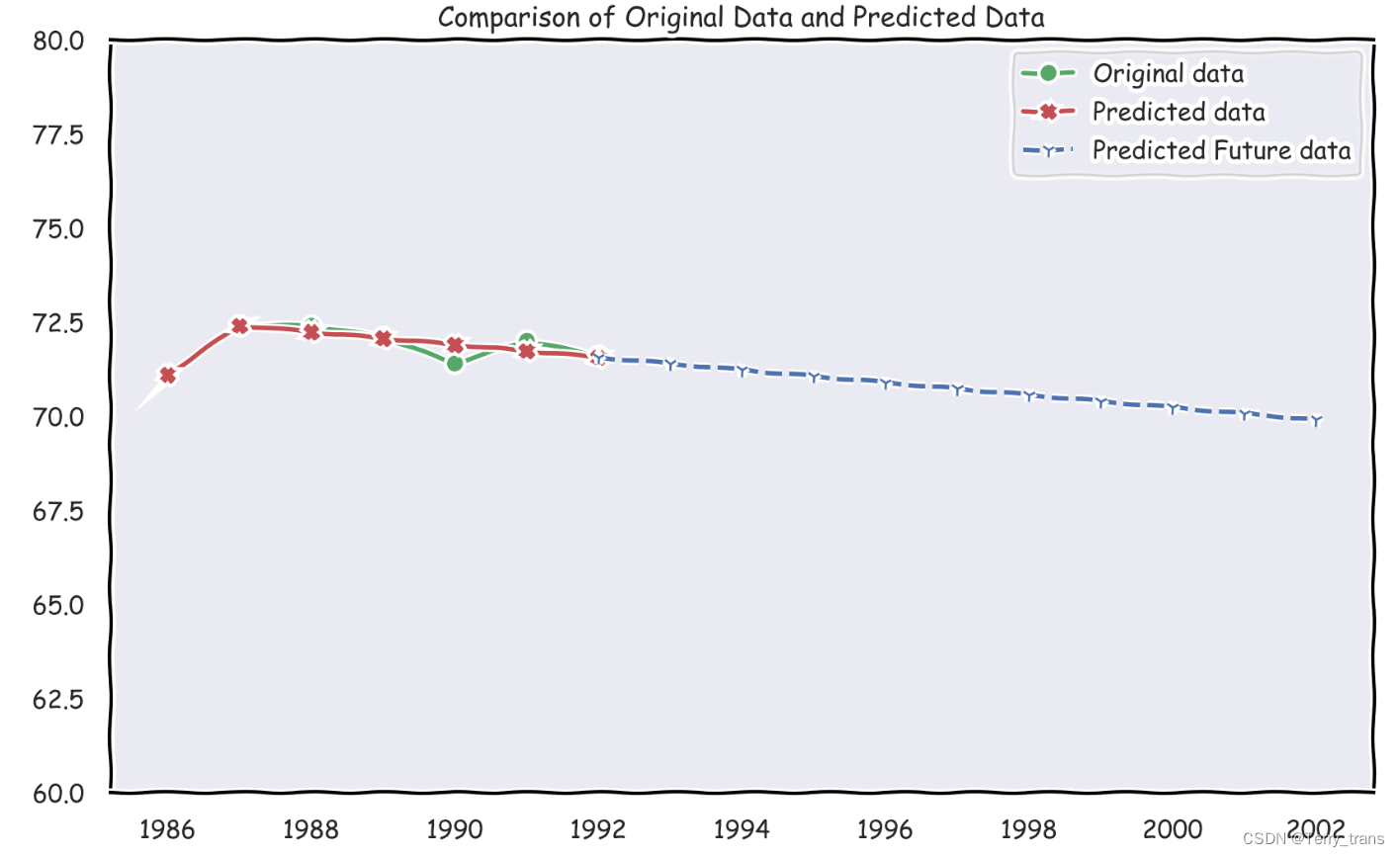
数学建模-灰色预测最强讲义 GM(1,1)原理及Python实现
目录 一、GM(1,1)模型预测原理 二、GM(1,1)模型预测步骤 2.1 数据的检验与处理 2.2 建立模型 2.3 检验预测值 三、案例 灰色预测应用场景:时间序列预测 灰色预测的主要特点是模型使用的…...
智慧自助餐饮系统(SpringBoot+MP+Vue+微信小程序+JNI+ncnn+YOLOX-Nano)
一、项目简介 本项目是配合智慧自助餐厅下的一套综合系统,该系统分为安卓端、微信小程序用户端以及后台管理系统。安卓端利用图像识别技术进行识别多种不同菜品,识别成功后安卓端显示该订单菜品以及价格并且生成进入小程序的二维码,用户扫描…...
零基础学编程从入门到精通,系统化的编程视频教程上线,中文编程开发语言工具构件之缩放控制面板构件用法
一、前言 零基础学编程从入门到精通,系统化的编程视频教程上线,中文编程开发语言工具构件之缩放控制面板构件用法 编程入门视频教程链接 https://edu.csdn.net/course/detail/39036 编程工具及实例源码文件下载可以点击最下方官网卡片——软件下载—…...
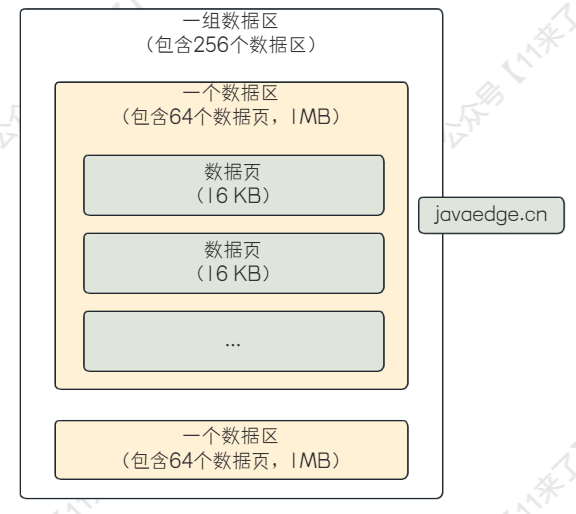
【MySQL进阶之路】MySQL 中表空间和数据区的概念以及预读机制
欢迎关注公众号(通过文章导读关注:【11来了】),及时收到 AI 前沿项目工具及新技术的推送! 在我后台回复 「资料」 可领取编程高频电子书! 在我后台回复「面试」可领取硬核面试笔记! 文章导读地址…...
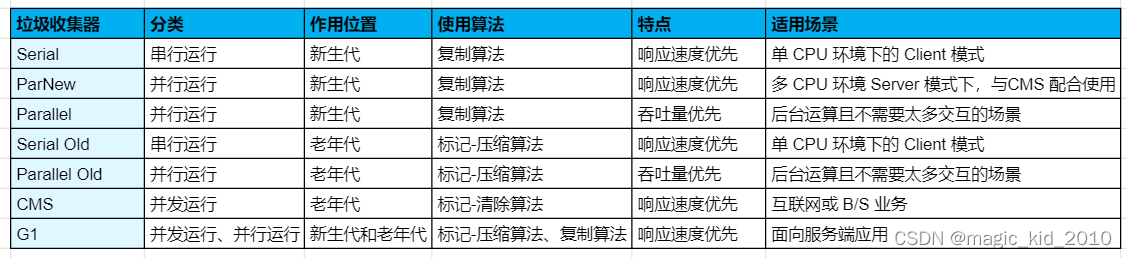
JVM 性能调优 - 常用的垃圾回收器(6)
垃圾收集器 在 JVM(Java虚拟机)中,垃圾收集器(Garbage Collector)是负责自动管理内存的组件。它的主要任务是在程序运行过程中,自动回收不再使用的对象所占用的内存空间,以便为新的对象提供足够的内存。 JVM中的垃圾收集器使用不同的算法和策略来实现垃圾收集过程,以…...

【java】Hibernate访问数据库
一、Hibernate访问数据库案例 Hibernate 是一个在 Java 社区广泛使用的对象关系映射(ORM)工具。它简化了 Java 应用程序中数据库操作的复杂性,并提供了一个框架,用于将对象模型数据映射到传统的关系型数据库。下面是一个简单的使…...
— byte数组传输)
从零开始手写mmo游戏从框架到爆炸(八)— byte数组传输
导航:从零开始手写mmo游戏从框架到爆炸(零)—— 导航-CSDN博客 Netty帧解码器 Netty中,提供了几个重要的可以直接使用的帧解码器。 LineBasedFrameDecoder 行分割帧解码器。适用场景:每个上层数据包,使…...
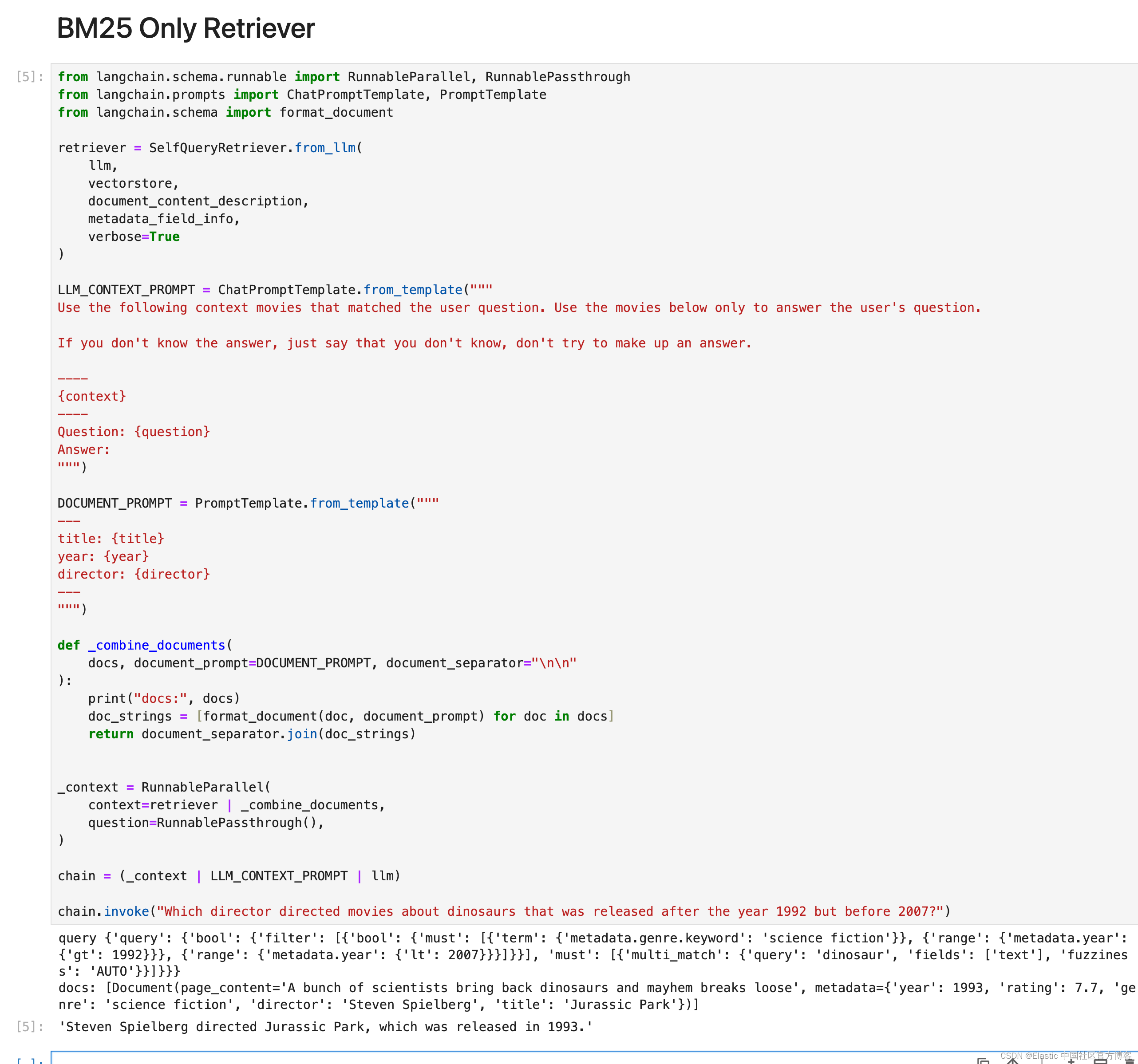
Elasticsearch:BM25 及 使用 Elasticsearch 和 LangChain 的自查询检索器
本工作簿演示了 Elasticsearch 的自查询检索器将非结构化查询转换为结构化查询的示例,我们将其用于 BM25 示例。 在这个例子中: 我们将摄取 LangChain 之外的电影样本数据集自定义 ElasticsearchStore 中的检索策略以仅使用 BM25使用自查询检索将问题转…...

uniapp的api用法大全
页面生命周期API uniApp中的页面生命周期API可以帮助开发者在页面的不同生命周期中执行相应的操作。常用的页面生命周期API包括:onLoad、onShow、onReady、onHide、onUnload等。其中,onLoad在页面加载时触发,onShow在页面显示时触发…...

笔记——asp.net core 中的 REST
REST(reprentational state transfer,表层状态转移) REST原则:提倡按照HTTP的语义使用HTTP。 如果一个系统符合REST原则,我们就说这个系统是Restful风格的。 在RPC风格的Web API系统中,我们把服务端的代码…...

排序算法---堆排序
原创不易,转载请注明出处。欢迎点赞收藏~ 堆排序(Heap Sort)是一种基于二叉堆数据结构的排序算法。它将待排序的元素构建成一个最大堆(或最小堆),然后逐步将堆顶元素与堆的最后一个元素交换位置,…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
