1184. 欧拉回路(欧拉回路,模板题)
活动 - AcWing
给定一张图,请你找出欧拉回路,即在图中找一个环使得每条边都在环上出现恰好一次。
输入格式
第一行包含一个整数 t,t∈{1,2},如果 t=1,表示所给图为无向图,如果 t=2,表示所给图为有向图。
第二行包含两个整数 n,m,表示图的结点数和边数。
接下来 m 行中,第 i 行两个整数 vi,ui,表示第 i 条边(从 11 开始编号)。
- 如果 t=1 则表示 vi 到 ui 有一条无向边。
- 如果 t=2 则表示 vi 到 ui 有一条有向边。
图中可能有重边也可能有自环。
点的编号从 1 到 n。
输出格式
如果无法一笔画出欧拉回路,则输出一行:NO。
否则,输出一行:YES,接下来一行输出 任意一组 合法方案即可。
- 如果 t=1,输出 m 个整数 p1,p2,…,pm。令 e=|pi|,那么 e 表示经过的第 i 条边的编号。如果 pi 为正数表示从 ve 走到 ue,否则表示从 ue 走到 ve。
- 如果 t=2,输出 m 个整数 p1,p2,…,pm。其中 pi 表示经过的第 i 条边的编号。
数据范围
1≤n≤105
0≤m≤2×105
输入样例1:
1
3 3
1 2
2 3
1 3
输出样例1:
YES
1 2 -3
输入样例2:
2
5 6
2 3
2 5
3 4
1 2
4 2
5 1
输出样例2:
YES
4 1 3 5 2 6解析:
一、在无向图中(所有边都是连通的):
(1)存在欧拉路径的充分必要条件:度数为奇数的点只能有0或2。
(2)存在欧拉回路(起点和终点相同)的充分必要条件:度数为奇数的点只能有0个。
二、在有向图中(所有边都是连通的):
(1)存在欧拉路径的充分必要条件:要么所有点的入度均等于入度;要么除了两个点之外,其余所有的点的出度等于入度,剩余的两个点:一个满足出度比入度多1(起点),另一个满足入度比出度多1(终点)。
(2)存在欧拉回路(起点和终点相同)的充分必要条件:所有点的入度均等于出度。
欧拉回路的dfs用边来判重,不能用点。
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
#include<unordered_set>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
const int N = 1e5 + 5, M = 4e5 + 5, INF = 0x3f3f3f3f;int n, m;
int h[N], e[M], ne[M], idx;
int din[N], dout[N];
int ans[M], cnt;
bool used[M];
int type;void add(int a, int b) {e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}void dfs(int u) {//cout << "_______________________" << u << endl;for (int& i = h[u]; i != -1;) {if (used[i]) {i = ne[i];continue;}int t;if (type == 1) {t = i / 2 + 1;if (i & 1)t = -t;}else t = i + 1;used[i] = 1;if (type == 1) {used[i ^ 1] = 1;}int j = e[i];i = ne[i];dfs(j);ans[++cnt] = t;}
}int main() {cin >> type;cin >> n >> m;memset(h, -1, sizeof h);for (int i = 1,a,b; i <= m; i++) {scanf("%d%d", &a, &b);add(a, b);if (type == 1)add(b, a);din[b]++, dout[a]++;}if (type == 1) {for (int i = 1; i <= n; i++) {if (din[i] + dout[i] & 1) {cout << "NO" << endl;return 0;}}}else {for (int i = 1; i <= n; i++) {if (din[i] != dout[i]) {cout << "NO" << endl;return 0;}}}for (int i = 1; i <= n; i++) {if (h[i] != -1) {dfs(i);break;}}if (cnt < m) {cout << "NO" << endl;return 0;}cout << "YES" << endl;for (int i = cnt; i; i--) {printf("%d ", ans[i]);}return 0;
}相关文章:
)
1184. 欧拉回路(欧拉回路,模板题)
活动 - AcWing 给定一张图,请你找出欧拉回路,即在图中找一个环使得每条边都在环上出现恰好一次。 输入格式 第一行包含一个整数 t,t∈{1,2},如果 t1,表示所给图为无向图,如果 t2,表示所给图为…...

学习 Redis 基础数据结构,不讲虚的。
学习 Redis 基础数据结构,不讲虚的。 一个群友给我发消息,“该学的都学了,怎么就找不到心意的工作,太难了”。 很多在近期找过工作的同学一定都知道了,背诵八股文已经不是找工作的绝对王牌。企业最终要的是可以创造价…...

Android 11 webview webrtc无法使用问题
问题:Android 11 webview 调用webrtc无法使用, 看logcat日志会报如下错误 [ERROR:address_tracker_linux.cc(245)] Could not send NETLINK request: Permission denied (13) 查了下相关的网络权限都有配置了还是不行,还是报这个权限问题 原因࿱…...
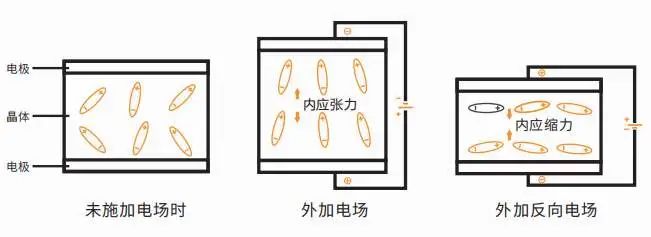
嵌入式单片机中晶振的工作原理
晶振在单片机中是必不可少的元器件,只要用到CPU的地方就必定有晶振的存在,那么晶振是如何工作的呢? 什么是晶振 晶振一般指晶体振荡器,晶体振荡器是指从一块石英晶体上按一定方位角切下的薄片,简称为晶片。 石英晶体谐…...
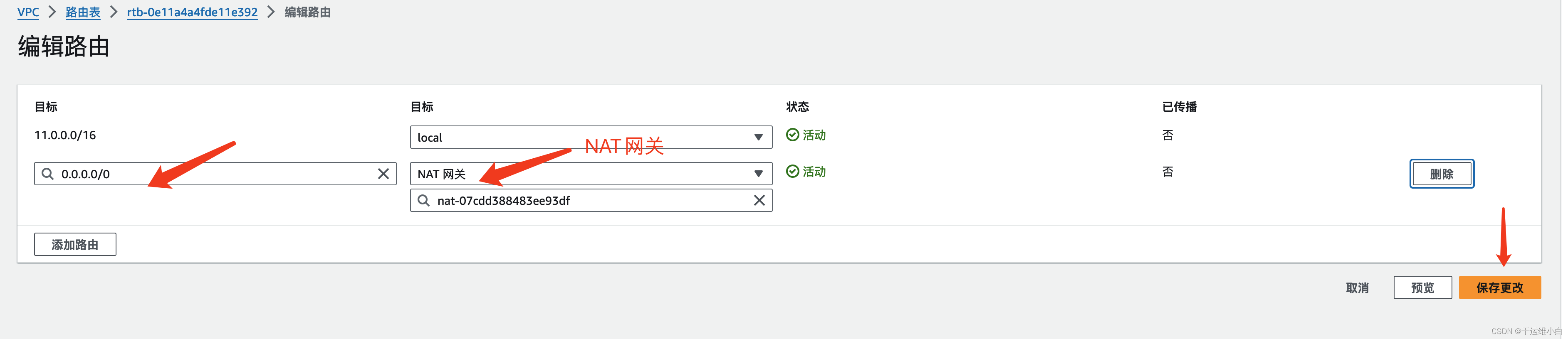
AWS配置内网EC2服务器上网【图形化配置】
第一种方法:创建EC2选择启用分配公网ip 1. 创建vpc 2. 创建子网 3. 创建互联网网关 创建互联网网关 创建互联网网关 ,设置名称即可 然后给网关附加到新建的vpc即可 4. 给新建子网添加路由规则,添加新建的互联网网关然后点击保存更改 5. 新建…...
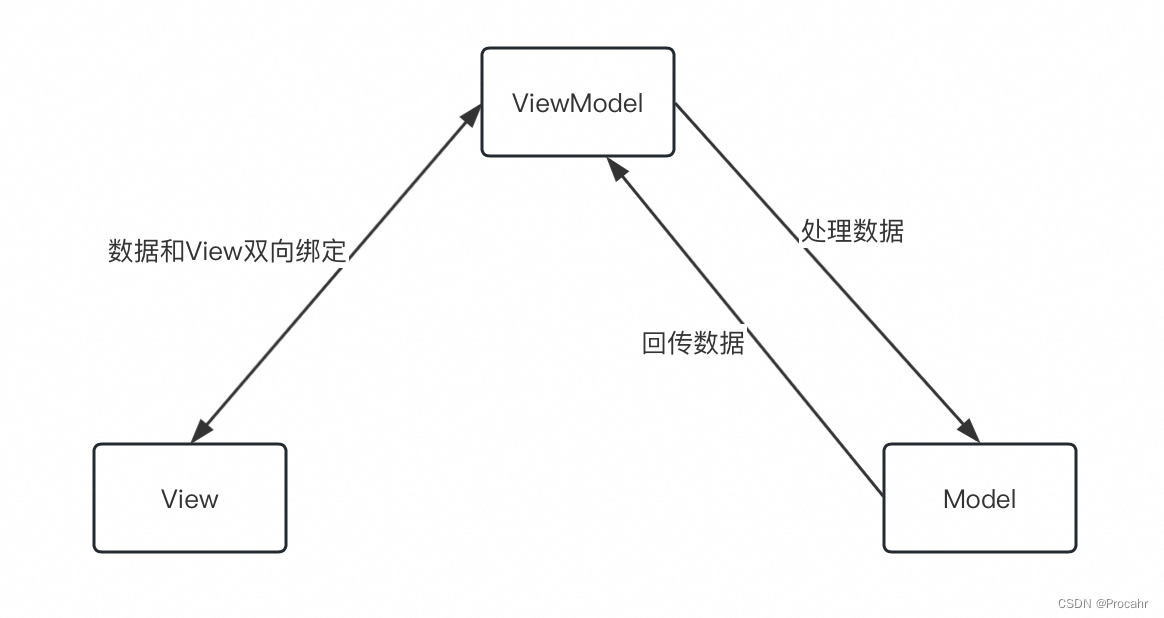
Android中的MVVM
演变 开发常用的框架包括MVC、MVP和本文的MVVM,三种框架都是为了分离ui界面和处理逻辑而出现的框架模式。mvp、mvvm都由mvc演化而来,他们不属于某种语言的框架,当存在ui页面和逻辑代码时,我们就可以使用这三种模式。 model和vie…...

制作耳机壳的UV树脂和塑料材质相比劣势有哪些?
以下是UV树脂相比塑料材质可能存在的劣势: 价格较高:相比一些常见的塑料材质,UV树脂的价格可能较高。这主要是因为UV树脂的生产过程较为复杂,需要较高的技术和设备支持。加工难度大:虽然UV树脂的加工过程相对简单&…...

CSP-202012-1-期末预测之安全指数
CSP-202012-1-期末预测之安全指数 题目很简单,直接上代码 #include <iostream> using namespace std; int main() {int n, sum 0;cin >> n;for (int i 0; i < n; i){int w, score;cin >> w >> score;sum w * score;}if (sum > 0…...

Doris中的本地routineload环境,用于开发回归测试用例
----------------2024-2-6-更新-------------- doris的routineload,就是从kafka中加载数据到表,特点是定时、周期性的从kafka取数据。 要想在本地开发测试routine load相关功能,需要配置kafka环境,尤其是需要增加routine load回…...
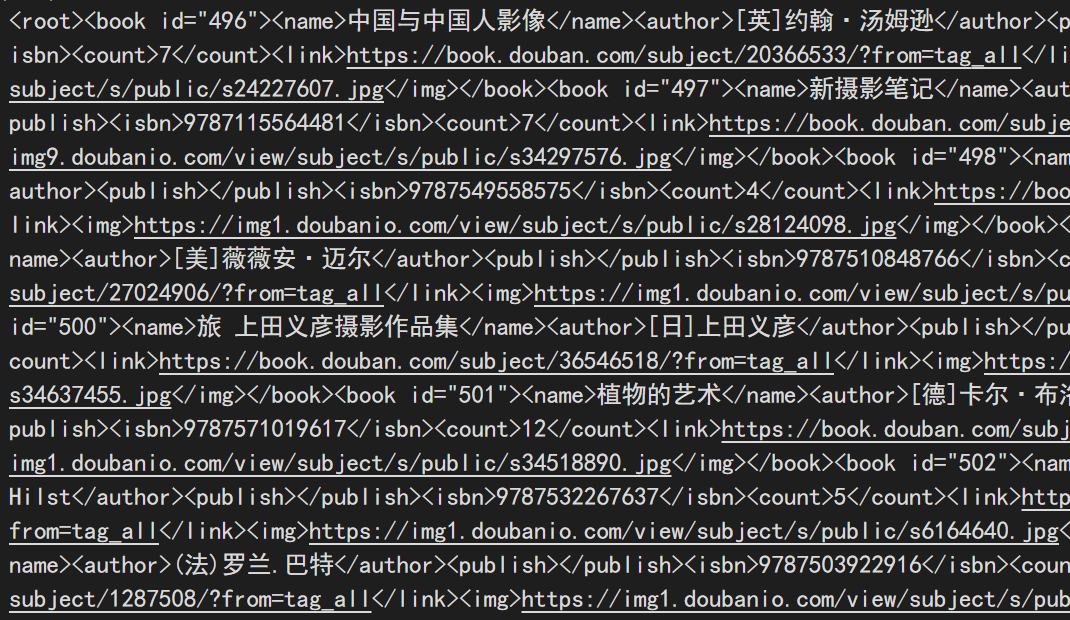
【开源项目阅读】Java爬虫抓取豆瓣图书信息
原项目链接 Java爬虫抓取豆瓣图书信息 本地运行 运行过程 另建项目,把四个源代码文件拷贝到自己的包下面 在代码爆红处按ALTENTER自动导入maven依赖 直接运行Main.main方法,启动项目 运行结果 在本地磁盘上生成三个xml文件 其中的内容即位爬取…...
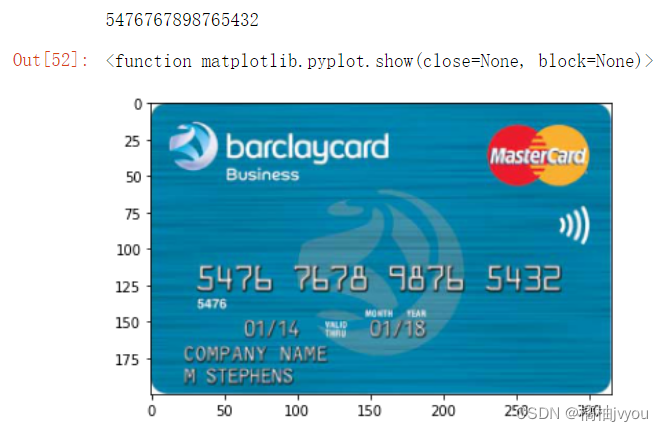
基于opencv-python模板匹配的银行卡号识别(附源码)
目录 介绍 数字模板处理 银行卡图片处理 导入数字模板 模板匹配及结果 介绍 我们有若干个银行卡图片和一个数字模板图片,如下图 我们的目的就是通过对银行卡图片进行一系列图像操作使得我们可以用这个数字模板检测出银行卡号。 数字模板处理 首先我们先对数…...
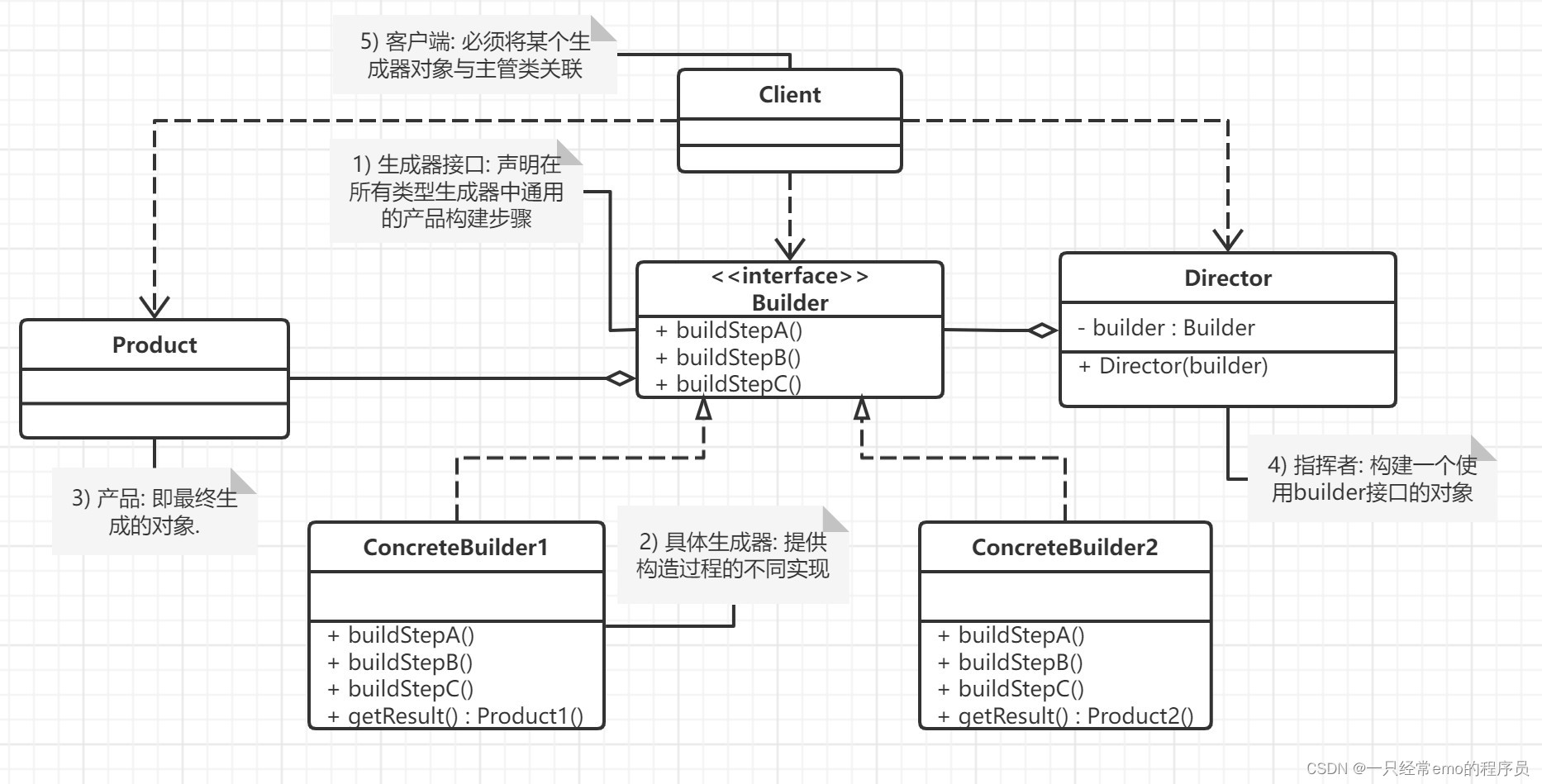
JAVA设计模式之建造者模式详解
建造者模式 1 建造者模式介绍 建造者模式 (builder pattern), 也被称为生成器模式 , 是一种创建型设计模式. 定义: 将一个复杂对象的构建与表示分离,使得同样的构建过程可以创建不同的表示。 **建造者模式要解决的问题 ** 建造者模式可以将部件和其组装过程分开…...
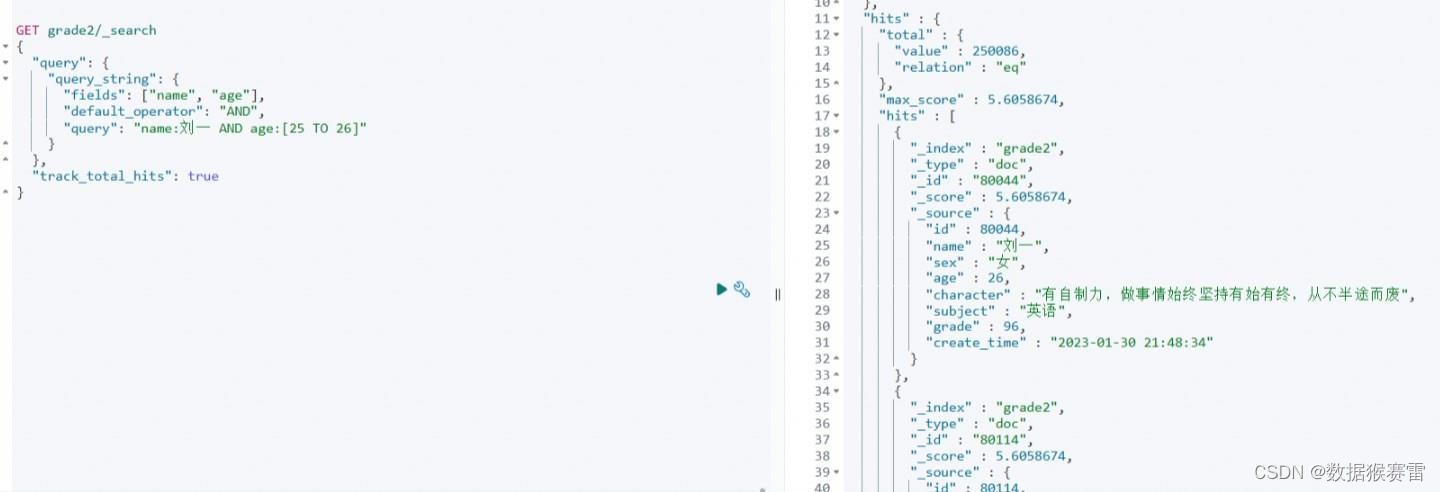
ElasticSearch查询语句用法
查询用法包括:match、match_phrase、multi_match、query_string、term 1.match 1.1 不同字段权重 如果需要为不同字段设置不同权重,可以考虑使用bool查询的should子句来组合多个match查询,并为每个match查询设置不同的权重 {"query&…...

美国服务器如何
美国服务器在被选择名单里排名很高,那么美国服务器如何,美国服务器 适用于哪些场景,认可度高吗?接下来小编为您整理发布美国服务器如何的详细情况。 美国服务器通常以其高性能、高可靠性和安全性而受到认可,它们适用于多种业务场…...

远程主机可能不符合glibc和libstdc++ VS Code服务器的先决条件
报错信息 VSCode无法连接远程服务器,终端一直提醒: [22:46:01.906] > Waiting for server log... [22:46:01.936] > Waiting for server log... [22:46:01.951] > [22:46:01.967] > Waiting for server log... [22:46:01.982] > [22:…...

【python基础】sys.argv[]的使用方法
文章目录 前言一、sys.argv是什么?二、实例 前言 本文主要讲解sys.argv[]的使用方法。 一、sys.argv是什么? sys.arg[]的作用就是存储在运行python脚本时候从外部往被运行的py文件里面传递的参数,是一个列表对象。利用好这个属性可以极大的增…...

Element-Ui el-date-picker日期传值异常问题解决办法
首先,只要非常简单的组件引入写法: 然后myDate在data()中是字符串类型 myDate: ‘’ 然后增加一个方法在提交表单到后台的时候,用来转化日期对应到myDate成字符串类型,并且对应到java类 function checkType(value) {if (typeo…...
GO语言集成开发 JetBrains GoLand 2023 中文
JetBrains GoLand 2023是一款专为Go语言开发者打造的集成开发环境(IDE)。它基于IntelliJ IDEA平台,提供了丰富的功能和工具,旨在提高开发效率和质量。GoLand 2023具备强大的Go语言支持,包括语法高亮、自动补全、代码提…...

详细关于如何解决mfc140.dll丢失的步骤,有效修复mfc140.dll文件丢失的问题。
mfc140.dll文件是Microsoft Visual Studio 2015程序集之一,它包含用于支持多种功能的代码和库。当这个mfc140.dll文件丢失时,可能会导致相关程序运行出错甚至无法运行。很多用户可能会遇到mfc140.dll丢失的问题,但是这并不是不可解决的困难。…...

聚簇索引、非聚簇索引、回表、索引下推、覆盖索引
聚簇索引(主键索引) 非叶子节点上存储的是索引值,叶子节点上存储的是整行记录。 非聚簇索引(非主键索引、二级索引) 非叶子节点上存储的都是索引值,叶子节点上存储的是主键的值。非聚簇索引需要回表&…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...
