Element-Ui el-date-picker日期传值异常问题解决办法
首先,只要非常简单的组件引入写法:
然后myDate在data()中是字符串类型
myDate: ‘’
然后增加一个方法在提交表单到后台的时候,用来转化日期对应到myDate成字符串类型,并且对应到java类
function checkType(value) {if (typeof value === 'string') {console.log('This value is a string.');} else if (value instanceof Date) {console.log('This value is a Date.');} else {console.log('This value is neither a string nor a Date.');}
}let dateString = '2023-10-11';
let dateObject = new Date('2023-10-11');
注意点选的日期会是Date()类型
let date = new Date();
let dateString = `${date.getFullYear()}-${(date.getMonth() + 1).toString
().padStart(2, '0')}-${date.getDate().toString().padStart(2, '0')}`;
console.log(dateString); // Outputs: "2023-10-11"
以上代码汇总:
<el-date-picker v-model="myDate"></el-date-picker>myDate: ''function checkType(value) {if (typeof value === 'string') {return value.replace(/\//g, "-")} else if (value instanceof Date) {let dateString = `${date.getFullYear()}-${(date.getMonth() + 1).toString
().padStart(2, '0')}-${date.getDate().toString().padStart(2, '0')}`
return dateString} else {console.log('This value is neither a string nor a Date.');}
}formDate.completeDate = dateStringjava对应参数类
@JsonFormat(pattern="yyyy-MM-dd", timezone="Asia/Shanghai")
private Date completeDate;注意特殊情况:
v-model中不要连续嵌套多个变量比如:
如果有多个变量嵌套的情况,则v-model先绑定到一个中介变量,然后通过watch中介变量,转换格式后,再对
a.b.c.myDate赋值。
另外,直接选择日期的时候,一般其实个Date对象,但是很多人会将myDate直接声明为’',所以才会出现可能不能点选的问题,所以才会引入以上需要转化之类的操作。
相关文章:

Element-Ui el-date-picker日期传值异常问题解决办法
首先,只要非常简单的组件引入写法: 然后myDate在data()中是字符串类型 myDate: ‘’ 然后增加一个方法在提交表单到后台的时候,用来转化日期对应到myDate成字符串类型,并且对应到java类 function checkType(value) {if (typeo…...
GO语言集成开发 JetBrains GoLand 2023 中文
JetBrains GoLand 2023是一款专为Go语言开发者打造的集成开发环境(IDE)。它基于IntelliJ IDEA平台,提供了丰富的功能和工具,旨在提高开发效率和质量。GoLand 2023具备强大的Go语言支持,包括语法高亮、自动补全、代码提…...

详细关于如何解决mfc140.dll丢失的步骤,有效修复mfc140.dll文件丢失的问题。
mfc140.dll文件是Microsoft Visual Studio 2015程序集之一,它包含用于支持多种功能的代码和库。当这个mfc140.dll文件丢失时,可能会导致相关程序运行出错甚至无法运行。很多用户可能会遇到mfc140.dll丢失的问题,但是这并不是不可解决的困难。…...

聚簇索引、非聚簇索引、回表、索引下推、覆盖索引
聚簇索引(主键索引) 非叶子节点上存储的是索引值,叶子节点上存储的是整行记录。 非聚簇索引(非主键索引、二级索引) 非叶子节点上存储的都是索引值,叶子节点上存储的是主键的值。非聚簇索引需要回表&…...
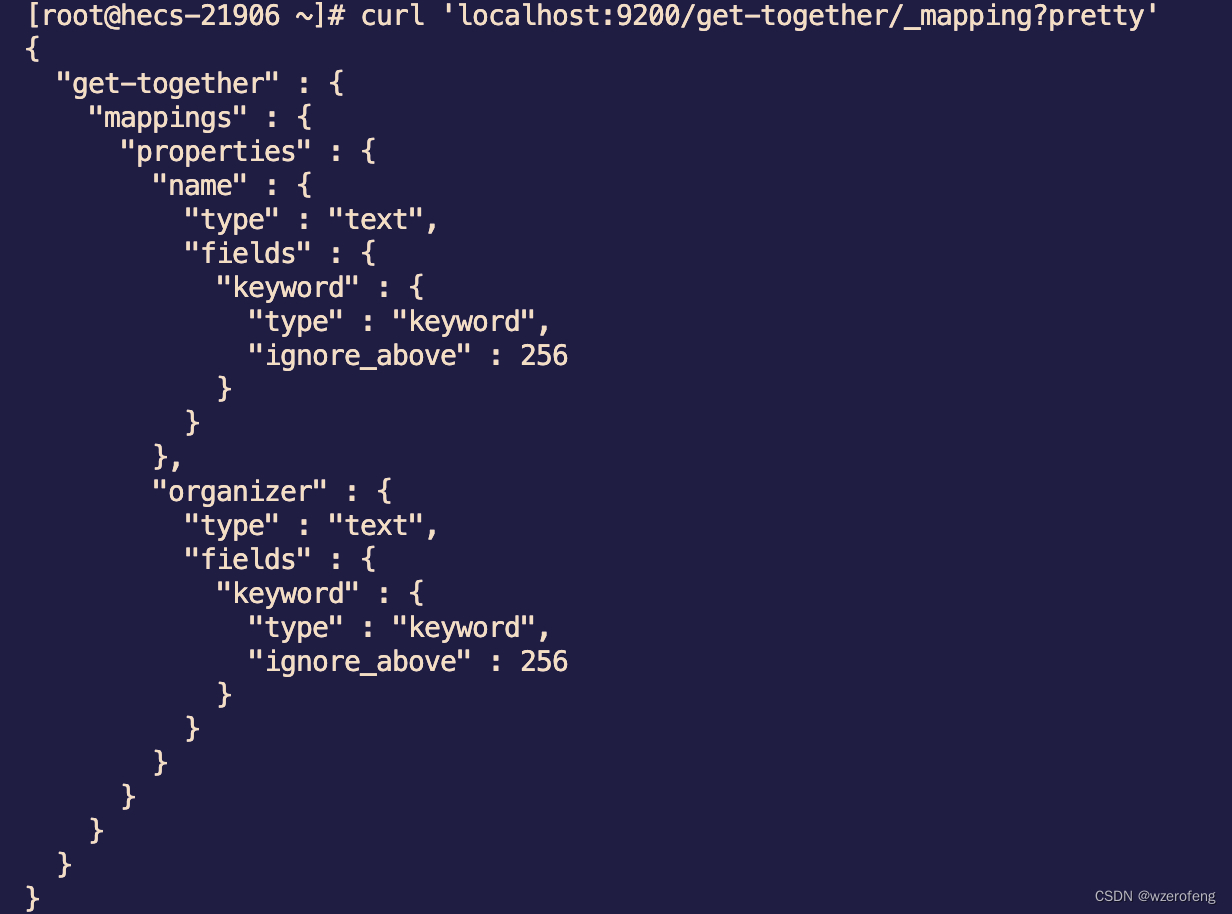
ES实战-book笔记1
#索引一个文档,-XPUT手动创建索引, curl -XPUT localhost:9200/get-together/_doc/1?pretty -H Content-Type: application/json -d {"name": "Elasticsearch Denver","organizer": "Lee" } #返回结果 {"_index" : "g…...

高防服务器出租的优势及特点
高防服务器出租是指租用具备高防御能力的服务器,用于应对网络攻击、保护网站和数据安全。那么为什么会选择高防服务器出租,小编为您整理发布高防服务器出租的优势及特点。 高防服务器通常具备以下特点: 1. 高性能硬件配置:高防服务…...

NTLM||LM算法lsasswinlogon进程
来填坑了,这篇blog我们就来讲一下mimikatz能抓到开机的密码的原理 1.lsass&&winlogon 不知道大家有没有好奇过,我们每次开机输入密码之后,电脑又怎么知道我们是否输入正确呢? :这就要的得益于我们的两个进程…...
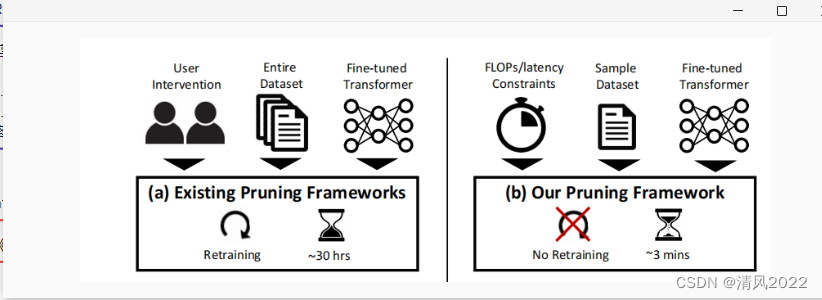
transformer剪枝论文汇总
文章目录 NN Pruning摘要实验 大模型剪枝LLM-PrunerSparseGPT LTPVTPWidth & Depth PruningPatch SlimmingDynamicViTSPViTDynamicBERTViT SlimmingFastFormersNViTUVCPost-training pruning NN Pruning 《Block Pruning For Faster Transformers》 《为更快的transformer…...
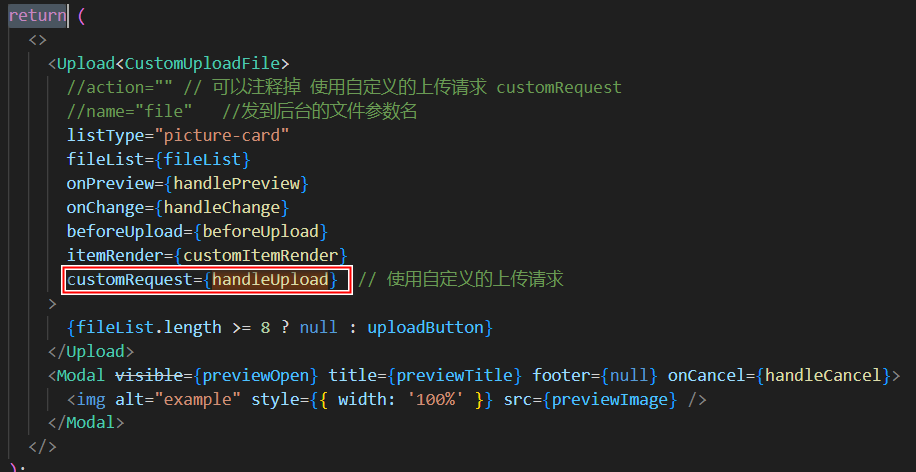
使用 Ant Design 的 Upload 组件实现图片
文章目录 使用 Ant Design 的 Upload 组件实现图片Upload组件itemRender自定义上传列表项的渲染方式修改图片名上传图片上传链接中添加 Bearer Token 的请求头onPreview{handlePreview}上传成功后,如何隐藏上传列表 使用 Ant Design 的 Upload 组件实现图片 Upload…...

【知识图谱--第二讲知识图谱的表示】
知识图谱的表示 知识表示Knowledge Representation 知识表示方法知识图谱的符号表示基于图的知识表示与建模简单图建模-最简单的无向图有向标记图OWL与Ontology 知识图谱的向量表示 知识表示 Knowledge Representation 知识表示(KR)就是用易于计算机处…...

C语言---计算n的阶乘
阶乘的概念:一个正整数的阶乘(factorial)是所有小于及等于该数的正整数的积,且0的阶乘为1,自然数n的阶乘写作n! 。 任何大于等于1 的自然数n 阶乘表示方法: n!123…(n-1)n 或 n!n(n-1)! 0!1 …...

材料非线性Matlab有限元编程:初应力法与初应变法
导读:本文主要围绕材料非线性问题的有限元Matlab编程求解进行介绍,重点围绕牛顿-拉普森法(切线刚度法)、初应力法、初应变法等三种非线性迭代方法的算法原理展开讲解,最后利用Matlab对材料非线性问题有限元迭代求解算法进行实现,展示了实现求解的核心代码。这些内容都将收…...
)
QT+OSG/osgEarth编译之八十二:osgdb_obj+Qt编译(一套代码、一套框架,跨平台编译,版本:OSG-3.6.5插件库osgdb_obj)
文章目录 一、osgdb_obj介绍二、文件分析三、pro文件四、编译实践一、osgdb_obj介绍 OBJ格式是一种标准的3D模型文件格式,它以纯文本形式存储关于3D模型的信息。这种格式最初由Wavefront Technologies为其高级可视化系统开发,后来被广泛应用于3D软件之间的数据交换。OBJ格式…...
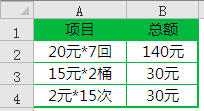
[office] excel求乘积的公式和方法 #媒体#笔记#经验分享
excel求乘积的公式和方法 本文首先给出两个常规的excel求乘积的链接,然后再例举了一个文字和数字在同一单元格里面的excel求乘积的公式写法。 excel求乘积的方法分为两种,第一种是直接用四则运算的*来求乘积,另外一种就是使用PRODUCT乘积函数…...
OpenEuler20.03LTS SP2 上安装 OpenGauss3.0.0 单机部署过程(二)
开始安装 OpenGauss 数据库 3.1.7 安装依赖包 (说明:如果可以联网,可以通过网络 yum 安装所需依赖包,既可以跳过本步骤。如果网络无法连通,请把本文档所在目录下的依赖包上传到服务器上,手工安装后,即无需通过网络进行 Yum 安装了): 上传:libaio-0.3.111-5.oe1.x8…...

从零开始手写mmo游戏从框架到爆炸(十)— 集成springboot-jpa与用户表
导航:从零开始手写mmo游戏从框架到爆炸(零)—— 导航-CSDN博客 集成springboot-jpa,不用mybatis框架一个是方便对接不同的数据源。第二个目前规划的游戏内容可能对数据库的依赖不是很大,jpa应该肯定能满足要求了…...

Python算法题集_两两交换链表中的节点
Python算法题集_两两交换链表中的节点 题24:两两交换链表中的节点1. 示例说明2. 题目解析- 题意分解- 优化思路- 测量工具 3. 代码展开1) 标准求解【四节点法】2) 改进版一【列表操作】3) 改进版二【三指针法】4) 改进版三【递归大法】 4. 最优算法 本文为Python算法…...

米贸搜|Facebook在购物季使用的Meta广告投放流程
一、账户简化 当广告系列开始投放后,每个广告组都会经历一个初始的“机器学习阶段”。简化账户架构可以帮助AI系统更快获得广告主所需的成效。例如: 每周转化次数超过50次的广告组,其单次购物费用要低28%;成功结束机器学习阶段的…...

前端滚动组件分享
分享一个前端可视化常用的卡片列表滚动组件,常用于可视化项目左右两侧的卡片列表的滚动。效果如下图所示: 组件描述 当鼠标移入滚动区域时,滚动行为停止当鼠标再次离开时,滚动继续 源码展示 <template><div ref"…...
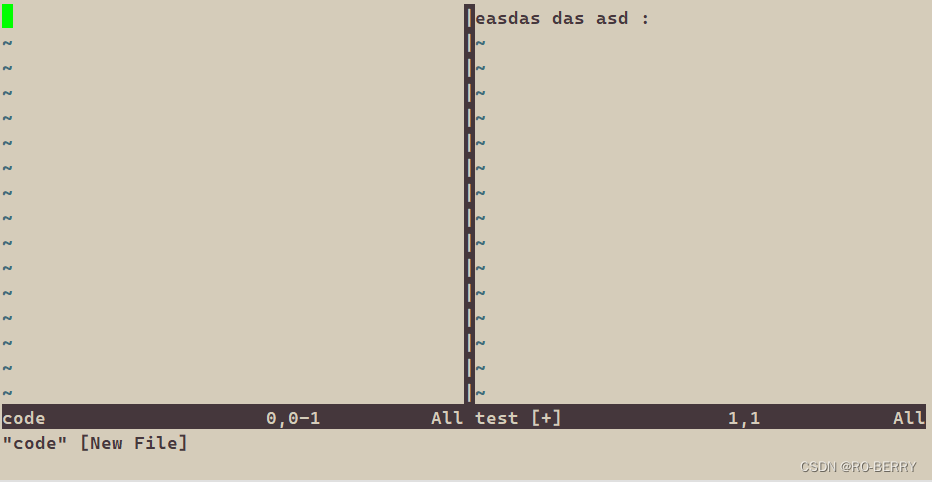
【linux开发工具】vim详解
📙 作者简介 :RO-BERRY 📗 学习方向:致力于C、C、数据结构、TCP/IP、数据库等等一系列知识 📒 日后方向 : 偏向于CPP开发以及大数据方向,欢迎各位关注,谢谢各位的支持 “学如逆水行舟࿰…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...
