材料非线性Matlab有限元编程:初应力法与初应变法
导读:本文主要围绕材料非线性问题的有限元Matlab编程求解进行介绍,重点围绕牛顿-拉普森法(切线刚度法)、初应力法、初应变法等三种非线性迭代方法的算法原理展开讲解,最后利用Matlab对材料非线性问题有限元迭代求解算法进行实现,展示了实现求解的核心代码。这些内容都将收录在我的原创精品课《matlab有限元编程从入门到精通》。
一、 切线刚度法
大家可以查阅我上月发布在仿真秀的原创文章《材料非线性Matlab有限元编程:切线刚度法》
二、初应力及初应变法
1、本构方程
本文同样以具体案例为对象进行材料非线性问题的有限元变成求解,求解模型如图1,模型边界为20m×10m,公式1-3材料本构方程如公式1所示,其中,弹性模量E=20MPa,泊松比0.35,模型上表面中间位置作用20kPa超载,超载作用范围为4m。按照平面应变问题考虑,使用常应变三角形单元分析模型上表面中间点竖向沉降,对应的有限元模型和计算结果如图2、3所示。
之所以采用公式1-3三种不同的应力应变关系本构方程,是因为牛顿-拉普森法(切线刚度法)、初应力法、初应变法适用于不同形式的本构方程:切线刚度法,顾名思义,其刚度表达式为应力应变曲线的切线,因此采用微分形式表示其本构关系;初应力法适用于应力由应变确定的本构形式,即应力为应变量,应变为自变量;但某些问题中,应力无法用应变显式表达,相反,应变由应力表达的本构形式,这种情况的非线性本构方程采用初应变法来求解,


图1 材料非线性问题案例模型
2、有限元求解原理
由图2所示,有限元离散方式采用的是三节点三角形单元进行离散,因此我们要有三角形平面单元弹性问题的求解基础知识,大家可以观看b站的《Matlab有限元编程从入门到精通》课程中的“三角形单元悬臂梁matlab有限元编程”小节,详细讲解了基于三角形三节点单元的有限元离散过程以及弹性刚度矩阵的推导。

图2 三节点三角形单元刚度矩阵推导
但需要注意的是,该平面三角形单元应用的场景是平面应力问题,本案例是平面应变问题,二者的区别如下图所示,除物理方程外,平面应变问题与平面应力问题的变量和方程都完全相同。比较一下这两个物理方程,我们就发现,将平面应力问题里面的弹性模量E换为,把平面应力问题里面的换成,这样的话,我们就从平面应变问题的物理方程就可以转化为平面应变的问题的物理方程,那么反过来也可以由平面应变问题的物理方程换成。因此在对《三角形单元悬臂梁matlab有限元编程》课程代码进行修改的时候,要注意将平面应变问题的材料刚度矩阵,改为平面应变问题的材料刚度矩阵。当然这是针对弹性问题的求解,如果对于材料非线性问题,平面应力应变刚度矩阵是变换的,其本构方程直接采用公式1-3所示的方程来定义。

图3 平面应力问题和平面应变问题的区别
在掌握基于三角形单元弹性问题的求解基础知识后,针对本案例的纯材料非线性问题,其几何方程、平衡方程的建立均为线性关系,只有物理方程存在非线性关系,具体分析如下:属于小变形问题,因此公式2表示的几何关系是线性的,公式3以应力形式表示的平衡条件也是线性的。引入物理方程,其一般形式为

在材料非线性问题中,应力与应变关系是非线性的,对于本案例,应力应变的关系如公式1所示。所以,以节点位移列阵表示的平衡方程不再是线性的,可以写成
![]()
上式与几何非线性的的表达式类似,因此材料非线性和几何非线性都可以用相同的迭代方法来求解。本系列课程主要介绍牛顿-拉普森法(切线刚度法)、初应力法、初应变法等三种迭代方法。这一小节围绕初应力和初应变法进行介绍。
3、初应力法
对于一般非线性材料,物理方程可以表示为
![]()
(7)
上式可由具有初应力的线弹性物理方程代替,即
相关文章:

材料非线性Matlab有限元编程:初应力法与初应变法
导读:本文主要围绕材料非线性问题的有限元Matlab编程求解进行介绍,重点围绕牛顿-拉普森法(切线刚度法)、初应力法、初应变法等三种非线性迭代方法的算法原理展开讲解,最后利用Matlab对材料非线性问题有限元迭代求解算法进行实现,展示了实现求解的核心代码。这些内容都将收…...
)
QT+OSG/osgEarth编译之八十二:osgdb_obj+Qt编译(一套代码、一套框架,跨平台编译,版本:OSG-3.6.5插件库osgdb_obj)
文章目录 一、osgdb_obj介绍二、文件分析三、pro文件四、编译实践一、osgdb_obj介绍 OBJ格式是一种标准的3D模型文件格式,它以纯文本形式存储关于3D模型的信息。这种格式最初由Wavefront Technologies为其高级可视化系统开发,后来被广泛应用于3D软件之间的数据交换。OBJ格式…...
[office] excel求乘积的公式和方法 #媒体#笔记#经验分享
excel求乘积的公式和方法 本文首先给出两个常规的excel求乘积的链接,然后再例举了一个文字和数字在同一单元格里面的excel求乘积的公式写法。 excel求乘积的方法分为两种,第一种是直接用四则运算的*来求乘积,另外一种就是使用PRODUCT乘积函数…...
OpenEuler20.03LTS SP2 上安装 OpenGauss3.0.0 单机部署过程(二)
开始安装 OpenGauss 数据库 3.1.7 安装依赖包 (说明:如果可以联网,可以通过网络 yum 安装所需依赖包,既可以跳过本步骤。如果网络无法连通,请把本文档所在目录下的依赖包上传到服务器上,手工安装后,即无需通过网络进行 Yum 安装了): 上传:libaio-0.3.111-5.oe1.x8…...

从零开始手写mmo游戏从框架到爆炸(十)— 集成springboot-jpa与用户表
导航:从零开始手写mmo游戏从框架到爆炸(零)—— 导航-CSDN博客 集成springboot-jpa,不用mybatis框架一个是方便对接不同的数据源。第二个目前规划的游戏内容可能对数据库的依赖不是很大,jpa应该肯定能满足要求了…...

Python算法题集_两两交换链表中的节点
Python算法题集_两两交换链表中的节点 题24:两两交换链表中的节点1. 示例说明2. 题目解析- 题意分解- 优化思路- 测量工具 3. 代码展开1) 标准求解【四节点法】2) 改进版一【列表操作】3) 改进版二【三指针法】4) 改进版三【递归大法】 4. 最优算法 本文为Python算法…...

米贸搜|Facebook在购物季使用的Meta广告投放流程
一、账户简化 当广告系列开始投放后,每个广告组都会经历一个初始的“机器学习阶段”。简化账户架构可以帮助AI系统更快获得广告主所需的成效。例如: 每周转化次数超过50次的广告组,其单次购物费用要低28%;成功结束机器学习阶段的…...

前端滚动组件分享
分享一个前端可视化常用的卡片列表滚动组件,常用于可视化项目左右两侧的卡片列表的滚动。效果如下图所示: 组件描述 当鼠标移入滚动区域时,滚动行为停止当鼠标再次离开时,滚动继续 源码展示 <template><div ref"…...
【linux开发工具】vim详解
📙 作者简介 :RO-BERRY 📗 学习方向:致力于C、C、数据结构、TCP/IP、数据库等等一系列知识 📒 日后方向 : 偏向于CPP开发以及大数据方向,欢迎各位关注,谢谢各位的支持 “学如逆水行舟࿰…...
Compose | UI组件(十四) | Navigation-Data - 页面导航传递数据
文章目录 前言传参流程实例说明普通方式传值定义接受参数格式定义接受参数类型获取参数传入参数传参和接受参数效果图 结合 ViewModel 传递参数定义ViewModel在 navigation 定义 ViewModel 实例,并且传入 LoginScreen传入输入框中的值,并且跳转传值获取值…...
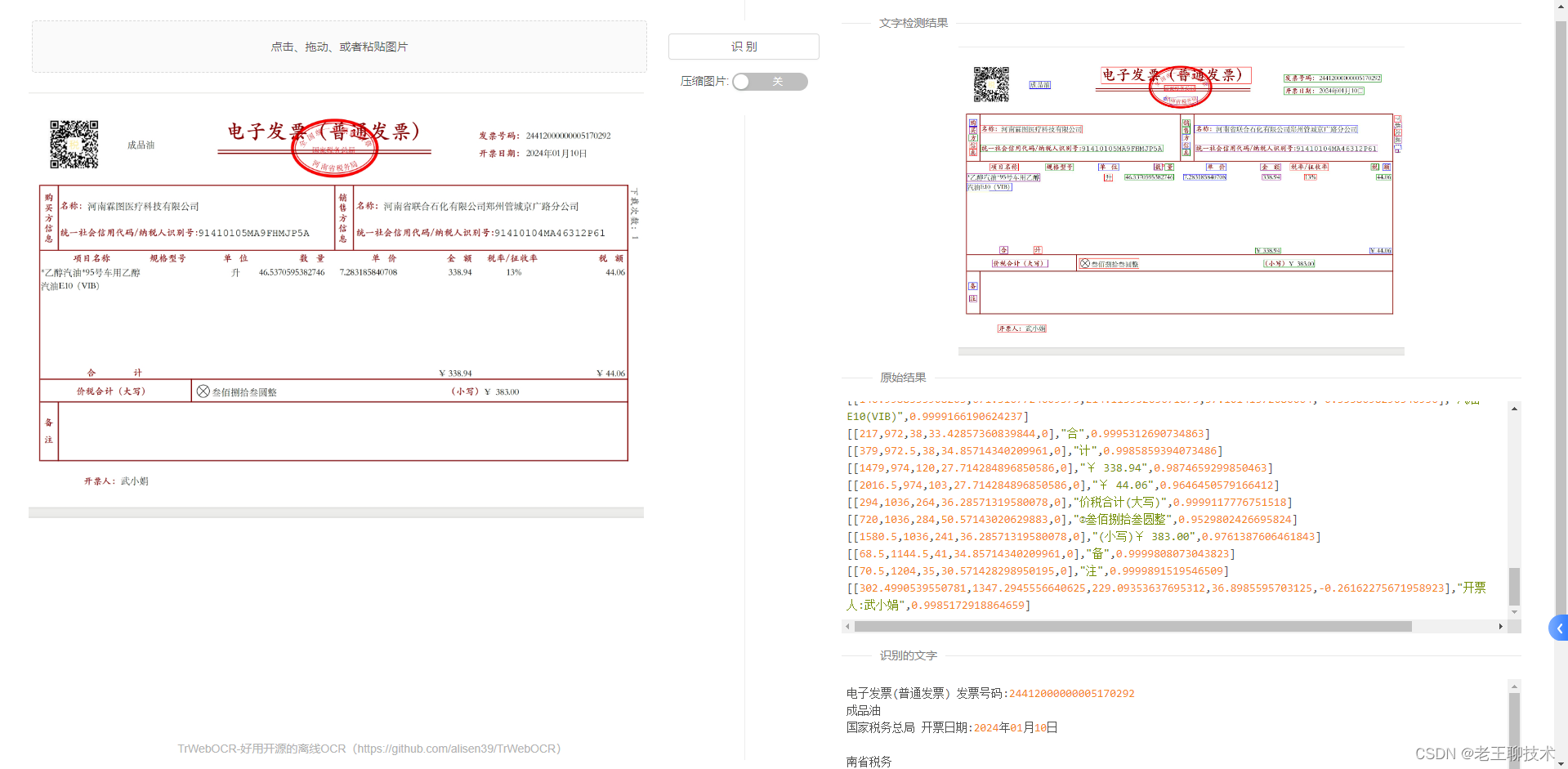
部署一个在线OCR工具
效果 安装 1.拉取镜像 # 从 dockerhub pull docker pull mmmz/trwebocr:latest 2.运行容器 # 运行镜像 docker run -itd --rm -p 10058:8089 --name trwebocr mmmz/trwebocr:latest 使用 打开浏览器输入 http://192.168.168.110:10058/ 愉快滴使用吧...
【北邮鲁鹏老师计算机视觉课程笔记】01 introduction
1 生活中的计算机视觉 生活中的各种计算机视觉识别系统已经广泛地应用起来了。 2 计算机视觉与其他学科的关系 认知科学和神经科学是研究人类视觉系统的,如果能把人类视觉系统学习得更好,可以迁移到计算机视觉。是计算机视觉的理论基础。 算法、系统、框…...
maven依赖报错处理(或者maven怎么刷新都下载不了依赖)
maven依赖报错,或者不报错,但是怎么刷新maven都没反应,可以试一下以下操作 当下载jar的时候,如果断网,或者连接超时的时候,会自动在文件夹中创建一个名为*lastupdate的文件,当有了这个文件之后…...

[VulnHub靶机渗透] dpwwn: 1
🍬 博主介绍👨🎓 博主介绍:大家好,我是 hacker-routing ,很高兴认识大家~ ✨主攻领域:【渗透领域】【应急响应】 【python】 【VulnHub靶场复现】【面试分析】 🎉点赞➕评论➕收藏…...

Android14音频进阶:MediaPlayerService如何启动AudioTrack 下篇(五十六)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒体系统工程师系列【原创干货持续更新中……】🚀 人生格言: 人生从来没有捷径,只…...
【下】)
Python基础篇_修饰符(Decorators)【下】
上一篇:Python基础篇_修饰符(Decorators)【中】property、<attribute_name>.setter、<attribute_name>.deleter、functools.lru_cache(maxsizeNone) Python基础篇_修饰符(Decorators)【下】 Python基础篇_…...
C#,十进制展开数(Decimal Expansion Number)的算法与源代码
1 十进制展开数 十进制展开数(Decimal Expansion Number)的计算公式: DEN n^3 - n - 1 The decimal expansion of a number is its representation in base -10 (i.e., in the decimal system). In this system, each "decimal place…...
Vue3快速上手(一)使用vite创建项目
一、准备 在此之前,你的电脑,需要安装node.js,我这边v18.19.0 wangdymb 2024code % node -v v18.19.0二、创建 执行npm create vuelatest命令即可使用vite创建vue3项目 有的同学可能卡主不动,可能是npm的registry设置的问题 先看下&#x…...
使用navicat导出mysql离线数据后,再导入doris的方案
一、背景 doris本身是支持直接从mysql中同步数据的,但有时候,客户不允许我们使用doris直连mysql,此时就需要客户配合将mysql中的数据手工导出成离线文件,我们再导入到doris中 二、环境 doris 1.2 三、方案 doris支持多种导入…...

re:从0开始的CSS学习之路 1. CSS语法规则
0. 写在前面 现在大模型卷的飞起,感觉做页面的活可能以后就不需要人来做了,不知道现在还有没有学前端的必要。。。 1. HTML和CSS结合的三种方式 在HTML中,我们强调HTML并不关心显示样式,样式是CSS的工作,现在就轮到C…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...
