python巧用定理判断素数
目录
判断一个数n是否是素数
求一个数的素因数个数
求大于等于指定数的最小素数
在数论中有三个非常重要的关于素数的定理
1、任何数都可以表示成若干个素数的乘积
2、任意数的素因子一个大于根号n的自然数,另一个与其对应的因子则必小于根号n。
3、除了2和3以外的所有素数都是6k±1型(k=1、2、3、...),这里要反过来是不成立的,也就是说6k±1型的不一定都是素数,例如35是6k-1型,但它不是素数
判断一个数n是否是素数
方法1:遍历从2到n-1的所有因子,时间复杂度
def is_prime(n):if n < 2: # 小于2的肯定不是素数return 0for i in range(2, n):if n % i == 0: #如果存在2到n的因子,则不是素数return 0return 1 #如果2到n遍历完后都没有,则是素数方法2:使用性质2,我们其实可以只遍历从2到根号n,此时时间复杂度降为
def is_prime(n):if n < 2: # 小于2的肯定不是素数return 0for i in range(2, int(n**0.5)+1): #这里int会向下取整,所以加1消除误差if n % i == 0: return 0return 1 方法3:使用性质2和性质3,从2到根号n,然后每隔6个数遍历,此时时间复杂度降为
def is_prime(n):if n < 2: return 0if n <= 3: # 2或3肯定是素数return 1if n % 2 == 0 or n % 3 == 0: # 如果能整除2或3,则不是素数return 0for i in range(5, int(n ** 0.5) + 1, 6):#从5开始,步长为6if n % i == 0 or n % (i + 2) == 0: # i表示6k-1,i+2表示6k+1return 0return 1
求一个数的素因数个数
根据定理1,任意数都可以表示为若干个素数的乘积,写一个程序,要求计算一个数的素因子个数
题目链接
https://www.lanqiao.cn/problems/2155/learning/?page=1&first_category_id=1&sort=students_count&category_id=3&name=%E8%B4%A8%E5%9B%A0%E6%95%B0
ans = 0
n = int(input())
# 2和3单独讨论
for i in [2, 3]:if n % i == 0: # 如果可以整除i,即含有素因子ians = ans + 1 # 计数加1while n % i == 0: # 将n一直除以i,直到n中没有因子in = n // ifor i in range(5, int(n ** 0.5) + 1, 6): for j in [i, i + 2]: # j分别表示6k-1和6k+1# 以下过程与上面同理if n % j == 0:ans = ans + 1while n % j == 0:n = n // jif n != 1: # 如果最后除出来结果不是1,说明还剩个素因数,还需要再加1ans = ans + 1print(ans)
输入396,结果为3,因为396有2、3、11三个素因子

求大于等于指定数的最小素数
def is_prime(n):if n < 2:return 0if n <= 3:return 1if n % 2 == 0 or n % 3 == 0:return 0for i in range(5, int(n ** 0.5) + 1, 6):if n % i == 0 or n % (i + 2) == 0:return 0return 1n = int(input())if is_prime(n): # 如果是素数则直接输出print(n)
else:for j in range(1, 7): # 根据性质,最多隔6位肯定会有素数,所以一直给n加1,直到n是素数则输出n = n + 1if is_prime(n):print(n)break输入17

输入35

相关文章:

python巧用定理判断素数
目录 判断一个数n是否是素数 求一个数的素因数个数 求大于等于指定数的最小素数 在数论中有三个非常重要的关于素数的定理 1、任何数都可以表示成若干个素数的乘积 2、任意数的素因子一个大于根号n的自然数,另一个与其对应的因子则必小于根号n。 3、除了2和3以…...

2023年总结
人们总说时间会改变一切,但事实上你得自己来。 今年开始给自己的时间读书、工作、生活都加上一个2.0的release版本号,相比过去的一年还是有很多进步的。 就跟git commit一样,一步一步提交优化,年底了发个版本。用李笑来的话说&am…...
Git中为常用指令配置别名
目录 1 前言 2 具体操作 2.1 创建.bashrc文件 2.2 添加指令 2.3 使其生效 2.4 测试 1 前言 在Git中有一些常用指令比较长,当我们直接输入,不仅费时费力,还容易出错。这时候,如果能给其取个简短的别名,那么事情就…...

STM32内部Flash
目录 一、内部Flash简介 二、内部Flash构成 1. 主存储器 2. 系统存储区 3. 选项字节 三、内部Flash写入过程 1. 解锁 2. 页擦除 3. 写入数据 四、工程空间分布 某工程的ROM存储器分布映像: 1. 程序ROM的加载与执行空间 2. ROM空间分布表 一、内部Flash…...

html5 audio video
DOMException: play() failed because the user didn‘t interact with the document first.-CSDN博客 不可用: 可用: Google Chrome Close AutoUpdate-CSDN博客...
LoveWall v2.0Pro社区型校园表白墙源码
校园表白墙,一个接近于社区类型的表白墙,LoveWall。 源码特色; 点赞, 发评论, 发弹幕, 多校区, 分享页, 涉及违禁物等名词进行检测! 安装教程: 环境要求;…...
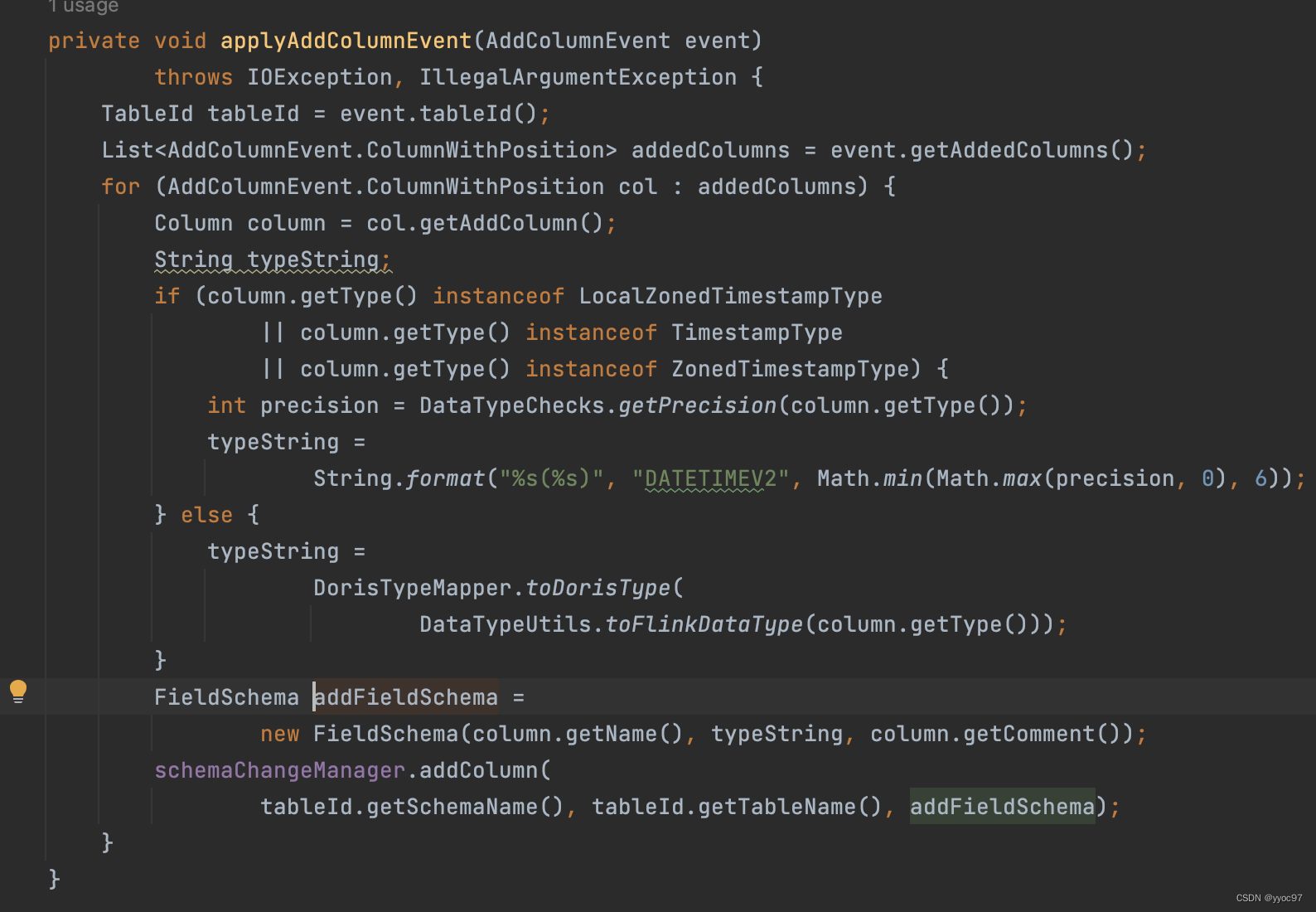
Flink cdc3.0动态变更表结构——源码解析
文章目录 前言源码解析1. 接收schema变更事件2. 发起schema变更请求3. schema变更请求具体处理4. 广播刷新事件并阻塞5. 处理FlushEvent6. 修改sink端schema 结尾 前言 上一篇Flink cdc3.0同步实例 介绍了最新的一些功能和问题,本篇来看下新功能之一的动态变更表结…...

WWW 2024 | 时间序列(Time Series)和时空数据(Spatial-Temporal)论文总结
WWW 2024已经放榜,本次会议共提交了2008篇文章,research tracks共录用约400多篇论文,录用率为20.2%。本次会议将于2024年5月13日-17日在新加坡举办。 本文总结了WWW 2024有关时间序列(Time Series)和时空数据…...

代码随想录算法——数组
目录 1、二分查找法 2、移除元素 3、有序数组的平方 4、长度最小的子数组 5、螺旋矩阵II 1、二分查找法 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在…...
Linux第45步_通过搭建“DNS服务器”学习图形化配置工具
学习的意义:通过搭建“DNS服务器”,来学习“图形化配置工具”。“DNS服务器”,我们用不到,但为后期移植linux系统服务,因为在移植系统时,需要用到这个“图形化配置工具”。 1、“menuconfig图形化配置工具…...

【Linux取经路】探寻shell的实现原理
文章目录 一、打印命令行提示符二、读取键盘输入的指令三、指令切割四、普通命令的执行五、内建指令执行5.1 cd指令5.2 export指令5.3 echo指令 六、结语 一、打印命令行提示符 const char* getusername() // 获取用户名 {return getenv("USER"); }const char* geth…...
【MATLAB】使用随机森林在回归预测任务中进行特征选择(深度学习的数据集处理)
1.随机森林在神经网络的应用 当使用随机森林进行特征选择时,算法能够为每个特征提供一个重要性得分,从而帮助识别对目标变量预测最具影响力的特征。这有助于简化模型并提高其泛化能力,减少过拟合的风险,并且可以加快模型训练和推理…...
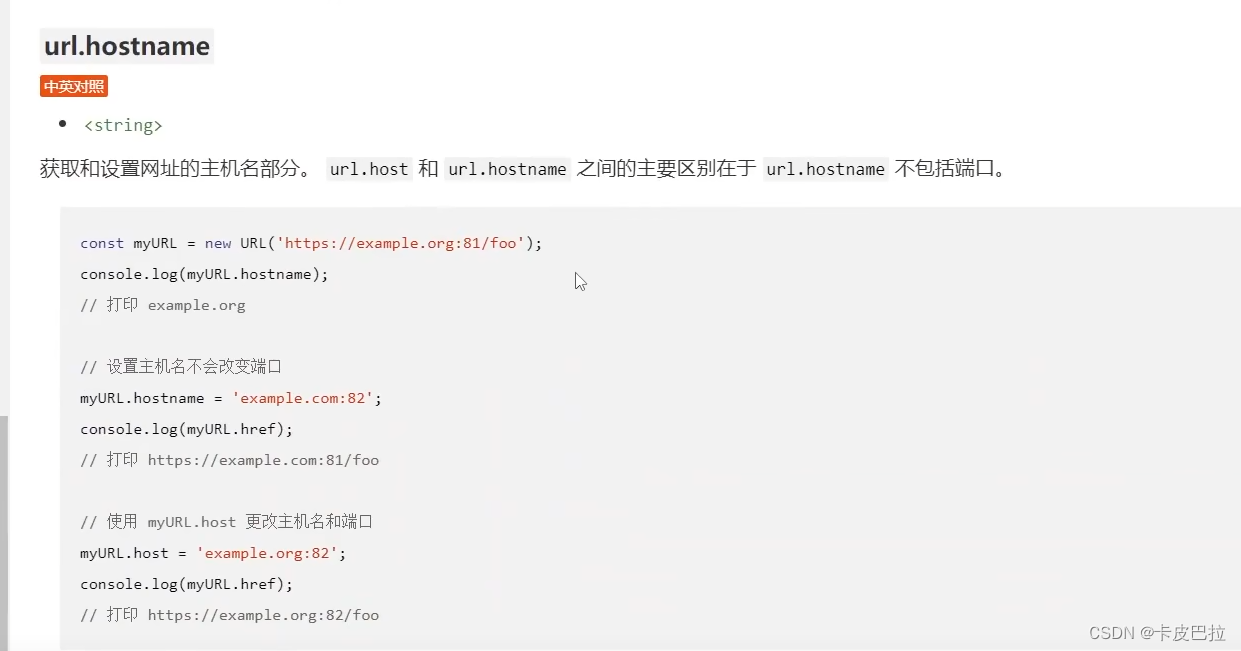
2024Node.js零基础教程(小白友好型),nodejs新手到高手,(六)NodeJS入门——http模块
047_http模块_获取请求行和请求头 hello,大家好,那第二节我们来介绍一下如何在这个服务当中来提取 HTT 请求报文的相关内容。首先先说一下关于报文的提取的方法,我在这个文档当中都已经记录好了,方便大家后续做一个快速的查阅。 …...
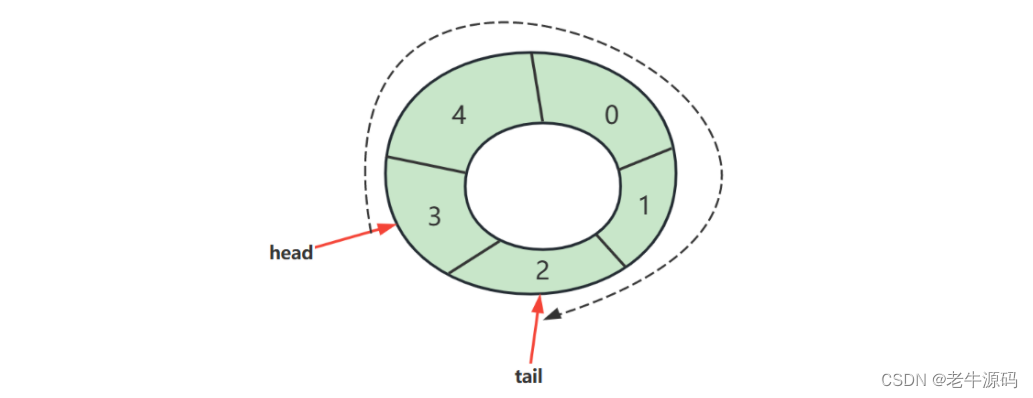
【数据结构与算法】(5)基础数据结构之队列 链表实现、环形数组实现详细代码示例讲解
目录 2.4 队列1) 概述2) 链表实现3) 环形数组实现 2.4 队列 1) 概述 计算机科学中,queue 是以顺序的方式维护的一组数据集合,在一端添加数据,从另一端移除数据。习惯来说,添加的一端称为尾,移除的一端称为头…...
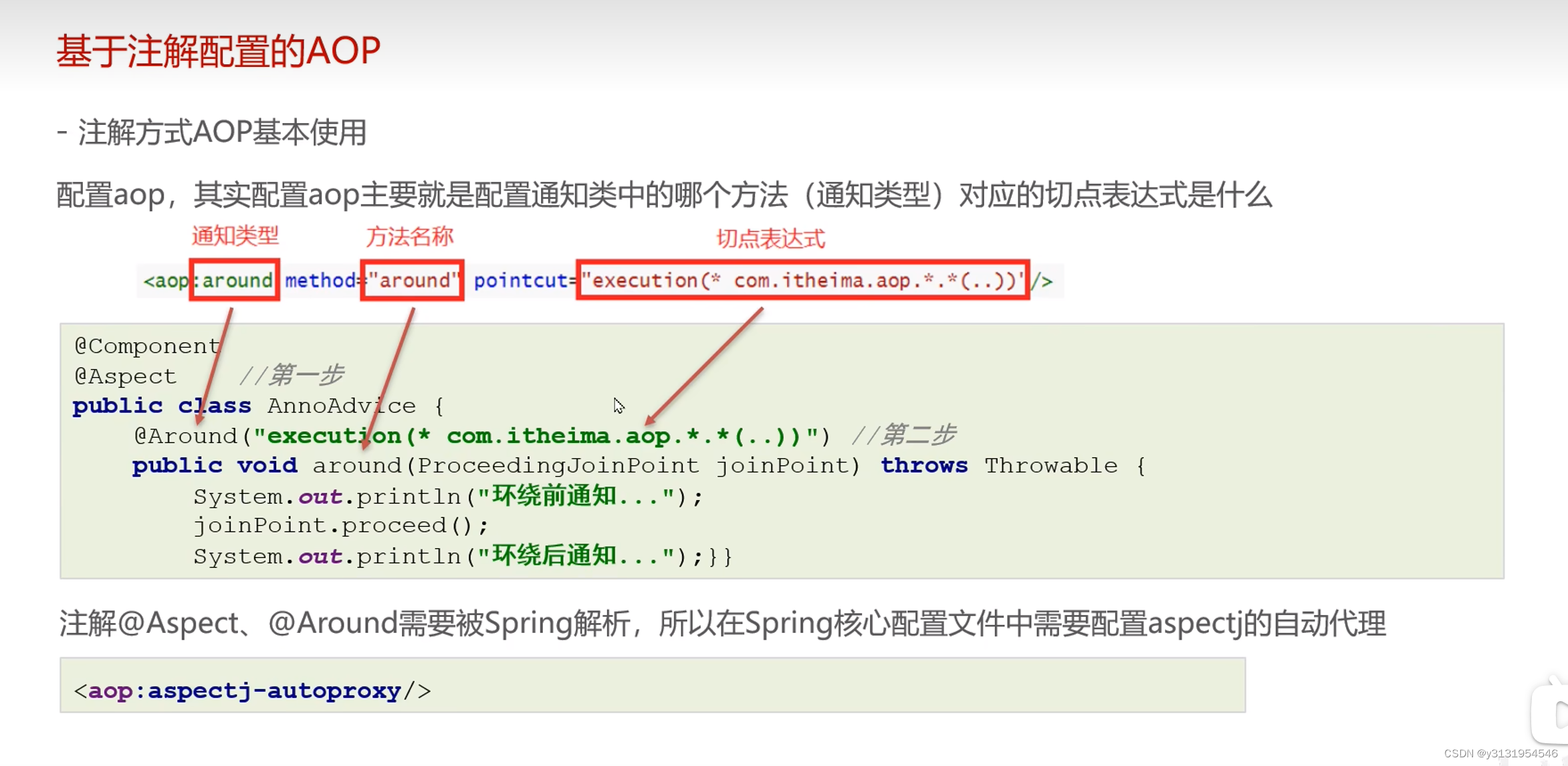
(注解配置AOP)学习Spring的第十七天
基于注解配置的AOP 来看注解式开发 : 先把目标与通知放到Spring里管理 : Service("userService") public class UserServiceImpl implements UserService {Overridepublic void show1() {System.out.println("show1......");}Overridepublic void show2…...

[C++] opencv + qt 创建带滚动条的图像显示窗口代替imshow
在OpenCV中,imshow函数默认情况下是不支持滚动条的。如果想要显示滚动条,可以考虑使用其他库或方法来进行实现。 一种方法是使用Qt库,使用该库可以创建一个带有滚动条的窗口,并在其中显示图像。具体步骤如下: 1&…...
C#用Array类的Reverse方法反转数组中元素
目录 一、Array.Reverse 方法 1.重载 2.Reverse(Array, Int32, Int32) 3. Reverse(Array) 4.Reverse(T[]) 5. Reverse(T[], Int32, Int32) 二、实例 1.Array.Reverse 方法4种重载方法综合实例 2.Reverse(Array)方法的实例 一、Array.Reverse 方法 反转一维 Array 或部…...
iOS AlDente 1.0自动防过充, 拯救电池健康度
经常玩iOS的朋友可能遇到过长时间过充导致的电池鼓包及健康度下降问题。MacOS上同样会出现该问题,笔者用了4年的MBP上周刚拿去修了,就是因为长期不拔电源的充电,开始还是电量一半的时候不接电源会黑屏无法开机,最后连着电源都无法…...

春晚刘谦魔术——约瑟夫环
昨晚,刘谦在春晚上表演了一个魔术,通过对四张撕成两半的纸牌连续操作,最终实现了纸牌的配对。 这个魔术虽然原理不是很难,但是通过刘谦精湛的表演还是让这个魔术产生了不错的效果(虽然我感觉小尼的效果更不错ÿ…...

itextpdf使用:使用PdfReader添加图片水印
gitee参考代码地址:https://gitee.com/wangtianwen1996/cento-practice/tree/master/src/test/java/com/xiaobai/itextpdf 参考文章:https://www.cnblogs.com/wuxu/p/17371780.html 1、生成带有文字的图片 使用java.awt包的相关类生成带文字的图片&…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
