DP第一天:力扣● 理论基础 ● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯
● 理论基础
DP大约五种问题:
动规基础(斐波那契数列、爬楼梯);背包问题;股票问题;打家劫舍;子序列问题。
要搞清楚:
- DP数组及其下标的含义;
- DP数组如何初始化;
- 递推公式;
- 遍历顺序;
- 打印DP数组;
无论难易,动态规划都可以用这5步来深入理解,即动规五部曲。因为对于动规,如果没有方法论的话,可能简单题目可以顺手一写就过,难一点就不知道如何下手了。
● 509. 斐波那契数
简单题也养成五部曲的习惯。
DP数组及其下标的含义:dp[i]是第i个斐波那契数。
DP数组如何初始化(dp[0]=0;dp[1]=1)、递推公式(dp[i]=dp[i-1]+dp[i-2])、遍历顺序(一层for循环,是从小到大递推所以从小到大遍历)、打印DP数组(设置n为一个不太大的数打印序列来检查正确性)这些都是直接能知道的。
代码如下:注意是返回dp[n]不是dp[n-1],所以一开始数组大小得是n+1个。
class Solution {
public:int fib(int n) {if(n==0)return 0;vector<int> dp(n+1);dp[0]=0;dp[1]=1;for(int i=2;i<=n;++i){dp[i]=dp[i-1]+dp[i-2];}return dp[n];}
};● 70. 爬楼梯
n=1,2,3,4的方法数依次是1,2,3,5(全是1步1种,一个2步3种,2个2步1种),找规律发现还是一个斐波那契额数列。所以五部曲跟上一题相同。注意dp数组初始化的元素个数和返回的下标。
class Solution {
public:int climbStairs(int n) {if(n==1)return 1;vector<int> dp(n);dp[0]=1;dp[1]=2;//初始化,下标0是n=1for(int i=2;i<n;++i){dp[i]=dp[i-1]+dp[i-2];}return dp[n-1];}
};● 746. 使用最小花费爬楼梯
五部曲:
- DP数组及其下标的含义:dp[i]是从底部(注意从0/从1开始都可以)到第i层的最低花费。要返回的还是dp数组最后一个数dp[n]。
- DP数组如何初始化:dp[0]=0,dp[1]=0(也是0,因为可以从1开始);
- 递推公式:递推公式是要从之前的dp序列得到dp[i],所以我们要立足下标i,根据题目意思,要想到达i,有两种选择:上一节台阶跨一步,上上一节台阶跨两步。取决于两种情况哪一种花费更低,所以用min:dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])。
- 遍历顺序:仍然是从小到大;
- 打印DP数组:
发现数组下标含义、初始化、递推都是要仔细思考的,要做到一致统一。
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {if(cost.size()==1)return cost[0];int n=cost.size();vector<int> dp(n+1);dp[0]=0;//初始化dp[1]=0;for(int i=2;i<=n;++i){dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);cout<<dp[i]<<" ";//打印检查}return dp[n];//底部到n个台阶的时间}
};相关文章:

DP第一天:力扣● 理论基础 ● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯
● 理论基础 DP大约五种问题: 动规基础(斐波那契数列、爬楼梯);背包问题;股票问题;打家劫舍;子序列问题。 要搞清楚: DP数组及其下标的含义;DP数组如何初始化&#x…...

Android Studio 安装Flutter插件但是没法创建项目
Android Studio 安装Flutter插件但是没法创建项目 如果你在Android Studio已经安装了Dart、Flutter插件,但是不能创建Flutter项目。 原因是因为Android Studio的版本更新,Android APK Support这个插件没被选中。 一旦勾选这个插件之后,就能…...

新春快乐(烟花、春联)【附源码】
新春快乐 一: C语言 -- 烟花二:Python -- 春联三:Python -- 烟花四:HTML -- 烟花 一: C语言 – 烟花 运行效果: #include <graphics.h> #include <math.h> #include <time.h> #include…...

nextcloud 优化扩展
cd /config vi config.php #ONLYOFFICE allow_local_remote_servers > true, #应用商店加速 appstoreenabled > true, appstoreurl > https://www.orcy.net/ncapps/v2/, #nginx配置调优 add_header Strict-Transport-Security max-age15552000; add…...

【CSS】css如何实现字体大小小于12px?
【CSS】css如何实现字体大小小于12px? 问题解决方案transform: scale(0.5)(常用)SVG 矢量图设置text 问题 文字需要显示为12px,但是小于12px的,浏览器是显示不来的 解决方案 transform: scale(0.5)(常用࿰…...
【Langchain+Streamlit】旅游聊天机器人
【LangchainStreamlit】打造一个旅游问答AI-CSDN博客 项目线上地址,无需openai秘钥可直接体验:http://101.33.225.241:8502/ github地址:GitHub - jerry1900/langchain_chatbot: langchainstreamlit打造的一个有memory的旅游聊天机器人&…...
〖大前端 - ES6篇②〗- let和const
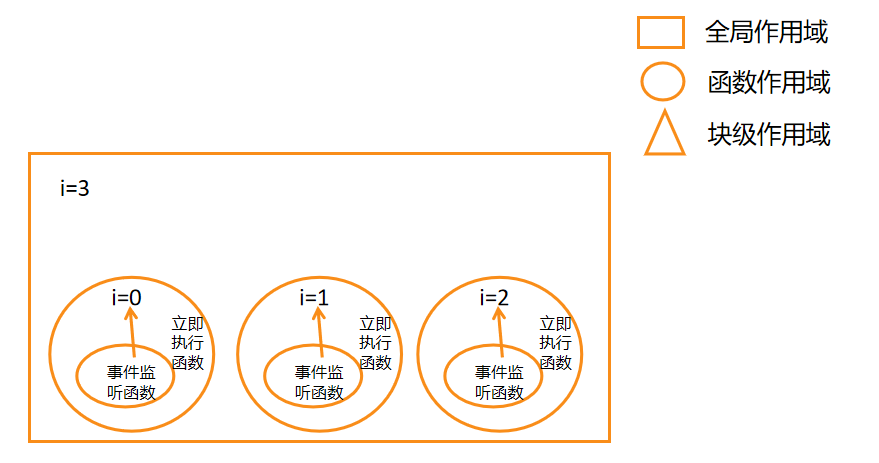
说明:该文属于 大前端全栈架构白宝书专栏,目前阶段免费,如需要项目实战或者是体系化资源,文末名片加V!作者:哈哥撩编程,十余年工作经验, 从事过全栈研发、产品经理等工作,目前在公司…...
JAVA设计模式之代理模式详解
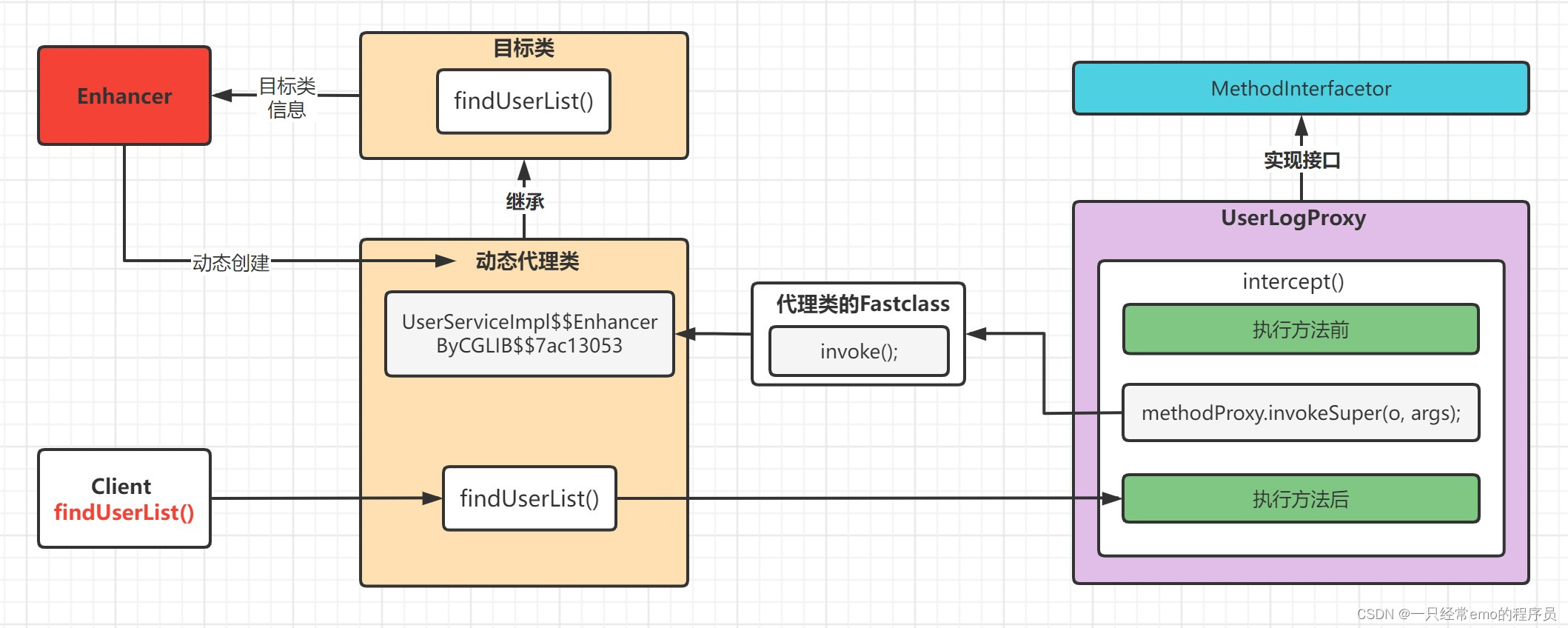
代理模式 1 代理模式介绍 在软件开发中,由于一些原因,客户端不想或不能直接访问一个对象,此时可以通过一个称为"代理"的第三者来实现间接访问.该方案对应的设计模式被称为代理模式. 代理模式(Proxy Design Pattern ) 原始定义是:让你能够提供对象的替代…...
vivo发布2023 年度科技创新;阿里全新AI代理,可模拟人类操作手机
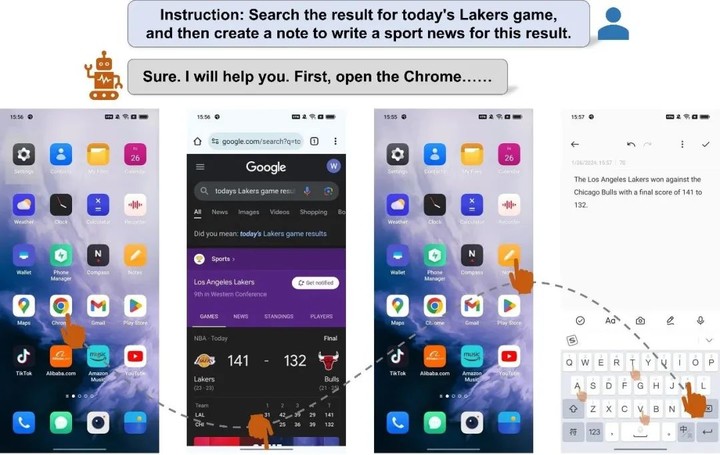
vivo 发布 2023 年度十大产品技术创新 近日,vivo 发布了「2023 年度科技创新」十大产品技术创新榜单,并将这些技术分为了 4 个板块。 「四大蓝科技」为 vivo 在去年推出的全新技术品牌,涵盖蓝晶芯片技术栈、蓝海续航系统、蓝心大模型、蓝河操…...

【制作100个unity游戏之23】实现类似七日杀、森林一样的生存游戏15(附项目源码)
本节最终效果演示 文章目录 本节最终效果演示系列目录前言实现树倒下的效果拾取圆木砍树消耗卡路里斧头手臂穿模问题处理源码完结 系列目录 前言 欢迎来到【制作100个Unity游戏】系列!本系列将引导您一步步学习如何使用Unity开发各种类型的游戏。在这第23篇中&…...

python巧用定理判断素数
目录 判断一个数n是否是素数 求一个数的素因数个数 求大于等于指定数的最小素数 在数论中有三个非常重要的关于素数的定理 1、任何数都可以表示成若干个素数的乘积 2、任意数的素因子一个大于根号n的自然数,另一个与其对应的因子则必小于根号n。 3、除了2和3以…...

2023年总结
人们总说时间会改变一切,但事实上你得自己来。 今年开始给自己的时间读书、工作、生活都加上一个2.0的release版本号,相比过去的一年还是有很多进步的。 就跟git commit一样,一步一步提交优化,年底了发个版本。用李笑来的话说&am…...
Git中为常用指令配置别名
目录 1 前言 2 具体操作 2.1 创建.bashrc文件 2.2 添加指令 2.3 使其生效 2.4 测试 1 前言 在Git中有一些常用指令比较长,当我们直接输入,不仅费时费力,还容易出错。这时候,如果能给其取个简短的别名,那么事情就…...

STM32内部Flash
目录 一、内部Flash简介 二、内部Flash构成 1. 主存储器 2. 系统存储区 3. 选项字节 三、内部Flash写入过程 1. 解锁 2. 页擦除 3. 写入数据 四、工程空间分布 某工程的ROM存储器分布映像: 1. 程序ROM的加载与执行空间 2. ROM空间分布表 一、内部Flash…...

html5 audio video
DOMException: play() failed because the user didn‘t interact with the document first.-CSDN博客 不可用: 可用: Google Chrome Close AutoUpdate-CSDN博客...
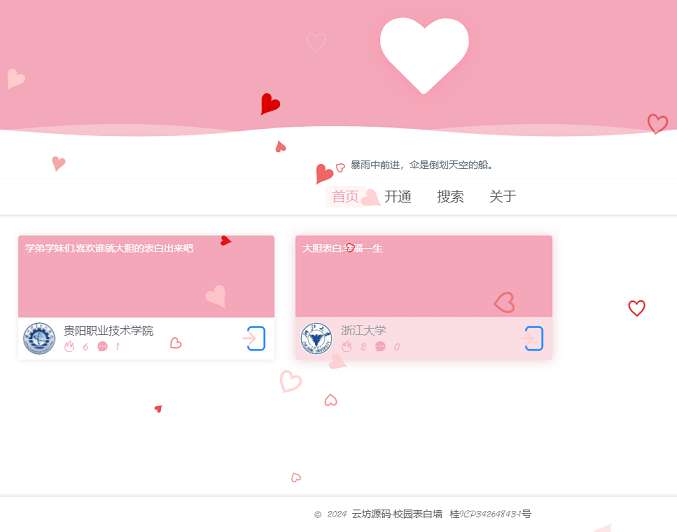
LoveWall v2.0Pro社区型校园表白墙源码
校园表白墙,一个接近于社区类型的表白墙,LoveWall。 源码特色; 点赞, 发评论, 发弹幕, 多校区, 分享页, 涉及违禁物等名词进行检测! 安装教程: 环境要求;…...
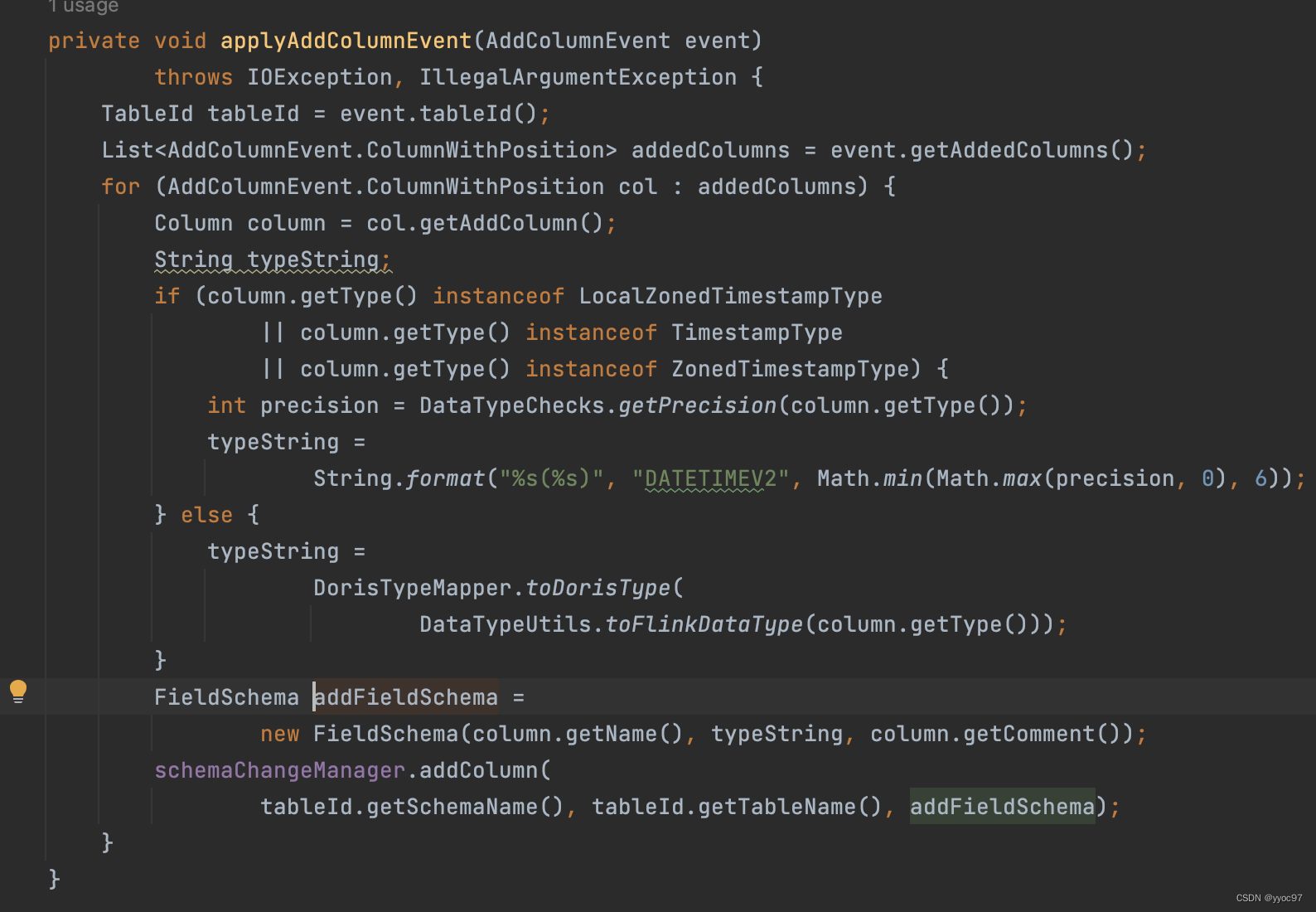
Flink cdc3.0动态变更表结构——源码解析
文章目录 前言源码解析1. 接收schema变更事件2. 发起schema变更请求3. schema变更请求具体处理4. 广播刷新事件并阻塞5. 处理FlushEvent6. 修改sink端schema 结尾 前言 上一篇Flink cdc3.0同步实例 介绍了最新的一些功能和问题,本篇来看下新功能之一的动态变更表结…...

WWW 2024 | 时间序列(Time Series)和时空数据(Spatial-Temporal)论文总结
WWW 2024已经放榜,本次会议共提交了2008篇文章,research tracks共录用约400多篇论文,录用率为20.2%。本次会议将于2024年5月13日-17日在新加坡举办。 本文总结了WWW 2024有关时间序列(Time Series)和时空数据…...

代码随想录算法——数组
目录 1、二分查找法 2、移除元素 3、有序数组的平方 4、长度最小的子数组 5、螺旋矩阵II 1、二分查找法 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在…...
Linux第45步_通过搭建“DNS服务器”学习图形化配置工具
学习的意义:通过搭建“DNS服务器”,来学习“图形化配置工具”。“DNS服务器”,我们用不到,但为后期移植linux系统服务,因为在移植系统时,需要用到这个“图形化配置工具”。 1、“menuconfig图形化配置工具…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...
