《剑指 Offer》专项突破版 - 面试题 38、39 和 40 : 通过三道面试题详解单调栈(C++ 实现)
目录
面试题 38 : 每日温度
面试题 39 : 直方图最大矩形面积
方法一、暴力求解
方法二、递归求解
方法三、单调栈法
面试题 40 : 矩阵中的最大矩形
面试题 38 : 每日温度
题目:
输入一个数组,它的每个数字是某天的温度。请计算每天需要等几天才会出现更高的温度。例如,如果输入数组 [35, 31, 33, 36, 34],那么输出为 [3, 1, 1, 0, 0]。由于第 1 天的温度是 35℃,要等 3 天才会出现更高的温度 36℃,因此对应的输出为 3。第 4 天的温度是 36℃,后面没有更高的温度,它对应的输出是 0。其他的以此类推。
分析:
解决这个问题的直观方法很多人很快就能想到。对于数组中的每个温度,可以扫描它后面的温度直到发现一个更高的温度为止。如果数组包含 n 天的温度,那么这种思路的时间复杂度是 O(n^2)。
下面通过一个具体的例子来分析这个问题的规律。假设输入的表示每天的温度的数组为 [35, 31, 33, 36, 34]。第 1 天的温度是 35℃,此时还不知道后面会不会有更高的温度,所以先将它保存到一个数据容器中。第 2 天的温度是 31℃,比第 1 天温度低,同样也保存到数据容器中。第 3 天的温度是 33℃,比第 2 天的温度高,由此可知,第 2 天需要等 1 天才有更高的温度。
每次从数组中读取某一天的温度,并且都将其与之前的温度(也就是已经保存在数据容器中的温度)相比较。从离它较近的温度开始比较看起来是一个不错的选择,也就是后存入数据容器中的温度先拿来比较,这契合 "后进先出" 的特性,所以可以考虑用栈来实现这个数据容器。同时,需要计算出现更高温度的等待天数,存入栈中的数据应该是温度在数组中的下标。等待的天数就是两个温度在数组中的下标之差。
因此,处理到第 3 天的温度时,栈的状态为 [0, 1]。在知道第 2 天需要等 1 天将出现更高的温度之后,它就没有必要再保存在栈中,将它出栈。第 3 天的温度也需要入栈,以便和以后的温度比较,此时栈的状态为 [0, 2]。
第 4 天的温度是 36℃。从栈顶开始与之前的温度比较,它比第 3 天的温度 33℃ 高,因此第 3 天需要等 1 天就会出现更高的温度,这一天在数组中的下标 2 出栈。它也比第 1 天的温度 35℃ 高,因此第 1 天需要等 3 天才会出现更高的温度,这一天在数组中的下标 0 出现。然后将第 4 天在数组中的下标 3 入栈,以便和以后的温度比较。此时栈的状态为 [3]。最后一天的温度是 34℃,比位于栈顶的第 4 天的温度低,将其入栈,最终栈的状态是 [3, 4]。最终留在栈中的两天的后面都没有出现更高的温度。
解决这个问题的思路总结起来就是用一个栈保存每天的温度在数组中的下标。每次从数组中读取一个温度,然后将其与栈中保存的温度(根据下标可以得到温度)进行比较。如果当前温度比位于栈顶的温度高,那么就能知道位于栈顶那一天需要等待几天才会出现更高的温度。然后出栈 1 次,将当前温度与下一个位于栈顶的温度进行比较。如果栈中已经没有比当前温度低的温度,则将当前温度在数组中的下标入栈。
代码实现:
class Solution {
public:vector<int> dailyTemperatures(vector<int>& temperatures) {int n = temperatures.size();vector<int> result(n, 0);stack<int> st;for (int i = 0; i < n; ++i){while (!st.empty() && temperatures[i] > temperatures[st.top()]){result[st.top()] = i - st.top();st.pop();}
st.push(i);}return result;}
};保存在栈中的温度(通过数组下标可以得到温度)是递减排序的。这是因为如果当前温度比位于栈顶的温度高,位于栈顶的温度将出栈,所以每次入栈时当前温度一定比位于栈顶的温度低或相同。
假设输入数组的长度为 n。虽然上述代码中有一个嵌套的二重循环,但它的时间复杂度是 O(n),这是因为数组中每个温度入栈、出栈各 1 次。这种解法的空间复杂度也是 O(n)。
面试题 39 : 直方图最大矩形面积
题目:
直方图是由排列在同一基线上的相邻柱子组成的图形。输入一个由非负数组成的数组,数组中的数字是直方图中柱子的高。求直方图中最大矩形面积。假设直方图中柱子的宽都为 1。例如,输入数组 [3, 2, 5, 4, 6, 1, 4, 2],其对应的直方图如下图所示,该直方图中最大矩形面积为 12,如阴影部分所示。

分析:
矩形的面积等于宽乘以高,因此只要能确定每个矩形的宽和高,就能计算它的面积。如果直方图中一个矩形从下标为 i 的柱子开始,到下标为 j 的柱子结束,那么这两根柱子之间的矩形(含两端的柱子)的宽是 j - i + 1。矩形的高就是两根柱子之间的所有柱子最矮的高度。例如,上图中从下标为 2 的柱子到下标为 4 的柱子之间的矩形宽度是 3,矩形的高度最多只能是 4,即它们之间 3 根柱子最矮的高度。
方法一、暴力求解
如果能逐一找出直方图中所有的矩形并比较它们的面积,就能得到最大矩形面积。下面使用嵌套的二重循环遍历所有矩形,并比较它们的面积。
class Solution {
public:int largestRectangleArea(vector<int>& heights) {int maxArea = 0;for (int i = 0; i < heights.size(); ++i){int minHeight = heights[i];for (int j = i; j < heights.size(); ++j){if (heights[j] < minHeight)minHeight = heights[j];int area = minHeight * (j - i + 1);
if (area > maxArea)maxArea = area;}}return maxArea;}
};这种解法的时间复杂度是 O(n^2),空间复杂度是 O(1)。
方法二、递归求解
上图的直方图中最矮的柱子在数组中的下标是 5,它的高度是 1。这个直方图的最大矩形有以下 3 种可能:
-
第 1 种是矩形通过这根最矮的柱子。通过最矮的柱子的最大矩形的高度是 1,宽度是 7。
-
第 2 种是矩形的起始柱子和终止柱子都在最矮的柱子的左侧,也就是从下标为 0 的柱子到下标为 4 的柱子的直方图的最大矩形。
-
第 3 种是矩形的起始柱子和终止柱子都在最矮的柱子的右侧,也就是从下标为 6 的柱子到下标为 7 的柱子的直方图的最大矩形。
第 2 种和第 3 种本质上来说和求整个直方图的最大矩形面积是同一个问题,可以调用递归函数解决。
class Solution {
private:int _largestRectangleArea(vector<int>& heights, int left, int right){if (left > right)return 0;if (left == right)return heights[left];
int minHeightIndex = left;for (int i = left + 1; i <= right; ++i){if (heights[i] < heights[minHeightIndex])minHeightIndex = i;}int maxArea = heights[minHeightIndex] * (right - left + 1);int area1 = _largestRectangleArea(heights, left, minHeightIndex - 1);int area2 = _largestRectangleArea(heights, minHeightIndex + 1, right);if (area1 > maxArea)maxArea = area1;if (area2 > maxArea)maxArea = area2;return maxArea;}
public:int largestRectangleArea(vector<int>& heights) {return _largestRectangleArea(heights, 0, heights.size() - 1);}
};假设输入数组的长度为 n。如果每次都能将 n 根柱子分成两根柱子数量为 n / 2 的子直方图,那么递归调用的深度为 O(logn),整个递归算法的时间复杂度是 O(nlogn)。但如果直方图中柱子的高度是排序的(递增排序或递减排序),那么每次最矮的柱子都位于直方图的一侧,递归调用的深度就是 O(n),此时递归算法的时间复杂度也变成 O(n^2)。
递归算法的空间复杂度取决于调用栈的深度,因此平均空间复杂度是 O(logn),最坏情况下的空间复杂度是 O(n)。
方法三、单调栈法
计算以每根柱子为顶的最大矩形面积,比较这些矩形面积就能得到直方图中的最大矩形面积。
以某根柱子为顶的最大矩形,一定是从该柱子向两侧延伸直到遇到比它矮的柱子,这个最大矩形的高就是该柱子的高,最大矩形的宽是两侧比它矮的柱子中间的间隔。例如,为了求上图所示的直方图中以下标为 3 的柱子为顶的最大矩形面积,应该从该柱子开始向两侧延伸,左侧比它矮的柱子的下标是 1,右侧比它矮的柱子的下标是 5。因此,以下标为 3 的柱子为顶的最大矩形的高为 4,宽为 3(左右两侧比它矮的柱子的下标之差再减 1,即 5 - 1 - 1)。
class Solution {
public:int largestRectangleArea(vector<int>& heights) {int n = heights.size();vector<int> left(n, -1);vector<int> right(n, n);
stack<int> st;for (int i = n - 1; i >= 0; --i){while (!st.empty() && heights[i] < heights[st.top()]){left[st.top()] = i;st.pop();}st.push(i);}st = stack<int>();for (int i = 0; i < n; ++i){while (!st.empty() && heights[i] < heights[st.top()]){right[st.top()] = i;st.pop();}st.push(i);}
int maxArea = 0;for (int i = 0; i < n; ++i){int area = heights[i] * (right[i] - left[i] - 1);if (area > maxArea)maxArea = area;}return maxArea;}
};这种解法的时间复杂度是 O(n),空间复杂度也是 O(n)。
面试题 40 : 矩阵中的最大矩形
题目:
请在一个由 0、1 组成的矩阵中找出最大的只包含 1 的矩形并输出它的面积。例如,在下图的矩阵中,最大的只包含 1 的矩形如阴影部分所示,它的面积是 6。

分析:
面试题 2.4 是关于最大矩形的,这个题目还是关于最大矩形的,它们之间有没有某种联系?如果能从矩阵中找出直方图,那么就能通过计算直方图中的最大矩形面积来计算矩阵中的最大矩形面积。
直方图是由排列在同一基线上的相邻柱子组成的图形。由于题目要求矩形中只包含数字 1,因此将矩阵中上下相邻的值为 1 的格子看成直方图中的柱子。如果分别以上图中的矩阵的每行为基线,就可以得到 4 个由数字 1 的格子组成的直方图,如下图所示。
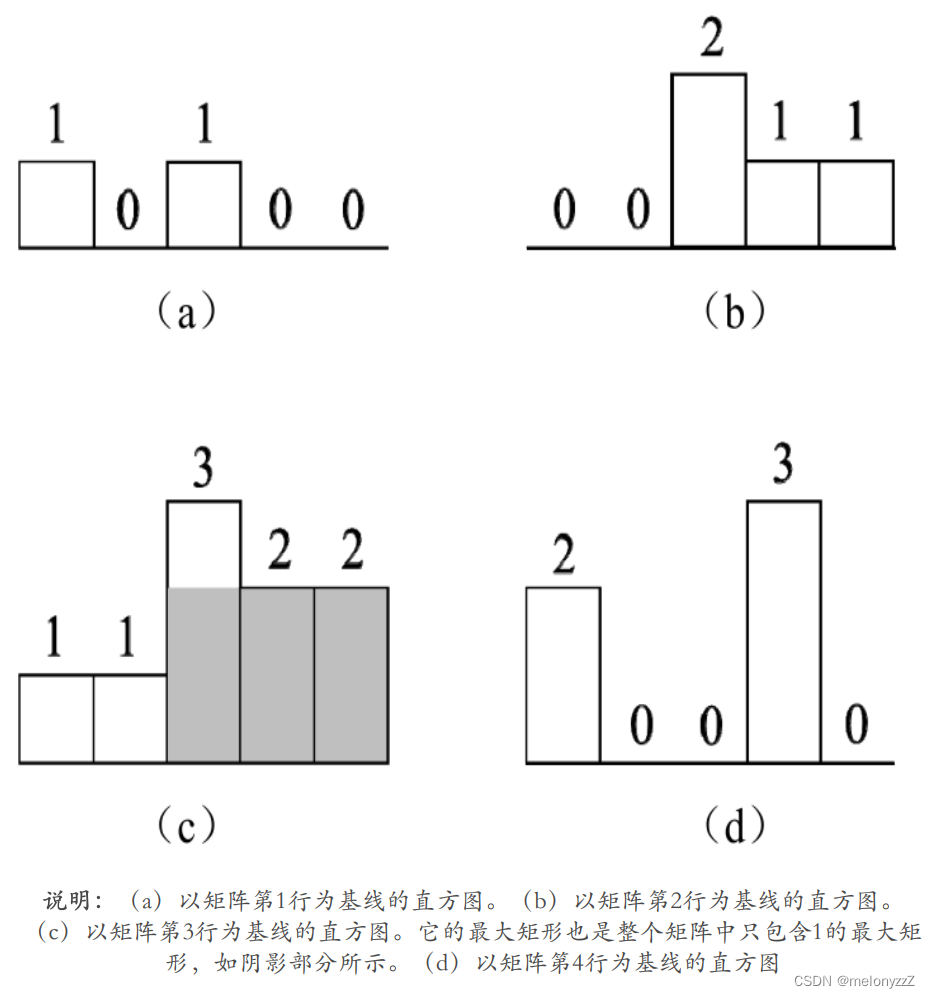
在将矩阵转换成多个直方图之后,就可以计算并比较每个直方图的最大矩形面积,所有直方图中的最大矩形就是整个矩阵中的最大矩形。
代码实现:
class Solution {
private:int largestRectangleArea(vector<int>& heights) {int n = heights.size();vector<int> left(n, -1);vector<int> right(n, n);
stack<int> st;for (int i = n - 1; i >= 0; --i){while (!st.empty() && heights[i] < heights[st.top()]){left[st.top()] = i;st.pop();}st.push(i);}st = stack<int>();for (int i = 0; i < n; ++i){while (!st.empty() && heights[i] < heights[st.top()]){right[st.top()] = i;st.pop();}st.push(i);}
int maxArea = 0;for (int i = 0; i < n; ++i){int area = heights[i] * (right[i] - left[i] - 1);if (area > maxArea)maxArea = area;}return maxArea;}public:int maximalRectangle(vector<string>& matrix) {if (matrix.size() == 0 || matrix[0].size() == 0)return 0;
int result = 0;vector<int> heights(matrix[0].size(), 0);for (int i = 0; i < matrix.size(); ++i){for (int j = 0; j < matrix[i].size(); ++j){if (matrix[i][j] == '0')heights[j] = 0;else++heights[j];}
int maxArea = largestRectangleArea(heights);if (maxArea > result)result = maxArea;}return result;}
};相关文章:

《剑指 Offer》专项突破版 - 面试题 38、39 和 40 : 通过三道面试题详解单调栈(C++ 实现)
目录 面试题 38 : 每日温度 面试题 39 : 直方图最大矩形面积 方法一、暴力求解 方法二、递归求解 方法三、单调栈法 面试题 40 : 矩阵中的最大矩形 面试题 38 : 每日温度 题目: 输入一个数组,它的每个数字是某天的温度。请计算每天需要等几天才会…...

动态规划C语言
#include <stdio.h> #include <stdlib.h> //0-1背包问题是一种经典的组合优化问题, //问题描述为:有一个给定容量的背包和一组具有不同价值和重量的物品,如何选择物品放入背包中,以使得背包中物品的总价值最大化&…...
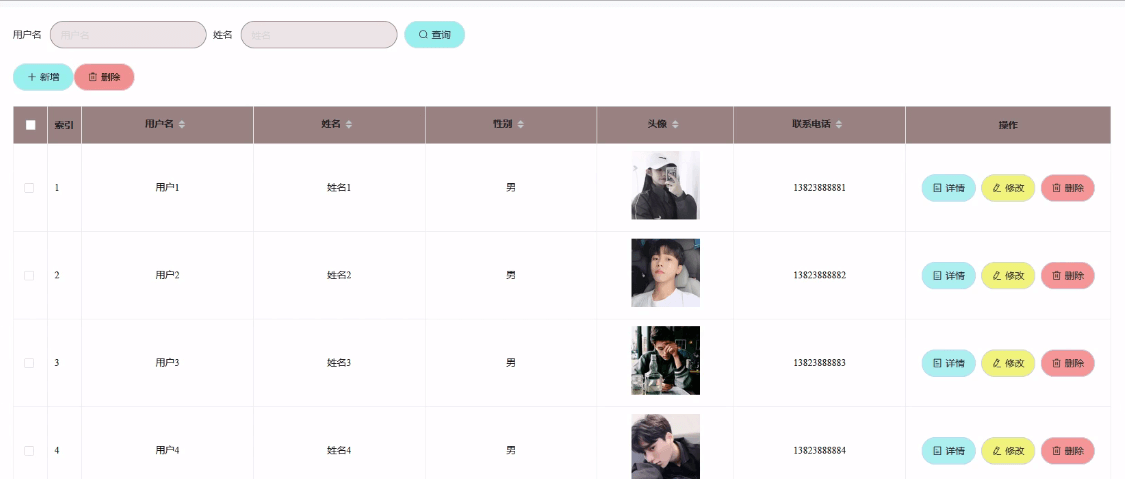
基于微信小程序的校园二手交易平台
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝12w、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...
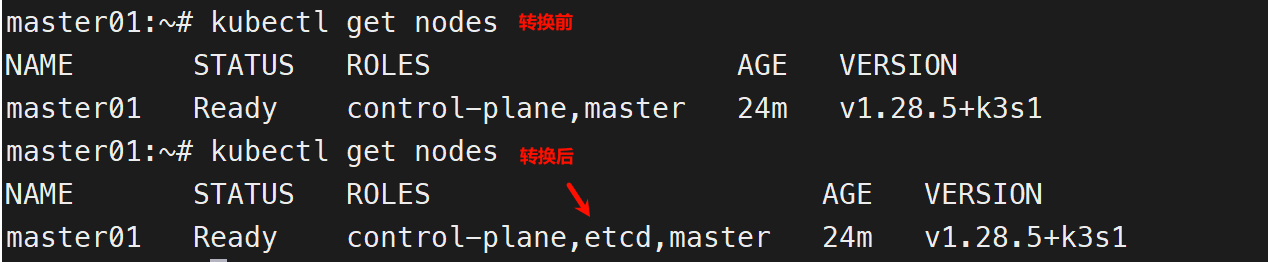
K8S系列文章之 [使用 Alpine 搭建 k3s]
官方文档:K3s - 轻量级 Kubernetes | K3s 官方描述,可运行在 systemd 或者 openrc 环境上,那就往精简方向走,使用 alpine 做系统。与 RHEL、Debian 的区别,主要在防火墙侧;其他基础配置需求类似࿰…...
计算机视觉 | OpenCV 实现手势虚拟控制亮度和音量
Hi,大家好,我是半亩花海。在当今科技飞速发展的时代,我们身边充斥着各种智能设备,然而,如何更便捷地与这些设备进行交互却是一个不断被探索的课题。本文将主要介绍一个基于 OpenCV 的手势识别项目,通过手势…...
python28-Python的运算符之三目运算符
Python可通过if语句来实现三目运算符的功能,因此可以近似地把这种if语句当成三目运算符。作为三目运算符的f语句的语法格式如下 True_statements if expression else False_statements 三目运算符的规则是:先对逻辑表达式expression求值,如果逻辑表达式…...

高德 API 10009
问题 笔者使用高德地图所提供的API接口,访问接口报错 {"info":"USERKEY_PLAT_NOMATCH","infocode":"10009","status":"0","sec_code_debug":"d41d8cd98f00b204e9800998ecf8427e"…...
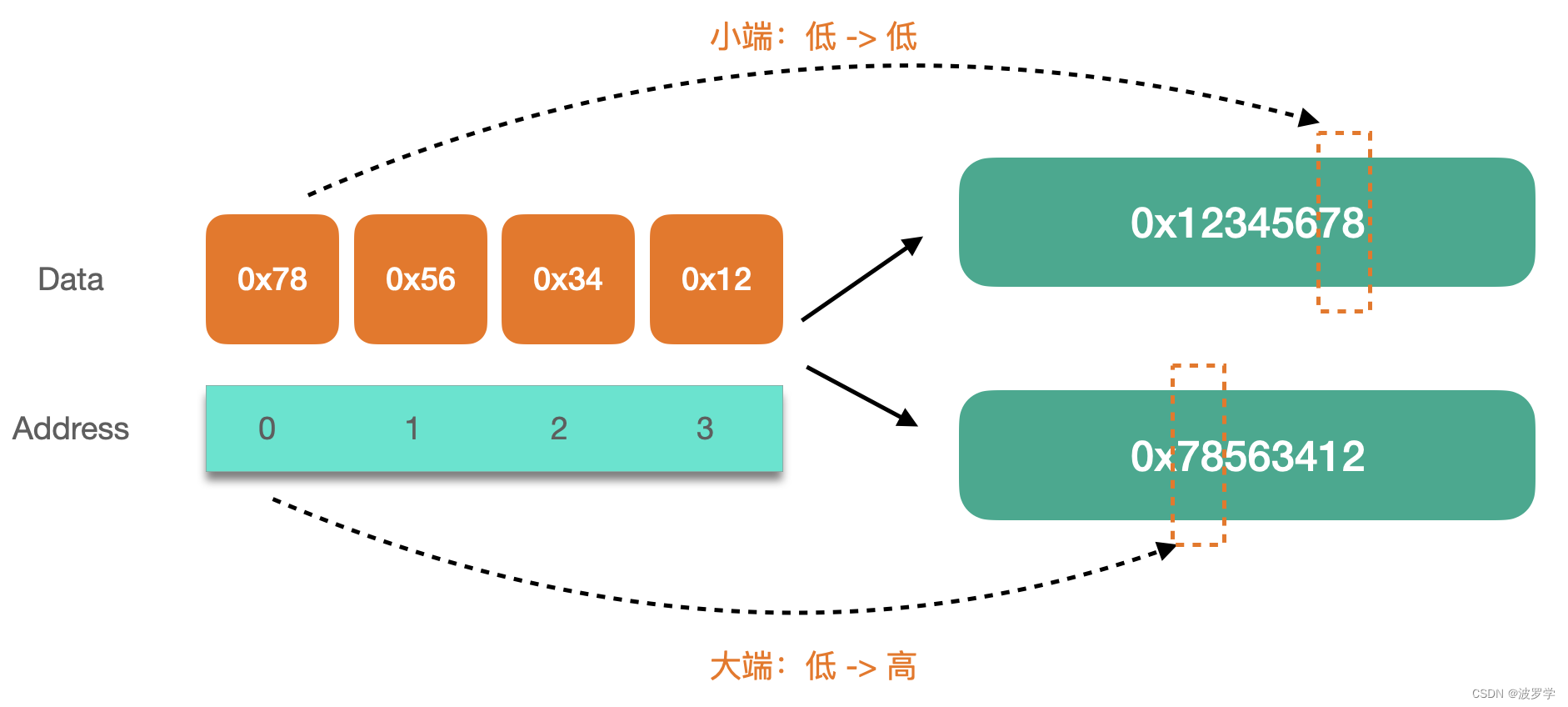
Go 语言中如何大小端字节序?int 转 byte 是如何进行的?
嗨,大家好!我是波罗学。 本文是系列文章 Go 技巧第十五篇,系列文章查看:Go 语言技巧。 我们先看这样一个问题:“Go 语言中,将 byte 转换为 int 时是否涉及字节序(endianness)&#x…...
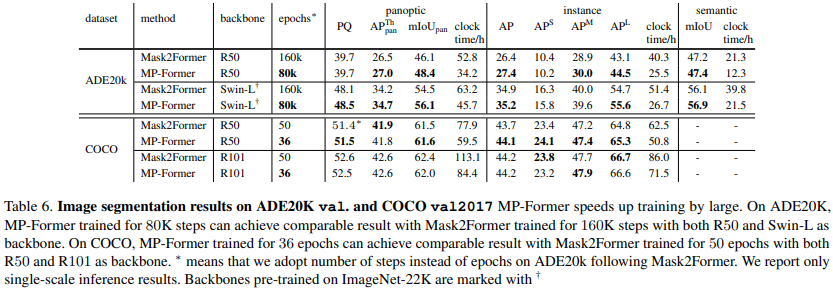
论文阅读——MP-Former
MP-Former: Mask-Piloted Transformer for Image Segmentation https://arxiv.org/abs/2303.07336 mask2former问题是:相邻层得到的掩码不连续,差别很大 denoising training非常有效地稳定训练时期之间的二分匹配。去噪训练的关键思想是将带噪声的GT坐标…...

JPEG图像的压缩标准(1)
分3个博客详细介绍JPEG图像的压缩标准,包含压缩和解压缩流程,熵编码过程和文件存储格式。 一、JPEG压缩标准概述 JPEG压缩标准由国际标准化组织 (International Organization for Standardization, ISO) 制订,用于静态图像压缩。JPEG标准包…...
数解 transformer 之 self attention transformer 公式整理
句子长度为n;比如2048,或1024,即,一句话最多可以是1024个单词。 1, 位置编码 可知,E是由n个列向量组成的矩阵,每个列向量表示该列号的位置编码向量。 2, 输入向量 加入本句话第一个单词的词嵌入向量是, 第…...

ubuntu22.04@laptop OpenCV Get Started
ubuntu22.04laptop OpenCV Get Started 1. 源由2. 步骤3. 预期&展望4. 参考资料 1. 源由 OpenCV在学校的时候接触过,不过当时专注在物理、研究方面,没有好好的学习下。 这次借后续视频分析刚性需求,对OpenCV做个入门的学习和研读&#…...
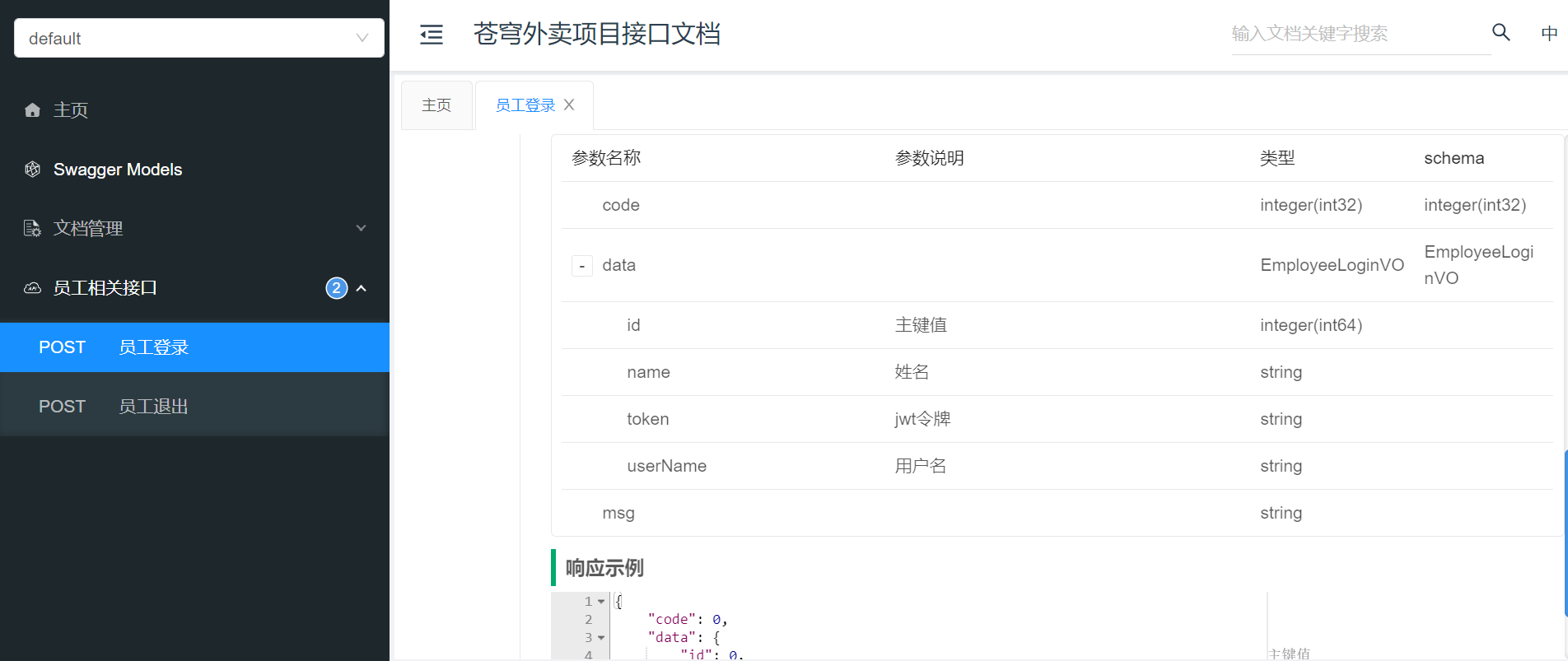
【Java】苍穹外卖 Day01
苍穹外卖-day01 课程内容 软件开发整体介绍苍穹外卖项目介绍开发环境搭建导入接口文档Swagger 项目整体效果展示: 管理端-外卖商家使用用户端-点餐用户使用当我们完成该项目的学习,可以培养以下能力: 1. 软件开发整体介绍 作为一名软件开…...

Ivanti Pulse Connect Secure VPN SSRF(CVE-2023-46805)漏洞
免责声明:文章来源互联网收集整理,请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损失,均由使用者本人负责,所产生的一切不良后果与文章作者无关。该…...

GPT-4:比ChatGPT3.5好得多,但它有多好你知道么?
GPT-4简介 GPT-4是一款由OpenAI开发的人工智能语言模型,它是ChatGPT3.5的升级版。GPT-4拥有更强大的学习能力、更高的生成质量和更广泛的知识覆盖范围,被誉为人工智能技术的重要突破。 GPT-4与ChatGPT3.5的对比 1. 学习能力 GPT-4采用了更多的神经网…...

测试:JMeter如何获取非json格式的响应参数
JMeter如何获取非json格式的响应参数 在 JMeter 中获取非 JSON 格式的响应参数通常涉及使用后置处理器来提取这些参数。以下是一些常见的方法来获取不同类型的响应数据: 正则表达式提取器: 适用于提取文本、HTML、XML 等格式中的特定文本。使用正则表达…...

2024年刘谦魔术大揭秘,其中竟用到了约瑟夫环?
目录 前言 魔术过程 揭秘过程 结尾 前言 不知道昨天春晚时刘谦的魔术大家看了没有,相信大家跟我一样也很疑惑,所以爆肝一天我得出了结论。如果你觉得还不错的话,记得点赞收藏,分享给更多的朋友看。 魔术过程 整个魔术可以分…...

openssl3.2 - update debian12‘s default openssl to openssl3.2
文章目录 openssl3.2 - update debian12s default openssl to openssl3.2概述笔记回到debian12自带的openssl版本从源码编译安装最新版的openssl配置ssl访问END openssl3.2 - update debian12’s default openssl to openssl3.2 概述 在debian12虚拟机中编译了openssl3.2(ope…...

VUE2和VUE3区别对比一览
## Vue3总结 ### 官方文档 * [Vue3](https://v3.cn.vuejs.org/api/options*data.html) * [Vue2](https://vuejs.bootcss.com/api/) ### Vue3相对于Vue2的语法特性#### 1.获取数据 * vue2 javascript export default {data() {return {name: myName,}},mounted() {console.log(t…...

Linux - updatedb 命令
1. 功能 updatedb 命令用来创建或更新slocate命令所必需的数据库文件。updatedb 命令的执行过程较长,因为在执行时它会遍历整个系统的目录树,并将所有的文件信息写入 slocate 数据库文件中。 补充说明:slocate 本身具有一个数据库ÿ…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
