排序算法---快速排序
原创不易,转载请注明出处。欢迎点赞收藏~
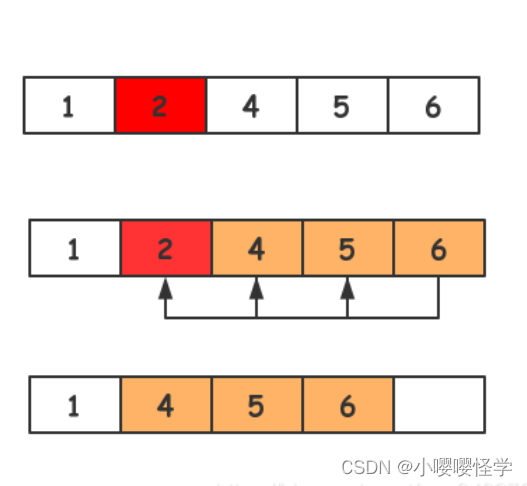
快速排序是一种常用的排序算法,采用分治的策略来进行排序。它的基本思想是选取一个元素作为基准(通常是数组中的第一个元素),然后将数组分割成两部分,其中一部分的所有元素小于等于基准值,另一部分的所有元素大于基准值。然后对这两部分继续递归应用快速排序算法,直到整个数组有序。
算法步骤如下:
- 选择基准元素。
- 将数组分割成两部分,使得左半部分的元素都小于等于基准值,右半部分的元素都大于基准值。
- 对左右两部分分别应用快速排序算法(递归)。
快速排序的时间复杂度为O(nlogn)。这是因为每次划分操作会把待排序的序列分割成两个规模大致相等的子序列,划分操作的时间复杂度为O(n),递归调用的次数为O(logn)。所以总体的时间复杂度为O(nlogn)。
快速排序的空间复杂度为O(logn)。这是因为快速排序需要使用递归来进行划分操作,每一层递归都需要额外的空间来保存分割点的位置,递归调用的次数为O(logn),所以总体的空间复杂度为O(logn)。
需要注意的是,快速排序是一种原地排序算法,它不需要额外的辅助空间来进行排序。但是在实际实现中,为了提高排序的效率和减少递归深度,通常会使用一些优化策略,比如随机选择基准元素、三数取中法等。
#include <stdio.h>// 交换函数,用于交换数组中两个元素的位置
void swap(int *a, int *b)
{int temp = *a;*a = *b;*b = temp;
}// 分割函数,用于将数组分割成左右两部分
int partition(int arr[], int low, int high)
{int pivot = arr[low]; // 选择第一个元素作为基准值int i = low, j = high;while (i < j){// 从右往左找到第一个小于基准值的元素while (i < j && arr[j] >= pivot){j--;}// 从左往右找到第一个大于基准值的元素while (i < j && arr[i] <= pivot){i++;}// 交换这两个元素的位置if (i < j){swap(&arr[i], &arr[j]);}}// 将基准值放到最终的位置swap(&arr[low], &arr[i]);return i;
}// 快速排序函数
void quick_sort(int arr[], int low, int high)
{if (low < high){// 找到分割点int pivotIndex = partition(arr, low, high);// 对分割点左右两部分进行递归排序quick_sort(arr, low, pivotIndex - 1);quick_sort(arr, pivotIndex + 1, high);}
}// 测试
int main()
{int arr[] = {8, 4, 2, 9, 5, 1, 6, 3, 7};int n = sizeof(arr) / sizeof(arr[0]);printf("排序前的数组:\n");for (int i = 0; i < n; i++){printf("%d ", arr[i]);}quick_sort(arr, 0, n - 1);printf("\n排序后的数组:\n");for (int i = 0; i < n; i++){printf("%d ", arr[i]);}putchar('\n');return 0;
}以上示例代码演示了如何使用快速排序算法对一个整数数组进行排序。首先定义了交换函数swap用于交换数组中两个元素的位置,然后定义了分割函数partition用于将数组分割成左右两部分。 最后定义了快速排序函数quick_sort来递归地进行分割和排序。
运行示例代码后,你可以看到以下输出:

相关文章:

排序算法---快速排序
原创不易,转载请注明出处。欢迎点赞收藏~ 快速排序是一种常用的排序算法,采用分治的策略来进行排序。它的基本思想是选取一个元素作为基准(通常是数组中的第一个元素),然后将数组分割成两部分,其中一部分的…...
算法||实现典型数据结构的查找、添加和删除数据 并分析其时间和空间复杂度
实现典型数据结构的查找、添加和删除数据 并分析其时间和空间复杂度 线性结构: 数组:是一种线性表数据结构,它用一组连续的内存空间,来存储一组具有相同类型的数据。 查找数据 :随机访问 流程图 /** 查询元素下标…...

【蓝桥杯冲冲冲】Invasion of the Milkweed G
【蓝桥杯冲冲冲】Invasion of the Milkweed G 蓝桥杯备赛 | 洛谷做题打卡day30 文章目录 蓝桥杯备赛 | 洛谷做题打卡day30[USACO09OCT] Invasion of the Milkweed G题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 题解代码我的一些话 [USACO09OCT] Invasion of the Mi…...

【JAVA WEB】 百度热榜实现 新闻页面 Chrome 调试工具
目录 百度热榜 新闻页面 Chrome 调试工具 --查看css属性 打开调试工具的方式 标签页含义 百度热榜 实现效果: 实现代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"vi…...
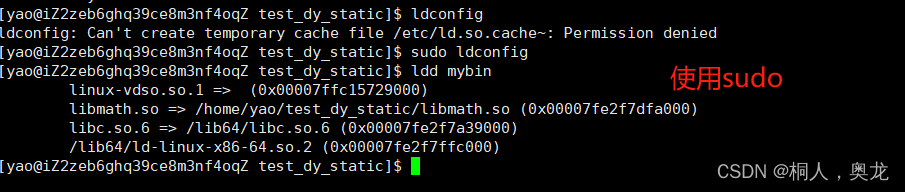
Linux——动静态库
基础知识:动vs静 类型动静加载时机运行时编译时可复用性多个文件只需要加载一份库文件每个文件都需要加载一份文件性能链接次数越多越有优势链接次数越少越有优势 代码编写 静态库 生成静态库 libmath.a:add.o sub.oar -rc $ $^%.o:%.cgcc -c $<使用静态库 头文件和工…...
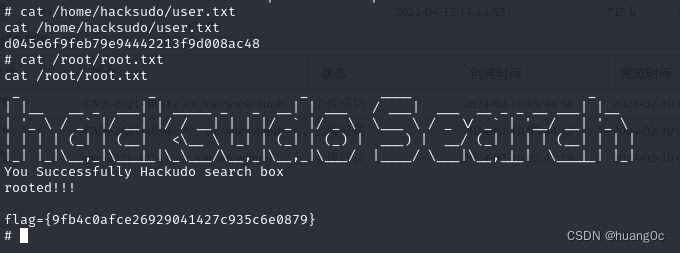
Vulnhub靶机:hacksudo-search
一、介绍 运行环境:Virtualbox 攻击机:kali(10.0.2.15) 靶机:hacksudo-search(10.0.2.50) 目标:获取靶机root权限和flag 靶机下载地址:https://download.vulnhub.co…...

Leetcode 188 买卖股票的最佳时机 IV
题意理解: 给你一个整数数组 prices 和一个整数 k ,其中 prices[i] 是某支给定的股票在第 i 天的价格。 设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说,你最多可以买 k 次,卖 k 次。 注意…...

win32编程系统BUG(Win32 API中的WM_SETTEXT消息)
由于频繁使用Win32 API中的WM_SETTEXT消息,导致内存占用直线上升。 暂未找到有效解决方案。...
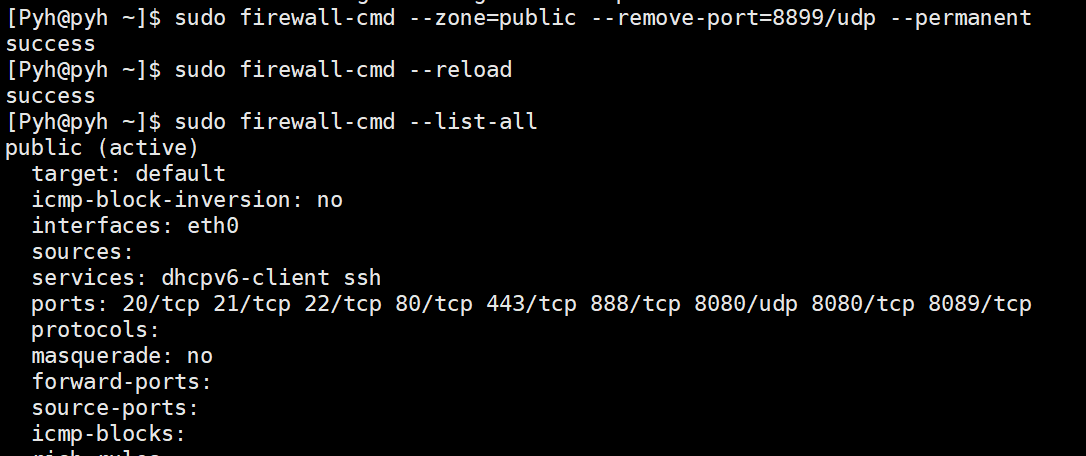
Linux防火墙开放
记录一次问题 写的网络服务无法通信 代码没问题,IP绑定、端口绑定没问题,就是无法进行通信,这里要分2步走。 服务器控制台开放 进入防火墙 添加规则,这里以开放udp的8899端口为例 这里在服务器后台就已经开放了,但此时…...
通过 docker-compose 部署 Flink
概要 通过 docker-compose 以 Session Mode 部署 flink 前置依赖 Docker、docker-composeflink 客户端docker-compose.yml version: "2.2" services:jobmanager:image: flink:1.17.2ports:- "8081:8081"command: jobmanagervolumes:- ${PWD}/checkpoin…...
HarmonyOS ArkTS修改App的默认加载的界面(二十)
前言:在Android开发中想要修改默认启动页,只需要在AndroidManifest.xml中设置即可 只需要在启动的activity种添加如下属性即可 <intent-filter><action android:name"android.intent.action.MAIN" /><category android:name&qu…...
【前端高频面试题--Vue基础篇】
🚀 作者 :“码上有前” 🚀 文章简介 :前端高频面试题 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬前端高频面试题--Vue基础篇 Vue基本原理双向绑定与MVVM模型Vue的优点计算属性与监听属性计算属性监…...

Spring Boot 实现热插拔 AOP
现在有这么一个需求:就是我们日志的开与关是交给使用人员来控制的,而不是由我们开发人员固定写死的。大家都知道可以用aop来实现日志管理,但是如何动态的来实现日志管理呢?aop源码中的实现逻辑中有这么一个步骤,就是会依次扫描Advice的实现类,然后执行。我们要做的就是自…...

2月05日,每日信息差
第一、全球首套5G及6G天地一体网络低轨试验卫星发射入轨、。据了解,“中国移动01星”是全球首颗可验证5G天地一体演进技术的试验卫星,它搭载的基站可以利用卫星的广覆盖优势把5G信号传送到地面网络无法覆盖到的地方;另外一颗“‘星核’验证星…...

使用Python进行数据的描述性分析,用少量的描述性指标来概括大量的原始数据
在进行数据分析时,当研究者得到的数据量很小时,可以通过直接观察原始数据来获得所有的信息。但是,当得到的数据量很大时,就必须借助各种描述性指标来完成对数据的描述工作。用少量的描述性指标来概括大量的原始数据,对…...
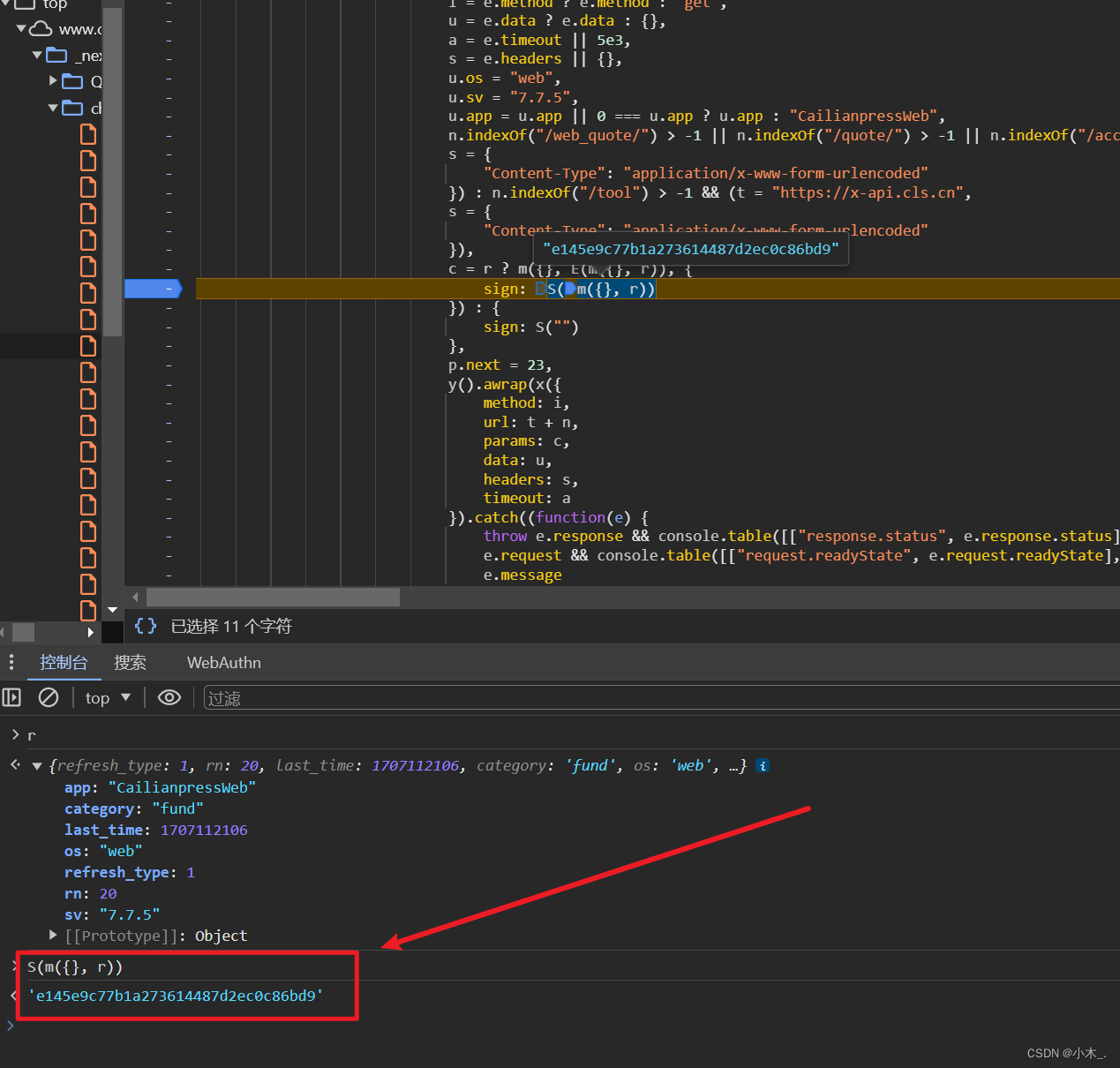
【JS逆向三】逆向某某网站的sign参数,并模拟生成仅供学习
逆向日期:2024.02.06 使用工具:Node.js 类型:webpack 文章全程已做去敏处理!!! 【需要做的可联系我】 可使用AES进行解密处理(直接解密即可):AES加解密工具 1、打开某某…...
移动光猫gs3101超级密码及改桥接模式教程
文章目录 超级管理员账号改桥接模式路由器连接光猫,PPPOE拨号即可!附录:如果需要改桥接的话不知道拨号密码咋办打开光猫Telnet功能Telnet 登录 参考文章 移动光猫吉比特GS3101超级账号获取更改桥接 移动光猫gs3101超级密码及改桥接模式教程 …...

leetcode 153
153 寻找旋转排序数组中的最小值 这道题,如果我们熟悉数组 api,可以直接用 Arrays.sort()秒杀,这个方法使用了双轴快速排序算法。 解法1如下: class Solution {public int findMin(int[] nums) {Arrays.sort(nums);return nums…...
【MySQL】数据库的基础——数据库的介绍、MySQL的介绍和架构、SQL分类、MySQL的基本使用、MySQL的存储引擎
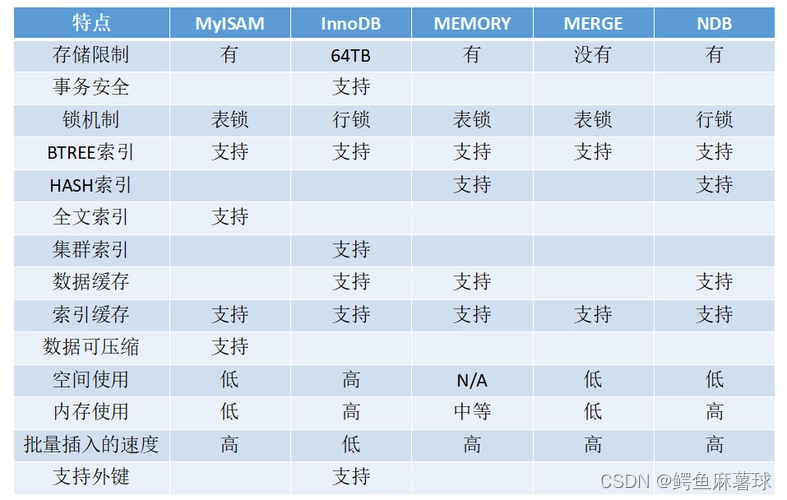
文章目录 MySQL1. 数据库的介绍1.2 主流数据库 2. MySQL的介绍2.1 MySQL架构2.2 SQL分类2.3 MySQL的基本使用2.4 MySQL存储引擎 MySQL 1. 数据库的介绍 数据库(Database,简称DB)是按照数据结构来组织、存储和管理数据的仓库。它是长期存储在计…...

后端的技术设计文档
一、 背景 1.简介 2.业务规划(非必需) 3.工作项拆解 拆解成多个工作项,每个工作项,需要多少人力。 4.资源评估(非必需) 有没有新的服务 二、架构设计 1.架构图(非必需,新服务比较需要) 2.技术选型 SpringCloud、Redis、Mysql、Myba…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...
