装箱问题+宠物小精灵之收服+数字组合——01背包
一、装箱问题 (裸题)
有一个箱子容量为 V,同时有 n 个物品,每个物品有一个体积(正整数)。
要求 n 个物品中,任取若干个装入箱内,使箱子的剩余空间为最小。
输入
第一行是一个整数 V (0 < V ≤ 20000),表示箱子容量。
第二行是一个整数 n (0 < n ≤ 30),表示物品数。
接下来 n 行,每行一个正整数(不超过10000),分别表示这 n 个物品的各自体积。
输出
一个整数,表示箱子剩余空间。
Input
24
6
8
3
12
7
9
7
Output
0
解析:
求所剩空间最小,可转化成所用空间最大。
每个物品的价值就是体积。
就可转化成 从前 n 个物品中,不超过总体积,最大价值是多少。
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=2e6+10;
int n,u;
int v[N];
int f[N];
void solve()
{cin>>u>>n;for (int i=1;i<=n;i++) cin>>v[i];for (int i=1;i<=n;i++)for (int j=u;j>=v[i];j--)f[j]=max(f[j],f[j-v[i]]+v[i]);cout<<u-f[u];
}
signed main()
{ios;int T=1;//cin>>T;while (T--) solve();return 0;
}二、 宠物小精灵之收服 (二维费用)
宠物小精灵是一部讲述小智和他的搭档皮卡丘一起冒险的故事。
一天,小智和皮卡丘来到了小精灵狩猎场,里面有很多珍贵的野生宠物小精灵。
小智也想收服其中的一些小精灵。
然而,野生的小精灵并不那么容易被收服。
对于每一个野生小精灵而言,小智可能需要使用很多个精灵球才能收服它,而在收服过程中,野生小精灵也会对皮卡丘造成一定的伤害(从而减少皮卡丘的体力)。
当皮卡丘的体力小于等于0时,小智就必须结束狩猎(因为他需要给皮卡丘疗伤),而使得皮卡丘体力小于等于0的野生小精灵也不会被小智收服。
当小智的精灵球用完时,狩猎也宣告结束。
我们假设小智遇到野生小精灵时有两个选择:收服它,或者离开它。
如果小智选择了收服,那么一定会扔出能够收服该小精灵的精灵球,而皮卡丘也一定会受到相应的伤害;如果选择离开它,那么小智不会损失精灵球,皮卡丘也不会损失体力。
小智的目标有两个:主要目标是收服尽可能多的野生小精灵;如果可以收服的小精灵数量一样,小智希望皮卡丘受到的伤害越小(剩余体力越大),因为他们还要继续冒险。
现在已知小智的精灵球数量和皮卡丘的初始体力,已知每一个小精灵需要的用于收服的精灵球数目和它在被收服过程中会对皮卡丘造成的伤害数目。
请问,小智该如何选择收服哪些小精灵以达到他的目标呢?
输入
输入数据的第一行包含三个整数:N (0 < N ≤ 1000),M (0 < M ≤ 500),K (0 < K ≤ 100),分别代表小智的精灵球数量、皮卡丘初始的体力值、野生小精灵的数量。
之后的K行,每一行代表一个野生小精灵,包括两个整数:收服该小精灵需要的精灵球的数量,以及收服过程中对皮卡丘造成的伤害。
输出
输出为一行,包含两个整数:C,R,分别表示最多收服C个小精灵,以及收服C个小精灵时皮卡丘的剩余体力值最多为R。
Input
10 100 5
7 10
2 40
2 50
1 20
4 20
Output
3 30
int n,u,k;
int v1[N],v2[N],f[N][N][N],s[N][N][N];
void solve()
{
cin>>u>>k>>n;
for (int i=1;i<=n;i++) cin>>v1[i]>>v2[i];
for (int i=1;i<=n;i++)
for (int j=1;j<=u;j++)
for (int l=1;l<k;l++)
{
f[i][j][l]=f[i-1][j][l];
s[i][j][l]=s[i-1][j][l];
if (j-v1[i]>=0&&l-v2[i]>=0)
{
if (f[i][j][l]<f[i-1][j-v1[i]][l-v2[i]]+1) f[i][j][l]=f[i-1][j-v1[i]][l-v2[i]]+1,s[i][j][l]=s[i-1][j-v1[i]][l-v2[i]]+v2[i];
else if (f[i][j][l]==f[i-1][j-v1[i]][l-v2[i]]+1&&s[i][j][l]>s[i-1][j-v1[i]][l-v2[i]]+v2[i]) s[i][j][l]=s[i-1][j-v1[i]][l-v2[i]]+v2[i];
}
}
cout<<f[n][u][k-1]<<" "<<k-s[n][u][k-1];
}
解析:
题目很长,但是能看出来是01背包问题,不过是多加了一维。
所求 从前n个小精灵中选 在不超过小智精灵球的数量,对皮卡丘的伤害值小于体力值的情况下,尽可能地多收服小精灵,最多能收服多少小精灵,和皮卡丘体力剩余最大。
正常是三维 f[i][j][k], 不过空间肯定不够,所以得优化代码,降一维就可以了。
//代码一:
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=1010;
int n,u,k;
int v1[N],v2[N],f[N][N],s[N][N];
void solve()
{cin>>u>>k>>n;for (int i=1;i<=n;i++) cin>>v1[i]>>v2[i];for (int i=1;i<=n;i++)for (int j=u;j>=v1[i];j--)for (int l=k-1;l>=v2[i];l--){if (f[j][l]<f[j-v1[i]][l-v2[i]]+1) f[j][l]=f[j-v1[i]][l-v2[i]]+1,s[j][l]=s[j-v1[i]][l-v2[i]]+v2[i];else if (f[j][l]==f[j-v1[i]][l-v2[i]]+1&&s[j][l]>s[j-v1[i]][l-v2[i]]+v2[i]) s[j][l]=s[j-v1[i]][l-v2[i]]+v2[i];}cout<<f[u][k-1]<<" "<<k-s[u][k-1];
}
signed main()
{ios;int T=1;//cin>>T;while (T--) solve();return 0;
}//代码二 (更简便)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=1010;
int n,u,k;
int v1[N],v2[N],f[N][N];
void solve()
{cin>>u>>k>>n;for (int i=1;i<=n;i++) cin>>v1[i]>>v2[i];for (int i=1;i<=n;i++)for (int j=u;j>=v1[i];j--)for (int l=k-1;l>=v2[i];l--){f[j][l]=max(f[j][l],f[j-v1[i]][l-v2[i]]+1);}cout<<f[u][k-1]<<" ";int cnt=k-1;for (int i=k-1;i>=0;i--){if (f[u][i]==f[u][k-1]) cnt=i;}cout<<k-cnt;
}
signed main()
{ios;int T=1;//cin>>T;while (T--) solve();return 0;
}三、数字组合 (方案数)
给定 N 个正整数 A1,A2,…,AN,从中选出若干个数,使它们的和为 M,求有多少种选择方案。
输入
第一行包含两个整数 N 和 M (1 ≤ N ≤ 100,1 ≤ M ≤ 10000)。
第二行包含 N 个整数,表示 A1,A2,…,AN(1 ≤ Ai ≤ 1000)。
输出
包含一个整数,表示可选方案数。
Input
4 4
1 1 2 2
Output
3
解析:
将 M 看成背包总体积
将每个数看成每个物品
所求 从前 n 个物品中选,恰好总体积是 M 的集合 的方案数。
状态转移:f[i][j]=f[i-1][j]+f[i-1][j-v[i]];
不过要记住要初始化哦!!
//代码一
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=110,M=1e4+10;
int n,m;
int v[N],f[N][M];
void solve()
{cin>>n>>m;for (int i=1;i<=n;i++) cin>>v[i];for (int i=0;i<=n;i++) f[i][0]=1; //初始化for (int i=1;i<=n;i++)for (int j=1;j<=m;j++){f[i][j]=f[i-1][j];if (j-v[i]>=0) f[i][j] +=f[i-1][j-v[i]];}cout<<f[n][m];
}
signed main()
{ios;int T=1;//cin>>T;while (T--) solve();return 0;
}//代码二 (降一维)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=1e4+10;
int n,m;
int f[N],v[N];
void solve()
{cin>>n>>m;for (int i=1;i<=n;i++) cin>>v[i];f[0]=1;for (int i=1;i<=n;i++)for (int j=m;j>=v[i];j--)f[j] +=f[j-v[i]];cout<<f[m];
}
signed main()
{ios;int T=1;//cin>>T;while (T--) solve();return 0;
}相关文章:

装箱问题+宠物小精灵之收服+数字组合——01背包
一、装箱问题 (裸题) 有一个箱子容量为 V,同时有 n 个物品,每个物品有一个体积(正整数)。 要求 n 个物品中,任取若干个装入箱内,使箱子的剩余空间为最小。 输入 第一行是一个整数 V (0 < V ≤ 20000)&…...

记一次页面接口502问题:“502 Bad Gateway”
接收别人的项目进行迭代,项目部署到服务器上之后,有一个接口数据刷不出来,一直502 后来联想到网关的问题,想通过设置白名单的方式解决,设置之后依旧不行。 查看nginx日志发现报错: *169 connect() failed …...
Oracle systemstate、gdb、dbx介绍
当数据库出现严重的性能问题或者hang了的时候, 可能最常用的办法就是重启数据库,简单有效解决问题;但是重启后如何追踪问题的根本原因成了难题,很多信息随着重启也消失不见了,让追查问题变的十分棘手,这时就…...
Stable Diffusion 模型下载:RealCartoon-Anime - V10
文章目录 模型介绍生成案例案例一案例二案例三案例四案例五案例六案例七案例八案例九案例十下载地址模型介绍 这个检查点是从 RealCartoon3D 检查点分支出来的。它的目标是产生更多的“动漫”风格,因为我喜欢动漫。:)我知道有很多人做得很好(...

课时22:内置变量_字符串相关
2.4.2 字符串相关 学习目标 这一节,我们从 基础知识、简单实践、小结 三个方面来学习 基础知识 字符串相关的变量解析 字符串计数${#file} 获取字符串的长度字符串截取 - 语法为${var:pos:length} 表示对变量var从pos开始截取length个字符,pos为…...
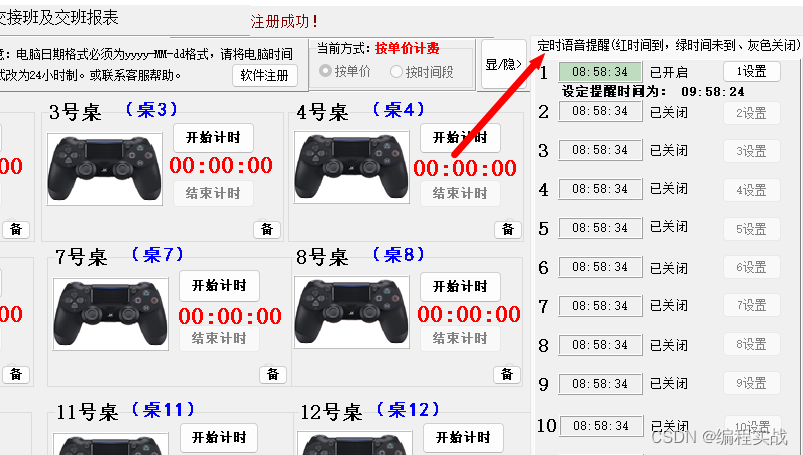
软件应用实例分享,电玩计时计费怎么算,佳易王PS5游戏计时器系统程序教程
软件应用实例分享,电玩计时计费怎么算,佳易王PS5游戏计时器系统程序教程 一、前言 以下软件教程以 佳易王电玩计时计费管理系统软件V17.9为例说明 软件文件下载可以点击最下方官网卡片——软件下载——试用版软件下载 点击开始计时后,图片…...
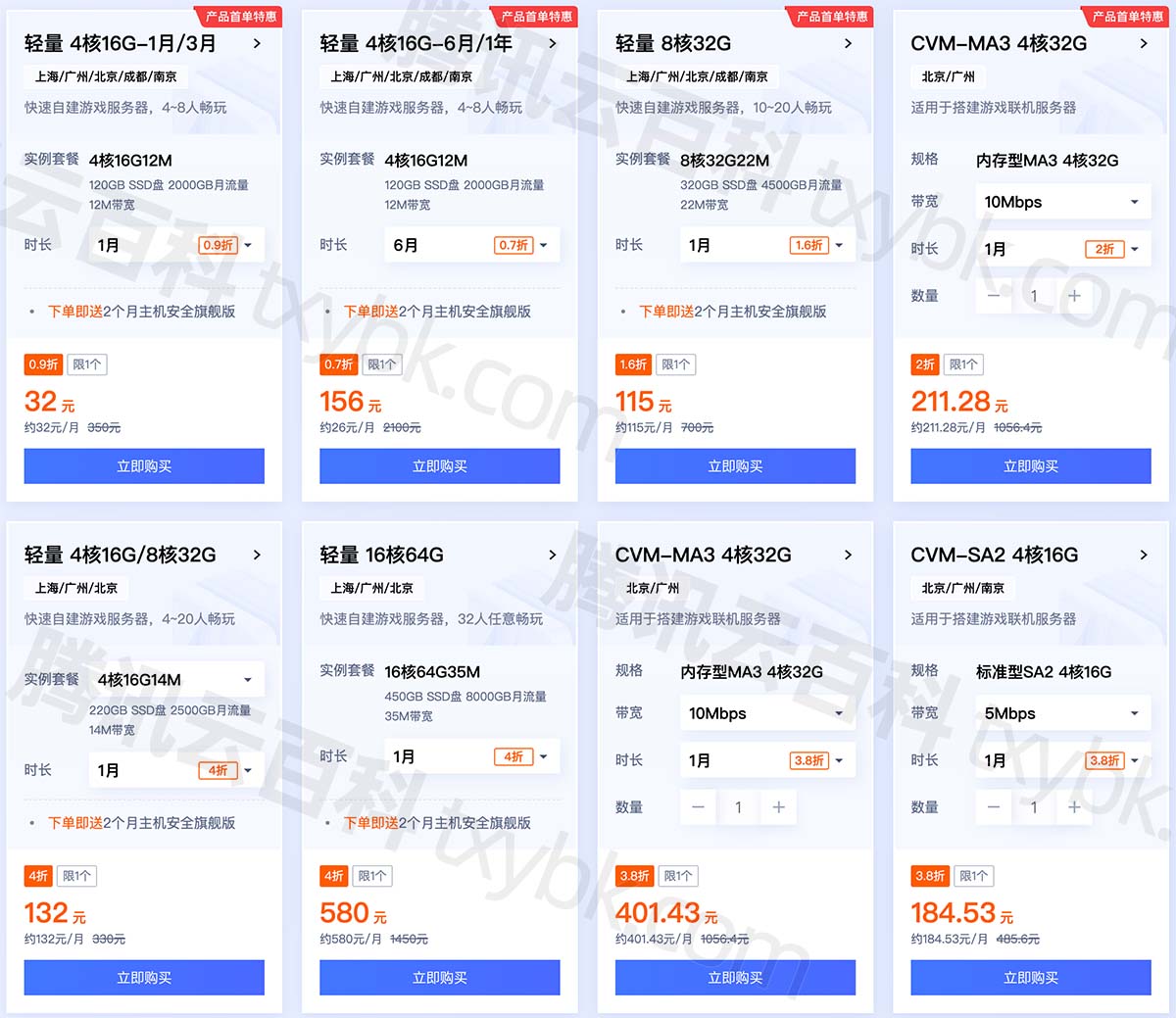
架设游戏服务器租用价格?腾讯云和阿里云价格对比
游戏服务器租用多少钱一年?1个月游戏服务器费用多少?阿里云游戏服务器26元1个月、腾讯云游戏服务器32元,游戏服务器配置从4核16G、4核32G、8核32G、16核64G等配置可选,可以选择轻量应用服务器和云服务器,阿腾云atengyu…...

ag-Grid:对数据变化的单元格进行高亮显示
对单元格高亮 问:ag-grid 当 rowData 数据变化,如何对数据变化的党员个进行高亮? 解析: 在ag-Grid中,想要对数据变化的单元格进行高亮显示,你可以使用以下步骤来实现: 监听数据变化:首先,你需要监听rowData的变化。这可以通过在你的组件中观察rowData属性的变化来实…...

Oracle 几种行转列的方式 sum+decode sum+case when pivot
目录 原始数据: 方式一: 方式二: 方式三: unpivot的使用: 原始数据: 方式一: select t_name,sum(decode(t_item, item1, t_num, 0)) item1,sum(decode(t_item, item2, t_num, 0)) item2,s…...

[AIGC] Tomcat:一个简单 and 高效的 Java Web 服务器
Tomcat(Tomcat Server)是 Apache 基金会下的一个开源项目,它是一个简单 and 高效的 Java Web 服务器,支持 Servlet 2.5、JSP 2.2 和 EL 2.2 规范。Tomcat 是当今最受欢迎的 Java Web 服务器之一,它在 Java 世界中被广泛…...
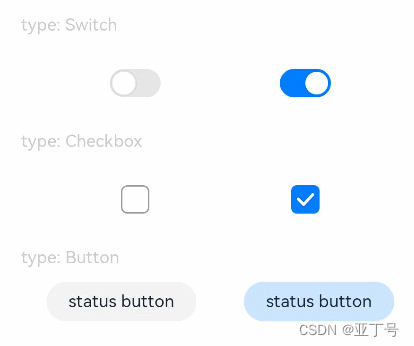
鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之Toggle组件
鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之Toggle组件 一、操作环境 操作系统: Windows 10 专业版、IDE:DevEco Studio 3.1、SDK:HarmonyOS 3.1 二、Toggle组件 组件提供勾选框样式、状态按钮样式及开关样式。 子组件 仅当Toggl…...

使用耳机壳UV树脂制作私模定制耳塞有哪些选择呢?
私模定制耳塞人士的选择可以从以下几个方面考虑: 专业经验:选择有丰富经验的私模定制耳塞人士,能够更好地理解用户需求,提供更专业的建议和服务。可以通过查看其作品和客户评价来了解其经验和口碑。材料质量:选择使用…...

什么是集群服务器
近一段时间来,集群服务器被广大站长热议,所谓集群服务器就是指很多台服务器把它们集中在一起来进行同一种服务。集群服务器也可以由很多个的计算机并行去计算,这样可以获得非常高的计算速度,提升服务器整体的工作效. 其实我们都知…...
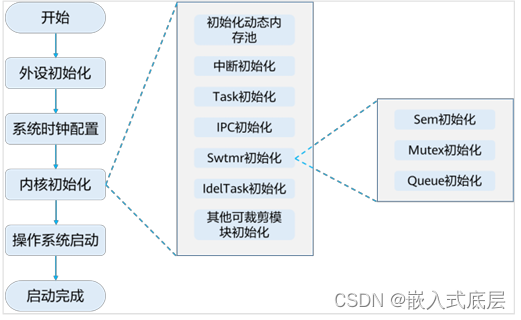
HCIA-HarmonyOS设备开发认证V2.0-3.轻量系统内核基础
目录 一、前言二、LiteOS-M系统概述三、内核框架3.1、CMSIS 和 POSIX 整体架构3.2、LiteOS-M内核启动流程 四、内核基础4.1、任务管理4.2、时间管理(待续)4.3、中断管理(待续)4.4、软件定时器(待续) 五、内存管理5.1、静态内存(待续)5.2、动态内存(待续) 六、内核通信机制6.1、…...
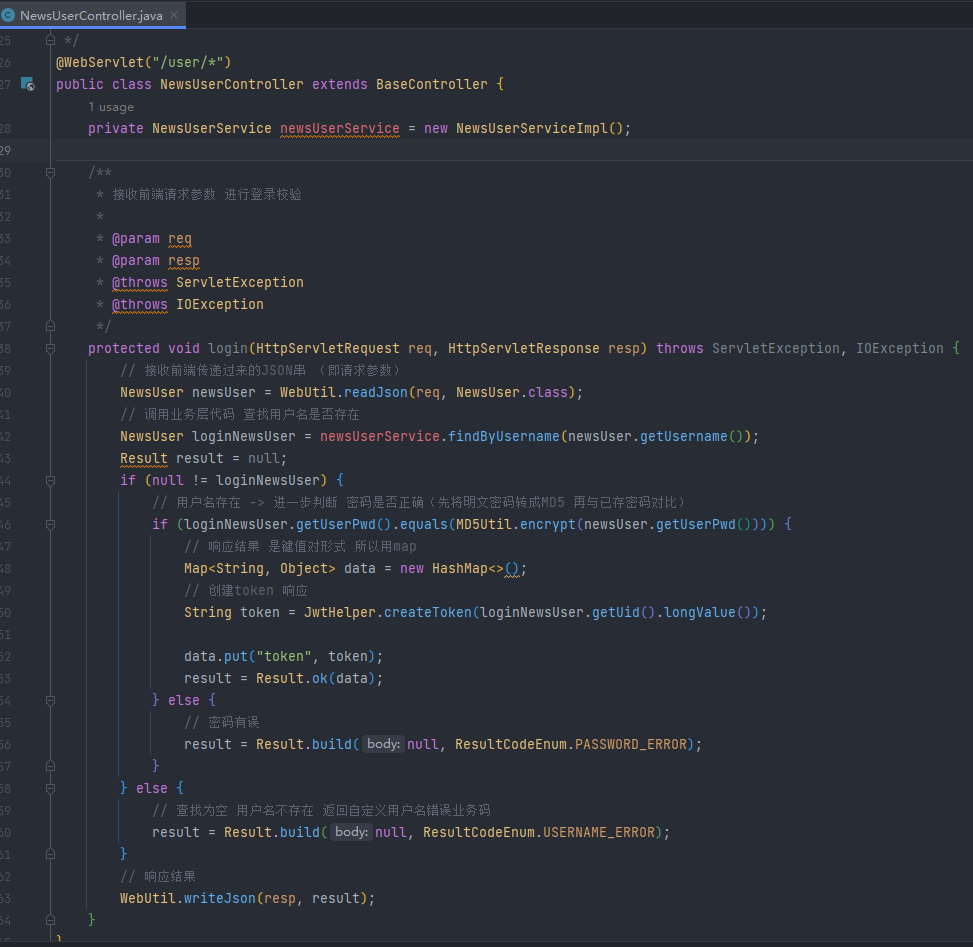
【JavaWeb】头条新闻项目实现 基本增删改查 分页查询 登录注册校验 业务功能实现 第二期
文章目录 一、为什么使用token口令二、登录注册功能2.1 登录表单提交后端代码: 2.2 根据token获取完整用户信息代码实现: 2.3 注册时用户名占用校验代码实现: 2.4 注册表单提交代码实现: 三、头条首页功能3.1 查询所有头条分类3.2…...
HiveQL——不借助任何外表,产生连续数值
注:参考文章: HiveSql一天一个小技巧:如何不借助其他任何外表,产生连续数值_hive生成连续数字-CSDN博客文章浏览阅读1.3k次。0 需求描述输出结果如下所示:12345...1001 问题分析方法一:起始值(…...
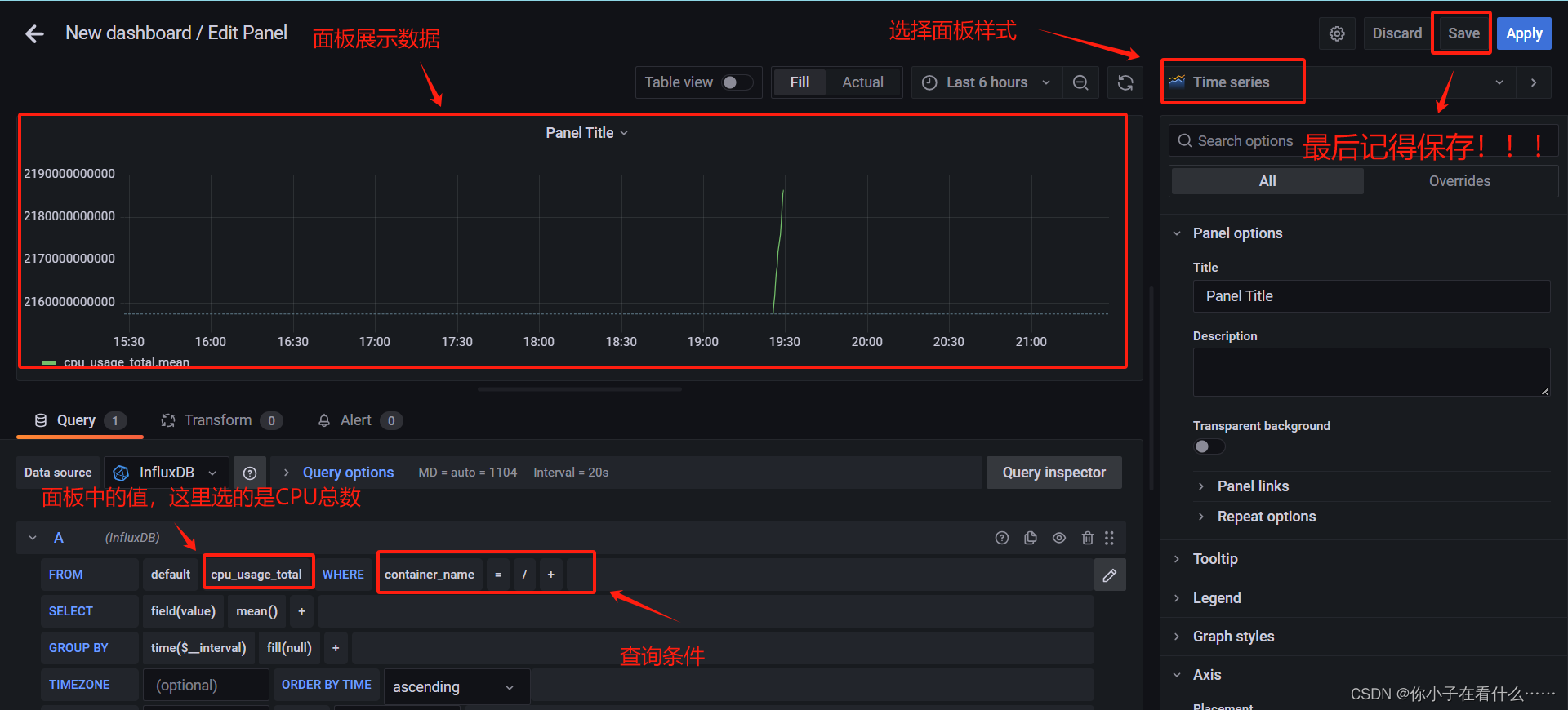
Docker容器监控-CIG
目录 一、CIG说明 1. CAdvisor 2. InfluxDB 3. Grafana 二、环境搭建 1. 创建目录 2. 编写 docker-compose.yml 3. 检查并运行容器 三、进行测试 1. 查看 influxdb 存储服务 是否能正常访问 2. 查看 cAdvisor 收集服务能否正常访问 3. 查看 grafana 展现服务&#…...

python调用golang中函数方法
一、原因说明:由于simhash方法有多种实现方式,现python中simhash方法与golang中的不一样,需要两者代码生成结果保持一致,故采用python中的代码调用golang编译的so文件来实现。 环境配置:①Windows10系统要有gcc环境&a…...

Ps:颜色取样器工具
颜色取样器工具 Color Sampler Tool允许用户从图像中设置特定的颜色取样点,然后利用“信息”面板查看该点在不同颜色模式下(包括:RGB、CMYK、Lab、灰度等)的颜色值,因此可为色彩分析、颜色校正、色彩匹配等提供精确的数…...

Rust引用、借用和所有权详解
在Rust中,引用、借用和所有权是语言的核心概念,它们共同构成了内存管理的基石。本篇博客将介绍Rust中的这些概念,并通过具体的例子深入探讨它们的用法和优势。 所有权 Rust中的所有权是一种独特的内存管理机制,它规定了在特定作…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
