Peter算法小课堂—背包问题
我们已经学过好久好久的动态规划了,动态规划_Peter Pan was right的博客-CSDN博客
那么,我用一张图片来概括一下背包问题。

大家有可能比较疑惑,优化决策怎么优化呢?答案是,滚动数组,一个神秘而简单的东西。
01背包
题目:小偷来你家,他带的包只能装c斤的财务。你家有n种财务,分别重w1、w2......wn斤,价值分别为v1、v2......,请输出能拿走的最大总价值?
大家思考一下状态定义和状态转移方程。
额……
状态定义
f[i][j]:用前i个物品,每个物品只能选或不选,满足重量和小于等于j的所有选法中,价值最高的那个方案。最终答案:f[n][c]
状态转移方程
首先,我们分两种情况讨论:1.选i 2.不选i
1。 此时我们重量和会变小w[i],但是价值会增加v[i],f[i][j]=f[i-1][j-w[i]]+v[i]
2。 此时物品数减1,f[i][j]=f[i-1][j]
最后,再取最大值,得到状态转移方程:f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i])
代码①
for(int i=1;i<=n;i++) cin>>w[i]>>v[i];
for(int i=1;i<=n;++i){for(int j=1;j<=c;++j){if(w[i]>j) f[i][j]=f[i-1][j];else f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i]);}
}
cout<<f[n][c]<<endl;有点费空间,要开滚动数组
代码②
滚动数组,给大家看个图

我们发现,dp[i][j]这一格,只需要i-1这一行,i-2、i-3……都不需要。题目如果并没有要求中间的状态(比如输出背包的方案),我们就可以将其省略来节省空间的使用。所以我们可以只用一维数组dp[j]来记录数据dp[i][j]的状态,在更新的过程中不断用新的数据dp[j] (dp[i][j]) 覆盖掉旧的数据dp[j](dp[i-1][j])。大家听懂了吗???
代码呢?
#include <bits/stdc++.h>
using namespace std;
const int MAXC=2009;
int n,c,w,v,f[MAXC];
int main(){cin>>c>>n;for(int i=1;i<=n;i++){cin>>w>>v;for(int j=c;j>=w;j--)f[j]=max(f[j],f[j-w]+v);}cout<<f[c]<<endl;return 0;
}大家可能会疑惑,为什么第二层循环要倒着推啊,我给出一个解释。我们每次计算dp[j] (即dp[i][j]) 的时候都会需要dp[j-w[i]] (即dp[i-1][j-w[i]])的值。所以如果我们正序计算,那么dp[j-w[i]]就已经更新了 (即用过之前的背包了),与每个背包只能用1次不符。那么,这不就是完全背包要的吗?
完全背包
题目:小偷来你家,他带的包只能装c斤的财务。你家有n种财务,每种数量无限多,分别重w1、w2......wn斤,价值分别为v1、v2......,请输出能拿走的最大总价值?
题解请看01背包,这里只给出代码
cin>>c>>n;
for(int i=1;i<=n;i++){cin>>w>>v;for(int j=w;j<=c;j++)f[j]=max(f[j],f[j-w]+v);
}
cout<<f[c]<<endl;分组背包


分组01与普通01的区别就是,分组01有两组策略:1.选择本组的某一件 2.一件不选

所以说,分组背包编码很麻烦
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll G=19;
const ll N=39;
const ll MAXV=209;
ll c,n,g,f[MAXV];
vector<ll> w[G],v[G];
int main(){cin>>c>>n>>g;for(ll i=1;i<=n;i++){ll ww,vv,p;cin>>ww>>vv>>p;w[p].push_back(ww);v[p].push_back(vv);}for(ll i=0;i<=g;i++){//枚举组号for(ll j=c;j>=0;j--){//枚举载重for(ll k=0;k<w[i].size();k++){//枚举物品if(j>=w[i][k]) f[j]=max(f[j],f[j-w[i][k]]+v[i][k]);}}}cout<<f[c]<<endl;return 0;
}多重背包

多重背包怎么办呢,这里,我们要采用二进制拆分。

就是……这样
void bb01(int w,int v){for(int j=c;j>=w;j--)f[j]=max(f[j],f[j-w]+v);
}
int main(){cin>>n>>c;for(int i=1;i<=n;i++){cin>>w>>v>>s;for(int k=1;k<=s;s-=k;k*=2) bb01(k*w,k*v);if(s) bb01(s*w,s*v);}cout<<f[c]<<endl;return 0;
}简单吧,其实为什么这里我都没有进行仔细的讲解,是因为……不会,再多思考思考01背包和图片。
混合背包
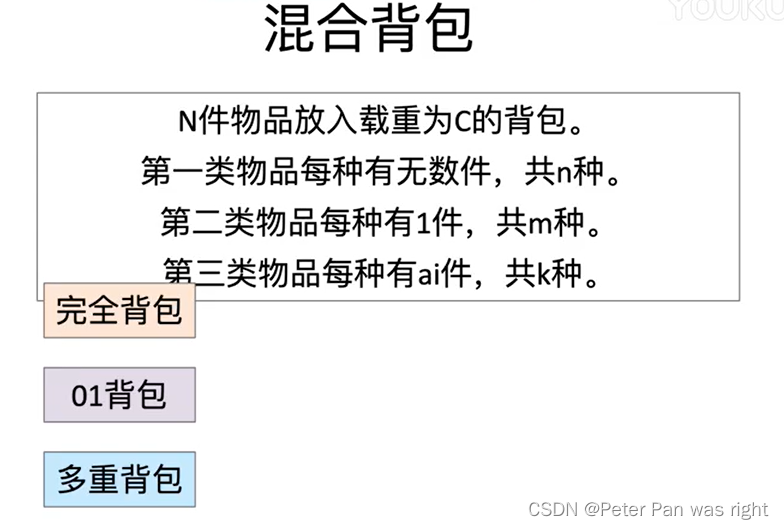
大家试着写写。大家有兴趣的话可以去往上搜搜“背包九讲”。
希望这些对大家有用,三连必回
相关文章:

Peter算法小课堂—背包问题
我们已经学过好久好久的动态规划了,动态规划_Peter Pan was right的博客-CSDN博客 那么,我用一张图片来概括一下背包问题。 大家有可能比较疑惑,优化决策怎么优化呢?答案是,滚动数组,一个神秘而简单的东西…...

网易腾讯面试题精选----50 个 Git 面试问题
介绍 Git 是 DevOps 之旅的起点。所以,我只是概述了 50 个快速问题以及 Git 的答案。这些问题非常快,你可以在 DevOps 面试中问。它适合初学者到中级水平。 面试问答 1.问:什么是Git? 答:Git 是一个分布式版本控制系统,允许多个开发人员在一个项目上进行协作并跟踪源代…...

Android CMakeLists.txt语法详解
一.CMake简介 你或许听过好几种 Make 工具,例如 GNU Make ,QT 的 qmake ,微软的 MSnmake,BSD Make(pmake),Makepp,等等。这些 Make 工具遵循着不同的规范和标准,所执行的…...

Vue3快速上手(二)VSCode官方推荐插件安装及配置
一、VSCode官方插件安装,如下图2款插件 在用vite创建的程序里,提示提安装推荐的插件了,如下图: 二、配置 在设置-扩展里找到Volar插件,将Dot Value勾选上。这样在ref()修改变量时,会自动填充.value,无需…...

等保2、3级所需设备
三级等保要求及所需设备 《等级保护基本要求》所需设备 结构安全(G3) b)应保证网络各个部分的宽带满足业务高峰期需要; g)应按照对业务服务的需要次序来指定宽带分配优先级别,保证在网络发生拥堵的时候优先保护重要主机 负载均衡…...
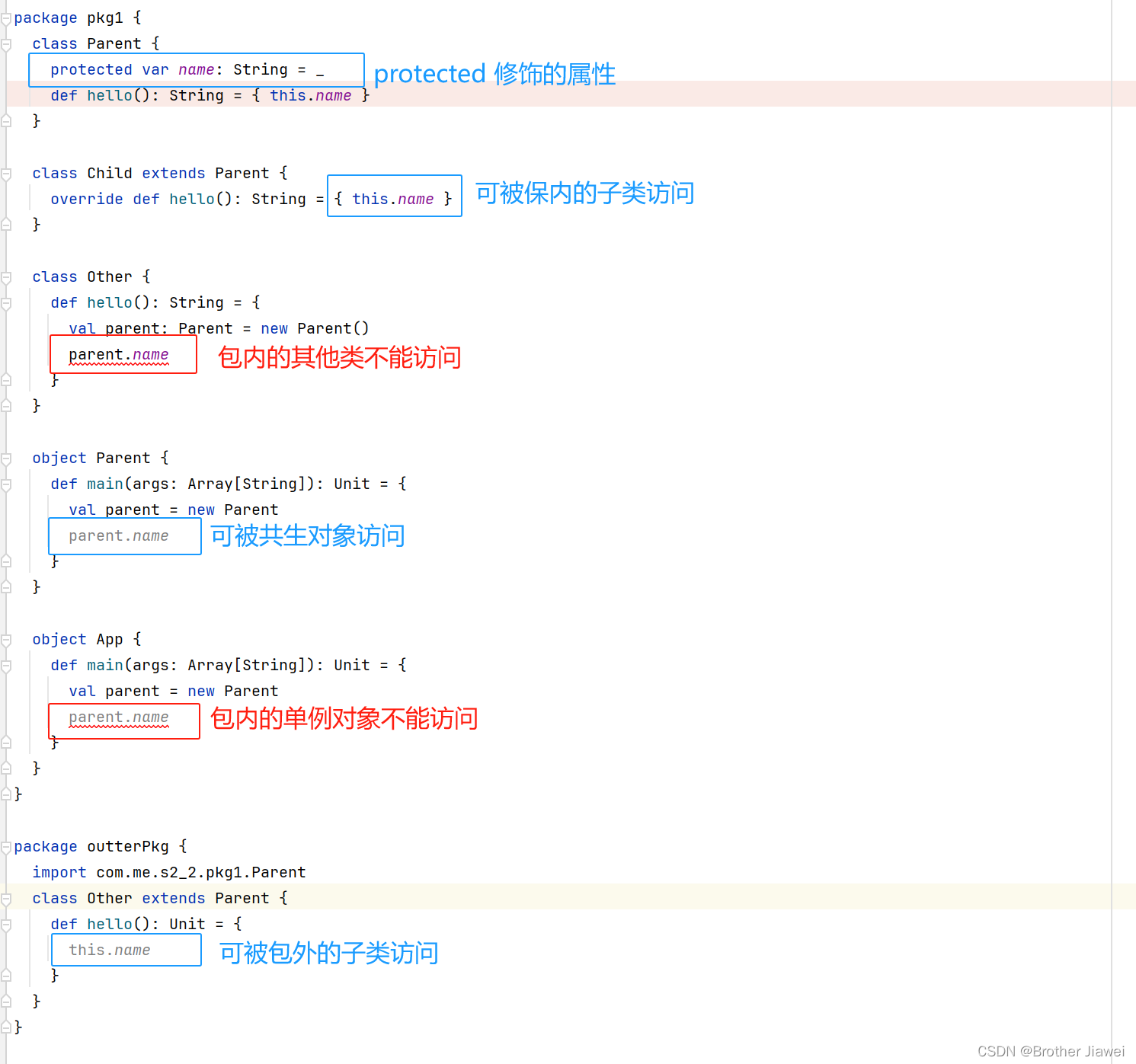
6 scala-面向对象编程基础
Scala 跟 Java 一样,是一门面向对象编程的语言,有类和对象的概念。 1 类与对象 与 Java 一样,Scala 也是通过关键字 class 来定义类,使用关键字 new 创建对象。 要运行我们编写的代码,同样像 Java 一样,…...
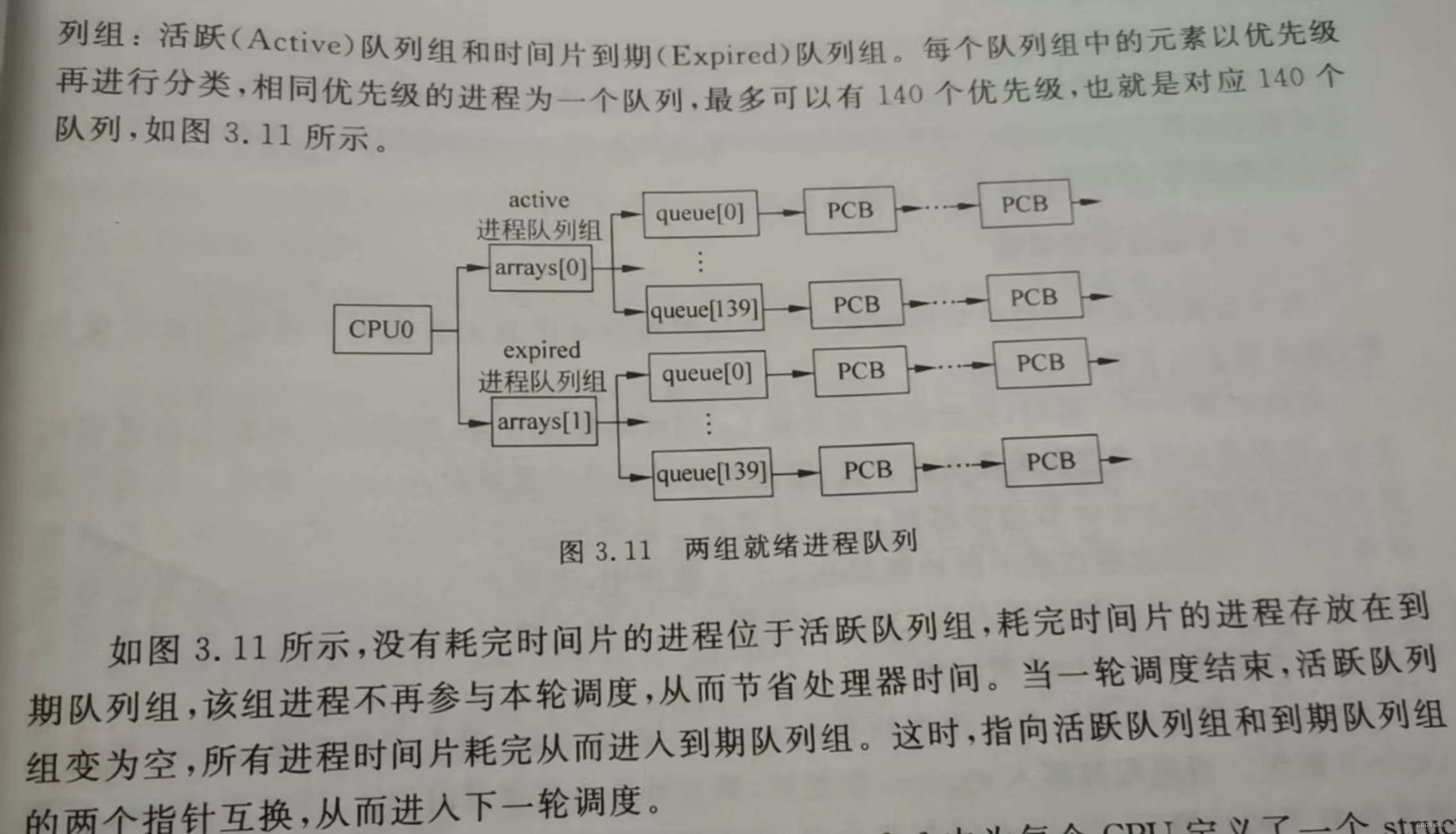
【linux温故】linux调度机制
假如你是设计者,你会设计怎样的调度机制呢? 时间片 最简单的,小学生都能想出来的一种,每个 ready task,按照一个固定的时间片轮流执行。 大家不要抢,挨个儿排队执行。执行完时间片,就排在后面…...

django中如何使用mysql连接池
一:介绍 在Django中使用MySQL时,通常情况下,Django的数据库层会为你管理数据库连接。Django的数据库接口是线程安全的,这意味着它会自动为每个线程创建和管理数据库连接。在大多数情况下,你不需要手动创建线程池来管理…...

3D高斯溅射:面向三维场景的实时渲染技术
1. 前言 高斯溅射技术【1】一经推出,立刻引起学术界和工业界的广泛关注。相比传统的隐式神经散射场渲染技术,高斯溅射依托椭球空间,显性地表示多目图像的三维空间关系,其计算效率和综合性能均有较大的提升,且更容易理…...
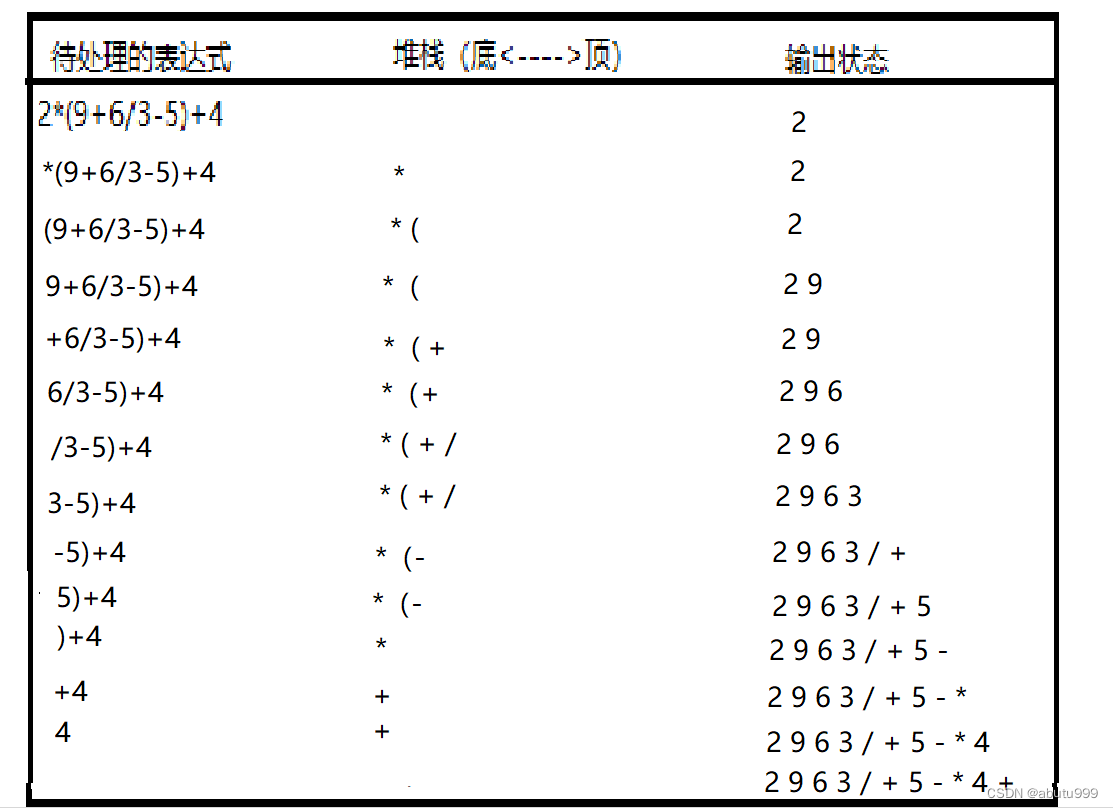
【数据结构】13:表达式转换(中缀表达式转成后缀表达式)
思想: 从头到尾依次读取中缀表达式里的每个对象,对不同对象按照不同的情况处理。 如果遇到空格,跳过如果遇到运算数字,直接输出如果遇到左括号,压栈如果遇到右括号,表示括号里的中缀表达式已经扫描完毕&a…...
-视图的创建和应用)
MySQL进阶查询篇(9)-视图的创建和应用
数据库视图是MySQL中一个非常重要的概念。它是一个虚拟表,由一个查询的结果集组成。数据库视图为用户提供了一种简化数据查询和操作的方式。本文将介绍MySQL数据库视图的创建和应用。 1. 创建数据库视图 要创建MySQL数据库视图,我们使用CREATE VIEW语句…...
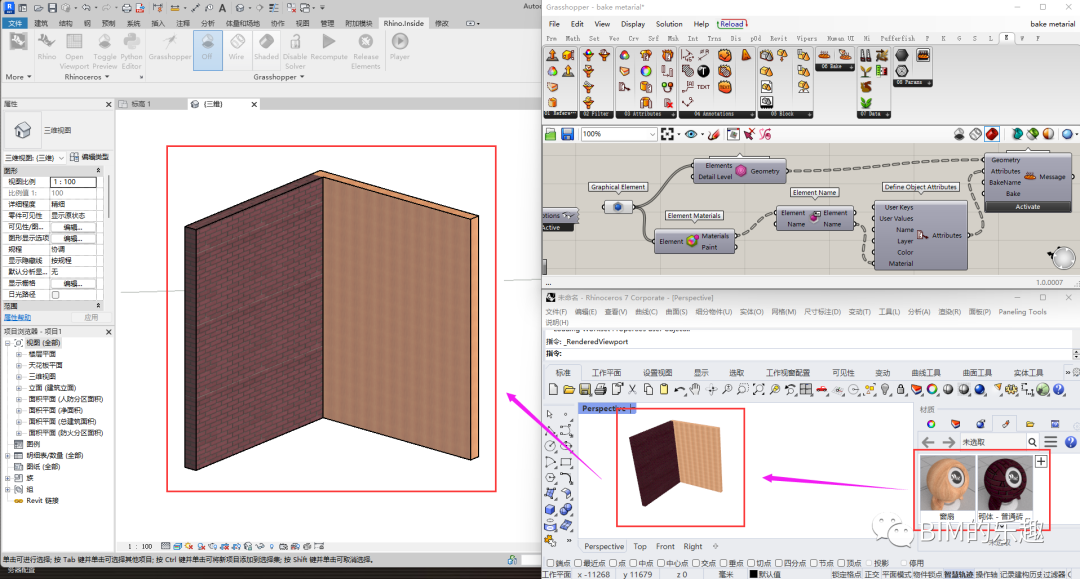
Rhino.Inside带材质将Revit模型bake到Rhino
Hello大家好!我是九哥~ 今天来讲一个小技巧,就是我通常采用RIR将Revit的模型的Geometry Bake到Rhino,肯定是没有材质的,那么如果我们需要带材质那要怎么办呢? 对于会的人,其实挺简单的,只需要…...

随记-Java项目处理SQL注入问题
现象:http://10.xx.xx.xx:xx/services/xxService 存在SQL注入情况 加固意见: 需要对网站所有参数中提交的数据进行过滤,禁止输入“"、"xor"、"or"、”--“、”#“、”select“、”and“等特殊字符;所有…...

精读《js 模块化发展》
1 引言 如今,Javascript 模块化规范非常方便、自然,但这个新规范仅执行了 2 年,就在 4 年前,js 的模块化还停留在运行时支持,10 年前,通过后端模版定义、注释定义模块依赖。对经历过来的人来说,…...
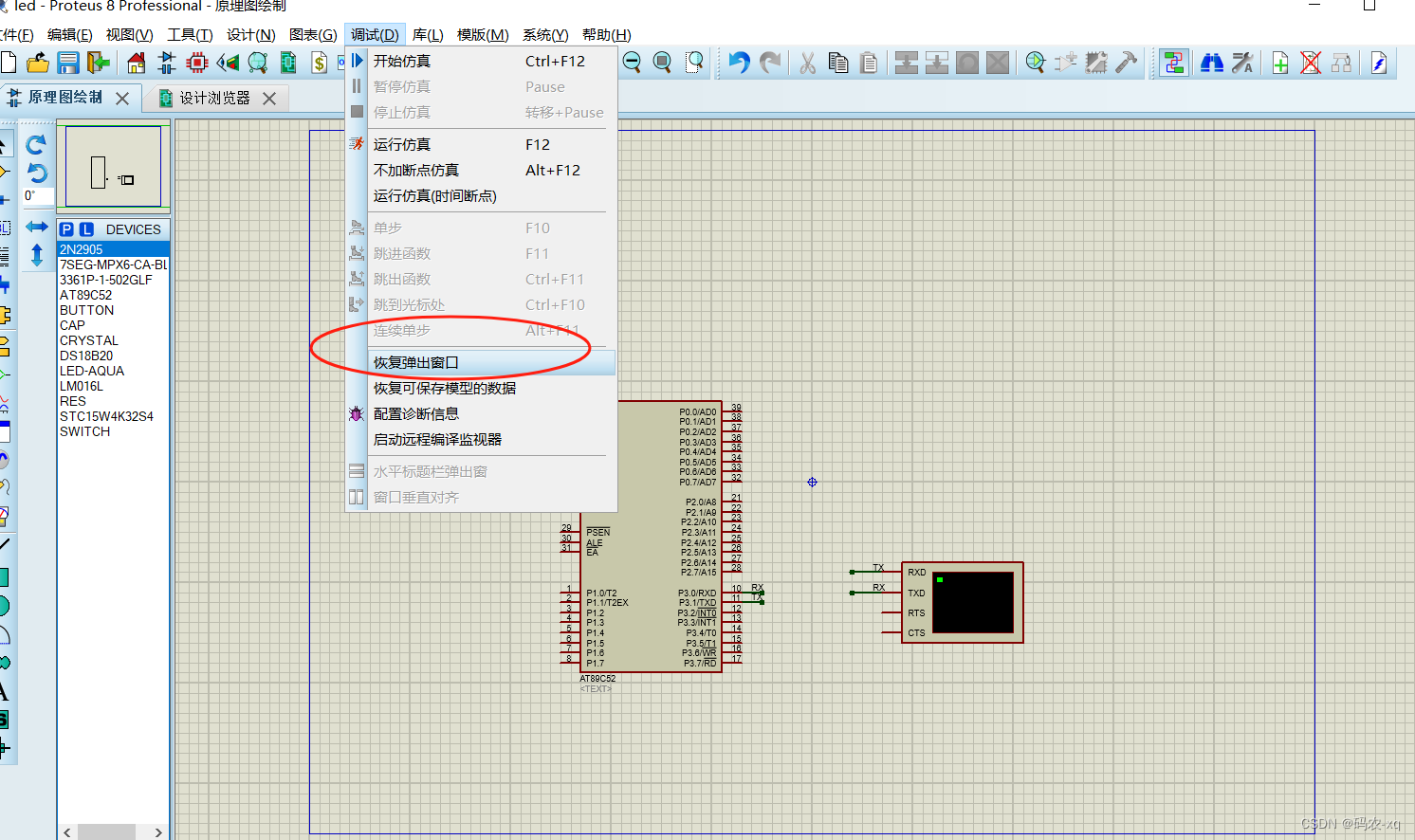
Proteus -模拟串口被关闭后怎样打开
Proteus -模拟串口被关闭后怎样打开 点击恢复弹出窗口,即可重新打开...

【深度学习】pytorch 与 PyG 安装(pip安装)
【深度学习】pytorch 与 PyG 安装(pip安装) 一、PyTorch安装和配置(一)、安装 CUDA(二)、安装torch、torchvision、torchaudio三个组件(1)下载镜像文件(2)创建…...

Bert与ChatGPT
1. Bert模型 BERT(Bidirectional Encoder Representations from Transformers)是一种预训练语言表示的方法,由Google AI在2018年提出。它标志着自然语言处理(NLP)领域的一个重大进步,因为它能够理解单词在…...
微信自动预约小程序开发指南:从小白到专家
随着互联网的发展,小程序已经成为了一个备受欢迎的在线预约平台。本文将详细介绍如何使用第三方制作平台,如乔拓云网,来搭建一个从入门到精通的预约小程序。 首先,我们需要登录乔拓云网,并选择一个适合自己的小程序模板…...
)
巴尔加瓦算法图解【完结】:算法运用(下)
目录 布隆过滤器HyperLogLogSHA算法比较文件检查密码 Diffie-Hellman密钥交换线性规划结语(完结) 布隆过滤器 在元素很多的情况下,判断一个元素是否在集合中可以使用布隆过滤器。布隆过滤器(Bloom Filter)是 1970 年由…...
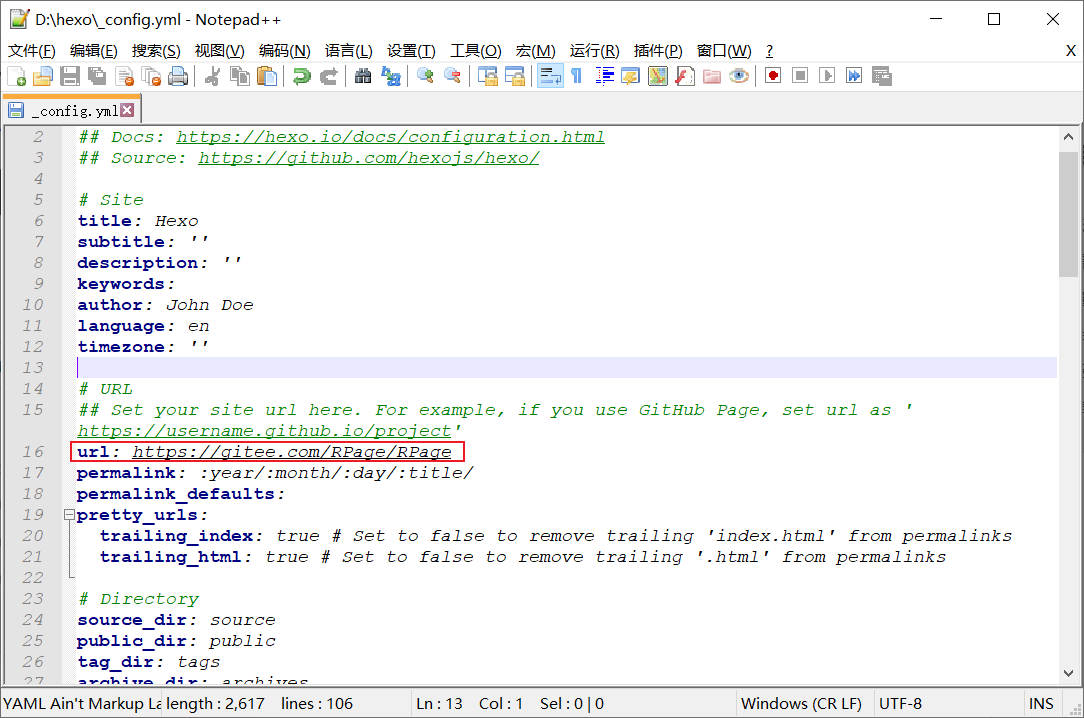
hexo部署到gitee(码云)
引言 Hexo 是一个基于Node.js的静态博客框架,而 Gitee(也被称为码云)是一个国内的代码托管平台,支持 Git 版本控制系统,与 GitHub 类似。将 Hexo 部署到 Gitee Pages 可以让你的博客受益于 Gitee 的国内服务器…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...
