Pytorch 复习总结 1
Pytorch 复习总结,仅供笔者使用,参考教材:
- 《动手学深度学习》
本文主要内容为:Pytorch 张量的常见运算、线性代数、高等数学、概率论。
Pytorch 张量的常见运算、线性代数、高等数学、概率论 部分 见 Pytorch 复习总结 1;
Pytorch 线性神经网络 部分 见 Pytorch 复习总结 2;
Pytorch 多层感知机 部分 见 Pytorch 复习总结 3;
Pytorch 深度学习计算 部分 见 Pytorch 复习总结 4;
Pytorch 卷积神经网络 部分 见 Pytorch 复习总结 5;
Pytorch 现代卷积神经网络 部分 见 Pytorch 复习总结 6;
目录
- 一. 数据操作
- 1. 张量的创建
- 2. 张量的基本操作
- 3. 按元素运算
- 4. 原地运算
- 5. 索引和切片
- 6. 数据类型转换
- 二. 数学运算
- 1. 线性代数
- 2. 高等数学
- 3. 概率论
一. 数据操作
张量 tensor 是 PyTorch 中的核心数据结构,类似于 Numpy 中的数组 ndarray。张量的本质是 n 维数组,可以很好地支持 GPU 加速计算,并且支持自动微分。使用张量需要导入头文件 torch,type 类型为 torch.Tensor。
1. 张量的创建
torch.arange(start=0, end, step=1):创建等差数列的行向量;import torch x = torch.arange(6) # tensor([0, 1, 2, 3, 4, 5]) y = torch.arange(1,6,2) # tensor([1, 3, 5])torch.zeros((a, b, ...))/torch.ones((a, b, ...))/torch.randn(a, b, ...)/torch.tensor([...]):创建元素全为 0 / 1 / 随机 / 指定的张量;import torch a = torch.zeros((2, 3, 4)) b = torch.ones((5)) c = torch.randn(3, 4) d = torch.tensor([[[2, 1], [4, 3]], [[1, 2], [3, 4]], [[4, 3], [2, 1]]])torch.zeros_like(x):创建与 x 形状相同的全零张量;import torch x = torch.tensor([[1, 2, 3], [4, 5, 6]]) y = torch.zeros_like(x) # tensor([[0, 0, 0], [0, 0, 0]])
张量中的数据类型可以通过 dtype 属性指定:
| 类型 | 说明 |
|---|---|
| torch.float64 | 双精度浮点数 |
| torch.float32 | 单精度浮点数 |
| torch.float16 | 半精度浮点数 |
| torch.int64 | 64 位有符号整数 |
| torch.int32 | 32 位有符号整数 |
| torch.int16 | 16 位有符号整数 |
| torch.int8 | 8 位有符号整数 |
| torch.uint8 | 8 位无符号整数 |
2. 张量的基本操作
x.shape/x.numel():返回张量的形状 / 元素总数;import torch x = torch.randn(3, 4) print(x.shape) # torch.Size([3, 4]) print(x.numel()) # 12x.reshape(a, b):改变原有张量的形状并返回新的张量,可以用 -1 自动计算某一维度的维数;import torch x = torch.arange(12) y = x.reshape(3, 4) print(y.shape) # torch.Size([3, 4]) z = x.reshape(2, 3, -1) print(z.shape) # torch.Size([2, 3, 2])torch.cat((a, b), dim=n):将张量沿第 i 个轴拼接;import torch a = torch.arange(12, dtype=torch.float32).reshape((3,4)) b = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]]) x = torch.cat((a, b), dim=0) # tensor([[ 0., 1., 2., 3.], [ 4., 5., 6., 7.], [ 8., 9., 10., 11.], [ 2., 1., 4., 3.], [ 1., 2., 3., 4.], [ 4., 3., 2., 1.]]) y = torch.cat((a, b), dim=1) # tensor([[ 0., 1., 2., 3., 2., 1., 4., 3.], [ 4., 5., 6., 7., 1., 2., 3., 4.], [ 8., 9., 10., 11., 4., 3., 2., 1.]])x.clone():张量的深拷贝(=这是浅拷贝,两个张量共享同一内存地址);
3. 按元素运算
+/-/*///**/%:按元素加 / 减 / 乘 / 除 / 幂 / 模;import torch x = torch.tensor([1.0, 2, 4, 8]) y = torch.tensor([2, 2, 2, 2]) a = x + y # tensor([ 3., 4., 6., 10.]) b = x - y # tensor([-1., 0., 2., 6.]) c = x * y # tensor([ 2., 4., 8., 16.]) d = x / y # tensor([0.5000, 1.0000, 2.0000, 4.0000]) e = x ** y # tensor([ 1., 4., 16., 64.]) f = x % y # tensor([1., 0., 0., 0.])torch.sin(x)/torch.cos(x)/torch.tan(x)/torch.sinh(x)/torch.cosh(x)/torch.tanh(x):按元素计算三角函数;torch.exp(x)/torch.log(x):按元素计算指数 / 对数函数;torch.logical_and(a, b))/torch.logical_or(a, b))/torch.logical_not(a):按元素逻辑与 / 或 / 非;>、<、=、torch.eq(a, b)/torch.gt(a, b)/torch.lt(a, b))/torch.ge(a, b)/torch.le(a, b):按元素比较;
上面按元素运算都是在相同形状的两个张量上执行的,如果两个形状不同的张量调用按元素运算操作,会按 广播机制 执行。广播机制会先适当复制元素将两个张量补全成相同形状,再按元素操作:
import torcha = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
print(a+b) # tensor([[0, 1], [1, 2], [2, 3]])
4. 原地运算
上一节介绍的运算都会为返回的张量分配新的内存,可以通过 id() 函数检查变量的内存地址:
import torchx = torch.tensor([1.0, 2, 4, 8])
y = torch.tensor([2, 2, 2, 2])
print(id(x)) # 2479607808944
x = x + y
print(id(x)) # 2479608211632
如果是在深度学习训练等场景中,参数会被不断更新,这样重复的操作会导致大量内存的无效占用。这时可以 执行原地操作,如 Z[:] = <expression> 或 X+=Y:
import torchx = torch.tensor([1, 2, 4, 8])
y = torch.tensor([1, 3, 5, 7])
z = torch.zeros_like(x)
print(id(x)) # 2049176339296
print(id(z)) # 2049176741984
z[:] = x + y
print(id(z)) # 2049176741984
x+=y
print(id(x)) # 2049176339296
5. 索引和切片
Pytorch 中的索引和切片和 Python 数组中操作一样:
import torchx = torch.arange(12).reshape((3,4))
print(x[-1]) # tensor([ 8, 9, 10, 11])
print(x[1:3]) # tensor([[ 4, 5, 6, 7], [ 8, 9, 10, 11]])
print(x[:, 1:3]) # tensor([[ 1, 2], [ 5, 6], [ 9, 10]])
x[2, 2] = 15
x[0:2, :] = 12
print(x) # tensor([[12, 12, 12, 12], [12, 12, 12, 12], [ 8, 9, 15, 11]])
6. 数据类型转换
张量可以通过 torch.tensor()、.numpy()、.tolist() 函数实现与 list、ndarray 的相互转化:
import numpy as np
import torchnumpy_array = np.array([[1, 2, 3], [4, 5, 6]])
tensor = torch.tensor([[7, 8, 9], [10, 11, 12]])
python_list = [[1, 2, 3], [4, 5, 6]]tensor_from_numpy = torch.tensor(numpy_array)
numpy_from_tensor = tensor.numpy()
tensor_from_list = torch.tensor(python_list)
list_from_tensor = tensor.tolist()
当张量 只含单个元素 时,还可以使用 .item() 函数将其转化为标量:
import torchx = torch.tensor([3])
n = x.item() # 3
二. 数学运算
1. 线性代数
A.T:矩阵转置,转置矩阵与原矩阵 共享内存空间;A*B:Hadamard 积,即形状相同的两个张量按元素乘,记为 A ⊙ B A \odot B A⊙B;torch.dot(x, y):列向量点积,记为 ⟨ x , y ⟩ \langle x, y\rangle ⟨x,y⟩ 或 x T y x^Ty xTy;torch.mv(A, x):矩阵-向量积,记为 A x Ax Ax;torch.mm(A, B):矩阵-矩阵积,记为 A B AB AB;torch.matmul(A, B):通用矩阵乘法,可以计算向量 / 矩阵的积;torch.abs(u).sum()/torch.norm(u):矩阵或向量的 L 1 L_1 L1 / L 2 L_2 L2 范数;import torch x = torch.tensor([3.0, -4.0]) y = torch.tensor([[1, 2], [2, 3], [3, 4]], dtype=torch.float32) print(torch.abs(x).sum()) # tensor(7.) print(torch.norm(x)) # tensor(5.) print(torch.abs(y).sum()) # tensor(15.) print(torch.norm(y)) # tensor(6.5574)
2. 高等数学
如果想要计算张量的梯度,在创建张量的时候需要 将 requires_grad 属性设置为 True。然后对张量的函数值调用 .backward() 方法计算张量的梯度(即偏导数),张量的梯度与原张量具有相同形状。.backward() 方法的可选属性如下:
gradient属性可以指定梯度的初始值,一般用于深度学习训练中梯度控制;retain_graph属性可以保留计算图以供后续的反向传播使用,以节省计算资源和时间。如果调用.backward()方法时不设置retain_graph=True,多次使用同一个计算图进行反向传播时就会出现 RuntimeError,因为计算图已经被释放;create_graph属性在可以指定计算梯度的同时创建计算图,以计算高阶导数时使用;
调用 .backward() 方法后,PyTorch 会自动 计算张量的梯度,并将梯度存储在张量的 .grad 属性中。如果想要继续计算高阶导数,需要清空 .grad 属性值:x.grad = None 或 x.grad.zero_()。
-
张量的一阶导数:
import torchx = torch.tensor(2.0, requires_grad=True) y = x**2 y.backward() print("Gradient of x:", x.grad.item()) # Gradient of x: 4.0 print("Type of x.grad:", type(x.grad)) # Type of x.grad: <class 'torch.Tensor'> -
张量的二阶导数:
import torchx = torch.tensor(2.0, requires_grad=True) y = x**3 y.backward(create_graph=True) # 计算一阶导数 first_derivative = x.grad.clone() # 获取一阶导数值 x.grad = None # 清空一阶导数值,以便存储二阶导数 first_derivative.backward() # 计算二阶导数 second_derivative = x.grad # 获取二阶导数值 print("Second derivative of x:", second_derivative.item()) # Second derivative of x: 12.0
然而,将 .backward() 函数的 create_graph 属性设置为 True 可能会导致内存泄漏。为了避免这种情况,创建计算图时经常使用 autograd.grad() 函数:
import torchx = torch.tensor(2.0, requires_grad=True)
y = x**4
first_derivative = torch.autograd.grad(y, x, create_graph=True)[0] # 计算一阶导数
second_derivative = torch.autograd.grad(first_derivative, x)[0] # 计算二阶导数
print("First derivative of x:", first_derivative.item()) # First derivative of x: 32.0
print("Second derivative of x:", second_derivative.item()) # Second derivative of x: 48.0
需要注意的是,求导的目标函数必须是标量,否则无法隐式创建梯度。
3. 概率论
-
聚合函数:使用
torch.sum(x)/torch.mean(x)/torch.max(x)/torch.min(x)/torch.std(x)/torch.var(x)计算张量元素的和 / 均值 / 最大值 / 最小值 / 标准差 / 方差,用法同x.sum()/x.mean()/x.max()/x.min()/x.std()/x.var()。聚合函数可以通过axis指定聚合的维度:import torch x = torch.tensor([[[1, 2], [2, 3], [3, 4]], [[4, 5], [5, 6], [6, 7]]], dtype=torch.float32) a = x.sum() # tensor(48.) b = x.sum(axis=0) # tensor([[ 5., 7.], [ 7., 9.], [ 9., 11.]]) c = x.sum(axis=1) # tensor([[ 6., 9.], [15., 18.]]) d = x.sum(axis=2) # tensor([[ 3., 5., 7.], [ 9., 11., 13.]]) e = x.sum(axis=[0, 1]) # tensor([21., 27.])还可以通过
keepdims属性保持轴数不变:import torch x = torch.tensor([[[1, 2], [2, 3], [3, 4]], [[4, 5], [5, 6], [6, 7]]], dtype=torch.float32) a = x.sum(axis=1, keepdims=True) print(a) ''' tensor([[[ 6., 9.]],[[15., 18.]]]) ''' -
采样函数:可以使用
.sample()函数对torch.distributions模块中的各种概率分布对象进行采样,常见分布如下:torch.distributions.Categorical:分类分布,是一种离散型随机变量分布,用于描述随机变量取每个类别值的概率;import torch import torch.distributions as dist probs = torch.tensor([0.2, 0.3, 0.5]) categorical_dist = dist.Categorical(probs) sample = categorical_dist.sample((20,))torch.distributions.Bernoulli:伯努利分布,也叫两点分布,是一种离散型随机变量分布,用于描述二值变量取每个值的概率;import torch.distributions as dist p = 0.6 bernoulli_dist = dist.Bernoulli(p) sample = bernoulli_dist.sample((20,))torch.distributions.Multinomial:多项式分布,是一种离散型随机变量分布,是二项分布的一般形式;import torch import torch.distributions as dist n = 10 probs = torch.tensor([0.1, 0.2, 0.7]) multinomial_dist = dist.Multinomial(n, probs) sample = multinomial_dist.sample()torch.distributions.Poisson:泊松分布,是一种离散型随机变量分布,用于描述随机变量在固定间隔中发生次数的概率;import torch.distributions as dist lam = 3 poisson_dist = dist.Poisson(lam) sample = poisson_dist.sample((20,))torch.distributions.Uniform:均匀分布,是一种连续型随机变量分布,用于描述随机变量在连续区间上均匀取值的情况;import torch.distributions as dist a, b = 3, 5 uniform_dist = dist.Uniform(a, b) sample = uniform_dist.sample((5,))torch.distributions.Exponential:指数分布,是一种连续型随机变量分布,是 Gamma 分布形状参数为 1 时的特例;import torch.distributions as dist lam = 3 exponential_dist = dist.Exponential(lam) sample = exponential_dist.sample((20,))torch.distributions.Normal:正态分布,是一种连续型随机变量分布,是最常见最一般的分布;import torch.distributions as dist mu = 0 sigma = 1 normal_dist = dist.Normal(mu, sigma) sample = normal_dist.sample((20,5))torch.distributions.Gamma:Gamma 分布,是一种连续型随机变量分布,用于描述某一事件发生的等待时间;import torch.distributions as dist gamma_dist = dist.Gamma(2, 1) sample = gamma_dist.sample((20,))torch.distributions.Beta:Beta 分布,是一种连续型随机变量分布,用于描述随机变量在有界区间 [0, 1] 上的取值情况;import torch.distributions as dist alpha, beta = 2, 5 beta_dist = dist.Beta(alpha, beta) sample = beta_dist.sample((5,))
.sample()函数内可以加入采样张量的维度,为空则默认只采样一次,如果是一维张量,需要在维度后加上逗号,如:.sample((20,))。
想要查找模块中更多的函数和类,可以调用 dir() 函数:
import torch
print(dir(torch.distributions))
想要查找特定函数和类的用法,可以调用 help() 函数:
import torch
help(torch.ones)
相关文章:

Pytorch 复习总结 1
Pytorch 复习总结,仅供笔者使用,参考教材: 《动手学深度学习》 本文主要内容为:Pytorch 张量的常见运算、线性代数、高等数学、概率论。 Pytorch 张量的常见运算、线性代数、高等数学、概率论 部分 见 Pytorch 复习总结 1&…...
)
谷歌免费开放模糊测试框架OSS-Fuzz(物联网、车联网、供应链安全、C/C++)
目录 模糊测试的智能化和自动化 模糊测试不能代替安全设计原则 AI驱动的漏洞修补...
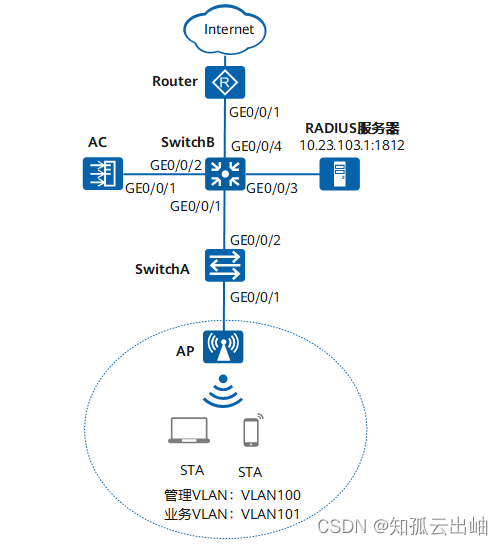
华为配置内部人员接入WLAN网络示例(802.1X认证)
配置内部人员接入WLAN网络示例(802.1X认证) 组网图形 图1 配置802.1X认证组网图 业务需求组网需求数据规划配置思路配置注意事项操作步骤配置文件 业务需求 用户接入WLAN网络,使用802.1X客户端进行认证,输入正确的用户名和密…...
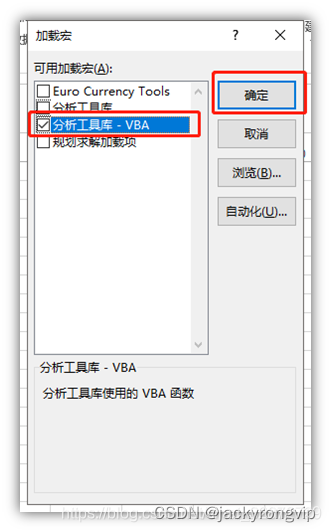
EXCEL中如何调出“数据分析”的菜单
今天发现,原来WPS还是和EXCEL比,还是少了“数据分析”这个日常基本做统计的菜单,只好用EXCEL了,但奇怪发现我的EXCEL中没发现这个菜单,然后查了下,才发现,要用如下的方法打开: 1&…...
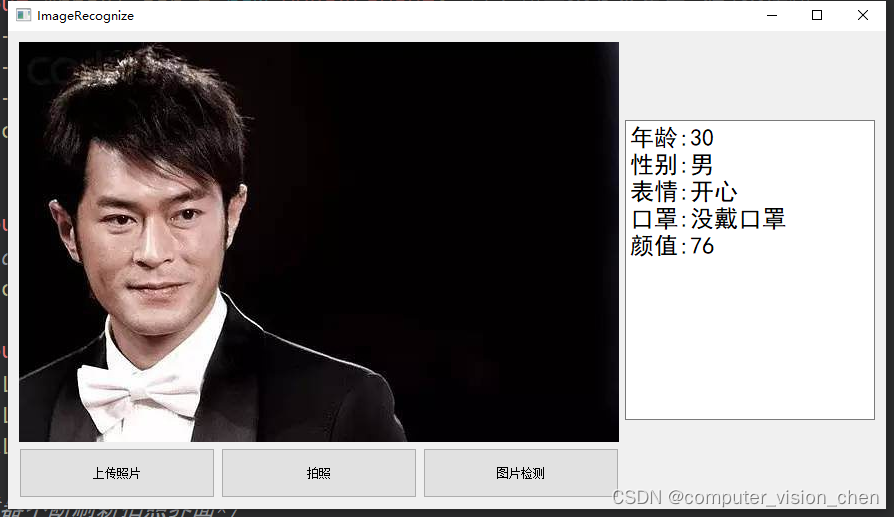
基于Qt的人脸识别项目(功能:颜值检测,口罩检测,表情检测,性别检测,年龄预测等)
完整代码链接在文章末尾 效果展示 代码讲解(待更新) qt图片文件上传 #include <QtWidgets> #include <QFileDialog>...

书生谱语-大语言模型测试demo
课程内容简介 通用环境配置 开发机 InterStudio 配置公钥 在本地机器上打开 Power Shell 终端。在终端中,运行以下命令来生成 SSH 密钥对: ssh-keygen -t rsa您将被提示选择密钥文件的保存位置,默认情况下是在 ~/.ssh/ 目录中。按 Enter …...
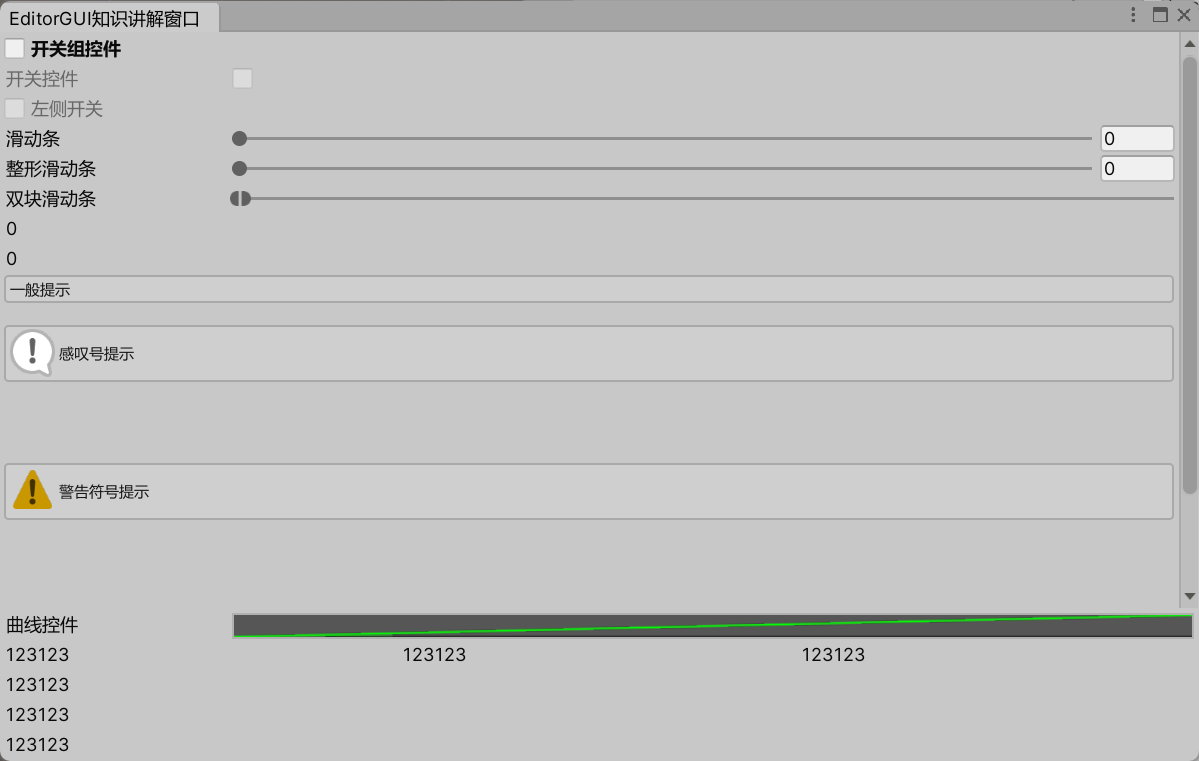
2024-02-12 Unity 编辑器开发之编辑器拓展3 —— EditorGUI
文章目录 1 GUILayout2 EditorGUI 介绍3 文本、层级、标签、颜色拾取3.1 LabelField3.2 LayerField3.3 TagField3.4 ColorField3.5 代码示例 4 枚举选择、整数选择、按下按钮4.1 EnumPopup / EnumFlagsField4.2 IntPopup4.3 DropdownButton4.4 代码示例 5 对象关联、各类型输入…...

shell脚本编译与解析
文章目录 shell变量全局变量(环境变量)局部变量设置PATH 环境变量修改变量属性 启动文件环境变量持久化 ./和. 的区别脚本编写判断 和循环命令行参数传入参数循环读取命令行参数获取用户输入 处理选项处理简单选项处理带值选项 重定向显示并且同时输出到…...

第64讲个人中心用户操作菜单实现
静态页面 <!-- 用户操作菜单开始 --><view class"user_menu"><!-- 订单管理开始 --><view class"order_wrap"><view class"order_title">我的订单</view><view class"order_content"><n…...
线性代数的本质——1 向量
向量是线性代数中最为基础的概念。 何为向量? 从物理上看, 向量就是既有大小又有方向的量,只要这两者一定,就可以在空间中随便移动。 从计算机应用的角度看,向量和列表很接近,可以用来描述某对象的几个不同…...

工业以太网交换机引领现代工厂自动化新潮流
随着科技的飞速发展,现代工厂正迎来一场前所未有的自动化变革,而工业以太网交换机的崭新角色正是这场变革的关键组成部分。本文将深入探讨工业以太网交换机与现代工厂自动化的紧密集成,探讨这一集成如何推动工业生产的智能化、效率提升以及未…...
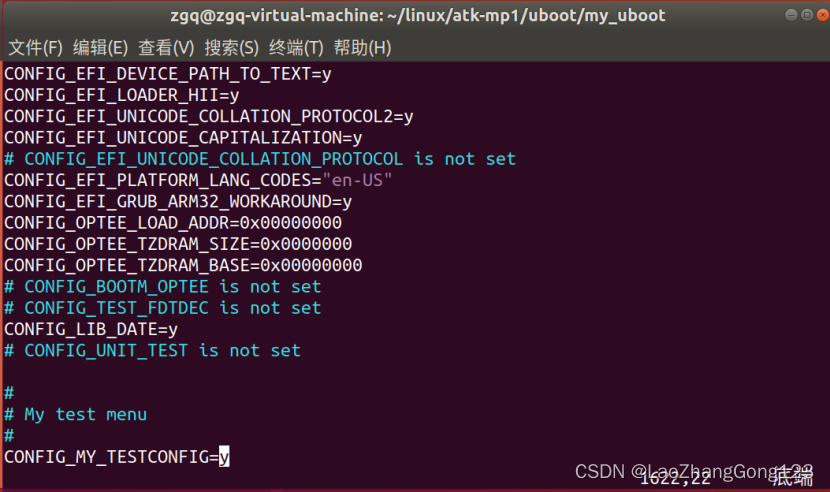
Linux第46步_通过“添加自定义菜单”来学习menuconfig图形化配置原理
通过“添加自定义菜单”来学习menuconfig图形化配置原理,将来移植linux要用到。 自定义菜单要求如下: ①、在主界面中添加一个名为“My test menu”,此菜单内部有一个配置项。 ②、配置项为“MY TESTCONFIG”,此配置项处于菜单“My test m…...
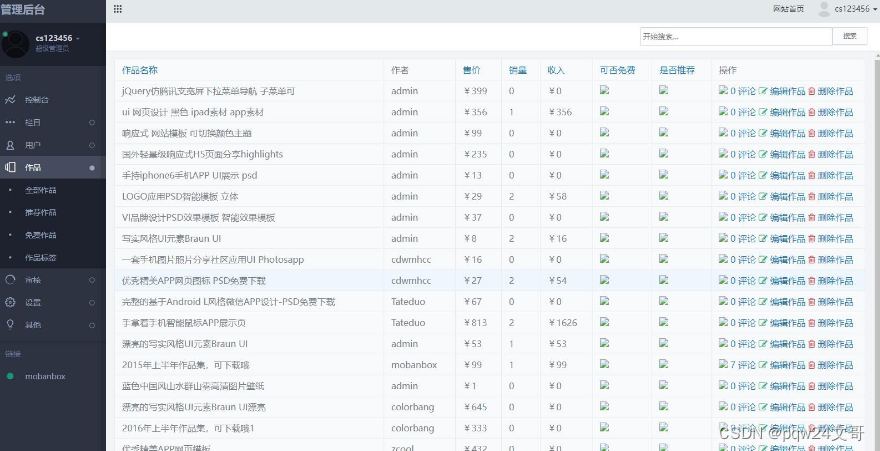
推荐高端资源素材图库下载平台整站源码
推荐高端图库素材下载站的响应式模板和完整的整站源码,适用于娱乐网资源网。该模板支持移动端,并集成了支付宝接口。 演示地 址 : runruncode.com/tupiao/19692.html 页面设计精美,不亚于大型网站的美工水准,并且用户…...

Redis实现:每个进程每30秒执行一次任务
前言 项目中要实现每一进程每30秒执行一次 代码实现: public class DistributedScheduler {private final RRedisClient redisson;private final String processKeyPrefix; // 例如 "process_"public DistributedScheduler(RRedisClient redisson) {this.redisson…...

【AI之路】使用RWKV-Runner启动大模型,彻底实现大模型自由
文章目录 前言一、RWKV-Runner是什么?RWKV-Runner是一个大语言模型的启动平台RWKV-Runner官方功能介绍 二、使用步骤1. 下载文件 总结 前言 提示:这里可以添加本文要记录的大概内容: ChatGPT的横空出世,打开了AI的大门ÿ…...

Dockerfile和.gitlab-ci.yml文件模板
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...
Linux--基础开发工具篇(2)(vim)(配置白名单sudo)
目录 前言 1. vim 1.1vim的基本概念 1.2vim的基本操作 1.3vim命令模式命令集 1.4vim底行命令 1.5 异常问题 1.6 批量注释和批量去注释 1.7解决普通用户无法sudo的问题 1.8简单vim配置 前言 在前面我们学习了yum,也就是Linux系统的应用商店 Linux--基础开…...

Learn LaTeX 017 - LaTex Multicolumn 分栏
在科学排版中进行分栏操作,能够有效的利用页面中的空间,避免空白位置的浪费。 好的分栏设计能对你的排版增色不少! https://www.ixigua.com/7298100920137548288?id7307237715659981346&logTag949adb699806392430bb...

Android 9.0 禁用adb install 安装app功能
1.前言 在9.0的系统产品定制化开发中,在进行一些定制开发中,对于一些app需要通过属性来控制禁止安装,比如adb install也不允许安装,所以就需要 熟悉adb install的安装流程,然后来禁用adb install安装功能,接下来分析下adb 下的安装流程 2.禁用adb install 安装app功能的…...
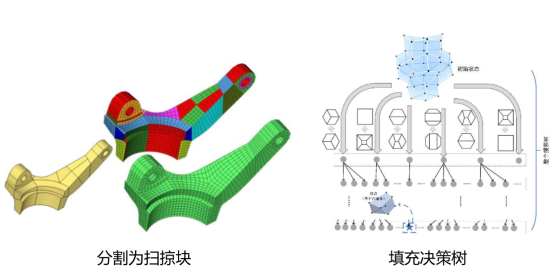
华为第二批难题五:AI技术提升六面体网格生成自动化问题
有CAE开发商问及OCCT几何内核的网格方面的技术问题。其实,OCCT几何内核的现有网格生成能力比较弱。 HybridOctree_Hex的源代码,还没有仔细去学习。 “HybridOctree_Hex”的开发者说:六面体网格主要是用在数值模拟领域的,比如汽车…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...
