用Python动态展示排序算法
文章目录
- 选择冒泡
- 插入排序
- 归并排序
- 希尔排序
经常看到这种算法可视化的图片,但往往做不到和画图的人心灵相通,所以想自己画一下,本文主要实现归并排序和希尔排序,如果想实现其他算法可参考这篇
C语言实现各种排序算法[选择,冒泡,插入,归并,希尔,快排,堆排序,计数]
选择冒泡
这两种排序方案简单到很难说是什么算法,其中选择排序通过遍历一次数组,选出其中最大(小)的值放在新数组的第一位,再从剩下的数里选出最大(小)的,放到第二位,依次类推;冒泡排序则是通过重复走访要排序的数组,比较相邻元素,如果顺序不符合要求则交换位置,直到不需要交换为止。
| 选择排序 | 冒泡排序 |
|---|---|
 |  |
二者的核心代码分别为:
#x为待排序列表,N=len(x)
#选择排序
for i in range(N):iMax = ifor j in range(i, N):if(x[j]>x[iMax]):iMax = jx[iMax],x[i] = x[i],x[iMax]#冒泡排序
tempN = N-1
for i in range(tempN):for j in range(0, tempN-i):if(x[j]>x[j+1]):x[j],x[j+1] = x[j+1],x[j]
下面给出选择排序的绘图代码,其他的所有排序算法,其实只需改变核心部分。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation start,end,N = 10,100,9
x = np.random.randint(start, end, size=N)
Index = np.arange(N)
xs = []
nowIndex = []for i in range(N):iMax = ifor j in range(i, N):xs.append(x*1) #存储当前顺序,用于绘图nowIndex.append([i,j,iMax]) #存储当前的i,j,max位置,用于绘图if(x[j]>x[iMax]):iMax = jxs.append(x*1)nowIndex.append([i,j,iMax])x[iMax],x[i] = x[i],x[iMax]fig, ax = plt.subplots()
colors = np.repeat('g',N)
colors[0] = 'b'
bar = ax.bar(Index,x,color=colors)def animate(n):data = xs[n]colors = np.repeat('gray',N)colors[nowIndex[n]] = 'b','g','r'ax.clear()bar = ax.bar(Index, data, color=colors)return barani = animation.FuncAnimation(fig, animate, range(len(xs)), interval=500, repeat=False, blit=True)
plt.show()
ani.save("sort.gif")
插入排序
插入排序的基本思路是将数组分为前后两个部分,前面有序,后面无序。逐个扫描无序数组,将每次扫描的数插入到有序数组中,从而有序数组越来越长,无序数组越来越短,直到整个数组都是有序的。
核心代码为
for i in range(1,N):j = i-1temp = x[i]while(x[i]<x[j] and j>=0):x[j+1] = x[j]j -= 1x[j+1] = temp
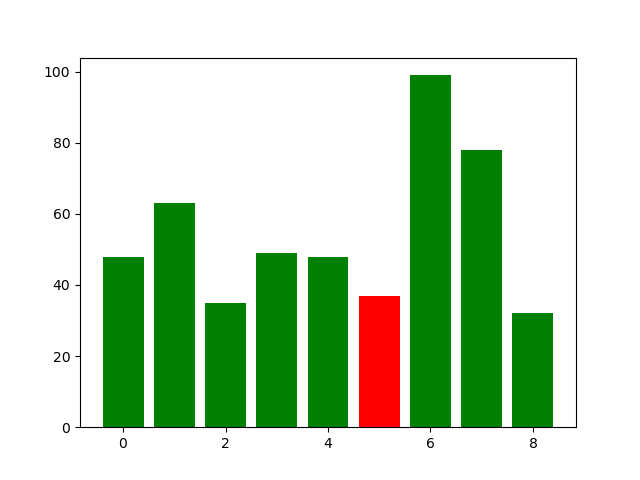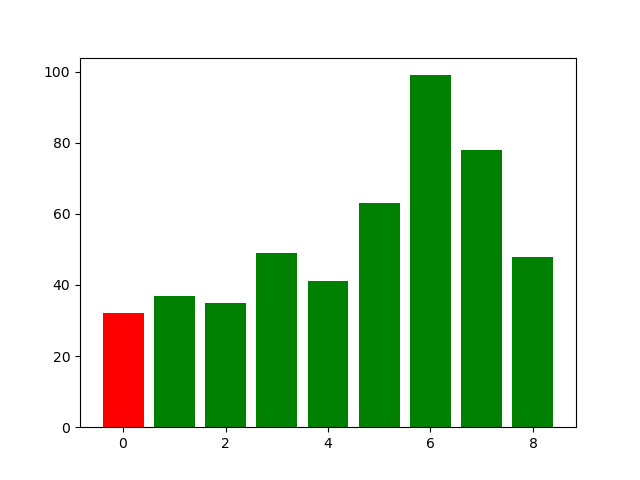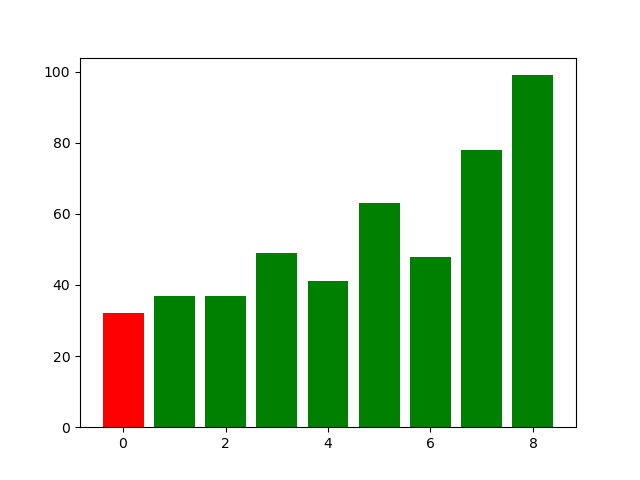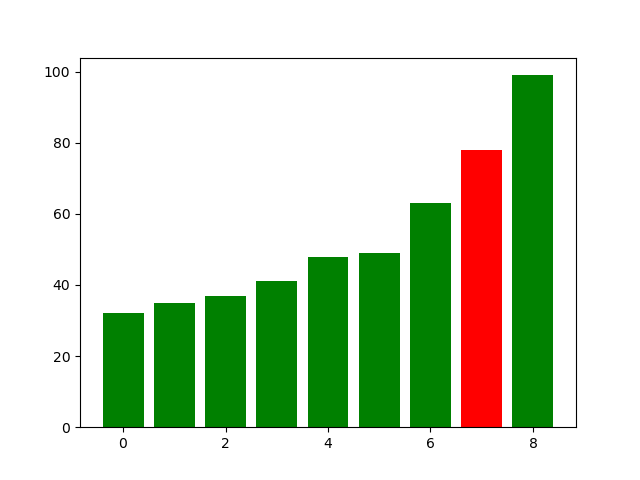
由于在这段代码中, x i x_i xi被取出放在旁边,所以其动态图中大部分时间会缺失一个值,在图中将其置于最右侧,其动态过程如图所示,蓝色表示抽出来准备插进去的那根bar

归并排序
排序算法到这里才算有点意思,归并排序是算法导论中介绍分治概念时提到的,基本思路是将数组拆分成子数组,然后令子数组有序,再令数组之间有序,从而整个数组有序。
算法步骤 \textbf{算法步骤} 算法步骤
设数组有 n n n个元素, { a 0 , a 1 , … , a n } \{a_0,a_1,\ldots,a_n\} {a0,a1,…,an}
- 如果数组元素大于2,则将数组分成左数组和右数组,如果数组等于2,则将数组转成有序数组
- 对左数组和右数组执行1操作。
- 合并左数组和右数组。
可以发现,对长度为 n n n的数组,需要 log 2 n \log_2n log2n次的拆分,每个拆分层级都有 O ( n ) O(n) O(n)的时间复杂度和 O ( n ) O(n) O(n)的空间复杂度,所以其时间复杂度和空间复杂度分别为 O ( n log 2 n ) 和 O ( n ) O(n\log_2n)和O(n) O(nlog2n)和O(n)。
其核心算法为
def Merge(X, Y):nL,nR = len(X), len(Y)iterL,iterR = 0,0xNew = []for _ in range(nL+nR):if(iterL==nL): return xNew + Y[iterR:]if(iterR==nR): return xNew + X[iterL:]if(X[iterL]<Y[iterR]):xNew.append(X[iterL])iterL += 1else:xNew.append(Y[iterR])iterR += 1return xNewdef MergeSort(x):if len(x)==1:return xif len(x)==2:return x if x[0]<x[1] else [x[1],x[0]]nL = len(x)//2return Merge(MergeSort(x[:nL]),MergeSort(x[nL:]))
当然这么写效率是非常低的,如果像高效还是得用指针,但我都已经用Python了,所以就不去想效率的问题,问题的关键是这种带有返回值的递归程序根本没法画图啊。。。所以还是改成指针的写法
def Merge(X, nL):nR = len(X)-nLXL,XR = X[:nL]*1,X[nL:]*1iterL,iterR = 0,0for i in range(nL+nR):if(iterL==nL): breakif(iterR==nR): X[i:] = XL[iterL:]returnif(XL[iterL]<XR[iterR]):X[i] = XL[iterL]iterL += 1else:X[i] = XR[iterR]iterR += 1def MergeSort(X):if len(X)<2:returnnL = len(X)//2MergeSort(X[:nL])MergeSort(X[nL:])Merge(X,nL)
这个图。。怎么说呢,因为在【Merge】过程中,有很多bar被掩盖掉了,所以可能只有画图的人能看懂吧。。。

希尔排序
据说是第一个突破 O ( n 2 ) O(n^2) O(n2)的排序算法,又称为缩小增量排序,本质上也是一种分治方案。
在归并排序中,先将长度为n的数组划分为nL和nR两部分,然后继续划分,直到每个数组的长度不大于2,再对每个不大于2的数组进行排序。这样,每个子数组内部有序而整体无序,然后将有序的数组进行回溯重组,直到重新变成长度为n的数组为止。
希尔排序反其道而行之,在将数组划分为nL和nR后,对nL和nR进行按位排序,使得nL和nR内部无序,但整体有序。然后再将数组进行细分,当数组长度变成1的时候,内部也就谈不上无序了,而所有长度为1的数组整体有序,也就是说有这些子数组所组成的数组是有序的。
算法步骤 \textbf{算法步骤} 算法步骤
设数组有 n n n个元素, { a 0 , a 1 , … , a n } \{a_0,a_1,\ldots,a_n\} {a0,a1,…,an}
- 如果数组元素大于2,则将数组分成左数组和右数组,并对左数组和右数组的元素进行一对一地排序。
- 对每一个数组进行细分,然后将每个子数组进行一对一排序。
def ShellSort(arr):n = len(arr)nSub = n//2while nSub>0:for i in range(nSub,n):temp = arr[i]j = i-nSubwhile j>=0 and temp<arr[j]:arr[j+nSub] = arr[j]j -= nSubarr[j+nSub] = tempnSub //= 2
相关文章:

用Python动态展示排序算法
文章目录 选择冒泡插入排序归并排序希尔排序 经常看到这种算法可视化的图片,但往往做不到和画图的人心灵相通,所以想自己画一下,本文主要实现归并排序和希尔排序,如果想实现其他算法可参考这篇 C语言实现各种排序算法[选择&#x…...

vscode代码快捷键
1、 log console.log()2、edf export default (first)>{ second } 或者 export default function(params)>{ }可以使用tab键切换修改项 3、ednf export default function first(second) {third}4、! 生成html模板 5、div#app <div id"app"></di…...

深入了解C++:形参、内联、重载、引用、const和指针、new和delete
形参带默认值的函数 1.给默认值的时候从右向左给。 2.定义出可以给形参默认值,声明也可以给形参默认值。 3.形参默认值只能出现一次。 4.参数调用的效率问题 #sum(10,20)对应了五条汇编指令 mov eax,dword ptr[ebp-8] push eax mov ecx dword ptr[ebp-4] push …...

Linux 目录结构结构
Linux 目录结构结构 概念 Linux 没有 C、D、E...盘符,只有一个目录树。通过挂载,将不同的磁盘挂载到目录树下,通过目录访问磁盘。 不同目录的作用 目录存放内容/作用/根目录,目录树的起点,存放所有文件。…...
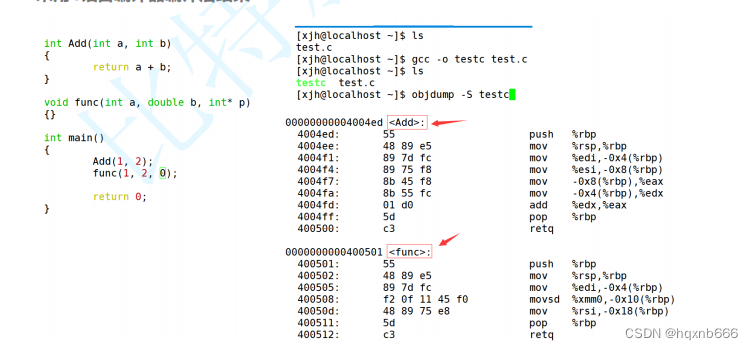
C++基础入门:掌握核心概念(超全!)
C作为一门广泛使用的编程语言,以其高性能和灵活性在软件开发领域占据重要地位。无论是游戏开发、系统编程还是实时应用,C都是一个不可或缺的工具。本博客旨在为初学者提供C编程语言的核心概念,帮助你建立坚实的基础。 C关键字 C关键字是编程…...
Linux第47步_安装支持linux的第三方库和mkimage工具
安装支持linux的第三方库和mkimage工具,做好移植前的准备工作。 编译linux内核之前,需要先在 ubuntu上安装“lzop库”和“libssl-dev库”,否则内核编译会失败。 mkimage工具会在zImage镜像文件的前面添加0x40个字节的头部信息,就可以得到uI…...
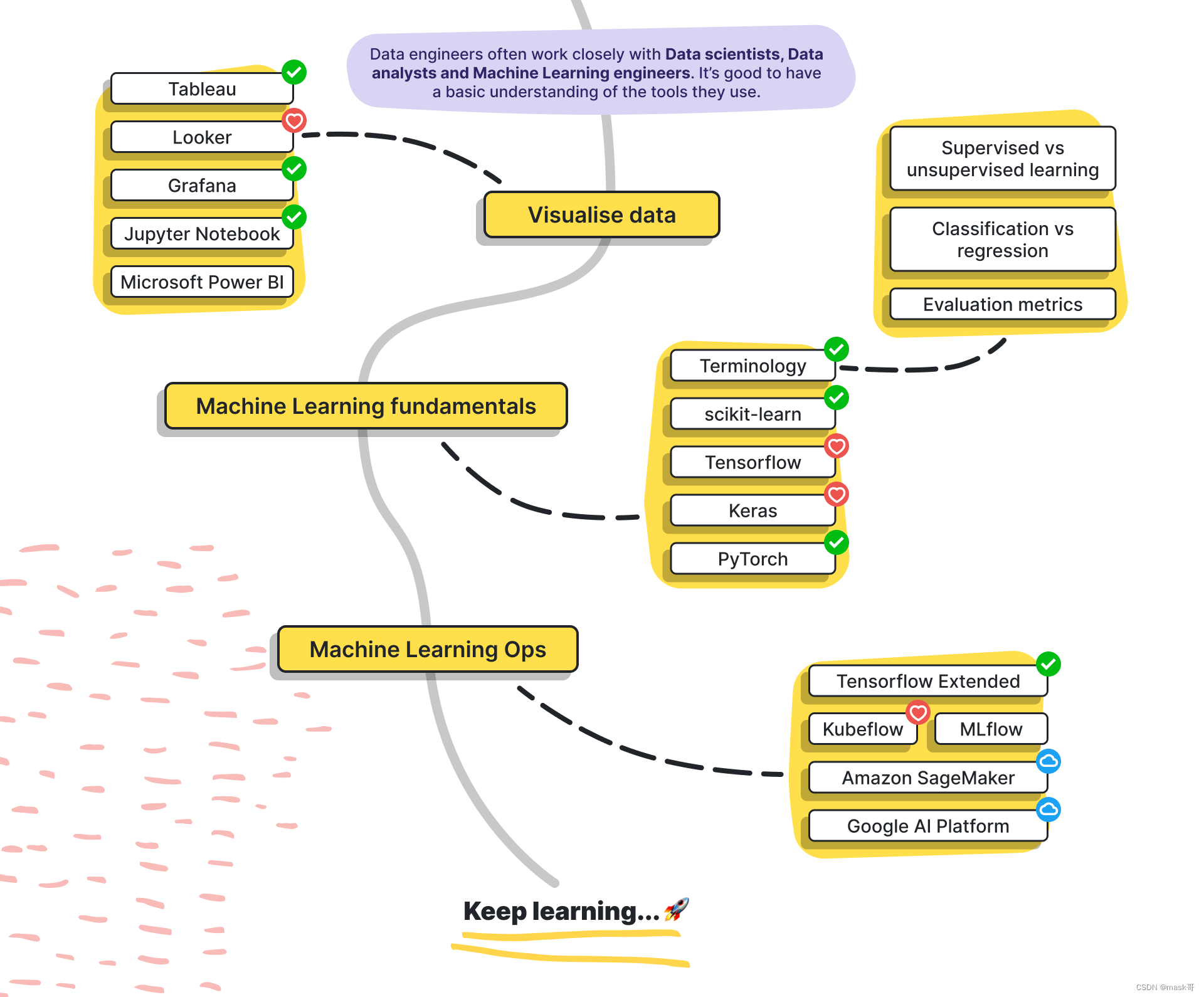
数据工程工程师学习路线图
数据工程岗位要求 Skill Sets required: - Hands on experience enabling data via Adobe Analytics and/or Google Analytics - Understanding of how customer level data is captured and stitched with behavioural data - Experience working with Testing (QA) and D…...

MySQL主从同步与分库分表
分库分表...

百度PaddleOCR字符识别推理部署(C++)
1 环境 1.opencv(https://sourceforge.net/projects/opencvlibrary/) 2.cmake(https://cmake.org/download/) 3.vs2019((https://github.com/PaddlePaddle/PaddleOCR/tree/release/2.1) 4.paddleOCR项目-建议2.0(http…...

C++ Qt框架开发 | 基于Qt框架开发实时成绩显示排序系统(2)折线图显示
对上一篇的工作C学习笔记 | 基于Qt框架开发实时成绩显示排序系统1-CSDN博客继续优化,增加一个显示运动员每组成绩的折线图。 1)在Qt Creator的项目文件(.pro文件)中添加对Qt Charts模块的支持: QT charts 2…...
Microsoft Excel 加载数据分析工具
Microsoft Excel 加载数据分析工具 1. 打开 Excel,文件 -> 选项2. 加载项 -> 转到…3. 分析工具库、分析工具库 - VBA4. 打开 Excel,数据 -> 数据分析References 1. 打开 Excel,文件 -> 选项 2. 加载项 -> 转到… 3…...

Day32 贪心算法part02
买卖股票的最佳时机 太牛了我,随随便便双指针秒杀 md题解里面双指针都没用直接for循环秒杀 跳跃游戏 写成这样纯粹是没有看到第一次跳跃必须从第一个开始 class Solution:def canJump(self, nums: List[int]) -> bool:if len(nums) 1:return Truefor i in …...
)
3分钟带你了解Vue3的nextTick()
前言 Vue 实现响应式并不是数据发生变化之后 DOM 立即变化,而是按一定的策略进行 DOM 的更新。简单来说,Vue在修改数据后,视图不会立刻更新,而是等同一事件循环中的所有数据变化完成之后,再统一进行视图更新ÿ…...

数据库的使用方法
sqlite3 API: 头文件: #include <sqlite3.h> 编译时候要加上-lsqlite3 gcc a.c -lsqlite3 1)sqlite3_open int sqlite3_open(const char *filename, /* Database filename (UTF-8) */ sqlite3 **ppDb /* OUT: SQLite db …...

HTML5和CSS3强化知识总结
HTML5的新特性 HTML5的新增特性主要是针对于以前的不足,增一些新的标签、新的表单和新的表单属性等。这些新特性都有兼容性问题,基本是IE9以上版本的浏览器才支持,如果不考虑兼容性问题,可以大量使用这些新特性。 HTML5新增的语义…...
华为机考入门python3--(13)牛客13-句子逆序
分类:列表 知识点: 列表逆序(和字符串逆序是一样的) my_list[::-1] 题目来自【牛客】 def reverse_sentence(sentence): # 将输入的句子分割words sentence.split() # 将单词逆序排列 words words[::-1] # 将单词用空…...
文件上传、断点续传、断网重传)
javaScript实现客户端直连AWS S3(亚马逊云)文件上传、断点续传、断网重传
写在前面:在做这个调研时我遇到的需求是前端直接对接亚马逊平台实现文件上传功能。上传视频文件通常十几个G、客户工作环境网络较差KB/s,且保证上传是稳定的,支持网络异常断点重试、文件断开支持二次拖入自动重传等。综合考虑使用的Aws S3的分…...
从基建发力,CESS 如何推动 RWA 发展?
2023 年 11 月 30 日,Web3 基金会(Web3 Foundation)宣布通过 Centrifuge 将部分资金投资于 RWA(Real World Assets,真实世界资产),试点投资为 100 万美元。Web3 基金会旨在通过支持专注于隐私、…...
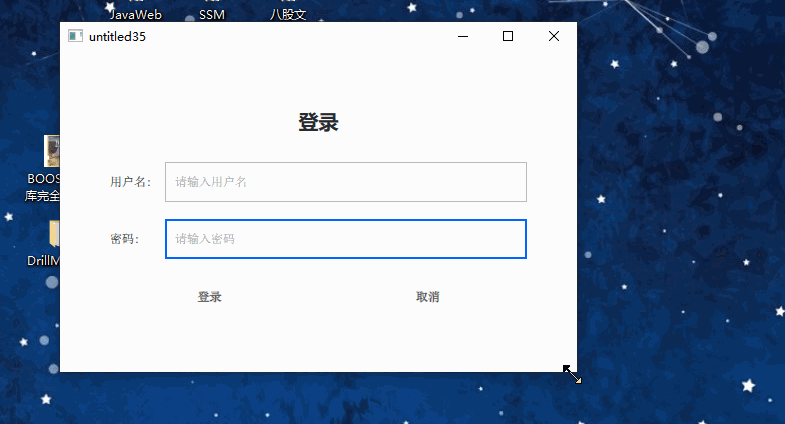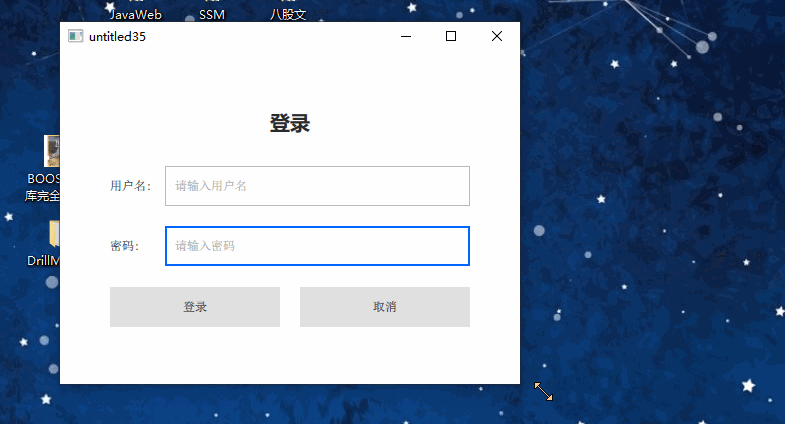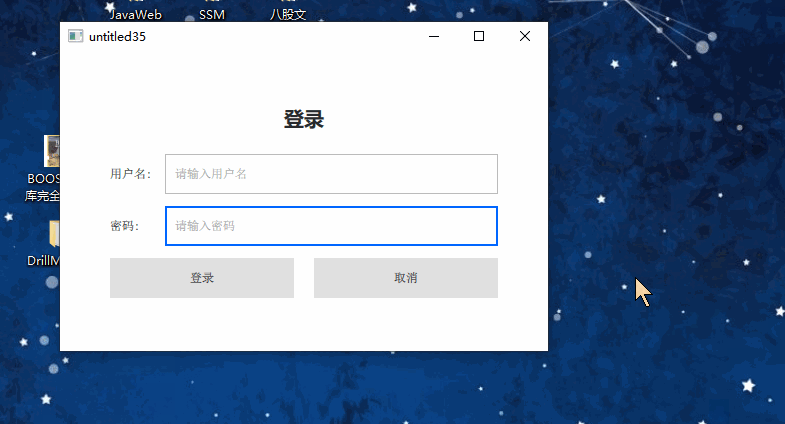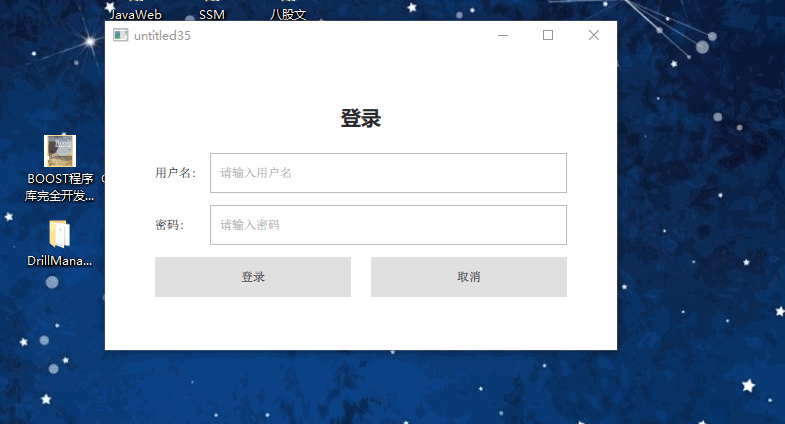
qml写一个自适应登录框
1、前言 写一个可自由伸缩的登录框,,(横向上) 关键:给相关控件赋予 Layout.fillWidth: true 属性 即可。 2、代码 //main.qml import QtQuick 2.12 import QtQuick.Controls 2.12 import QtQml 2.12 import QtQuic…...

考研高数(导数的定义)
总结: 导数的本质就是极限。 函数在某点可导就必连续,连续就有极限且等于该点的函数值。 例题1:(归结原则的条件是函数可导) 例题2: 例题3:...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...
