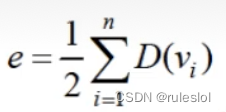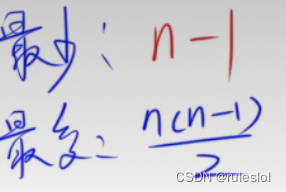软考24-上午题-图1
一、数据结构的回忆
线性结构:(一对一)
除首结点没有前驱、末尾结点没有后继外,一个结点只有唯一的一个直接前驱和唯一的一个直接后继。
树结构:(一对多)
除根节点没有前驱节点外,其余的每个节点只有唯一的一个前驱节点和多个后继结点。
图:(多对多)
任意两个节点之间都可能有直接的关系,图中一个节点的前驱节点和后继结点的数目没有限定。
二、图的定义
图是由集合V和E构成的二元组,记作G=(V, E) 。
V:图中定点的非空有限集合;(数据元素)
E:图中边的有限集合;(数据元素之间的关系)
示例:
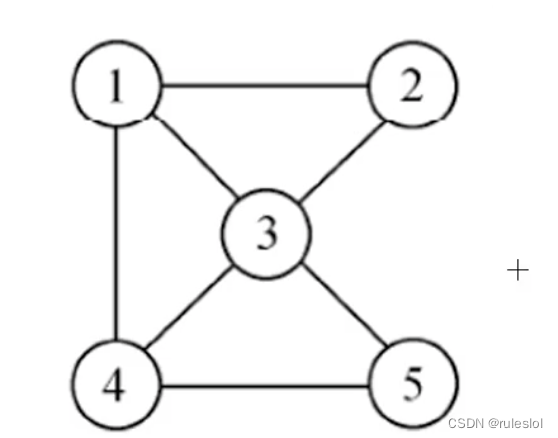
出度(有向图):有某个顶点为起点的边的个数称为该顶点的出度。
入度(无向图):有某个顶点为终点的边的个数称为该顶点的出度。
度(有向图、无向图):入度 + 出度
无向图、有向图:
边数e = 每个顶点的度,相加/2
路径:指图中从一个顶点出发,依次经过若干个顶点到达另一个顶点的一条路线。其中经过的每个顶点在路径中只出现一次;
路径长度:路径上,边、弧的数目;
回路:指从某个顶点出发,经过若干个顶点后回到该顶点的路径。其中经过的每个顶点在路径中只出现一次,除了起点和终点重合的情形。
简单路径:在一个图中从一个顶点到另一个顶点之间没有重复经过任何顶点的路径。简单路径是一条路径,其中顶点没有重复出现。
三、特殊的图
3-1、有向图
图中每条边都是有方向的,顶点之间的关系用<Vi, Vj>表示,它说明从Vi到Vj的一条有向边(也称为弧)。Vi是有向边的起点,称为弧尾;Vj是有向边的终点,称为弧头。
<Vi, Vj>和<Vj, Vi>分别表示两条边。
示例:
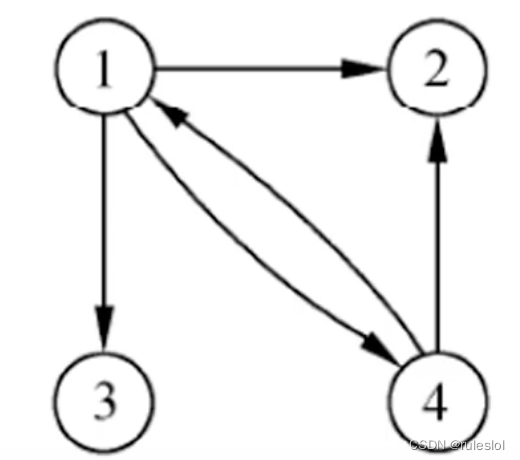
3-1-1、强连通图:
有向图中,每一对顶点Vi,Vj,从顶点 Vi到顶点Vj和从顶点 Vj到顶点Vi都存在路径。
强连通图:n个节点,最少有n条边,最多有n(n-1)条边
3-2、无向图
图中的每条边都是无方向的,顶点Vi和Vj之间的边用(Vi,Vj) 表示。
在无向图中(Vi,Vj) 与(Vj,Vi) 表示的是同条边。
示例:
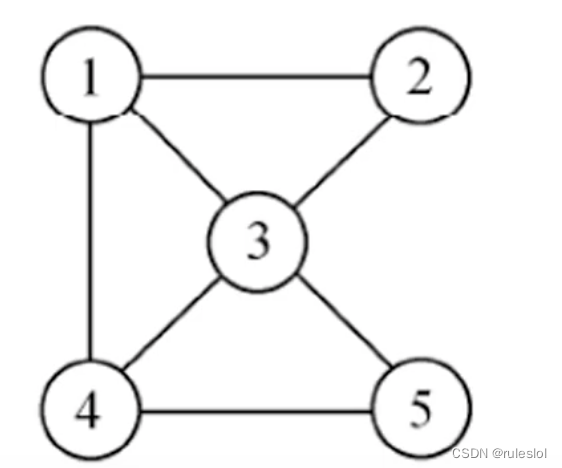
3-2-1、连通图:
无向图中,任意两个顶点都是连通的(任意两个顶点都有路径);
【注意】:
不一定非的是直接路径!!!
例如:顶点1到顶点5,有路径:(v1, v3)、(V3, V5)
无向连通图:n个节点,最少有n-1条边,最多有n(n-1)/2条边
3-3、完全图
一个图中有n个顶点,每个顶点和其他n-1个顶点之间都有边。(直接的边!!!)
完全图的分类:
- 无向完全图
- 有向完全图
含有n个顶点的无向完全图,共有n(n-1)/2条边。
含有n个顶点的有向完全图,共有n(n-1)条边。
四、真题
真题1:D
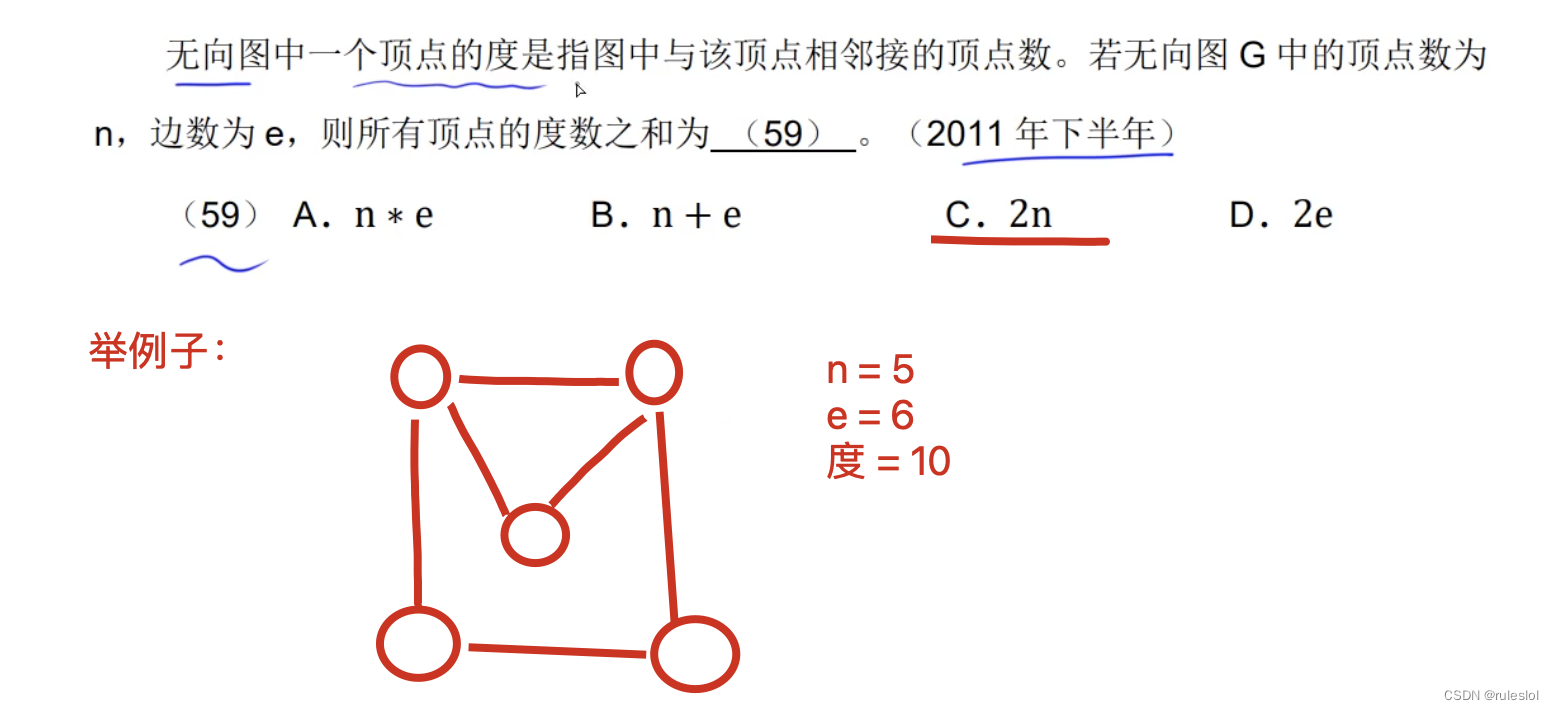
有向图、无向图:边数为e,所有顶点的度数之和为2e
真题2:

相关文章:

软考24-上午题-图1
一、数据结构的回忆 线性结构:(一对一) 除首结点没有前驱、末尾结点没有后继外,一个结点只有唯一的一个直接前驱和唯一的一个直接后继。 树结构:(一对多) 除根节点没有前驱节点外,…...

书生·浦语大模型第四课作业
基础作业: 构建数据集,使用 XTuner 微调 InternLM-Chat-7B 模型, 让模型学习到它是你的智能小助手,效果如下图所示,本作业训练出来的模型的输出需要将不要葱姜蒜大佬替换成自己名字或昵称! 1.安装 # 如果你是在 Int…...

勒索攻击风起云涌,Sodinokibi深度分析
前言 Sodinokibi勒索病毒,又称为REvil勒索病毒,这款勒索病毒最早在国内被发现是2019年4月份,笔者在早期分析这款勒索病毒的时候就发现它与其他勒索病毒不同,于是被笔者称为GandCrab勒索病毒的“接班人”,为什么它是Ga…...
)
1124. 骑马修栅栏(欧拉路径,模板)
农民John每年有很多栅栏要修理。 他总是骑着马穿过每一个栅栏并修复它破损的地方。 John是一个与其他农民一样懒的人。 他讨厌骑马,因此从来不两次经过一个栅栏。 你必须编一个程序,读入栅栏网络的描述,并计算出一条修栅栏的路径…...

C# CAD2016获取数据操作BlockTableRecord、Polyline、DBObject
一、数据操作说明 //DBObject 基础类 DBObject dbObj (DBObject)tr.GetObject(outerId, OpenMode.ForRead); //Polyline 线段类 Polyline outerPolyline (Polyline)tr.GetObject(outerId, OpenMode.ForRead); //BlockTableRecord 块表类 BlockTableRecord modelSpace (Bloc…...
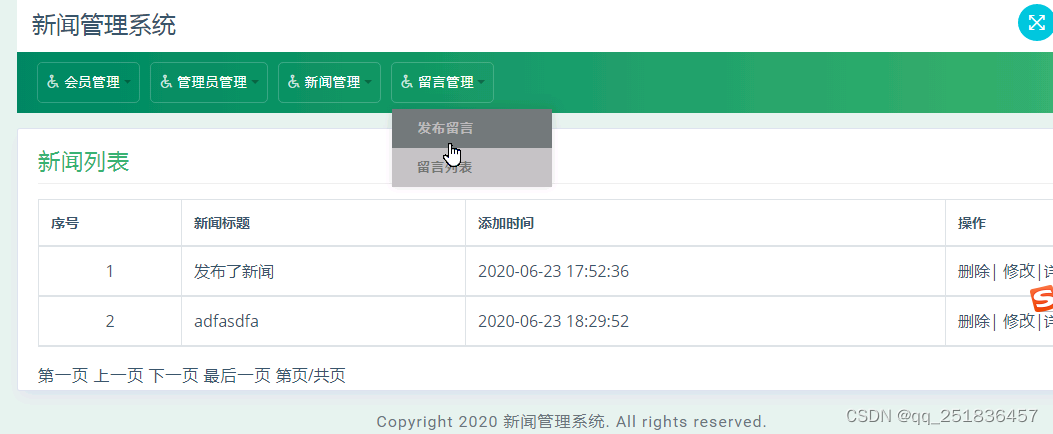
java SSM新闻管理系统myeclipse开发mysql数据库springMVC模式java编程计算机网页设计
一、源码特点 java SSM新闻管理系统是一套完善的web设计系统(系统采用SSM框架进行设计开发,springspringMVCmybatis),对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S…...
Linux_线程
线程与进程 多级页表 线程控制 线程互斥 线程同步 生产者消费者模型 常见概念 下面选取32位系统举例。 一.线程与进程 上图是曾经我们认为进程所占用的资源的集合。 1.1 线程概念 线程是一个执行分支,执行粒度比进程细,调度成本比进程低线程是cpu…...
【selenium】
selenium是一个Web的自动化测试工具,最初是为网站自动化测试而开发的。Selenium可以直接调用浏览器,它支持所有主流的浏览器。其本质是通过驱动浏览器,完成模拟浏览器操作,比如挑战,输入,点击等。 下载与打…...

HX711压力传感器学习一(STM32)
目录 原理图: 引脚介绍: HX711介绍工作原理: 程序讲解: 整套工程: 发送的代码工程,与博客的不一致,如果编译有报错请按照报错和博客进行修改 原理图: 引脚介绍: VCC和GND引…...

作业2.13
1、选择题 1.1、若有定义语句:int a[3][6]; ,按在内存中的存放顺序,a 数组的第10个元素是 D A)a[0][4] B) a[1][3] C)a[0][3] D)a[1][4] 1.2、有数组 int a[5] {10,20,30,40,50},…...

ArcGIS学习(七)图片数据矢量化
ArcGIS学习(七)图片数据矢量化 通过上面几个任务的学习,大家应该已经掌握了ArcGIS的基础操作,并且学习了坐标系和地理数据库这两个非常重要且稍微难一些的专题。从这一任务开始,让我们进入到实战案例板块。 首先进入第一个案例一一图片数据矢量化。 我们在平时的工作学…...

G口大流量服务器选择的关键点有哪些?
G口服务器指的是接入互联网的带宽达到1Gbps以上的服务器,那么选择使用G口大流量服务器的用户需要注意哪些选择 关键点呢?小编为您整理关于G口大流量服务器的关键点。 G口服务器通常被用于需要大带宽支持的业务场景,比如视频流媒体、金融交易平台、电子商…...

MongoDB聚合:$unset
使用$unset阶段可移除文档中的某些字段。从版本4.2开始支持。 语法 移除单个字段,可以直接指定要移除的字段名: { $unset: "<field>" }移除多个字段,可以指定一个要移除字段名的数组: { $unset: [ "<…...

DS Wannabe之5-AM Project: DS 30day int prep day14
Q1. What is Alexnet? Q2. What is VGGNet? Q3. What is VGG16? Q4. What is ResNet? At the ILSVRC 2015, so-called Residual Neural Network (ResNet) by the Kaiming He et al introduced the anovel architecture with “skip connections” and features heavy b…...

【程序设计竞赛】C++与Java的细节优化
必须强调下,以下的任意一种优化,都应该是在本身采用的算法没有任何问题情况下的“锦上添花”,而不是“雪中送炭”。 如果下面的说法存在误导,请专业大佬评论指正 读写优化 C读写优化——解除流绑定 在ACM里,经常出现…...

Java缓冲流——效率提升深度解析
前言 大家好,我是chowley,在我之前的项目中,用到了缓冲流来提高字符流之间的比较速度,缓冲流的主要作用类似于数据库缓存,提高IO操作效率。 缓冲流 在Java的输入输出操作中,缓冲流是提高性能的重要工具之…...
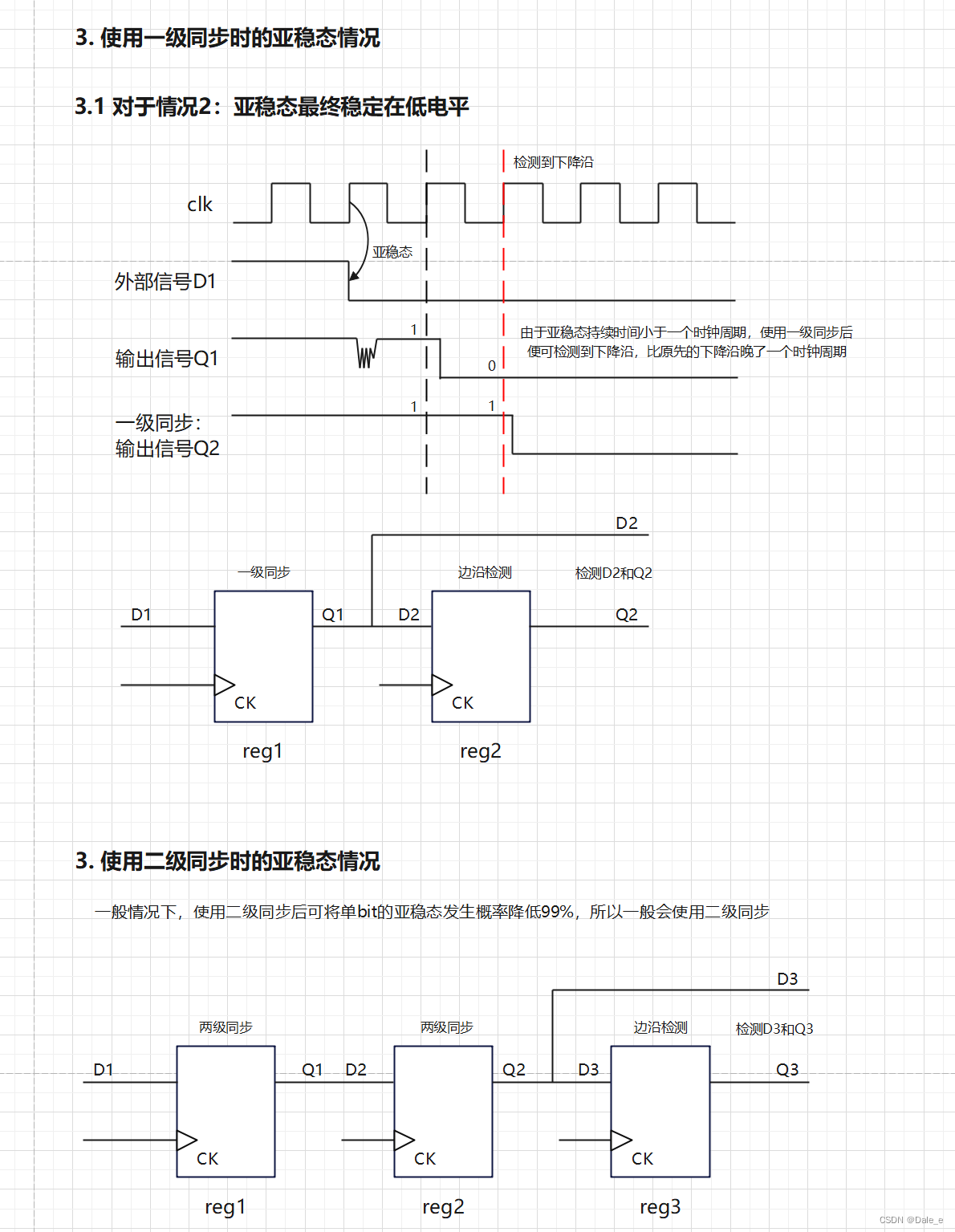
16 亚稳态原理和解决方案
1. 亚稳态原理 亚稳态是指触发器无法在某个规定的时间段内到达一个可以确认的状态。在同步系统中,输入总是与时钟同步,因此寄存器的setup time和hold time是满足的,一般情况下是不会发生亚稳态情况的。在异步信号采集中,由于异步…...
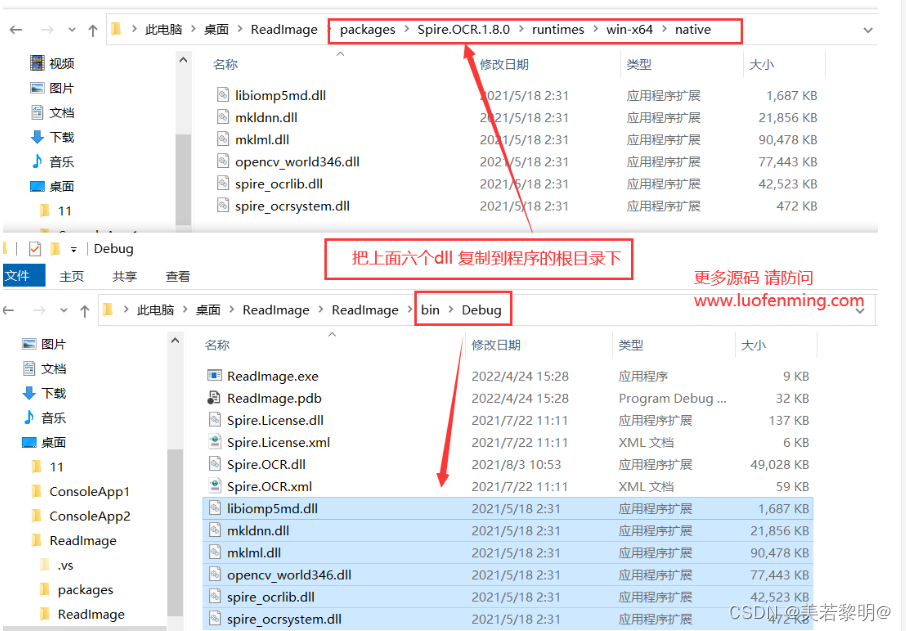
C# OCR识别图片中的文字
1、从NuGet里面安装Spire.OCR 2、安装之后,找到安装路径下,默认生成的packages文件夹,复制该文件夹路径下的 6 个dll文件到程序的根目录 3、调用读取方法 OcrScanner scanner new OcrScanner(); string path "C:\1.png"; scann…...
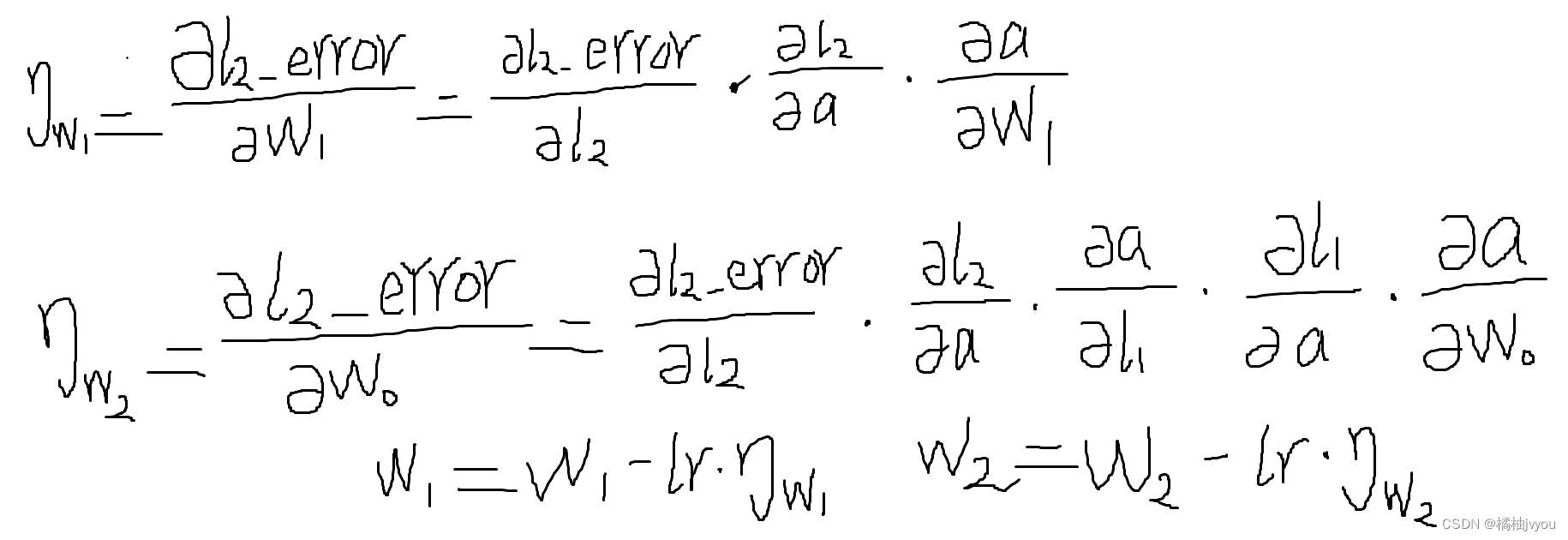
使用python-numpy实现一个简单神经网络
目录 前言 导入numpy并初始化数据和激活函数 初始化学习率和模型参数 迭代更新模型参数(权重) 小彩蛋 前言 这篇文章,小编带大家使用python-numpy实现一个简单的三层神经网络,不使用pytorch等深度学习框架,来理解…...

CSS定位装饰
网页常见布局方式 标准流 块级元素独占一行---垂直布局 行内元素/行内块元素一行显示多个----水平布局 浮动 可以让原本垂直布局的块级元素变成水平布局 定位 可以让元素自由的摆放在网页的任意位置 一般用于盒子之间的层叠情况 使用定位步骤 设置定位方式 属性名&am…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...