力扣题目训练(8)
2024年2月1日力扣题目训练
- 2024年2月1日力扣题目训练
- 404. 左叶子之和
- 405. 数字转换为十六进制数
- 409. 最长回文串
- 116. 填充每个节点的下一个右侧节点指针
- 120. 三角形最小路径和
- 60. 排列序列
2024年2月1日力扣题目训练
2024年2月1日第八天编程训练,今天主要是进行一些题训练,包括简单题3道、中等题2道和困难题1道。惰性太强现在才完成,不过之后我会认真完成的。
404. 左叶子之和
链接: 左叶子之和
难度: 简单
题目:

运行示例:
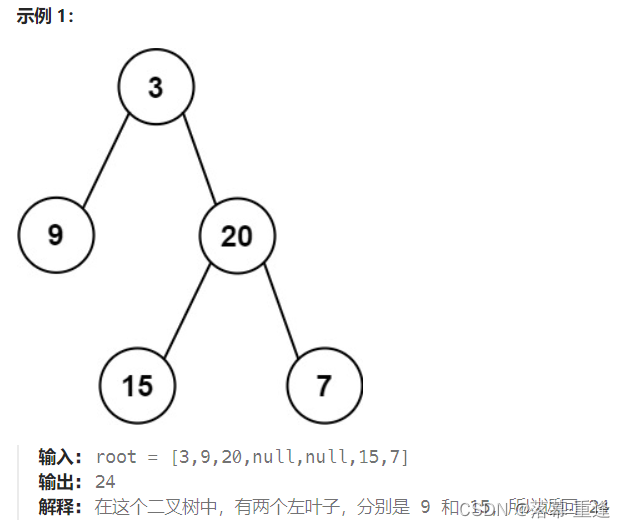
思路:
要求所有左叶子之和也就是通过遍历进行判断。
代码:
class Solution {
public:void preorder(TreeNode* root, int& res){if(root != NULL){if(root->left != NULL && root->left->left == NULL && root->left->right == NULL) res += root->left->val;preorder(root->left,res);preorder(root->right,res);}}int sumOfLeftLeaves(TreeNode* root) {int res = 0; preorder(root, res);return res;}
};
405. 数字转换为十六进制数
链接: 找不同
难度: 简单
题目:

运行示例:

思路:
这道题将给定的整数 转换为十六进制数,负整数使用补码运算方法。
在补码运算中,最高位表示符号位,符号位是 0 表示正整数和零,符号位是 1表示负整数。32位有符号整数的二进制数有 32 位,一位十六进制数对应四位二进制数,因此 32 位有符号整数的十六进制数有 8位。将 num 的二进制数按照四位一组分成 8组,依次将每一组转换为对应的十六进制数,即可得到 num的十六进制数。
假设二进制数的 8组从低位到高位依次是第 0组到第 7组,则对于第 i组,可以通过 (nums>>(4×i)) & 0xf得到该组的值,其取值范围是 0 到 15。
代码:
class Solution {
public:string toHex(int num) {if(num == 0) return "0";string res;for(int i = 7; i >= 0; i--){int val = (num >> (4 * i)) &0xf;if(res.size() > 0 || val > 0){char digit = val < 10 ?(char)('0'+val):(char)('a'+val-10);res += digit;}}return res;}
};
409. 最长回文串
链接: 最长回文串
难度: 简单
题目:

运行示例:

思路:
这道题本质就是计数看字母能不能组成回文数,若为偶数则可以,若为奇数则只有一个能组成,其余的需要减去1变为偶数才能构成回文数。
代码:
class Solution {
public:int longestPalindrome(string s) {bool flag = false;int ans = 0;unordered_map<char,int> temp;for(int i = 0; i < s.size(); i++){temp[s[i]]++;}for (auto p : temp){int value = p.second; if(value % 2 != 0){ans += value-1;if(flag == false){flag = true;ans++;} }else{ans += value;}}return ans;}
};
116. 填充每个节点的下一个右侧节点指针
链接: 填充节点
难度: 中等
题目:
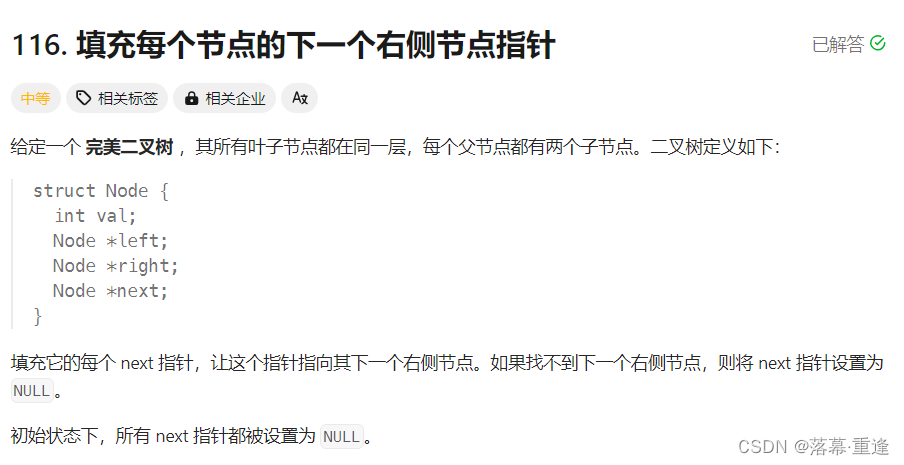
运行示例:
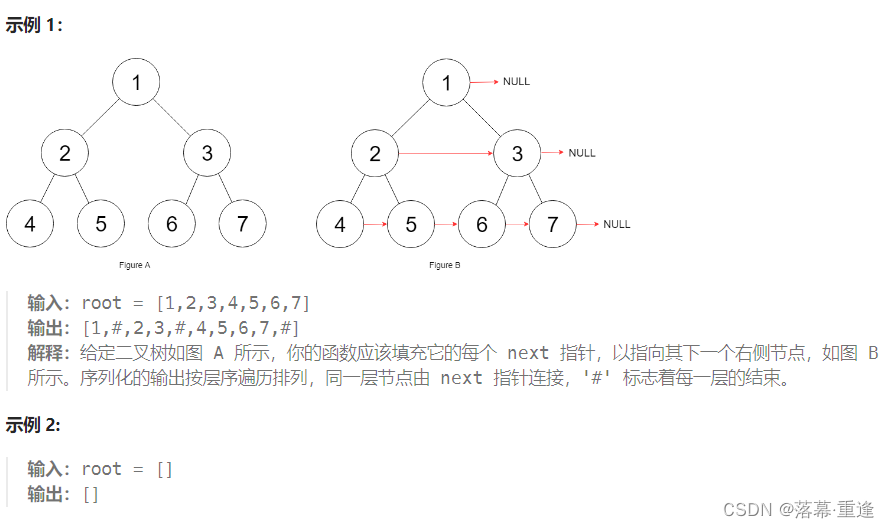
思路:
这道题可以看出是使用层次遍历来完成,故利用队列完成。
代码:
class Solution {
public:Node* connect(Node* root) {if(root == NULL) return NULL;queue<Node*> Q;Q.push(root);while(!Q.empty()){int size = Q.size();for(int i = 0; i < size; i++){Node* curr = Q.front();Q.pop();if(i == size-1){curr->next = NULL;}else{curr->next = Q.front();}if(curr->left != NULL) Q.push(curr->left);if(curr->right != NULL) Q.push(curr->right);}}return root;}
};
120. 三角形最小路径和
链接: 路径和
难度: 中等
题目:

运行示例:

思路:
可以看出这个题是需要利用动态规划解决,f[i][j]=min(f[i−1][j−1],f[i−1][j])+c[i][j]
代码:
class Solution {
public:int minimumTotal(vector<vector<int>>& triangle) {int n = triangle.size();vector<vector<int>> temp(n,vector<int>(n));temp[0][0] = triangle[0][0];for(int i = 1; i < n; i++){temp[i][0] = temp[i-1][0]+triangle[i][0];for(int j = 1; j < i; j++){temp[i][j] = min(temp[i-1][j],temp[i-1][j-1]) + triangle[i][j];}temp[i][i] = temp[i-1][i-1] + triangle[i][i];}return *min_element(temp[n-1].begin(),temp[n-1].end());}
};
60. 排列序列
链接: 排列序列
难度: 困难
题目:

运行示例:

思路:
可以通过观察发现对于 n 个不同的元素(例如数 1,2,⋯ ,n),它们可以组成的排列总数目为 n!。
对于给定的 n 和 k,我们不妨从左往右确定第 k 个排列中的每一个位置上的元素到底是什么。
我们首先确定排列中的首个元素 a1。根据上述的结论,我们可以知道:
以 1为 a1的排列一共有 (n−1)! 个;
以 2为 a1的排列一共有 (n−1)!个;
⋯⋯
以 n 为 a1的排列一共有 (n−1)! 个。
由于我们需要求出从小到大的第 k个排列,因此:
如果 k≤(n−1)!,我们就可以确定排列的首个元素为 1;
如果 (n−1)!<k≤2⋅(n−1)!,我们就可以确定排列的首个元素为 2;
⋯⋯
如果 (n−1)⋅(n−1)!<k≤n⋅(n−1)!,我们就可以确定排列的首个元素为 n。
可以利用这个发现解决问题。
代码:
class Solution {
public:int total(int n){if (n == 0 || n == 1) { return 1; } else { return n * total(n - 1); } }string getPermutation(int n, int k) {string ans = "";vector<int> temp;for(int i = 0; i < n; i++){temp.push_back(i+1);}while(k != 1){int count = (k%total(n-1) == 0)? k/total(n-1) -1:k/total(n-1);int s = temp[count];temp.erase(temp.begin() + count); ans += to_string(s);k -= count* total(n-1);n = n-1;}for(int i =0 ; i < temp.size(); i++){ans += to_string(temp[i]);}return ans;}
};
相关文章:

力扣题目训练(8)
2024年2月1日力扣题目训练 2024年2月1日力扣题目训练404. 左叶子之和405. 数字转换为十六进制数409. 最长回文串116. 填充每个节点的下一个右侧节点指针120. 三角形最小路径和60. 排列序列 2024年2月1日力扣题目训练 2024年2月1日第八天编程训练,今天主要是进行一些…...

理解JAVA EE设计模式
理解JAVA EE设计模式 在Web应用程序的设计和开发阶段,开发人员在开发类似的项目时可能会遇到相似的问题。每名开发人员可能会遇到的问题找出不同或相似的解决方案。但是,这导致一些时间和精力浪费在为相似的问题寻找解决方案上。因此,要啊节省时间和精力,需要记录常见问题…...

GEE:梯度提升树(Gradient Boosting Tree)回归教程(样本点、特征添加、训练、精度、参数优化)
作者:CSDN @ _养乐多_ 对于分类问题,这个输出通常是一个类别标签 ,而对于回归问题,输出通常是一个连续的数值。回归可以应用于多种场景,包括预测土壤PH值、土壤有机碳、土壤水分、碳密度、生物量、气温、海冰厚度、不透水面积百分比、植被覆盖度等。 本文将介绍在Google…...

k8s-资源限制与监控 15
资源限制 上传实验所需镜像 Kubernetes采用request和limit两种限制类型来对资源进行分配。 request(资源需求):即运行Pod的节点必须满足运行Pod的最基本需求才能 运行Pod。 limit(资源限额):即运行Pod期间,可能内存使用量会增加࿰…...

【Ubuntu】在.bashrc文件中误设置环境变量补救方法
这里是vim也不在PATH中了,因为 解决方法就是在输入vim之后提示的vim路径下用vim打开该文件,然后改回来...
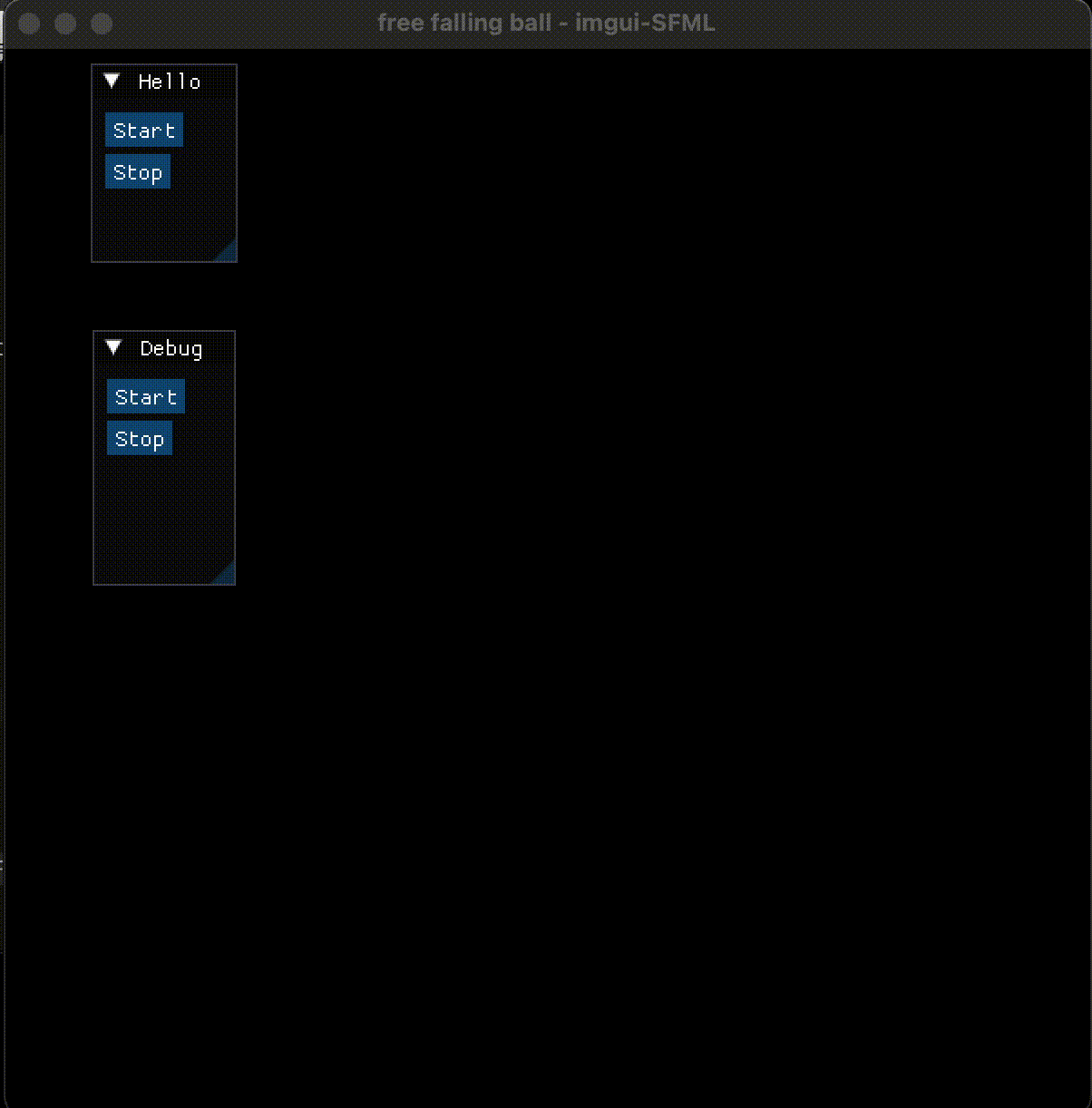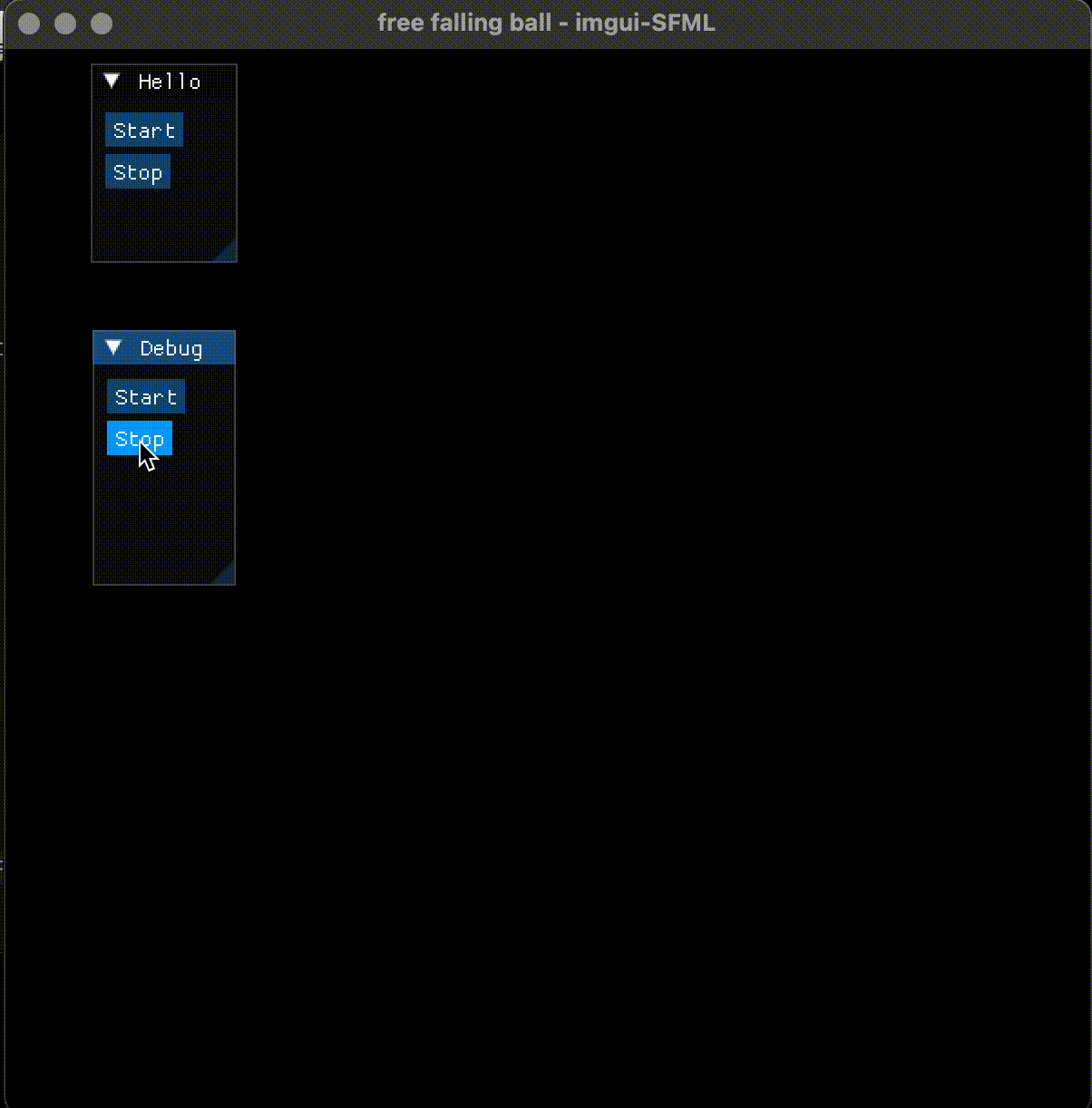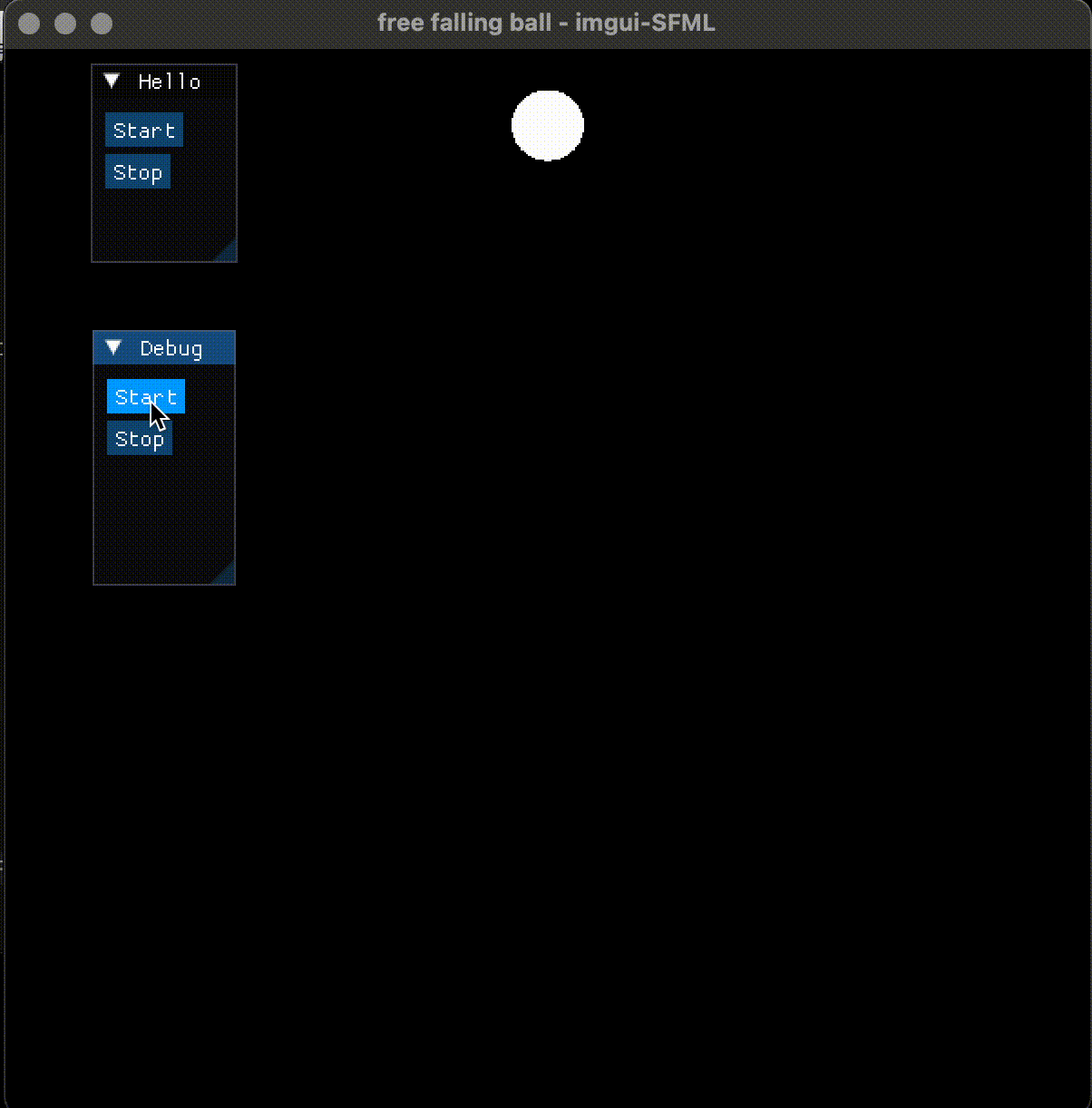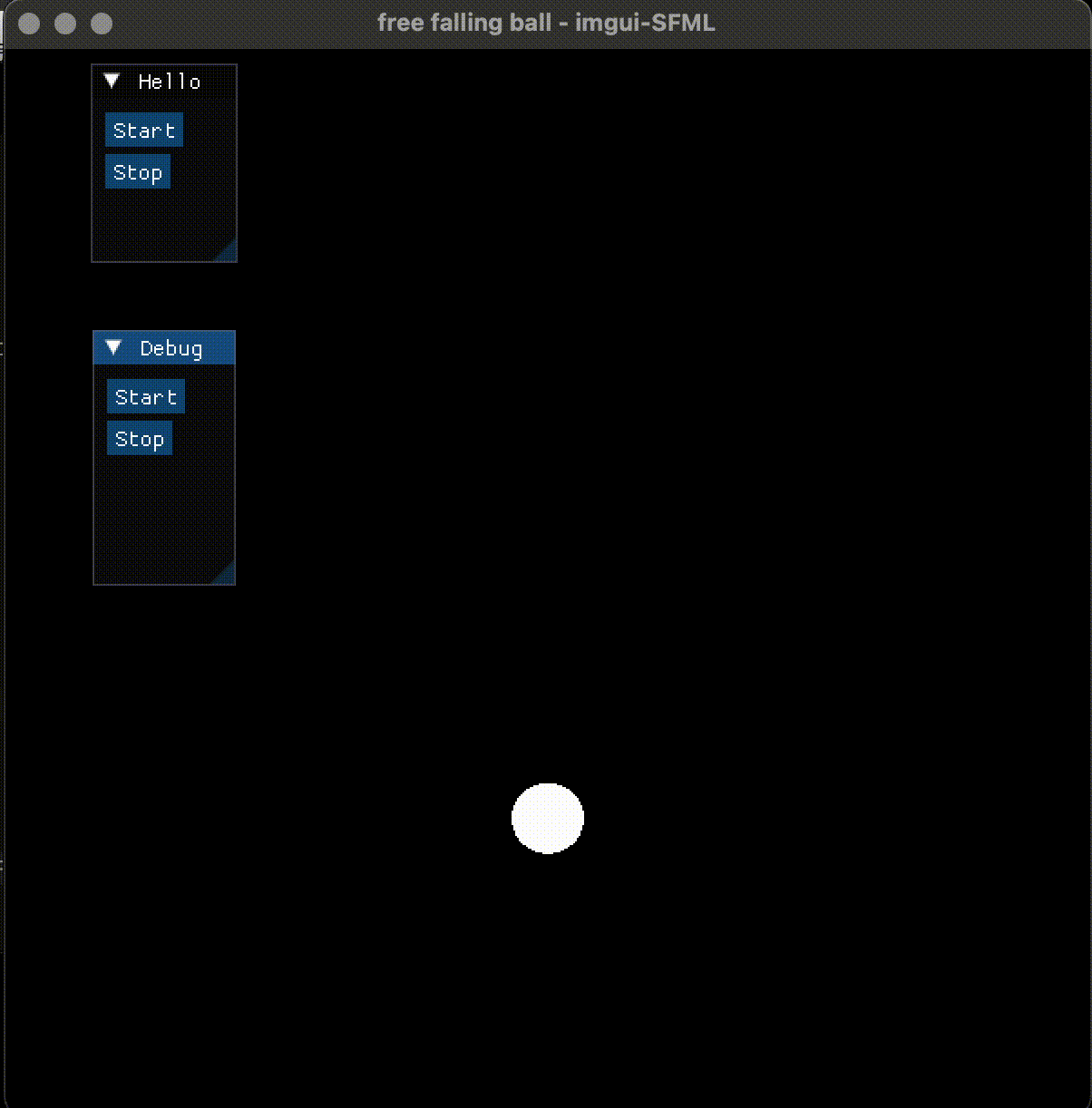
Imgui(1) | 基于imgui-SFML改进自由落体小球
Imgui(1) | 基于imgui-SFML改进自由落体小球 0. 简介 使用 SFML 做2D图形渲染的同时,还想添加一个按钮之类的 GUI Widget, 需要用 Dear Imgui。由于 Imgui 对于2D图形渲染并没有提供类似 SFML 的 API, 结合它们两个使用是一个比较好的方法, 找到了 imgui-SFML 这个…...

Linux-Vim的使用,快速入门Vim,Linux入门教程,精讲Linux
Vim的三种模式 输入模式,键入 i 或 a 或 o 都可以进入输入模式。 普通模式,打开Vim默认的模式。 命令模式,键入 : 进入命令模式。 注意:按下 ESC 可以从输入模式或命令模式退回到普通模式 退出 vim ,需要在普通模式下…...

目标检测 | 卷积神经网络(CNN)详细介绍及其原理详解
前言:Hello大家好,我是小哥谈。卷积神经网络(Convolutional Neural Network,CNN)是一种深度学习模型,主要用于图像识别和计算机视觉任务。它的设计灵感来自于生物学中视觉皮层的工作原理。CNN的核心思想是通…...
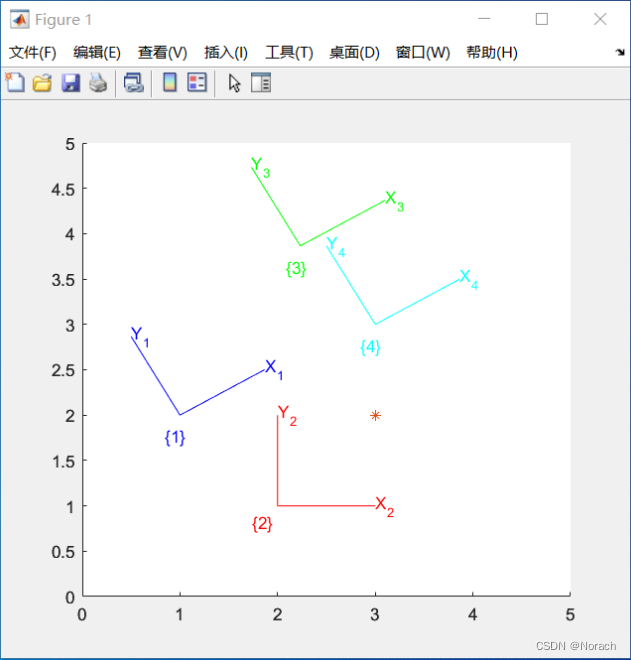
机器人学、机器视觉与控制 上机笔记(第一版译文版 2.1章节)
机器人学、机器视觉与控制 上机笔记(第一版译文版 2.1章节) 1、前言2、本篇内容3、代码记录3.1、新建se23.2、生成坐标系3.3、将T1表示的变换绘制3.4、完整绘制代码3.5、获取点*在坐标系1下的表示3.6、相对坐标获取完整代码 4、结语 1、前言 工作需要&a…...

关于vue2+antd 信息发布后台不足的地方
有的写法可以cv 1.序号递增 {title: "序号",customRender: (text, record, index) > ${index 1},align: "center",}, 2.关于类型 {title: "类型",dataIndex: "type",align: "center",customRender: function (t) {sw…...

Ubuntu+Anaconda 常用指令记录
Anaconda 使用指令记录 1 创建环境 conda create -n name pythonx.x(python版本自己指定)例如 conda create --name myenv: 创建名为"myenv"的新环境。 conda activate myenv: 激活名为"myenv"的环境。 conda deactivate: 退出当前环境。 2 删除环境 c…...

P5732 【深基5.习7】杨辉三角 python解法
# 【深基5.习7】杨辉三角 ## 题目描述 给出 n<20,输出杨辉三角的前 n 行。 如果你不知道什么是杨辉三角,可以观察样例找找规律。 ## 输入格式 ## 输出格式 ## 样例 #1 ### 样例输入 #1 6 ### 样例输出 #1 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5…...

VitePress-12-markdown中使用vue的语法
前言 VitePress 中,markdown文档最终都会转换成为 html文件,我们在访问的时候,也是直接访问的 xxx.html 文件。而且,markdown文档会被作为 [vue单文件] 进行处理,因此,我们我们可以在文档中使用 vue 语法&…...
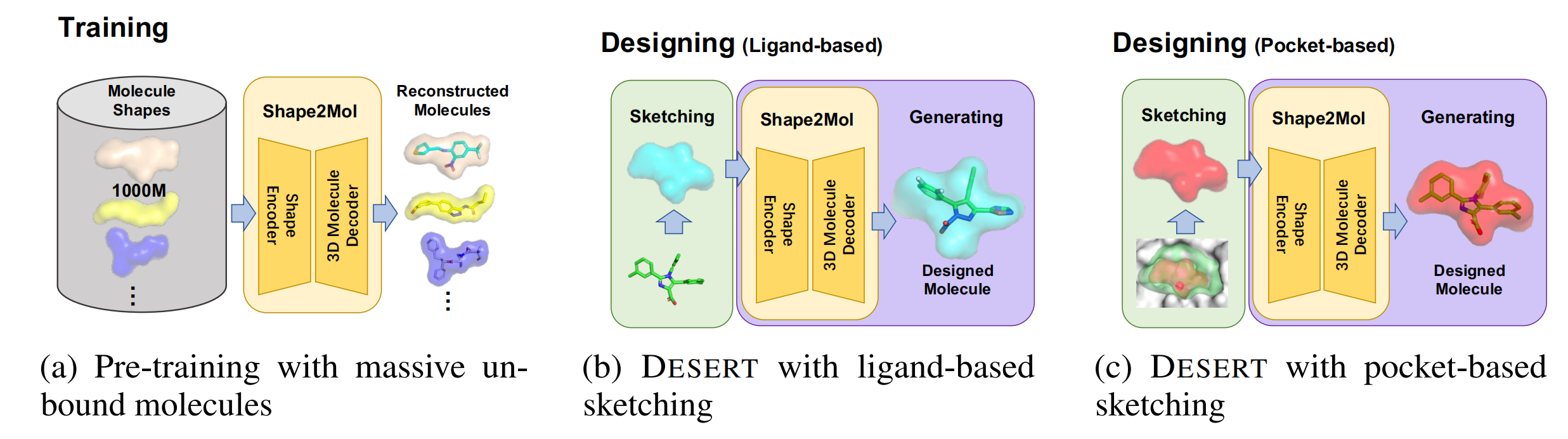
“bound drug/molecule”or “unbound drug/molecule”、molecule shape、sketching是什么?
“bound drug/molecule”or “unbound drug/molecule” For clarity, the following terms will be used throughout this study: “bound drug/molecule” (or “unbound drug/molecule”) refers to the drug/molecule that is bound (or unbound) to proteins [48]. 意思就是…...

深入理解C语言中的函数指针:概念、机制及实战应用
在C语言的世界里,函数是一等公民,可以被赋值给变量,这种特殊的变量就是我们今天要探讨的主角——函数指针。函数指针作为C语言中一种强大的工具,允许我们以间接方式调用函数,从而实现动态绑定、回调函数、策略模式等多…...

《UE5_C++多人TPS完整教程》学习笔记1 ——《P2 关于本课程(About This Course)》
本文为B站系列教学视频 《UE5_C多人TPS完整教程》 —— 《P2 关于本课程(About This Course)》 的学习笔记,该系列教学视频为 Udemy 课程 《Unreal Engine 5 C Multiplayer Shooter》 的中文字幕翻译版,UP主(也是译者&…...

权限系统设计
权限系统设计 RBAC 基于角色的访问控制 ABAC 基于属性的访问控制 普通的系统无非 CRUD,那系统如何控制一个用户该看到哪些数据、能操作哪些功能?日常开发中最常用到 RBAC 和 OAuth2 这两种访问控制和授权方案 RBAC 基于角色的访问控制 所有的访问控制模…...

Ubuntu Desktop - Screenshot (截图工具)
Ubuntu Desktop - Screenshot [截图工具] 1. Search your computer -> Screenshot -> Lock to Launcher2. gnome-screenshot3. System Settings -> Keyboard -> ShortcutsReferences 1. Search your computer -> Screenshot -> Lock to Launcher 2. gnome-s…...
docker 1:介绍
docker 1:介绍 docker解决哪些问题: 传统APP在安装到不同电脑的时候可能会遇到依赖问题,比如缺少VS 20xx,软件无法运行”的情况。docker使用容器技术将软件 依赖打包为image包发布,解决了依赖问题。docker有一个官…...

RibbonBar RibbonPage切换事件
在开发的过程中,我们会用到点击切换page,来响应对应的事件,例如以下事件: 头文件中: void ribboncurrentPageIndexChanged(int index); 实现文件中: connect(ribbonBar(), SIGNAL(currentPageIndexChang…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

Django RBAC项目后端实战 - 03 DRF权限控制实现
项目背景 在上一篇文章中,我们完成了JWT认证系统的集成。本篇文章将实现基于Redis的RBAC权限控制系统,为系统提供细粒度的权限控制。 开发目标 实现基于Redis的权限缓存机制开发DRF权限控制类实现权限管理API配置权限白名单 前置配置 在开始开发权限…...
)
41道Django高频题整理(附答案背诵版)
解释一下 Django 和 Tornado 的关系? Django和Tornado都是Python的web框架,但它们的设计哲学和应用场景有所不同。 Django是一个高级的Python Web框架,鼓励快速开发和干净、实用的设计。它遵循MVC设计,并强调代码复用。Django有…...
